Применение W-модификации метода Годунова при моделировании газодинамических течений в неустойчивой атмосфере

Работа посвящена исследованию закономерностей газодинамического течения, возникающего в покоящейся перегретой атмосфере при погружении в нее компактного облака пыли. Предполагается, что в начальный момент облако пыли покоится, располагается в районе границы тропосферы (высоты 6-14 км) и имеет отрицательную плавучесть, то есть плотность запыленного воздушного облака больше плотности окружающего воздуха. При погружении облака под действием силы тяжести изменяются параметры среды (плотность, давление и др.) как внутри облака, так и в окружающем ее воздухе. В данной работе рассматривается диапазон исходных данных, для которых уплотнение среды облака происходит быстрее, чем окружающего воздуха, в результате чего процесс погружения облака происходит с ускорением (прогрессирующее погружение).

В данной работе используется модификация метода Годунова с вычислением поправок на переменном шаблоне. Основная идея подобных схем заключается в консервативной поправке потоков через границы ячеек для линейной схемы первого порядка [3; 8; 9; 11]. Нелинейный характер поправок, а также переменный шаблон их вычисления позволяют обойти известную теорему Годунова [5] и совместить второй порядок точности схемы с монотонностью.

Пусть гиперболическая система уравнений записана в дивергентном виде:

w, + F(wX + G(w)v = h(w), где w(x, у, t) - вектор из т компонент, F(w), G(w), h(w) - вектор-функции потоков и источниковых членов. Тогда метод Годунова 1-го порядка [6], примененный к модифицированному уравнению

w, + F(w + a)v + G(w + рХ = h(w), даст приближенное решение исходного уравнения со вторым порядком точности по пространству и времени, если

a = ysign(Fw)wv+y w,,

P=ySign(Gw)w, + yW,;

где Fw, Gw- матрицы производных.

В последних формулах производные по времени w, можно заменить на пространственные производные с помощью исходного уравнения:

« = у sign(Fw)wx -у F(w), -yG(wX +yh(wX P = ysign(Gw)wy -yF(wX -yG(wX+yh(w)

Аппроксимация величин аир при численном решении осуществлялась нелинейным образом на W-шаблоне, ориентация которого зависит от направления скорости потока (собственных чисел матриц Fw и Gw) [3].

• § 1.    Постановка задачи и основные уравнения

Атмосфера под действием гравитации имеет неоднородное распределение давления и плотности по высоте. В начальный момент однородное облако запыленного газа диаметра d размещается в атмосфере на некоторой высоте Н и имеет нулевую скорость (рис. 1). Предполагается, что плотность среды облака больше плотности окружающего воздуха. Под действием силы тяжести оно начинает двигаться вниз и деформироваться.

Рис. 1. Начальная конфигурация задачи о погружении облака

Воздух атмосферы рассматриваем как совершенный газ с постоянными теплоемкостями (показатель адиабаты у„=1,4). Предполагаем, что частицы пыли в облаке имеют очень маленький размер, так что движение запыленного газа (воздух плюс пылинки) моделируем в односкоростном приближении. В дополнение к этому предполагаем температурное равновесие между частицами пыли и воздухом. В этом приближении для запыленного газа также применима модель совершенного газа, но с эффективным показателем адиабаты у. зависящем от концентрации пыли. При отсутствии диффузии и химических реакций концентрация, а вместе с тем и эффективное у, описываются обычным уравнением переноса.

С учетом высказанных допущений нестационарные уравнения движения облака и окружающего воздуха выглядят следующим образом:

^ + p.Vy=0;

at

^ + div(x^) = 0;

• —+ (y.V> + lv/> = F;

St           p

—+ div[(e + p)p]= pV • v, at

> где p — давление среды; p - суммарная плотность воздуха и пыли; V - вектор скорости; e = /?/(/-l)+0,5/w2 - полная энергия единицы объема среды, F - вектор внешних сил. Система (1) представляет собой замкнутую систему дифференциальных уравнений относительно искомых функций у, р, р и У .

Для определения таких величин как температура смеси или плотность пыли необходимо указать связь с теплоемкостями воздуха и материала частиц. При нулевой концентрации пыли показатель адиабаты облака совпадает с показателем адиабаты воздуха, то есть у_с1 = у_в = 1,4. Для смеси совершенных газов эффективный показатель адиабаты газа связан с теплоемкостями и плотностями следующим образом:

Р1Ср1 +Р2Ср2

P|^Cvl ⁺ Pl^Cv2

Пыль представляет собой среду без давления, для которой теплоемкость с_р3 = c_v2 = с*. Обозначим р, пространственную плотность пыли, р_б - плотность воздуха в облаке, у_г/ -показатель адиабаты газопылевой смеси в облаке в начальный момент, тогда для теплоемкости смеси в облаке имеем

PSp+Ps^

PA^Psc ’ или с учетом у„ = cjcv р, с‘ у«+—-

Ун =

Рк Cv

1 + ^- то есть показатель адиабаты облака определяется степенью его запыленности и свойствами твердого вещества. Из выражения (2) видно, что наличие пыли приводит к уменьшению показателя адиабаты. Одно и то же значение уг/ может обеспечиваться различной степенью запыленности в зависимости от теплоемкости материала частиц. Так, например, для случая с* = 1,5с„, что приблизительно соответствует силикатным частицам пыли, количественные соотношения между ^d и его запыленностью следующие:

Г^М => — = 2;

Рв

^,=1,05 => — «4,67;

Р«

Y_d=W => — «12,67.

А

Заметим, что рк внутри и вне облака могут отличаться из-за разности температур. Учитывая, что плотность материала частиц более чем на три порядка превосходит ри, получаем, что объемная концентрация пыли не превосходит 1 % и модель запыленного газа применима.

В численном моделировании использовалась дивергентная форма уравнений. Предполагалось, что сила тяжести направлена вертикально вниз, поверхность земли строго горизонтальна и течение является осесимметричным относительно вертикальной оси Oz. Тогда в цилиндрической системе координат дивергентная форма уравнений (1) будет иметь вид:

зи sf(u) ас(и) т*         +          —     -г    , 5< dr      дг V ури уру ури f 0 р рм pv 1 ри 0 (3) и = ри , F= ри2 + р , G = puv , R.= — Г ри2 , r2 = 0 9 ру рии ру2 + р рИУ -pg W Ае + Р^> Ц^ +W XVе ^рК k-pvg) где U - вектор консервативных переменных. Источниковые члены в правой части представляют собой сумму двух векторов. R, учитывает осесимметрию, a R2 - гравитацию.

При переходе к безразмерным величинам за единицу плотности и скорости принимались плотность р0 и скорость звука на поверхности Земли в момент / - 0. За единицу длины принималось 10 км, единицей времени является отношение единицы длины к единице скорости, что составляет примерно 30 с.

• § 2.    Задание начального состояния атмосферы

Рассмотрим вопрос начального распределения параметров атмосферы. Существует несколько простых подходов для задания этого распределения.

Один из них - задание политропной атмосферы [1]. В данном случае имеет место соотношение р = const -р", где н - показатель политропы. При п = у уравнение превращается в адиабатический закон, при п = 1 - атмосфера с однородной температурой статического равновесия. Из (1) с Р = О вытекают начальные распределения давления и плотности:

Р = Ро 1-

^^gz я Ро

Р = Ро 1-

и-1 Ро

И Ро

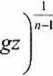
Здесь />₀ и р₀ - это давление и плотность на поверхности Земли. С учетом уравнения состояния р = pRT получаем линейное распределение температуры атмосферы T’(z) по высоте. При л = 1,4 уменьшение температуры с высотой составляет примерно 10°К/км. На высоте h = ——^- падает до нуля, то есть политропная атмосфера имеет конечную высоту, «-1Ро^

что является плохим приближением к реальности.

Другой подход - задание распределения температуры по высоте с использованием тех или иных теоретических и экспериментальных измерений. Атмосферные процессы, влияющие на характер распределения температуры по высоте, очень сложны и достаточно подробно изложены в монографии [4]. Там приводится профиль температуры в условиях радиационного равновесия (при отсутствии конвекции и водяного пара), который изображен на рисунке 2 сплошной линией. Конвекция возбуждается тогда, когда градиент температуры превосходит некоторое критическое значение. В первом приближении оно равно примерно 10°К/км, что соответствует показателю политропы л =1,4 [7]. Атмосфера в данном случае радиационного равновесия является неустойчивой, однако она может существовать в таком режиме некоторое время, так как для возбуждения и развития конвекции требуется внешнее возмущение и время.

В атмосфере всегда присутствуют локальные конвективные движения, которые стремятся привести атмосферу в устойчивое состояние. Распределение температуры в результате такого конвективного приспособления для реальной атмосферы изображено на рисунке 2 штриховой линией. Оно соответствует более низким градиентам 6,5 ° К/км, по сравнению с адиабатическим равновесием.

Интегрирование уравнения статики позволяет получить распределение давления р^) по высоте по заданному распределению температуры T(z):

Р^ Ров

г Kdz "\RT^

где р0 — давление на поверхности земли; g — ускорение силы тяжести; R — газовая постоянная. Тогда, зная температуру, находим давление, а затем плотность. Можно ввести dp    dp        „ локальный показатель политропы из условия — = п—, который удобно использовать для Р    Р оценки локальной устойчивости.

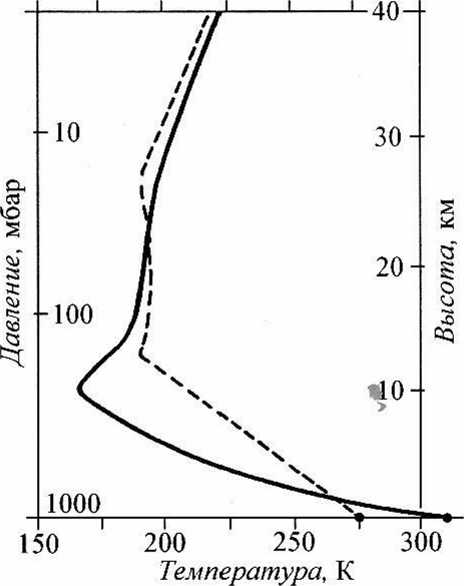
Рис. 2. Профили средней температуры в случае радиационного равновесия (сплошная линия) и при конвективном приспособлении к постоянному вертикальному градиенту температуры (штриховая линия)

На рисунке 3 изображены графики локального показателя политропы атмосферы для случая радиационного равновесия и для среднего арифметического распределений, соответствующих кривым на рисунке 2. Единица длины по оси г соответствует 10 км.

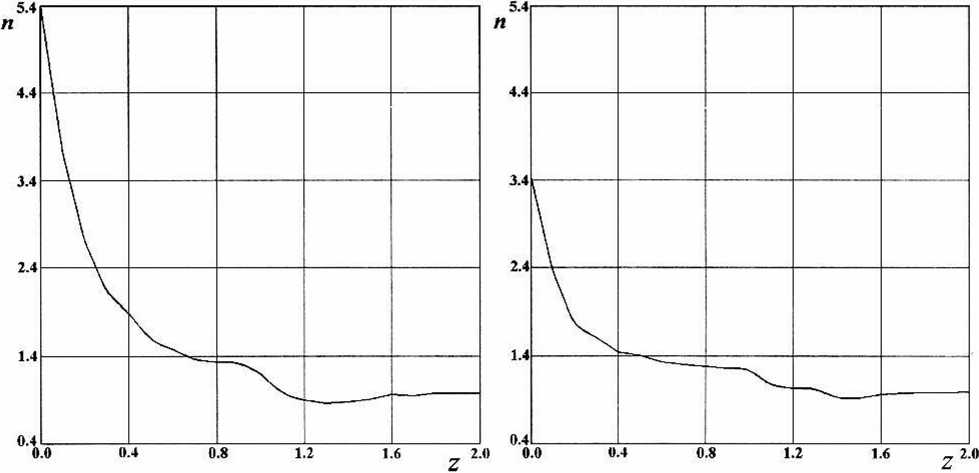
Рис. 3. Зависимости локальных показателей политропы от высоты для двух распределений температур, которые использовались в расчетах

В первом случае слои атмосферы, находящиеся на высоте более 8 км, будут устойчивыми (п < 1,4). Во втором - атмосфера будет неустойчивой до высоты 5 км.

• § 3.    Особенности численного метода

Численное решение уравнений осуществлялось с помощью W-модификации схемы Годунова, которая была обобщена на случай смеси двух совершенных газов с переменным показателем адиабаты у.

Перепишем первое уравнение из (3) в виде

8 , \ 8 z \ 8 z \ ар»

В качестве граничных условий на правой вертикальной границе ставились условия симметрии. Нижняя горизонтальная граница является поверхностью Земли. Для нее обычные классические условия нелротекания не совсем годятся. Нужно учитывать существующий градиент давления таким образом, чтобы поток массы, импульса и энергии через горизонтальную поверхность был равен нулю. В этом случае задавались фиксированные градиенты давления и плотности, полученные из начальных условий. Аналогично нужно учитывать наличие градиента давления на верхней границе сетки.

Свободная граница при длительных расчетах для дозвуковых течений может генерировать флуктуации. Для их погашения на левой вертикальной границе был добавлен демпферный слой из нескольких десятков ячеек с увеличивающимся шагом, где расчет проводился по обычной схеме. Однако это позволило отодвинуть границу так, чтобы ее влияние на ту расчетную область, где исследуется течение, было минимальным.

• § 4.    Результаты численного эксперимента

Расчеты проводились для следующего диапазона исходных параметров:

Диаметр облака d = 0,2 .

Начальное положение облака Н - 0,6; 0,9; 1,4.

Показатель адиабаты газопылевой смеси облака у_с1 = 1,02; 1,05; 1,1.

Отношение плотности облака к плотности окружающей атмосферы pjp„ =1,05; 1,1; 1,2; 1,3; 1,4; 1,5.

В расчетах бралось распределение температуры, показанное на рисунке 2 сплошной линией, и распределение, полученное как среднее арифметическое распределений, соответствующих сплошной и штриховой линиям.

Расчетная область составляла 2 единицы по радиусу и высоте (то есть 20 км х 20 км) и покрывалась квадратной сеткой (Ar = Az) размером 1 000 х 1 000 ячеек.

На рисунке 4 изображены изолинии поля плотности на различные моменты времени погружения облака для варианта //=0,9; ^_г/ = 1,05 ; p_cJ р_п = 1,1 ■ В начальный момент времени облако покоится. Под действием силы тяжести оно начинает погружаться и деформироваться (рис. 4»), К моменту взаимодействия с землей облако принимает характерную тороидально-слоистую вихревую структуру (рис. 46).

Рис. 4. Изолинии плотности течения в различные моменты времени при погружении газопылевого облака для случая Н = 0,9 ; у а = 1,05 ; Ра) Ра = 1,1 •

Дискретность изолиний Ар = 0,025

Г = 12

После столкновения с поверхностью образуется небольшой, но интенсивный вихрь, распространяющийся по поверхности земли в сторону от эпицентра падения. Он хорошо виден на рисунке 4е. Вслед за ним возникает несколько менее интенсивных вихрей (рис. 4г-е). Около эпицентра падения с течением времени образуется большая всплывающая струя (рис. 4д-е). Динамику образования этой струи можно проследить на рисунке 5, где изображено векторное поле скоростей и изолинии температуры воздуха в области формирования восходящей струи.

На рисунке 5а хорошо прослеживается, что падающее запыленное облако увлекает вслед за собой воздух атмосферы. Это видно как по полю скоростей, так и по температуре, которая имеет пониженное значение над эпицентром падения (цифра I на рис. 5а\ На этом же фрагменте также видно, что упавшее облако растекается по плоскости, и вытесняемый им воздух устремляется к оси симметрии. На рисунке 56 наблюдается начальная фаза нарушения устойчивости и возбуждения конвекции. Стекающийся к оси симметрии воздух изменяет направление и начинает подниматься вверх. При этом формируется upoi иб в профиле распределения температуры (цифра 2 на рис. 56). Теплый воздух начинает подниматься, в то время как холодный воздух на оси симметрии опускается (цифра 1). Этот процесс лавинообразно нарастает. На рисунке 5в изображена уже достаточно развитая его фаза. Наблюдается своеобразная воронка, по краям которой теплый воздух поднимается вверх (цифра 2), а в центре холодный воздух опускается вниз (цифра 1) и растекается по плоскости. На плоскости образуется тонкий слой растекающегося экмановского потока [2], выше которого направление движения масс воздуха прямо противоположное, то есть к центру.

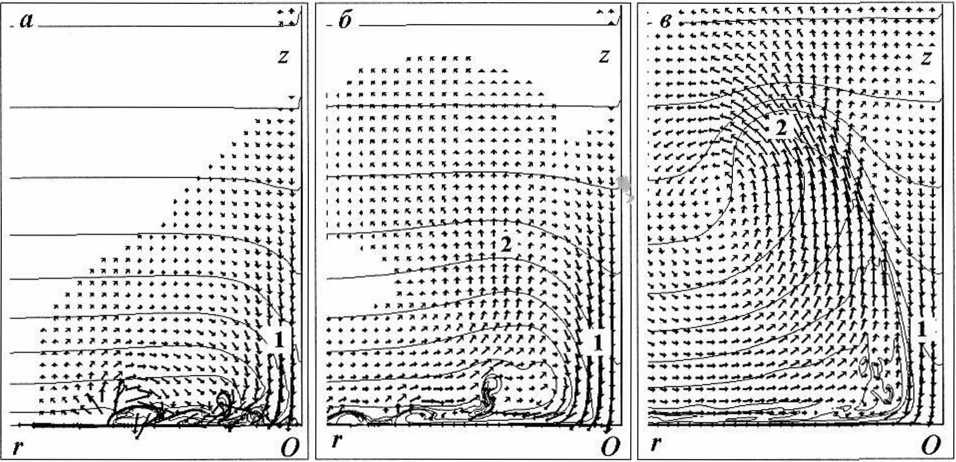
Рис. 5. Возникновение вертикальной конвекции. Изображены изолинии температуры и поле скорости воздуха в атмосфере в три последовательных момента времени

Восходящий поток будет ускоряться, пока не достигнет устойчивых слоев атмосферы. Затем он замедляется, и происходит растекание потока в стороны. При достаточной скорости восходящего потока всплывающее облако может проникнуть и в устойчивые слои атмосферы.

Следующий вариант расчетов относится к случаю средней запыленности ( y_d = 1,05) с начальной относительной плотностью запыленного облака (о = p_cJp_a ) ст = 1,5 . На рисунке б для сравнения приведены изолинии плотности для вариантов ст = 1,1 (слева) и ст = 1,5 (справа). Различие величины а при фиксированном у_с/ связано с различным значением начальной температуры облака. В данном случае упомянутые варианты соответствуют Т, — 880 ° К и Т, = 650 ° К (при условии, что температура на поверхности земли Т_о = 300 ° К).

Из сравнения результатов видно, что более плотное и холодное облако опускается гораздо быстрее, при этом раньше начинает формироваться восходящая струя, хотя заключительная стадия формирования воронки в обоих случая происходит приблизительно одновременно. Даже сверх того, в первом случае более легкого облака, несмотря на задержку, интенсивность конвекции в верхних слоях атмосферы в заключительной стадии больше.

В обоих этих вариантах возникает одиночный вихрь, убегающий от эпицентра вдоль горизонтальной поверхности. Для первого варианта он наблюдался в диапазоне времени 10 <  t < 1 б, а для второго - в диапазоне 5 < / < 10 .

/ = 8

г = 16

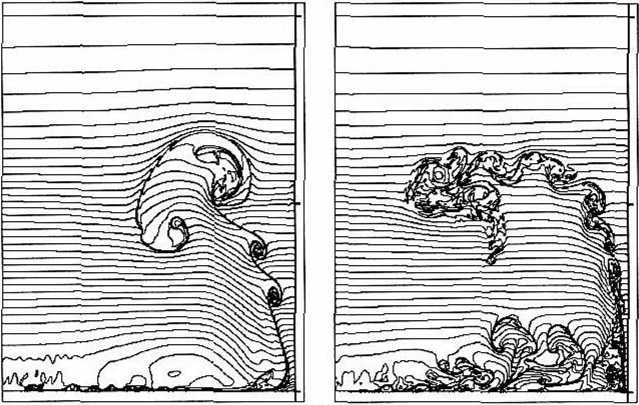
/ = 24

Рис. 6. Изолинии плотности течения на различные моменты времени при погружении газопылевого облака в случае Н = 0,9 , у_d = 1,05 для различных начальных плотностей облака: p_rJ р„ =1,1 (слева) и р Jp_u =1,5 (справа)

Отметим основные закономерности, в той или иной степени присутствующие в большинстве вариантов расчетов. Главным отличительным моментом при погружении облака большой запыленности (с малым показателем адиабаты) является формирование второго убегающего вихря. При падении облака из более низкого начального положения (Я = 0,6; то есть размерное значение 6 км) в целом наблюдается картина, в общем схожая со случаем Н = 0,9 . Успевает сформироваться вихрь, а в случае малого ^_с, наблюдается каскад из двух вихрей, которые распространяются по поверхности земли приблизительно с одинаковой скоростью. При падении облака с высоты более 10 км при малой начальной плотности облака устойчивые слои атмосферы препятствуют его погружению. Пыль не достигает поверхности земли, а совершает колебательные движения на больших высотах. В случае большой начальной плотности характер погружения гораздо сложнее. Более плотное облако способно проникнуть в область неустойчивой атмосферы, где происходит его ускорение. При преодолении этого порога оно теряет часть своей массы, облако разваливается, что приводит к формированию нескольких, но менее интенсивных вихрей.

Подводя итог анализу численных расчетов, отметим основные закономерности течения, которые возникают при падении запыленного облака. Во всех случаях, когда облако достигает поверхности земли, образуется вихрь, а при большой запыленности два последовательных вихря, убегающие от эпицентра с высокой скоростью. Главным откликом неустойчивой атмосферы является формирование конвективной воронки, которая образуется через некоторое время непосредственно после падения облака. Внутри этой воронки газ опускается вниз, а по краям поднимается вверх. Интенсивность движений газа в воронке зависит от степени неустойчивости атмосферы. Восходящие потоки воздуха способны достигать значительных высот (граница тропосферы и даже выше). Кинетическая энергия возбужденной при падении запыленного облака конвекции на порядок больше энергии самого облака и сопоставима с энергией ядерного взрыва. Так, например, для случая Н = 0,9; y_d=l,l; p_cJр_а =1,4 упомянутая энергия составила приблизительно 32 мегатонны в тротиловом эквиваленте.

В заключение отметим, что время расчета каждого из вариантов, включающих более 30 000 шагов по времени, на сетке 1 000 х 1 000 ячеек на AMD Athlon-64/2800 составило около 75 часов.