Применение задач сопротивления материалов к решению проблем биомеханики

С понятием прочности люди столкнулись в давние времена. Английский антрополог Dart (1925) предположил, что первой культурой была остеоодонто-кератическая культура, поскольку первыми орудиями труда, защиты и быта были палки из стволов и веток деревьев, камни, костные структуры животных. Так, на Афонтовой горе возле Красноярска археологи обнаружили челюсть детеныша мамонта и несколько каменных и костяных орудий труда эпохи палеолита [17]. Предположительный возраст находок составляет около 16 тысяч лет. Древние орудия из кости использовались рыболовами Северной Европы 8000 лет назад, а в залах музеев мира можно видеть разнообразные предметы быта, которые изготовлены 3100–2700 лет до н.э. из зубов мамонта, гиппопотама или других животных. Исследователи прошлых лет пытались понять устройство и функционирование биоконструкций.

• •    Аристотель (384–322 гг. до н.э.) одним из первых применил геометрический анализ к описанию механического действия мускулов при движении частей или всего тела.

• •    Попытки обоснования связи формы костей с приложенными механическими усилиями были предприняты в 1638 году Галилео Галилей (1564–1643).

• •    Уильям Гарвей (1578–1657) и Рене Декарт (1596–1650) в своих работах отметили сходство между людьми и механизмами.

• •    Английский ученый Роберт Гук (1635–1703), сформулировавший основной закон механики о зависимости между напряжениями и деформациями, ввел понятие «клетка» в качестве основного элемента живых организмов.

• •    Леонард Эйлер (1707–1783) одним из первых обратил внимание на необходимость учитывать изменение свойств тканей кровеносных сосудов.

• •    В 1866 году врач Мейер ( Meyer ) в Цюрихе и профессор Кульман ( Culmann ) из Цюрихского политехникума на примере бедренной кости показали, что

  © Демидова И.И., 2009

Демидова Ирина Ивановна, к.ф.-м.н., с.н.с. НИИ математики и механики, СПб строение костной ткани соответствует законам механики, в частности, траектории трабекул губчатой ткани совпадают с линиями максимальных напряжений и сопоставили напряженное состояние костей с распределением напряжений в деталях башенного крана. Подобные рассуждения и рисунки можно встретить, например, в учебнике Н.А. Белелюбского «Строительная механика» (1897) и в монографии члена-корреспондента АН СССР, профессора Ленинградского университета Г.В. Колосова «Применение комплексной переменной к теории упругости» (1935).

В истории науки таких примеров можно найти много.

Биоконструкции характеризуются сложной структурой, системой взаимоотношений элементов и физико-механическими свойствами тканей их компонентов (α k ), изменяющимися во времени. При этом параметры α k зависят не только от изменения внутренних параметров, но и от внешних параметров β j окружающей среды и времени t .

^a к = ^{f (а} 1 , ^а 2 , -,^а к -1 , ^в j , t )

Анализ элементов системы «биоконструкция–окружающая среда» показывает, что эта система является многопараметрической с взаимозависимыми параметрами, изменяющимися во времени. Для решения таких задач применяется системный анализ, выявляются все факторы, влияющие на состояние и функционирование биосистемы. В общем виде система уравнений механики твердого тела при учете изменения всех факторов и анизотропии структуры тканей очень сложна, поэтому для изучения функционирования биосистемы, для выявления зон возможных разрушений в системе применяются различные методы физического и математического моделирования. Для механического описания проблем нередко применяются модельные задачи, имеющие аналитические решения, от одноосно растянутого или сжатого стержня до сферы или цилиндра, нагруженных давлением [3]. Такие модели, как правило, можно использовать для получения качественной картины распределения напряжений и для вычисления интервала возможного изменения параметров при действии нагрузок.

Модельные задачи

Одноосное растяжение или сжатие. При приложении силы Р к образцу в опытах на растяжение или сжатие (рис. 1) в нем возникает напряжение о .

о = P^F,(1)

где F – площадь поперечного сечения, при этом начальные размеры образца изменяются на A l = l - l 0 , т. е. образец деформируется:

8 = (l — 10 )/l0-(2)

Деформация ε1 в осевом направлении

81 = о/ E.(3)

Формула (3) – это закон Гука. Для трубчатых костей, стволов растений или однокорневого зуба за модель можно принять полый цилиндр и вычислить напряжения и деформации, возникающие при действии вертикальной нагрузки (собственного веса или жевательной нагрузки). При этом в качестве критерия оценки напряженно-деформированного состояния для костей принимается критерий достижения

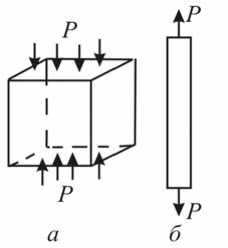
Рис. 1. Модели

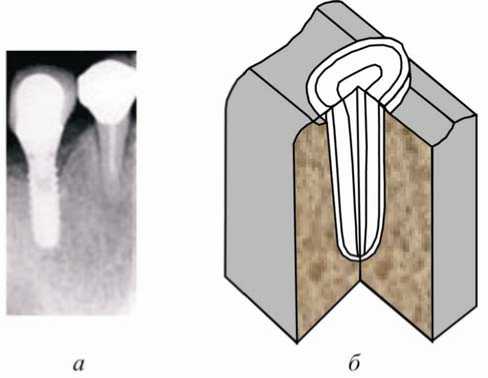
Рис. 2. Челюсть с имплантатом и живым зубом ( а ), строение зубочелюстного сегмента ( б )

максимальных растягивающих напряжений, поскольку, например, для твердых тканей зуба предел прочности при растяжении значительно меньше, чем при сжатии:

σ ≤ σ р .                                        (4)

Для мягких тканей связок или Ахиллова сухожилия используется критерий допустимых деформаций ε^∗ .

ε(σ) ≤ ε∗.                                           (5)

Разрыв волокон периодонта происходит на этапах операции удаления зубов – люксации, ротации и тракции [12], а Ахиллова сухожилия – при растяжении, возникающем чаще всего у спортсменов при действии длительных или динамических нагрузок.

Эту же модель нередко используют при моделировании функционирования стержневого имплантата [13].

Но следует сразу же отметить разницу между действием вертикальной нагрузки на зуб и на имплантат (рис. 2, а ). Зуб находится в лунке и соединяется с костью челюсти периодонтальными волокнами (рис. 2, б ). Зуб как бы подвешен в лунке и на боковые поверхности зуба действует давление в периодонтальной ткани. А имплантат вколачивается или ввинчивается в кость челюсти, и на боковые поверхности имплантата действует давление со стороны челюсти. В этом случае для получения более полной информации о влиянии имплантата на кость челюсти лучше использовать задачу о действии нагрузки на колонну, заключенную в жесткую трубу [14].

Модель составного стержня при растяжении можно использовать при моделировании третьего этапа удаления зубов – тракции, перед началом которого после разрыва боковых волокон остается часть волокон периодонтальной ткани [13].

Анализ возможности разрушения зуба до разрыва волокон проводится с применением критериев прочности для дентина и волокон периодонтальной ткани.

Внецентренное растяжение или сжатие . Наличие кариозных поражений и искривление корня зуба при жевании или тракции, т.е. при одноосном растяжении или сжатии, вызывают дополнительный момент M (рис. 3).

В случае если ось зуба не совпадает с линией действия сил, моменты М х и М у от силы Р , приложенной в точке с координатами х 0 , у 0 , будут М х = Ру 0 , М у = Рx ₀ [1]. Тогда нормальное напряжение записывается в виде

P Py ₀ y Px ₀ x

.

с = —I---1--

FI x I y

Наибольшие напряжения имеют место в точках, наиболее удаленных от нейтральной линии. Например, если кариозная полость составляет 1/4 площади сечения зуба, то напряжения увеличатся на 1/3 по сравнению с интактным зубом, если она составляет 1/2, то увеличение будет четырехкратное.

При кручении круглого стержня радиусом r парами сил с моментом М , приложенными к концам стержня (рис. 4), напряжённое состояние стержня характеризуется возникновением касательных напряжений т _тах , определяемых по формуле

Т max

MrM

J T" w ’

где J p – момент инерции, зависящий от геометрии стержня. Из формулы (7) следует, что максимальные значения напряжений будут достигнуты на внешней поверхности стержня. Угол закручивания ф определяется формулой

Ml

GJp , где G - модуль сдвига, у - относительный сдвиг, l - длина стержня.

Кручение в биоконструкциях возникает, например, при действии ветра на растения, при выполнении человеком физических упражнений, при падении на склоне горы или оврага, в автокатастрофах, при экстракции зубов с нарушением формы корня методом ротации [9]. Формула (8) показывает, что величину угла закручивания ф , например, при удалении зубов можно регулировать только нагрузкой, поскольку ни длину ( l ) стержня (зуба), ни размеры поперечного сечения ( r ), ни состояние тканей

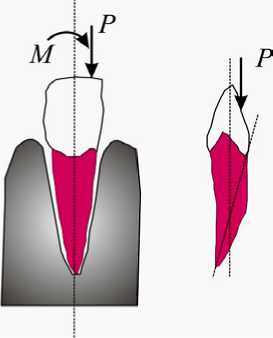
Рис. 3. Внецентренное сжатие в зубах

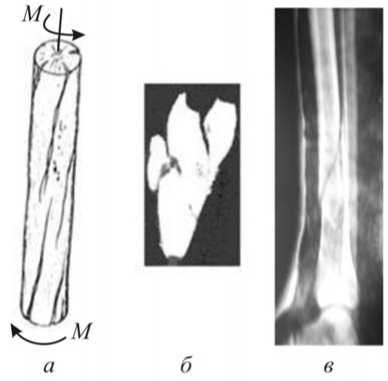
Рис. 4. Схема кручения ( а ), разрушение зуба ( б ) и кости ( в )

Рис. 5. Модели при чистом изгибе (а), (б), распределение напряжений и интерференционные полосы (б)

конструкции ( G ) изменить невозможно, при этом разрушение идет по винтовой линии (рис.4, б ).

Отметим, что величина модуля G , так же как и модуля Е, зависит от состояния твердых тканей зуба или костей (возраста, заболеваний, степени минерализации тканей). Поэтому и угол ф согласно формуле (8) будет определяться состоянием тканей и изменяться, например, для зуба от 1,3 до 35 . Максимальные значения этих углов получены для максимального значения прочности при растяжении О р . Достигнуть максимальных углов можно, если корень имеет большое искривление или врач прикладывает резкие, скачкообразные усилия. Аналогичные разрушения можно наблюдать в клинике на трубчатых костях (рис. 4, в ) [2].

Чистый изгиб. Напряжение о в случае чистого изгиба пропорционально расстоянию от нейтральной оси:

о = M y / I ,                                     (9)

где I – момент инерции сечения относительно нейтральной оси (для круглого сечения диаметром d момент инерции I равен пd 4 /64), у - расстояние от нейтральной оси, l – длина всей балки. Если к концам образца приложить нагрузки или изгибающие моменты, как показано на рис. 5, то образец прогнется, принимая изогнутую, искаженную форму.

Консоль. На рис. 6, а приведена интерференционная картина в консоли и в заделке [15].

Из решения задачи для консоли известно, что наибольшее напряжение возникает в области заделки. При таком деформировании ткани биоконструкции оказываются растянутыми со стороны силы Р , а на противоположной стороне – сжатыми, и разрушения следует ожидать в области заделки со стороны приложения

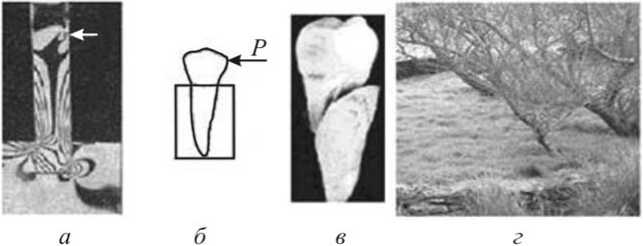
Рис. 6. Интерференционная картина в модели консоли ( а ), возникновение изгиба в биоконструкциях ( б , г ) и разрушение зуба при люксации ( в )

силы, где растягивающие напряжения наибольшие. Допустимое значение силы Р** для модели в виде сплошного цилиндра диаметром d вычисляется по формуле

P_# _ 0,1 d ³ и

S, где S – длина цилиндрической консоли балки. Таким образом, чем больше S, тем меньше величина допустимой нагрузки и возрастает опасность возникновения трещин. Из формулы (10) видно, что величина нагрузки Р зависит от размера биоконструкции d и его состояния стр. Консоль и шарнирно опертые балки являются наиболее часто встречающимися моделями в живых системах. Это стволы и ветви растений, зубы животных и человека и т.д. Наибольшее количество приложений для человека относится к зубочелюстной системе. Первым на действие горизонтальной нагрузки Рх на зуб при жевании обратил внимание Synge в 1931 году. Эта нагрузка Рх мала по величине и действует только во время жевания, поскольку зуб под действием жевательной нагрузки не только сжимается, но и может изгибаться, особенно если жевательная нагрузка приложена на часть окклюзионной поверхности или при возникновении резорбции на корнях [4]. Кроме этого, горизонтальная нагрузка возникает в зубочелюстной системе и в других ситуациях:

• 1)    давление соседних зубов, вызванное различными причинами (ростовые деформации, остатки пищи, выступающая пломба);

• 2)    заболевание бруксизмом;

• 3)    использование зубов в качестве опор для мостов;

• 4)    применение опорно-удерживающих кламмеров;

• 5)    при ортодонтическом лечении;

• 6)    при лечении переломов нижней челюсти;

• 7)    при удалении зубов на втором этапе – люксации и т. д.

В ситуациях 1–6 нагрузка Р x действует непрерывно и представляет наибольшую опасность для состояния зубочелюстной системы, поскольку при этом не только может разрушиться зуб (рис.6, в ), но и будут происходить изменения в окружающих его тканях.

Поскольку между зубом и стенкой альвеолы имеется некоторое расстояние (альвеолярная щель), то предлагается модель упругой балки, вставленной в жесткое основание с малым зазором . Математическое решение подобной задачи рассмотрено в монографии [15]. Если зуб используется в качестве опоры, то воспаление возникает именно в области касания зуба с лункой, т.е. в точках А и В (рис. 7).

Трехточечный изгиб может возникнуть в ветви челюсти при ударе или падении при поперечном ударе по трубчатым костям (рис. 8). При этом виде деформирования при приложении силы Р возникает момент сил, имеющий наибольшее значение на опорах М _ PL / 2, максимальный прогиб y max вычисляется по формуле

У max _ PL ³ /48 EI .                                (11)

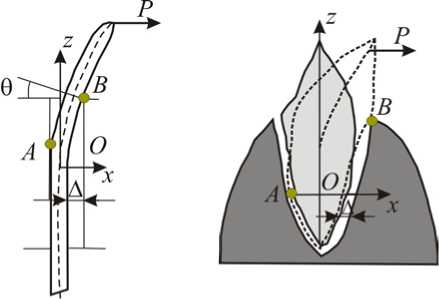
Рис. 7. Модель балки, сегмент зуба

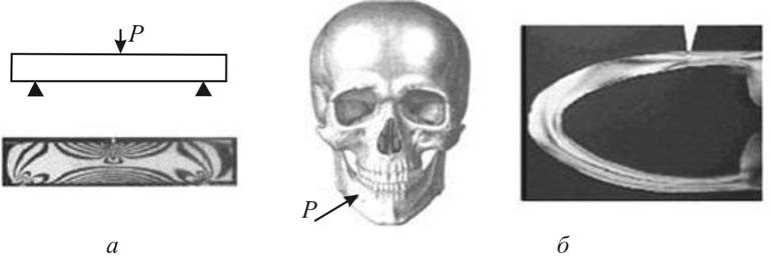
Рис. 8. Схема нагружения и интерференционная картина при трехточечном изгибе ( а ). Боковой удар и интерференционная картина в модели челюсти ( б )

На противоположной стороне от приложения силы возникает растяжение, и, согласно данным о прочности на растяжение костных тканей, в этой области начнут появляться трещины.

Заметим, что модель, изображенная на рис.8, б , – это модель кривого бруса . В кривом брусе максимальные напряжения возникают в области с наибольшей кривизной и имеют различные знаки на внутренней и внешней поверхностях.

Аналоги кривого бруса можно встретить в следующих биоконструкциях: в костях таза, в зубочелюстной системе – челюстные кости, зубы-моляры, лунки зубов в поперечном сечении. При изменении давления в периодонтальной щели в лунке зуба моляра (рис. 9, а ) возникает концентрация напряжения около шейки зуба и в фиссурах [6, 10]. Нижнюю челюсть можно представить в виде набора кривых брусов: подбородочного отдела и ветви нижней челюсти, угла нижней челюсти, мыщелкового отростка (рис. 9, б ) [5].

Исследования механических свойств тканей

Заметим, что рассмотренные выше модельные задачи используются для получения исходных характеристик тканей биоконструкции. Для этого изготавливают образцы разной формы. Но следует отметить, что при изготовлении образцов изменяются внешние и внутренние параметры, действующие на элемент, снимаются собственные напряжения биоконструкции и ее элементов. Поэтому получаемые данные имеют относительные значения. Кроме этого, свойства тканей или элементов конструкции существенным образом зависят от ряда параметров, таких как влажность, гидростатическое давление, время и т.д.

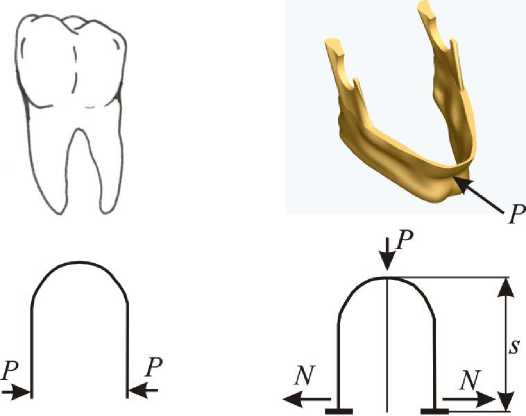
а                      б

Рис. 9. Биомеханические модели: а – моляр, б – нижняя челюсть

Первые лабораторные исследования по определению механических свойств тканей человеческого тела были получены Вертгеймом ( Wertheim ) в середине ХIХ века. Заметим, что именем ученого был назван закон в фотоупругости – закон Вертгейма, связывающий измеряемые поляризационно-оптические характеристики в оптически чувствительных материалах с напряжениями (см. рисунки в этой работе).

Согласно материалам, изложенным в монографии Messerer (1880), немецкие ученые Bruns (1854), Hyrtl (1857), Cohnstein , Weber (1859) и французский исследователь Félicet (1873) получили первые количественные результаты по прочности головы. Затем в 1876 году Rauber выполнил детальные исследования прочности материала костей, провел опыты по изгибу образцов кости и на кручение костей. В 1880 году вышла монография доктора Messerer , в которой он привел данные исследователей и свои о прочности костей скелета. Автор проводил опыты в механической лаборатории Политехнического института и поблагодарил за предоставленную возможность профессора Баушингера ( Baushinger ), известного специалиста по механике деформируемого твердого тела.

В России этому вопросу первым большое внимание уделил анатом профессор П.Ф. Лесгафт (1837–1909). Он собирал данные о физико-механических свойствах живых тканей организма человека и животных [8]. С 1885 года начались работы с сотрудниками механической лаборатории Санкт-Петербургского института путей сообщения, возглавляемой Н.А. Белелюбским, по исследованию прочности костей черепа и таза на машине Вердена [1]. Позднее данные о прочностных свойствах костей и о зависимости строения костных структур от расположения линий главных напряжений были включены в учебник Н.А. Белелюбского «Строительная механика», 1897 [2].

Сравнительные данные о прочности костей бедренной кости при растяжении, сжатии и изгибе приведены в таблице [11].

Сравнительные данные о прочности костей бедренной кости при растяжении, сжатии и изгибе

Е , МПа	σ р , МПа	σ с , МПа	σ изг , МПа
2 10 4	74–134	120–200	180

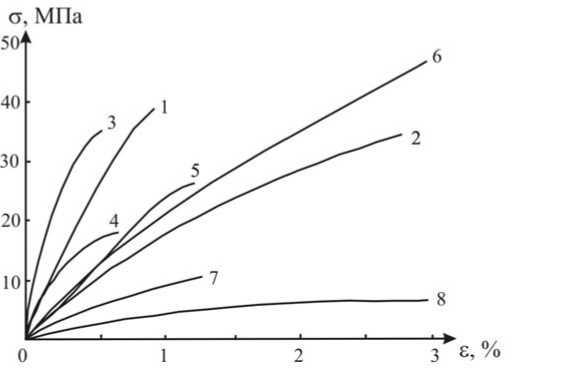
Рис. 10. Зависимость напряжений от деформации при сжатии для твёрдых тканей зуба и различных пломбировочных материалов: 1 – эмаль; 2 – дентин; 3 – твёрдое золото; 4 – мягкое золото; 5 – силикатный цемент; 6 – амальгама; 7 – цинк-фосфатный цемент;

8 – резина

Средняя прочность костной ткани при кручении 8 кг/мм² ( Rauber ).

Для примера на рис. 10 приведен график деформирования ( о , а ) тканей зубов и различных пломбировочных материалов [16].

Костная ткань, особенно спонгиозная, обладает неупругими свойствами (см. рис.10, кривая 2). Модельные задачи также используют для оценки неупругих свойств тканей путем измерения в экспериментах параметров в зависимости от времени. Например, Black (1895) одним из первых заметил изменение размеров образцов из зубов после их изготовления. Кроме того, он обнаружил, что после снятия нагрузки размеры кубика восстанавливались. Если образец из неупругого материала нагрузить силой Р(t) = const = Р0 (а(t) = о0), то будут наблюдаться изменения его размеров. В формуле (3) модуль Юнга Е уже не будет постоянным, т.е. изменение деформации а (t ) = D (t) о0 = о0/E (t).                                 (12)

D ( t ) – функция ползучести. После снятия нагрузки P ⁰ в момент t ₁ будет происходить восстановление.

а ( t ) = о⁰ [ D ( t ) - D ( t - 1 1 ) ] .                                (13)

Практически в области линейной ползучести происходит полное восстановление, т.е. деформация а ( t ) ^ 0, материал обладает обратимой деформацией. На рис. 11 приведены кривые ползучести и восстановления костной ткани [7]. Момент разгрузки соответствует значению t _к = 288 мин, при t > t _к происходит восстановление.

Такой процесс подобен процессам, происходящим при заживлении костной ткани после переломов или лунки после удаления зубов и изменения размеров отломков при переломах челюсти. Если величина деформации не достигнет начального значения, то появится остаточная деформация, которая будет влиять на последующие циклы деформирования.

Неупругостью костной ткани и наличием остаточных напряжений и деформаций можно объяснить характер области перелома костей. Для этого используем задачу об изгибе. Разрушение при изгибе костных тканей зависит от структуры и состояния кости, а также от ее конструкции. Если бы кость была упругой, то разрушение произошло бы на две части (рис.12, а ), а для неупругого материала после разрушения

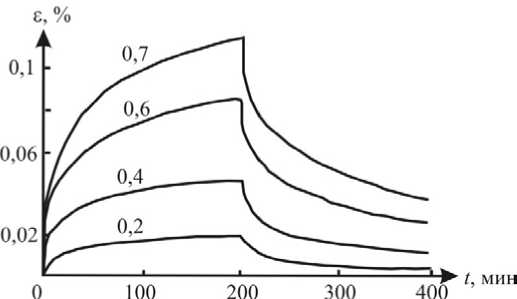
Рис. 11. Кривые ползучести и восстановление костной ткани

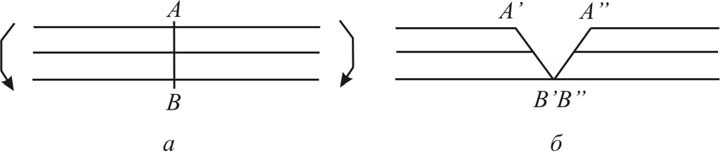
Рис. 12. Схема перелома тканей кости при изгибе: а – для упругого материала, б – перелом при изгибе с учетом неупругости материала

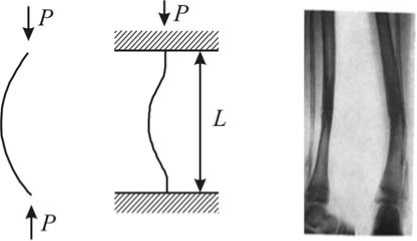
a                    б

Рис. 13. Сжатый стержень ( а ), дугообразное искривление кости ( б )

при соединении отломков образуется треугольник (рис 12, б ), так как на растянутой стороне накапливаются деформации растяжения, а на противоположной – сжатия. С таким видом разрушения нередко сталкиваются хирурги при операции на костях [5]. Заметим, что поверхность разрушения А’В’ – А’’В’’ (см. рис. 12, б ) на практике имеет более сложную поверхность из-за наличия тонких поверхностных слоев.

Задача Эйлера. В 1757 году Эйлером была выведена формула для определения критической нагрузки P при сжатии упругого стержня длиной L (рис. 13, а ).

2 EI P = π _{L 2} ,

где Е – модуль Юнга, I – момент инерции сечения.

Спустя почти сто лет формула (13) была применена для расчета прочности железнодорожных мостов, и модель Эйлера принесла практическую пользу в проведении экспериментов. Такая потеря устойчивости возникает в трубчатых костях при размягчении тканей, связанном с некоторыми заболеваниями, например рахитом, или при перегрузках юных спортсменов (рис. 13, б). В биомеханике формулу (13) можно применить для оценки допустимой нагрузки на кости в зависимости от состояния тканей, т.е. при учете изменения величины модуля Юнга от времени, возраста, соотношения компонентов структуры и других параметров. Такие исследования особенно необходимы при разработке программ работы с детьми для занятия спортом.

Заключение

Перечень задач сопротивления материалов, которые можно использовать в качестве модельных в биомеханике, значительно шире. Но следует отметить, что в живых конструкциях важное влияние на функционирование конструкции и состояние свойств тканей оказывает давление как внутреннее, так и внешнее, поэтому состояния одноосного растяжения или сжатия практически не бывает. Кроме этого, внешние и внутренние воздействия не постоянны и имеют волновой характер.