Применения Z-преобразования на датчике температуры

Автоматическое управление предприятий во многих параметрах имеет место в требовании обеспечить желаемого качество передачи информации, то есть передачи дискретных сигналов z-преобразование. Наряду с другими законами автоматического регулирования оставляет существенный след в теории сигналов, так как, в настоящем времени множество предприятий основываются всего лишь на нескольких методах в самом преобразовании. Актуальность закона z-преобразования в том, что он существенно помогает выбрать определённую сигнала, рассчитать эту полезность, а также определение квантования по времени задержки и по уровню, вычисление отсчетов.

Целью данной работы является изучение области применения z-преобразования на предприятиях. Масштабность работы в том, что имея в виду, использующиеся огромное количество разных датчиков и измерительных приборов в автоматизацию промышленных предприятий требуют получить из аналоговых данных оцифрованные дискретные сигналы для автоматического регулирования датчиков температуры с применением z-преобразование. Модель датчика температуры с применением z-преобразования рассмотрен с рассчитанными коэффициентами.

При разработке системы автоматического регулирования важно учитывать внешние воздействия, характеризующие стабильность работы системы для характерного понимания, обычно используют дискретную модель сигналов, а для получения нужных значений устойчивости применяют z-преобразование, нужно понимать, что под этим методом понимается соотношение входов и выходов, то есть, если на входе вводится данные аналогового вида, а на выходе получают преобразованные дискретные сигналы.

Метод имеет несколько критериев применения, во-первых, система должна быть в замкнутом контуре, во-вторых, система не должна зависеть от двух переменных. В методе z-преобразование всегда должны присутствовать коэффициенты усиления.

Применение данного метода рассмотрена к задаче X(t)=t*exp(-at), где присутствует z-изображение функции. Используя теорему об умножении на экспоненту, применительно можно записать функцию следующим образом:

Z = { t • exp ( - at ) } =

T_oz • e^at _ T_oz • e at ( z • e at - 1 ) 2 = ( z • e at ) 2

Передаточная функция (1) представляет разомкнутую дискретную систему по аналогии с непрерывными системами. Введем в рассмотрение передаточную функцию дискретной системы W(z), как отношение Z-изображений выходного и входного сигналов при нулевых начальных условиях:

вых z

Хвх (z)

В разомкнутой дискретной САУ (рис.1) сигналы X(t) и X_ВЫХ(t) непрерывные функции времени, и формула определяет связь не между ними, а соответствующими решетчатыми функциями [ nT₀ ] и Хвых [ nT₀ ].

Рис.1. Определение дискретной передаточной функции

Моделирование датчика температуры с z-преобразованием

Данная работа выполнена в MATLAB Simulink. Изначально некоторые данные заданы в Блоке constant:

• ❖    сопротивление терморезистора (Р),

• ❖    температурный коэффициент сопротивления (Б),

• ❖    начальная температура по шкале Кельвина (Т0).

С помощью блока ramp задан необходимый диапазон изменения температура. Параметром Slope определена крутизна характеристики, которая обеспечивает изменение напряжения в необходимом диапазоне.

Исходные данные объединены блоком mux , которые поступают на блок Fcn , где задана передаточная функция F(z)=(0,07*z)/(z-0.93) изменения напряжения от температуры. В данном блоке получено преобразование сигнала, который после поступает к блоку gain , с помощью которого задается диапазон изменения выходного напряжения в пределах 0÷5В. Модель датчика температуры приведена на рисунке 2.

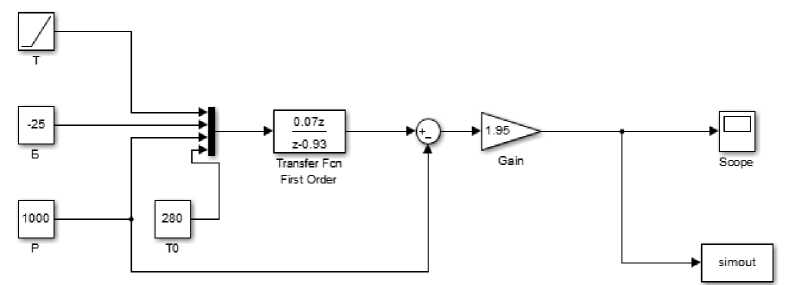
ToWoikspece

Рис.2. Модель датчика температуры

Переходные характеристики датчика температуры показаны в графике (Рис.3). По выведенным на график характеристикам видно, как данное преобразование оказывает полезность и точность корректировки сигналов на входе датчика.

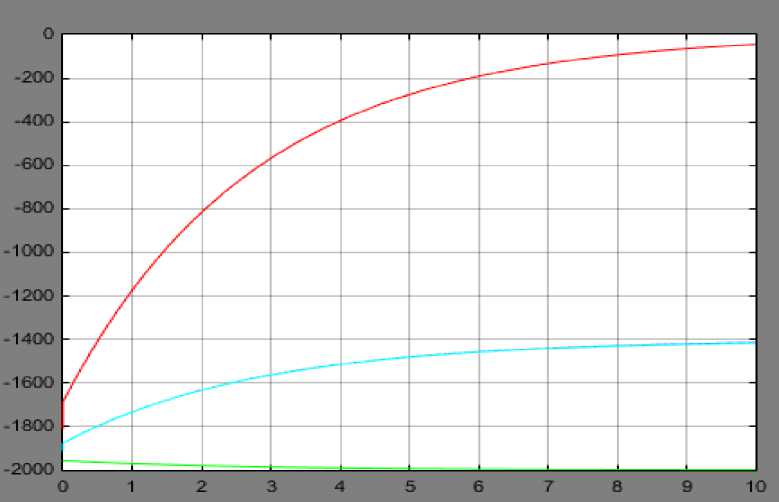
Рис.3. Полученные графики после z-преобразования

В заключение можно указать то, что алгоритм работы модели аналогичен алгоритму работы реального программного обеспечения датчика; полученная модель позволяет наиболее полно оценить влияние частоты квантования по времени задержки и по уровню на динамические характеристики системы. И так можно сделать вывод, что внедрение z-преобразования оправдывает все возложенные ожидания.