Примеры точных решений нелокального волнового уравнения с нелинейными источниками

—

w ²

52г     2д4г      z ,

.  — X -7 = ku(т), дx      дx

где т - функция, характеризующая некоторое физическое свойство среды; t - время; x - декартова координата; w - скорость распространения малых возмущений; k _u ( т ) - функция источника;

exX - параметр слабой пространственной нелокальности, см. [1] и указанную там библиографию. В монографиях [2, 3] изложены прикладные аспекты задач о волновых процессах в про- странственно нелокальных средах.

Для перехода к безразмерной формулировке применяем масштабы т_ь, t b : ( Фь ) ^ t , [ x ( ^wtb ) ]^ x ', ( V^T b ) ^ ^т , [ ( k u t b )/ ^T b ] ^ k u , [ x 2/ ( w 4 t 2 ) ] ^ ( ex 2 ) .

В результате получаем следующую форму записи нелокального волнового уравнения в пределе слабой нелокальности д2 т    д2т

------— д t ²    д ( x ') 2

—

^{£Х 2} дИ ⁼ k " ^{( T} ) •

При е = 0 имеем в (1) уравнение Клейна-Гордона, которое позволяет исследовать нелинейные волны различной физической природы [4, 5]. Современные результаты и библиография исследований нелинейных гиперболических уравнений с источниками даны в [6–9]. Набор известных в литературе точных решений нелинейного уравнения Клейна-Гордона представлен в [10].

Цель данной статьи - рассмотреть для нелокального уравнения (1) новые точные решения типа бегущей волны в среде с источником к _и ( т ) , имеющим синусную либо полиномиальную нелинейность.

Преобразование волнового уравнения. Уравнение (1) запишем в виде системы, определяющей две неизвестные функции т , 6 :

д ² т     д 20    ,    „         ₂   д ² т

— ку, 0 — т+ £Х        • д t2    д( x’ )2 U                д( x ')2

Обозначим д т/дx' — u, д т/дt — v, и тогда (2) принимает вид дv    д20    ,   „

— ——у ^— k и , ^{0 — т+} X ^д t   д ( x’ ) 2

2 д u  д u _ дv дx' ’ д t   дx'

•

Выполним преобразование независимых переменных является следующая форма записи уравнений (3) [11]:

( x ', t ) ^ ( t, t ) . Результатом вычислений

д v   д v

--+ v--u д t    д т

д u д0 д т д т

д20

+ u —- — k ,

^{2 u}

д т

„       ₂ д u  д u    д u    S v

0 — Т+ £Y u--,--+ V--— u-- • д т д t д т д т

Рассмотрим автомодельный вариант u = и ( т ), v = v ( т ), для которого v — — uM , т = т ( Z) , Z — x ' — Mt , M - const •

Скорость перемещения линии Z = const равна N — dx! dt . Число Маха M — N / w определяет дозвуковой ( M ² <  1) либо сверхзвуковой ( M ² >  1) скоростной режим. Уравнение (5) запишем в виде

0 — т+ £Х2 dU, U — u2/2, д т подставим в (4) и в итоге получим d dτ

U M ²

—

d ² U

1—ex dτ

—

2 d3U eX U     — kи • dτ

Зависимость искомой функции т = т ( Z ) от волновой координаты Z определяется выражением d т

-----тут — ± d Z •

( 2 U ) 1 ²

Обсудим частные примеры зависимостей U — U ( т ) , позволяющие проинтегрировать (7) в конечном виде и получить физически содержательные функции источника к _и ( т ) •

Синусная нелинейность источника. Обозначим т ' — n т, где n - произвольная положительная константа. В формуле (7) возьмем знак «+». Пусть ( 2U ) 12 — A cost ' , А = const. Решение типа кинк, описывающее переход между двумя состояниями равновесия системы «среда - источник», имеет вид

т

- П ± 2arctg [ C 1 exp ( n ^ A ) ] , C 1

> 0, Z е ( -” , ^ ) ; A , C i — const.

Здесь верхний знак «+» относится к области определения решения Т е ( -П 2, П 2 ) . Наклон кинка положителен при А >  0: Z ^-^да , Т ^ ( -П 2 ) ; Z ^^ , Т ^ ( П 2 ) . Наклон отрицателен при А < 0: Z ^-» , т ' ^ ( П 2 ) ; Z ^^ , т' ^ ( - П 2 ) . Знак «-» перед арктангенсом в (8) относится к интервалу т ' е ( - 3 П 2, - П 2 ) . Наклон этого кинка отрицателен при А >  0: Z ^ -^ , т ' ^ ( - П 2 ) ; Z ^^ , Т ^ ( - 3 П 2 ) . Наклон положителен при А <  0: Z ^-^да , Т ^ ( - З л/ 2 ) ; Z >^ , т' ^ ( -я/ 2 ) .

Данный процесс генерируется источником ки nn = k2 sin 2т' + к4 sin 4т'; k2, k4 - const.                             (9)

При е ^ 0 свойства коэффициентов k ₂, к ₄ и их связь с параметрами задачи состоят в следующем:

A ² = ( - 4 к 4 З Ъх ² n ² ) 1 ² , е к 4 <  0;                             (10)

M ² = 1 + -2 | 4 к₄

A ² 1 3 4

—

k ₂

Если к2 <(4к4/3), то процесс сверхзвуковой. «Звуковое» решение M2 = 1 получаем при к2 = 4к4 /3. Дозвуковой режим движения кинка наблюдается при к2 >( 4 к4/3) , (-к43х 2 )>[ к2 -( 4 к4/3)]2 .

Последнее неравенство всегда будет выполнено при достаточно малом | е| х ².

Итак, порядок вычислений следующий. Заданные параметры к ₂, к ₄ определяют скоростной режим движения кинка. Область определения решения соотносится с выбором знака «+» или «–» в (8). По формулам (10), (11) подсчитываем A ², M ². Посредством произвольной положительной константы С 1 задаем начальное значение т' ( Z = 0 ) . Далее указываем знак А , т. е. фиксируем знак наклона кинка. Выбор знака величины М указывает направление его движения.

Формулу (11) можно представить в виде M2 = 1 + £1 [(4к4/3)- к2 ]V3, который позволяет проследить зависимость скорости движения кинка от параметра нелокальности среды £1 =(-ех2/к4)^ >0. А именно: в сверхзвуковом режиме d(M2)/д£1 >0, в дозвуковом режиме

d( m 2 )/д £1 < о.

Обсудим свойства функции источника (9), применяя выражение к _и /п = sin2 т ' ( к ₂ + 2 к 4 cos2 т ') , т ' е ( - 3 П 2, П 2 ) .

При всех скоростях движения к _и = 0 там, где sin 2 т ' = 0, т. е. при т' = - 3 П 2, - л , - п /2, 0, л /2. Существование либо отсутствие других корней т ' = т ' уравнения к _и ( т ' ) = 0 связано со знаком параметра ех ² и со скоростным режимом M ². Для сверхзвукового процесса корни вида т ' = т ' , к _о ( т ' ) = 0 существуют при следующих условиях: 1) г < 0, к ₄ > 0, 0 < (- к ₂) < 2 к ₄, cos 2 т ' >  0; 2) г < 0, к ₄ > 0, 0 <  к ₂< 2 к ₄, cos2 т ' <  0; 3) г > 0, к ₄< 0, (3 к ₂/4) <  к ₄<( к ₂/2) < 0, cos2 т ' <  0. Для дозвукового процесса: 1) г < 0, к ₄ > 0, 0 <  к ₂< 2 к ₄, cos 2 т ' <  0 ; 2) г > 0, к ₄< 0, 0 <  к ₂< (- 2 к ₄), cos2 т ' >  0; 3) г > 0, к ₄< 0, (4 к 4 /3) <  к ₂< 0, cos2 т ' <  0.

Отметим немонотонную зависимость M2 от параметра источника к4: d(M2 )/дк4 = 0, если к4 = (-3к2/4), т. е. функция (12) равна ки nn = 2к4 sin2т'[cos2т' -(2/3)^ .

В сверхзвуковом режиме имеем минимальное значение ( M ²) _mi n при к ₄ > 0, s < 0, к 2 = ( - 4 к ₄/3 ) <  0. В дозвуковом режиме максимальное значение ( M ²) min достигается при к ₄< 0, s > 0, к ₂ = ( - 4 к ₄/ 3 ) > 0. Это значит, что соответствующие до- и сверхзвуковому режимам источники вида (13) отличаются один от другого инверсией областей к _и >  0 и к _и <  0. На рис. 1 схематически показан пример такой инверсии для cos2 т ' = 2/3, т ' е ( — П 2, П 2 ) .

Отдельный вариант к2 = 0 (см. (9)-(11)) представляет собой точное решение (8) нелокального уравнения синус-Гордона, для которого ки/п = к4 sin4т, Т = пт, n > 0, M2 = 1 + (8к4/3А2). (14) Здесь А2 по-прежнему определяется формулой (10). Движение кинка дозвуковое при г > 0, 0 <(-к4 )<[3,1б£%2]. Сверхзвуковой режим имеем при г < 0, к4 > 0.

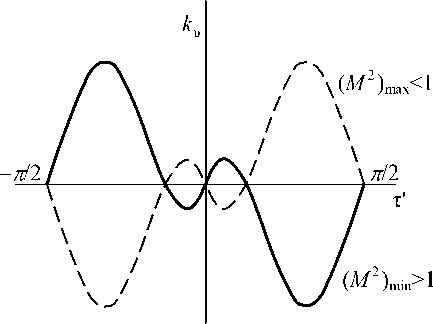
Рис. 1. Инверсия областей k υ > 0 и k υ < 0 для источников (13), соответствующих экстремальным скоростям движения кинка

Важный частный случай решения (8)-(11): если s = 0, то к4 = 0, А - произвольная постоянная, и функция (8) - это известное решение [4, 5] уравнения синус-Гордона, ку = пк2sin(2пт), M2-1 = (-2к2/А2).                         (15)

Здесь M2 > 1, если к2 < 0; 0 < M2 < 1, если 0 < к2 <(А2/2). Своеобразие ситуации в том, что аналитическая структура кинка (8) одинаковая для классической (s = 0) и нелокальной (s ^ 0) сред. Основные различия между этими процессами видны из формул для M 2 в (14) и (15). Возь- мем для наглядности одинаковые источники:

п* = 2п0 = 4п£, к* = п0к2 = п£к4, п0 > 0, п£ > 0, т. е. sgnк2 = sgnк4, ки = к* sin(п*т), где нижние индексы «0» и «ε» относятся к классической и нелокальной средам соответственно. Тогда имеем

M 2 = 1 - 2 к 2/ А ² , M 2 = 1 + 8 к 4/ (3 А £ ).

Следовательно, различаются области определения решений и скоростные режимы (дозвуковой -сверхзвуковой) движения кинков.

Кубическая нелинейность источника. В формуле (7) применяем оба знака «±». Возьмем

(2U)12 = т (А2 + А3 т)12; А2, А3 - const(16)

и получим т=--4C1 A2E.2 ’ E = exp(±ZVA2),(17)

А3 (1 - C1E )2           '   ’'

■  = ±^ 4A2 C1E (1 + C E) .(18)

d C      ²   A 3 ( 1 - C , E ) ³

Величина т ( Z = 0) зависит от выбора константы С i > 0.

Вариант 1: слабый разрыв. Пусть A ₂> 0, A ₃> 0, т > 0, 0 <  C ₁< 1. Решение (17) содержит две ветви, смыкающиеся при Z = 0 и образующие слабый разрыв функции т ( Z ): при Z = 0 терпит разрыв первого рода первая производная dт / d Z, см. верхнюю часть рис. 2. В формуле (18) знак «+»

относится к левой ветви, Z - 0 , E = exp ( Z x/ A 2 ) , dT / d Z

> 0; знак «-» - для правой ветви, Z ^ 0,

E = exp ( - Z 4A ) , d т/ d Z < 0. Здесь т ( Z = 0) > 0 для обеих ветвей.

Если A ₂> 0, A ₃< 0, т < 0, C 1 > 1, то решение (17) содержит по-прежнему две ветви, образующие слабый разрыв, но меняется конфигурация этих ветвей, см. нижнюю половину рис. 2. В формуле (18) знак «-» относится к левой ветви: Z - 0, E = exp ( — Z 4A ) , dT / d Z < 0; правая ветвь:

знак «+», Z ^ 0, E = exp ( Z 4A ) , dT / d Z > 0. Здесь т ( Z = 0) < 0.

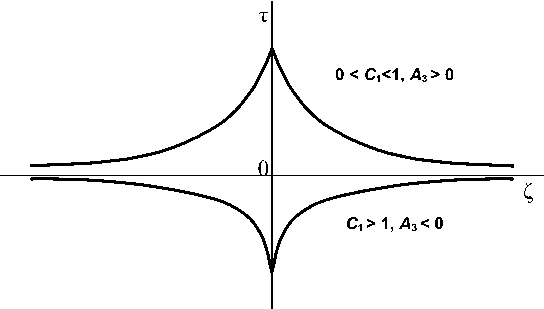
Рис. 2. Кубическая нелинейность источника (20): решение (17), содержащее слабый разрыв

Вариант 2: уединенная волна. В этом случае следует взять (- A ₂) <  A ₃ т < 0. Из (7), (16) после

интегрирования получаем гладкое решение

т = —4 A 2 E- , E = exp (+ Z JA ) , A 2 > 0, z = 0, ат / d Z = 0.

A3 (1 + E)2           v        ’

Формула (19) дает уединенные волны, различающиеся знаком функции т ( Z) : 1) т > 0 при A ₃< 0,

E = exp (-Z ^A), Z €(-», да)

(см. верхнюю часть рис. 3); 2)

т < 0 при A ₃ > 0, E = exp ( Z Д"А 2 ) ,

Z е ( -да , да ) (см. нижнюю часть рис. 3).

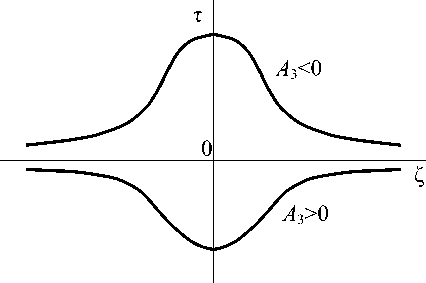
Рис. 3. Кубическая нелинейность источника (20): уединенная волна (19)

Волновые процессы, которые описываются решениями (17) и (19), вызваны воздействием источника ку = к1 т+ k3 т3 , k1 к3 < 0 ,                                    (20)

для которого выполнены соотношения

A 2 = -k Ly >  0, A ₃² =—2 k 3y >  0, M ² = 1 + 5 A i^ ² .                 (21)

• ²   4 ix ²        3     15 iX ^{2                  2}

Напомним, что для всех рассмотренных здесь вариантов A2 > 0. Следовательно, сверхзвуковой (M2 > 1) режим движения имеем для s > 0, k1 > 0, к3 < 0. Если k1 < 0, к3 > 0, 0 < (-ex2 ) < [—4/(25к1)], то режим движения дозвуковой, M2 е (0,1). Функция (20) обращается в ноль в трех точках: т = 0, т = ±(-к1 рз3 )12 . Решения (17) и (19) содержат дробь A2/A3, которая определяется только свойствами источника: A2] A2 = (—15ki/8кз) • Информация о влиянии параметра нелокальности ex2 заключена в показателе экспоненты ζA2= ( x' - Mt) 4a , где M2A2 = A2 + (5к1/4). Выбор знака константы А3 соответствует тому обстоятельству, что для слабого разрыва А3т > 0, а для уединенной волны А3т < 0.

Частный случай s = 0 дает тривиальное решение линейного однородного волнового уравнения: к 1 = 0, к3 = 0. Воздействие источника (20) обусловлено именно нелокальными (s ^ 0) свой- ствами среды.

Источник - полином пятой степени. В формуле (7) возьмем знак «+» и примем

( 2U У'² = br 1 - -2

; b , r - const.

В результате вычислений получаем

- = b th ( r Z ) , - е ( - b , b ) , Z g ( -” , ” ) .

Тогда при s ^ 0 функция кu (-) в (6) представляет собой полином, содержащий степени т, т3 и т5 - запись не приводится. Если s = 0, то член т5 отсутствует, и функция (22) - это известное [4, с. 640] кинковое решение, генерируемое источником ки = к0-

|2 - 1 1 , M ² - 1 = ( к о/2 r ² ) .

Здесь к о , r , b - свободные параметры. Скорость перемещения бегущей волны сверхзвуковая, если к ₀ > 0; скорость волны дозвуковая, если (-2 r ²) <  к ₀< 0. В нелокальном случае заслуживают внимания два частных примера, для которых к _и ( - ) содержит т и т ⁵ либо т ³ и т ⁵.

I.

Г     R\(

ки = к1- 1 - b^-^  1+b_3 , r = ki/(36ez )

к 1 е >  0, M ² = 1 - 20 r² ex ².

Сверхзвуковой режим: к < 0, к 1 < 0. Дозвуковой режим: к > 0, 0 <  к 1 <  ( 0,09/ ex ² ) .

II.

k _υ

= к з -³ 1 1 - 1| 2 1 , r ⁴ = к з b ²/ ( 36 ex ² )

к 1 е >  0, M ² = 1 - 2 r² ex ² .

Сверхзвуковой режим: s < 0, к ₃< 0. Дозвуковой режим: s > 0, 0 <  к ₃ b ² <  ( 9/ ex ² ) .

Сравним классический вариант (23) с источниками (24), (25), воздействие которых обусловлено нелокальными свойствами среды, s ^ 0. Для представленных примеров одной и той же аналитической структуре кинка (22) соответствуют функции источника (23), (24) и (25), различающиеся степенями т в отдельных слагаемых [( т , т ³); ( т , т ⁵); ( т ³, т ⁵)], но имеющие одинаковое число ненулевых действительных корней вида т = т 1 , к _и ( - 1 ) = 0 . Эти корни, соответственно, такие: ± b ; ± b ( 32 ) ¹⁴, ± b ( 3/2 ) ^1/2 .

Заключение. Получены точные частные решения нелокального волнового уравнения (1) с источниками. Для синусной нелинейности (9) источника построено кинк-решение (8). Его частным случаем является точное решение (8), (10), (14) нелокального уравнения синус-Гордона. В случае кубической нелинейности (20) указаны зависимости, которые описывают слабый разрыв (17) либо уединённую волну (19). Даны примеры (14), (15) и (23)–(25) сопоставления свойств классической и нелокальной сред. Определены условия существования дозвуковых и сверхзвуковых режимов распространения бегущих волн.