Примеси углерода в парамагнитном ГЦК-железе: ab initio моделирование энергетических параметров

Углеродистая сталь – наиболее распространённый конструкционный материал в машиностроении – представляет собой раствор углерода в железе. Обычно используется сталь на основе низкотемпературной ОЦК-фазы железа. Поэтому поведение углерода в сплавах на основе ОЦК-железа изучено достаточно хорошо [1]. Микроструктура сталей зависит от концентрации углерода, взаимного расположения атомов углерода и условия охлаждения изделий от температуры аустенизации, выше которой железо существует в виде ГЦК-фазы (γ-Fe). Эта парамагнитная фаза термодинамически стабильна в интервале температур между 911 и 1391 °С. Однако кристаллы γ-фазы можно получить при старении сплавов Fe-Cu. Выделяющиеся при распаде мелкие частицы γ-Fe в этом случае удается сохранить при 0 К, и именно благодаря их исследованию стало известно, что при низких температурах γ-Fe является антиферромагнетиком с точкой Нееля 70 К и атомным магнитным моментом 0,6–0,8 µ_B [2–3].

Современные методы компьютерного моделирования, основанные на теории функционала плотности (DFT), позволяют с достаточной точностью описать энергию растворения и взаимодействие между атомами углерода в ферромагнитной фазе ОЦК-железа. При описании парамагнитного состояния железа, в котором локальные магнитные моменты разупорядочены, прямое использование расчетных методов DFT затруднено. Это связано с тем, что указанная теория использует зонную модель магнетизма и способна описывать лишь коллинеарные магнитные структуры кристаллов. В работе Окатова [4] проводилось моделирование парамагнитного состояния ОЦК и ГЦК-железа двумя способами: методом когерентного потенциала (DLM) [5] и на основе использования спин-спиральных (SS) [6] магнитных упорядочений с различными волновыми векторами q , вращение которых происходит вокруг направления бейновской деформации (001). Было получено, что в ГЦК-железе наиболее стабильными являются: антиферромагнитное однослойное АФМ1-состояние и состояние, полученное методом SS с q = 0,3. Энергию растворения углерода в различных магнитных фазах ГЦК-железа экспериментально определить довольно сложно [7–10]. Поэтому неоднократно совершались попытки её вычисления методами компьютерного моделирования [1, 11–13]. Однако в этих работах вычисления проводились только для упорядоченных коллинеарных магнитных состояний, тогда как реальное парамагнитное ГЦК-железо является магнитонеупорядоченным. В парамагнитном состоянии внутри объёма кристалла вследствие теплового движения атомных моментов могут возникать различные локальные магнитные структуры (локальные флуктуации магнитного порядка). Если атом углерода попада-

Ридный Я.М., Мирзоев А.А., Примеси углерода в парамагнитном ГЦК-железе: Мирзаев Д.А. ab initio моделирование энергетических параметров ет в области с различным магнитным порядком, он может обладать различной энергией растворения, а средняя энергия по сплаву будет представлять собой усреднённое значение по таким локальным параметрам. Впервые энергия растворения углерода в парамагнитном состоянии γ-железа была рассчитана в работе [14], где было показано, что адекватное описание магнитного состояния существенно влияет на результаты расчета. Однако в указанной работе не было изучено влияние парамагнетизма на энергию взаимодействия между атомами углерода, растворёнными в ГЦК-железе. Как хорошо известно, взаимодействие между атомами углерода определяет степень упорядочения в расположении углерода и влияет на характер γ→α превращения в сталях. К сожалению, экспериментальное изучение данного взаимодействия в ГЦК-железе довольно затруднительно [7, 15–23], потому что возможна только качественная оценка результатов. Попытки вычисления данных энергий методами компьютерного моделирования проводились в работах [11, 24–25]. В работах [24–25] моделирование ГЦК-железа проводилось в немагнитном (НМ) состоянии, которое никак не учитывает магнитные эффекты. В [14] моделирование проводилось в антиферромагнитном двухслойном (АФМД) состоянии. Это состояние было рассмотрено в нашей предыдущей работе [26], в которой было показано, что АФМД-состояние описывает парамагнитное ГЦК-железо недостаточно точно. Поэтому в настоящей работе представлены результаты расчетов энергии растворения примесей углерода и их взаимодействия между собой в парамагнитном γ-Fe.

Методика расчетов

В данной работе предложен метод моделирования парамагнитного состояния. Расчёты проводились из первых принципов полнопотенциальным методом LAPW, с учетом обобщенного градиентного приближения PBE-GGA в программном пакете WIEN2k [27], обеспечивающим высокую точность расчета полной энергии при минимальном количестве подгоночных параметров. Это наиболее точные методы, используемые в рамках теории функционала плотности DFT [28]. При интегрировании в обратном пространстве и вычислении электронной плотности использовалась схема Монхорста-Пака [29] с сеткой 4 х 4 х 4 к -точек зоны Бриллюэна для оптимизации геометрических параметров, и с сеткой из 7 х 7 х 7 k-точек для обеспечения точности расчёта в 1 мРб. Расчёты проводились при следующих значениях параметров моделирования [30]: параметр сходимости Kmax = 5 a.е.^–1, радиусы MT-сфер Rmt(Fe) = 2,00 a.е., Rmt(С) = 1,20 a.е. Критерием сходимости во всех расчётах было достижение точности расчета полной энергии системы, заряда и силы взаимодействия между двумя атомами не менее 10^–4 Рб, 10^–3 е и 1 мРб/а.е. соответственно.

Температурный диапазон существования ГЦК-железа лежит выше 1000 К, но особенности программного пакета WIEN2k позволяют провести моделирование только основного состояния системы при 0 К. При объёмной минимизации по энергии нами было получено, что происходит образование упорядоченных магнитных структур, которые никак не могут учесть локальные флуктуации магнитного порядка и которые дают недостаточно точные результаты при вычислении энергии растворения углерода. Поэтому для моделирования использовались равновесные параметры решётки, взятые из экспериментальной работы Онинка [31] для Т = 1400 К: а = 3,667 Å – для чистого ГЦК-Fe, а = 3,687 Å – для системы из 32 атомов железа и растворённого атома углерода и а = 3,707 Å – для системы из 32 атомов железа и двух растворённых атомов углерода.

Для определения энергии растворения углерода относительно фазы графита использовалась формула:

АН = E(Fe32 C) - E(Fe32) - E(C), где E(Fe32C) – энергии отрелаксированной суперячейки, состоящей из 32 атомов железа и одного атома углерода, находящегося в октапоре, E(Fe32) – энергия суперячейки, состоящей из 32 атомов железа, а E(C) – энергия одного атома углерода в решётке графита. Параметры структуры графита были взяты из работы Джианг [1] (a = 2,462 Å, c = 6,656 Å, α = 90°, β = 90°, γ = 120°).

Для нахождения энергии взаимодействия между атомами углерода из энергии системы с двумя атомами углерода вычитается энергия двух суперячеек, содержащих одиночные атомы углерода, и суммируется с энергией беспримесной суперячейки ГЦК железа:

АV = E(Fe32C2) - 2E(Fe32C) + E^32), где E(Fe32C2) – энергия релаксированной суперячейки, состоящей из 32 атомов железа и двух атомов углерода, находящихся в октапорах.

Моделирование магнитных конфигураций парамагнетика

Различные неэквивалентные магнитные конфигурации были получены с помощью программы BINAR [32]. В основе алгоритма программы BINAR лежит анализ степени неупорядоченности множества случайных конфигураций, полученных «вбрасыванием» атомов железа со спином вверх в подрешетку атомов железа со спином вниз с использованием генератора случайных чи- сел (в нашей суперячейке из 32 атомов – 16 атомов со спином вверх и 16 со спином вниз). После этого производится отбраковка конфигураций, не соответствующих критерию неупорядоченности. В качестве такого критерия используется величина суммы квадратов отклонений числа разнородных пар атомов (первый сорт атомов - атомы железа со спином вверх, второй сорт - атомы железа со спином вниз) во второй координационной сфере для рассматриваемой конфигурации от статистических средних значений для полностью неупорядоченной бинарной смеси (критерий согласия Пирсона χ2). В результате определялись магнитные конфигурации, в наибольшей степени соответствующие неупорядоченной ориентации атомных магнитных моментов по узлам суперячейки, и обеспечивающие равенство нулю полного магнитного момента ячейки.

В данной работе, как и в предыдущей [33], с помощью

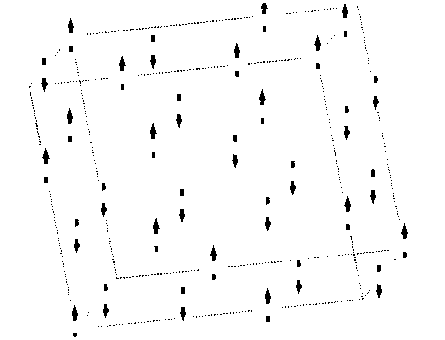
Рис. 1. Магнитная конфигурация супер-ячейки из 32 атомов железа, использованная для моделирования парамагнитного состояния в ГЦК-железе, обладающая наименьшей энергией. Стрелочками показаны спины атомов железа.

программы BINAR были получены 16 различных неэквивалентных магнитных конфигураций. По известной разности полной энергии n-ой конфигурации системы и энергии системы в наиниз-шем, основном состоянии (рис. 1), была вычислена каноническая статсумма (S):

S = £exp(-(En - E0)/kT) , n=1

где E 0 – энергия основного состояния, а E n – энергия системы в n -ом энергетическом состоянии; k – коэффициент Больцмана, Т = 1400 К (средняя температура существования ГЦК-фазы железа).

Из отношения вклада в статсумму от данной конфигурации (Sn) к всей статсумме была вы- числена вероятность существования магнитного состояния:

P = S

nS

e - ( E_n - E 0 )/ kT

S

Это позволяет вычислить усредненное по магнитным конфигурациям значение полной энергии су-перячейки ГЦК-матрицы железа, содержащей один или два внедренных атома углерода по формуле:

(E ) = X E „ P „ . n

Для расчётов выбирались 5 лежащих ниже остальных по энергии магнитных конфигураций (рис. 2). Вероятность существования остальных конфигураций была меньше 3 %, и их учёт не повлиял на конечные результаты, поэтому с целью оптимизации расчётов, в дальнейшем их не учитывали. Для

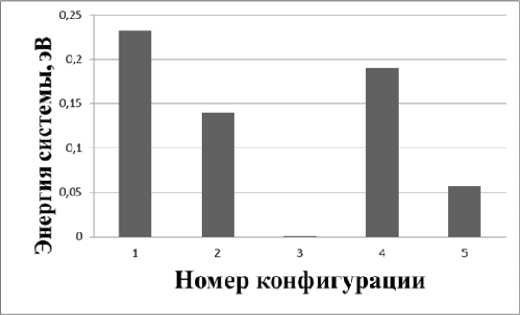
Рис. 2. График зависимости энергии системы от номера конфигурации. Энергии систем взяты относительно энергии самой низкой конфигурации

тестирования методики был проведен расчет энергии растворения углерода в парамагнитном состоянии ГЦК-железа, величина которой оказалась равной 0,25±0,03 эВ.

Полученное значение энергии растворения углерода в ГЦК-железе близко к экспериментальному и лучше согласуется с ним, чем результат, полученный в работе [14]. Это говорит о работоспособности выбранного нами метода и возможности моделирования им других энергетических характеристик. Интересно отметить, что при растворении углерод расталкивает ближайшие атомы железа не равномерно, а в зависимости от магнитной конфигурации, но в среднем на 5,1 %. Это меньше, чем при растворении в немагнитном (НМ) – 7,5 % и антиферромагнитном двух-

Ридный Я.М., Мирзоев А.А., Примеси углерода в парамагнитном ГЦК-железе: Мирзаев Д.А. ab initio моделирование энергетических параметров слойном (АФМД) – 6,5 % состояниях [30]. Атом углерода расталкивает атомы железа в первых двух координационных сферах [14] и изменяет их магнитные моменты. Сравнение наших данных для магнитных моментов и искажений решётки атомов ГЦК-железа в первых двух координационных сферах от атома углерода с данными Пономарёвой [14] проведено в табл. 1.

Таблица 1

Магнитные моменты и искажения решётки атомов ГЦК-железа в первых двух координационных сферах от атома углерода.

Координационная сфера	Искажение решётки, %		Магнитный момент атомов железа, µ B
	Данная работа	[14]	Данная работа	[14]
1	5,1	5,7	1,85	1,66
2	1	1,2	2,29	2,22

Из табл. 1 видно качественное согласие наших результатов с данными работы [14]. Внедренный атом углерода уменьшает магнитный момент атомов железа в первой координационной сфере и увеличивает во-второй.

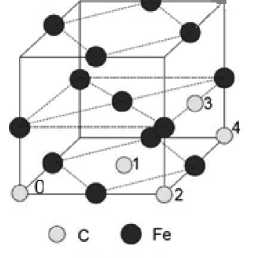
Рис. 3. Возможные расположения атомов углерода в супер-ячейке из 32 атомов железа. Атомы железа чёрным цветом, а углерода светлым. Отчёт идёт от атома номер ноль

Энергии взаимодействия между атомами углерода в ГЦК-железе можно вычислить экспериментально [7, 15–23] для первых двух координационных сфер (рис. 3). Наиболее точные значения энергий взаимодействия между атомами углерода в ГЦК-железе получены на основе моделирования методом Монте-Карло мёссбауэровских спектров ГЦК сплавов Fe-C [15–18]. В то же время, многочисленные термодинамические расчеты [7, 19–23], основанные на различных модельных представлениях о взаимодействии между атомами углерода, приводят к сильно отличающимся результатам. Все указанные литературные данные о значениях энергии взаимодействия между атомами углерода, а также результаты, полученные в данной работе, представлены в табл. 2.

Таблица 2

Энергии взаимодействия между атомами углерода в ГЦК-железе, эВ

Номер коор. сферы	1	2	3	4
Мёссбауэр. спектр. [15–18]	0,036–0,115	0,075–0,169	–	–
Термодинамический эксп. [7, 19–23]	0,065–1,55	–	–	–
Данная работа	0,06	0,2	0,01	0,05

Из табл. 2 видно, что наиболее сильно отталкивают друг друга атомы углерода, располагающиеся во второй координационной сфере друг относительно друга. Значительно слабее отталкивание между атомами С в первой и особенно в третьей, координационной сфере. Достоверность полученного результата подтверждает качественное согласие с данными мёссбауэровской спектроскопии.

Заключение

• 1.    Предложена методика усреднения результатов моделирования по наинизшим по энергии магнитным конфигурациям, наиболее близким к парамагнитному беспорядку. Энергия растворения углерода в парамагнитном состоянии γ-Fe составила 0,25±0,03 эВ. Данное значение энергии неплохо совпадает с экспериментальными результатами, что говорит о работоспособности методики.

• 2.    Показано, что после внедрения в решётку парамагнитного γ-железа атом углерода раздвигает ближайшие атомы железа в среднем на 5,1 %, что меньше, чем при растворении в немагнитном (7,5 % ) и АФМД (6,5 % ) состояниях железа.

• 3.    При растворении углерода в ГЦК решетке железа происходит снижение среднего магнитного момента на атом железа в первой координационной сфере и увеличение во второй.

• 4.    Проведен расчет зависимости энергии взаимодействия между атомами углерода от расстояния между ними в парамагнитном состоянии ГЦК-железа. Показано, что взаимодействие

• 5.    Полученные нами значения энергии взаимодействия между атомами углерода существенно отличаются от значений энергии полученных в большинстве термодинамических расчетов.

между атомами углерода носит отталкивающий характер, причем оно максимально во второй, а минимально в третьей координационной сфере.