Принцип длинных волн и фононные спектры кубических кристаллических решёток

Настоящая работа представляет собой продолжение исследований, начатых в [1], где была построена динамическая модель для ОЦК и ГЦК кристаллических решеток, использующая силы межатомного взаимодействия, имеющие ван-дер-ваальсовскую природу, и произведены расчеты дисперсионных кривых для Na и Al. Согласно принципам, сформулированным в [1], атом кристалла рассматривается как структуризованный объект, состоящий из ионного остова и электронов на внешних оболочках. Считается, что остов колеблется как единое целое, а колебания электронов на внешних оболочках сводятся к колебаниям их центра заряда. Положение центра заряда внешних электронных оболочек (в.э.о.) определяется взаимным расположением остова рассматриваемого атома A и остовов его соседей, находящихся на первой и второй координационных сферах атома A , и не обязано совпадать с положением его остова. В результате внутри атома наводится дипольный момент, действующий с некоторой силой на его остов. На остов атома действуют силы излучения диполей остальных атомов решетки, которые, изменяя положение центра заряда в.э.о., наводят в атоме A дополнительный дипольный момент, частично экранирующий эти силы. Атом A , представляющий собой динамический диполь, излучает электромагнитную энергию. Эту энергию можно рассматривать как работу силы реакции на излучение, которая, как это можно показать [2], в первом приближении пропорциональна плечу диполя. В состоянии термодинамического равновесия, когда на любом временном промежутке энергия, поглощаемая атомом, совпадает с энергией, излучаемой им, внешняя, частично экранированная кулоновская сила уравновешивается силой реакции. В результате движение остова атома происходит под действием силы внутреннего диполя, наведенного соседними атомами и имеющего квантовомеханическую природу своего возникновения.

Принцип длинных волн

Рассмотрим моноатомную кристаллическую решетку и обозначим через µ – массу остова каждого ее атома, через q – его заряд и пусть β = q ² / 4 πε ₀ .

Пусть Λ - какое-нибудь множество индексов, с помощью которого можно занумеровать все атомы решетки. Для каждого xn L обозначим через A _ξ соответствующий атом решетки, через P _ξ – узел, являющийся положением равновесия атома A _ξ , а через u _ξ – смещение остова атома A _ξ из положения равновесия в некоторый момент времени t . Обозначим, далее, через S_l ( ξ ) - множество индексов из Λ , нумерующих атомы решетки, находящиеся на l -й координационной сфере атома A _ξ . Пусть A _{ξ ′} - атом, соседний с атомом A _ξ . Перемещение остовов атомов A _ξ и A _{ξ ′} относительно друг друга вызывает изменение степени перекрытия орбиталей их в. э. о., что при-

Физика

водит к возникновению у этих атомов соответствующих дипольных моментов. Будем считать, что перекрытие орбиталей может происходить у атомов, лежащих друг относительно друга на первой и второй координационных сферах. Причем для атомов, лежащих друг относительно друга на первой координационной сфере изменение степени перекрытия орбиталей будет происходить как при радиальном, так и при тангенциальном (вращательном) перемещении их друг относительно друга. Для атомов же, лежащих друг относительно друга на второй координационной сфере, изменением степени перекрытия их орбиталей при тангенциальном перемещении мы будем пренебрегать. Обозначим через е ^ единичный направляющий вектор вектора Р ^ Р ^ , а через w ^c ' = И с - И с - вектор относительного перемещения остовов атомов а ^ и А с . Пусть r ^ = е сс <  е сс ’’ w с с >  — радиальная, а т ^ = w^ — Г сс — тангенциальная составляющие вектора w^ =- ^W CC ' , где в скобках обозначено скалярное произведение векторов е сс и W cc ' . Тогда плечо дипольного момента р ^ , наведенного в атоме А с со стороны атома А ^, лежащего на его первой и второй координационной сферах соответственно, можно определить формулами:

^р сс = ^K ir ^г сс + ^K i t ^т сс = ^{( к} 1 r ^{- K} i t ) <  ^е сс , w s? >  ^е сс + ^К 1 1 w S? ’                       ⁽¹⁾

^р сс = ^к 2 r <  ^е сс , ^№ сс >  ^е сс ’                                        ⁽²⁾

где к 1 _r , к 1_t , к _{2 r} - числовые параметры, постоянные для данного кристалла.

Плечо Р с полного дипольного момента, наведенного в атоме А с со стороны всех его соседей, вычисляется путем суммирования по всем соседним атомам из первой и второй координационных сфер

Р с = 2 Р с ⁺ 2 Р сс '.                              ⁽³⁾

с е S , ( с )         с 'е S 2 ( с )

С учетом сказанного выше, в состоянии термодинамического равновесия уравнение движения остова атома принимает вид

Ц && с = В с =- ^^в Р с ,                                      ⁽⁴⁾

где a - поляризуемость атома.

Пусть рассматриваемый кристалл имеет ОЦК или ГЦК кристаллическую решетку. Будем считать, что он имеет форму куба, содержащего n ³ элементарных кубических ячеек, и обозначим через а параметр решетки. Положим N = {1,2,...,2 n }. Зададим в пространстве систему кристаллографических координат Oxyz с единичными направляющими векторами е x , е _у , e _z координатных осей так, чтобы положение каждого узла Р = P ijk решетки могло быть задано по формуле

°^Р ук = I^{( i e} x ⁺ j ^e у ^{+ к е} z ) ,                                  ⁽⁵⁾

где i , j , к е N - некоторый набор чисел. Обозначим через Л подмножество в N ³ , образованное такими наборами ( i , j , к ), для которых формула (5) определяет узел решетки. Тогда для ОЦК решетки

Л = {( i , j , к ) е N ³ | i , j , к - все нечетные или все четные числа }, а для ГЦК решетки

Л = {( i , j , к ) е N ³ | сумма i + j + к нечетна }.

Подставляя (1), (2) в (4), полагая 0 -1 _r = рк , _r / a , ° 1 t = вк 1 t / a , а ₂ r = вк _{2 r}/a и занося знак « - » под знак суммы, приходим к уравнению

M u с = 2 1 ⁽ ^ | r ^- °' 1 ) <  ^е сс , w cc ' >  ^е сс ⁺ ° 1 w cc '] ⁺ 2 ° 2 r <  ^е сс, w cc ' ^{> e} cc ' .            ⁽⁶⁾

с' е S 1 ( с )                                                                          с' е S 2 ( с )

Пусть с = ( i , j , к ) еЛ и с ' = ( i ', j \ к ') е S i ( с ), l = 1,2. Положим e ii. = i' - i , £ _у = j' - j , ^е _кк' = к' - к , p l = ^ g i ². + £ 2 + £ 2. . Тогда вектор е сс , указывающий направление от узла Р с к узлу

^. x = Е ^{ ° ¹ r^S“ ‘ ^{+ ( Р} 2 ^e ii ‘ ) ° 1t w® . x ^{+ £} ii' ^{( e} Vw^y ^{+ £} kk' w ^, z ^{)} +} E ° 2        • ⁽⁷⁾

Г ’ e $ 1 ( Г )                   ^P 1                                                                               Г ’ e $ 2 ( Г )

Введем обозначения:

r = Op , A r = Pp . , ^u x ⁽ r , t ) = n , x , u x ⁽ r + ^A r , t ) = ^u ^ , x .

Функция ux (r, t) выражает проекцию на ось Ox отклонения остова атома А^ в момент вре мени t из положения равновесия Р^ , радиус-вектор которого равен r . Если считать, что она опи сывает колебания решетки длин волн много больших ее параметра, то при изменении аргумента на величину порядка а она ведет себя как, по крайней мере, дважды дифференцируемая функция. Следовательно, для вычисления ее приращения при переходе в соседний узел решетки можно воспользоваться формулой Тейлора до дифференциалов второго порядка. Считая момент времени t постоянным и опуская его в обозначениях, получим w«', x = Ux (r + Ar) - Ux (r) = VUx Ar + 2 < Ar, (V' Ux )Ar > ’

где V u_x - градиент функции u_x , а ( V 'u_x ) - матрица, строки которой соответственно равны:

∂u    ∂u    ∂u

V —-, V —-, V —- .

∂x    ∂y    ∂z

Для произвольного узла решетки, положение которого определяется вектором r , вектор Ar смещения в положение соседнего узла равен a r=a r$ = 2 (e7 ex+£jj' ey+ekk■ ez), где eii., e^ , ekk определяются так же, как и выше. Подставляя Ar в выражение , приходим к равенству

= a^{e2,

+ ^{2 e} ii ' e

a ² u _x

9x2

92 u.

kk ' О О

9x9z

₂ 9 ² u ₂ 9 ² u           9 ² u

Ь e1    x- + ekk, —p + 2eii,e j,----— + jj 9y         9z2      “ jj 9x9y

+ 2e.,e ,-9-u2L}.

jj ^kk 9y9 z^

Пусть, как и выше,   Г = ( i , j , k ) eЛ и Г = ( i' , j ‘ , k 3 e S l ( Г ),   l = 1,2.  Обозначим через

Г e Sl (Г) индекс атома, соседнего к  А^, расположенного противоположно атому А^. Пусть далее Sl(Г) - набор индексов какой-нибудь полусферы l-й координационной сферы атома А^. Тогда, например,

Е w rr , x = Е ⁽ w rr , x ⁺ w r , x ), r' e S l ( r )                r ’ e $ l ( r )

при этом согласно (8)

wrr, x + wr, x = ux ( r + A rrr) + ux ( r -A rrr) - 2 ux (r) = < Arr,(V ^xx )A rr > .      (10)

Переходя в формуле (7) к суммированию по полусферам, заменяя при этом w^^ x на w==. x + w x, и т.д., в случае ОЦК решетки приходим к уравнению , rr ,x d2ux   a2                       . d2ux                  d2ux d2ux                   d2uy d2u p     = — {(°1 r + 2°11 + 3° 2 r ) ^7^ + (°1 r + 2°11)(+ ^7^) + 2(°1 r - °11 )(^^ +     ИХ11)

d t ²     3                        d x ²                  d y ²     d z ²                   d x d y d x d z

Соответствующее уравнение в случае ГЦК решетки имеет вид

Физика

µ

д ² u x дt²

= aT^{2 ^ r

„    x д² u_{r z            x/}d² u_x д ² u_rx                  5² u y д ² u_7x,

- ^CT 1 t ^{+ 2} ^ 2 r ) TT ⁺ ( ^CT 1 r - ³ ^ 1 t )( ^"T ⁺ , - ) ^{+ 2}( ^ 1 r ^{+ CT} 1 t )(^^ ⁺       )} "( ¹² )

д x ²                 d y ²     д z ²                  д x д y д x д z

Согласно принципу длинных волн [3] уравнения (11), (12) должны переходить в классиче

ские уравнения распространения упругих волн деформаций в кристаллах. В проекциях на ось Ox

для ОЦК и ГЦК решеток эти уравнения соответственно имеют вид [4]:

д2ux   2,аС„ д2U ц —= а 2(—- —x-д t2          2 дx2

aC₄₄ д² u_x + —— (—+

2     д у²

д ² U x ) + а ( C ,2 + C 44 ) ₍ ^{д 2} u y + д ² u_z ) , д z²          2       д x д y   д x д z

^{д 2} u x = a 2₍ ^aC 11 ^ Ч + ^aC 44 ₍ ^Х + дХ ) + a ^{( C} 12 ^{+ C} 44 ) ₍ ⁵ 2 ^Uy + ^д 2 ^Uz )

^ц д t ²        4   д x ²     4   Ч y ² д z 4 д x д y д x д z

где C it , C 12 , C ₄₄ - упругие константы рассматриваемого вещества.

Сравнивая уравнения (11) и (12) соответственно c (13) и (14), приходим к соотношениям между коэффициентами динамической модели и упругими константами.

В случае ОЦК решетки

^1 r = 2 (C12 + 2 C44), ^11 =   C 44 - C12) , CT 2 r =   (C11 " C44)"(

В случае ГЦК решетки

CT1r = 2T(3C 12 + 5C44 ) ’ CT11 = ~ (C44 - C12) , CT2r = “(2C11 - C12 - 3C44 ) "

о                       00

Расчет фононного спектра

Будем искать решение уравнения (4) в виде бегущих волн, заданных формулой u(r, t) = sin(Kr - tot)g, (или u(r, t) = cos(Kr - tot)g), где g = gxex + gyey + gzez - единичный вектор, указывающий направление поляризации волны, a                 а                                       2п2

r = —(iex + jey + kez) = —^ - радиус-вектор узла решетки, а K = —(kxex + k ey + kzez) = —k-

2 y 2                                         na                     na волновой вектор. При этом для того, чтобы были выполнены условия цикличности Борна-Кармана, можно считать, что kx,ky,kz = 0,...,n -1. Поскольку скалярное произведение Kr определяет фазу колебаний, плоскости постоянной фазы задаются уравнением k^ = kxi + kyj + kzk = m, где m - натуральное число, постоянное для данной плоскости, которую мы обозначим Qm . Колебания любых двух атомов А^ и А^., узлы которых находятся на плоскости Qm , совпадают и задаются формулой

π m

U $ = ^M f = U m ( t ) g = Sin(-- to t ) g .

n

u §' = ^U m' ^g , w cc = ^{( U} m ^{- U} m' ) ^g , e CC = ⁶ CC / ^P l .

Для каждого атома A^, соседнего атому А^, обозначим через m' - номер плоскости, на которой находится атом А^ . Тогда 6^^ = -£cc, m ' = m - d^^ . Положим н J                  j j .                                                 fl81

m , d m m m - d - d m + d + d .

Подставляя (17) в (10), получим

π d

^Umd = ^{4 u}+ ^sin — .                                      ⁽¹⁹⁾

2 n

Пусть g ; =< г ;; , g > , к ₁ = ^{K 1} r _^{K 1} t , ст ₁ = рк ₁/ a . Тогда с учетом введенных обозначений и P 1

формул (1), (2) и (19) приходим к равенствам:

2 n d ее '

Р ее ⁺ Р ;е■ = ⁴ u m ^sin "2П" ^к g eeЧе ^{+ К} 1 1 g ),                         ⁽²⁰⁾

^{n d} ;e

Р ;е ⁺ Р ;е = ^к 2 r u m ^sin -2^- g ;e ^г ее -                             ⁽²¹⁾

Пусть ; = ( i , j , k ) еЛ , а S l ( ; ) - какая-нибудь полусфера координационной сферы S l ( ; ), l = 1,2 . Тогда

Е Р ; = Е ⁽ Р ;г ⁺ Р ; ),

;' е Sl ( е )           ; - е s_t ( е )

а формула (3) представляется в виде

Ре = um{4 Еsin2"Г"(к1 g;г;+ к18)+ к2r Е sin2"dr"g;г;;,}-(22)

; е S 1(;)      2 n                                   ; е s 2()

Подставляя (17) в уравнение (4) и учитывая полученную выше формулу и определенные ранее коэффициенты ст _{1 r} , ст _{1 1} , ст _{2 r} , ст ₁ , приходим к уравнению

2            2 ^{n d} ee 2

Ц»д = 4 Е sm < |CTigee4e + CT1g)+ст2r Esin ^S;8;’

; е s1(;)       2 n                             ее s2<е)

которое распадается на систему уравнений в проекциях на координатные оси следующего вида: axgx + bzgy + bygz = ^gx , bzgx + aygy + bxgz = Xgy , bygx + bxgy + azgz = Xgz , где X = цю2. После несложных преобразований система (24) приводится к системе cxgx - bzgy - bygz = (сто — X)gx ,

• -    bzgx + cygy - bxgz = (CT0 - X)gy ,

• ^-    b y g x ^- b x g y ⁺ c z g z = ^{( CT} 0 ^{- X} ) g z ,

в которой cx + cy + cz = 0 . Положим y = ст0 - X . Тогда характеристическое уравнение системы (25) принимает вид у3 + (cxc + c cz + cxcz - b2 - b2 - bz!)y + b2cx + b2c + bz2cz - cxc„cz + 2bxb b = 0.(26)

xy yz xz x y z     x x y y z z xyz xyz

Для сокращения записи при вычислении коэффициентов уравнения (26), положим

c ( k ) = cos ^{n k} , s ( k ) = sin ^{n k} . Тогда в случае ОЦК решетки:

nn

Cx = 3 ст 2 r (2 c (2 kx) - c (2 ky) - c (2 kz)), bx = J (ст1 r - CT11)c(kx )s(ky )s(kZ ) ,

CT0 = j(CT1 r + 2CT11 )(1 - c(kx )c(ky )c(kz )) + J CT2r (3 - c(2kx ) - c(2ky ) - c(2kz )) , а в случае ГЦК решетки:

cx = j(CT1 r - CT 11)(c(kx)c(ky) + c(kx)c(kz) - 2c(ky)c(kz)) + J CT2r (2c(2kx) - c(2ky) - c(2kz)), bx = 2(CT1 r -CT11)s(ky)s(kz),(28)

• 4 .                      .         .         .              .         .2

CT 0 = ₃( CT 1 r + 2 CT 1 1 )(3 - c ( k x ) c ( k y ) - c ( k y ) c ( k z ) - c ( k x ) c ( k z )) + ₃ ct 2 r (3 - c (2 k x ) - c (2 k y ) - c (2 k z )) ,

Физика

причем остальные коэффициенты вычисляются путем круговой перестановки индексов x , y , z .

С учетом формул (15), (16) равенства (27), (28) могут быть записаны так: в случае ОЦК решетки:

Cx = |(Cn - C44)(2c(2kx) - c(2ky) - c(2kz)), bx = 2 a (C12 + C44) c (kx) 5 (ky) 5 (kz),                                  (29)

а о = 4 aC 44 (1 - c (k x ) c (k y ) c (k_z )) + - a (C „ - C 44X 5 ²( k x ) + 5 ²( k y ) - 5 ²( k_z ));

в случае ГЦК решетки:

cx = Ц{4(C12 + C44)(c(kx)c(ky) + c(kx)c(kz)-2c(ky)c(kz)) + (2Cn -Cn -3C44X2c(2kx)-c(2ky)-c(2kz)} bx = a (C12 + C44) 5 (ky) 5 (kz),                                   (30)

а0 = 6{(C12 + 7C44)(3 - c( kx ) c( ky ) - c (ky ) c (kz ) - c (kx ) c (kz )) + (2Cn - C12 - 3C44)(52( kx ) - 52( ky ) - 52(kz )}, а остальные коэффициенты вычисляются путем перестановки индексов x, y,z .

Положим

• -    3 p = c_xc_v + c_vc_z + c_xc_z - b x - b 2 - b , xy yz xz x y z

• -    q = b 22 c_x + b 2 c + b _z ² c_z - c_xc_vc_z + 2 b_xb b_z , xx yy zz xyz xyz тогда уравнение (26) запишется в виде

Y3 -3pY -q = 0,(31)

а его решения выразятся формулой

Ym = 2д/p cos Ф + 32^ , m = 0, 1, 2, qπq где ф = arccos—или ф = — arctg—,.

2V p ^{3          2}        V⁴ P ³ - q ²

Тем самым частоты фононного спектра в ыражаются ф ормулой

® = 4(a 0 - Ym )/И •

Ниже, в табл. 1 и 2 приводятся значения исходных данных для ряда элементов, имеющих ОЦК и ГЦК решетки, на основе которых были произведены расчёты фононных спектров для Na и V при температуре 78 K, для Al и Cu при 0 K, представленных на рис. 1–4.

Таблица 1

Атомная масса µ , параметр решетки a , упругие константы C ij элементов с ОЦК

Вещество	µ , a.e.	a , Å	Т , К	С 11 , ГПа	С 12 , ГПа	С 44, ГПа
Na	22,9897	4,2906	78	8,2	6,8	5,8
			298	7,3	6,2	4,26
V	50,9414	3,0282	78	231,77	119,2	45,23
			298	228,00	119	42,60

Таблица 2

Атомная масса µ , параметр решетки a , упругие константы C ij элементов с ГЦК

Вещество	µ , a.e.	a , Å	Т , К	С 11 , ГПа	С 12 , ГПа	С 44, ГПа
Al	26,98	4,04959	0	122,6	70,8	30,6
			298	107,3	60,9	28,3
Cu	63,55	3,61479	0	176,2	124,9	81,7
			293	168,4	121,4	75,4

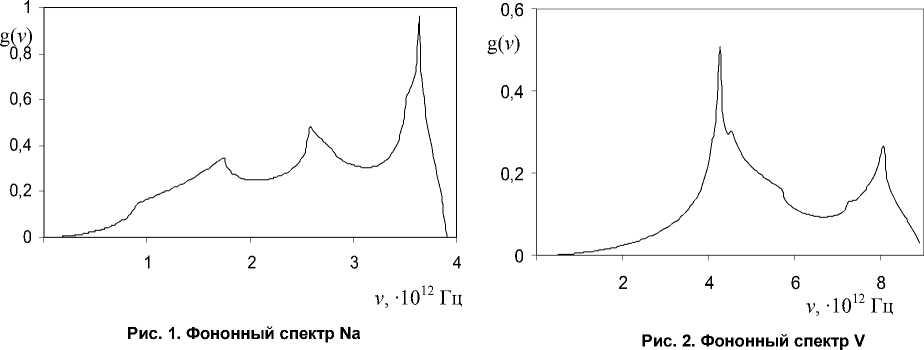
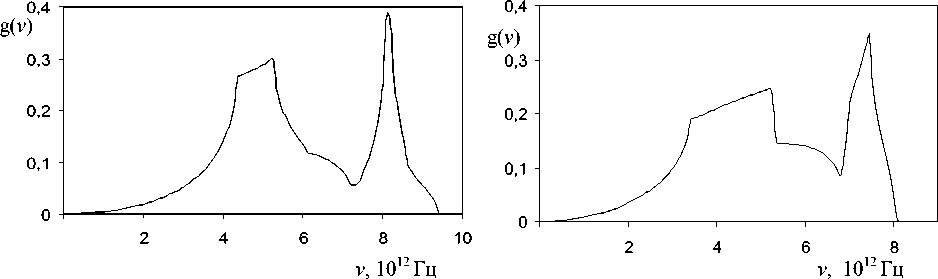
Рис. 4. Фононный спектр Cu

Рис. 3. Фононный спектр Al

Статья выполнена при поддержке программы ФА по образованию «Развитие научного потенциала высшей школы» (грант РНП 2.1.1.7071).