Принцип максимума для нагруженного уравнения гиперболо-параболического типа

Рассмотрим в области П, ограниченной отрезками AAo, BBo, Ao Bo прямык x = 0, x = l, y = h > 0 соответственно при y >  0, и характеристиками волнового уравнения AC : x + y = 0, BC : x — y = l при y <  0, характеристически нагруженное уравнение [1]

0= jLiu = uxx — Uy + aiUx + ci u + d¹u(x, 0),                             y> 0,

L2u ≡ uxx - uyy+ a2Ux + b2Uy + C2U + d2u(x + y, 0) + e2u(x — y, 0), y< 0, где u = u(x,y) — поизвестиая функция: ai = ai(x,y), ci = ci(x,y), di = di(x, y), i = 1, 2. b2 = b2(x,y), e2 = e2(x,y) — заданные непрерывные в области своего определения функции.

Обозначим через; П+, П- параболическую и пшербо.тнческуто части области П соответственно.

Принцип экстремума, играет важную ролв при исследовании задачи Трикоми для уравнений смешанного типа. Впервые принцип экстремума, для задачи Трикоми был сформулирован в 1950 г. А. В. Бицадзе [2] для уравнения, которое впоследствии получило название уравнения Лаврентвева. — Бицадзе. Дальнейшие исследования в этом направлении велись многими математиками, краткий обзор результатов приведен в работе [3].

В работах [4, 5] были сформулированы принципы экстремума, для нагруженных интегральных уравнений и дифференциального уравнения первого порядка. В [6, с. 264], [1, с. 126] доказан принцип максимума, для точечно нагруженного уравнения параболического типа, в работе [7] — принцип экстремума, для характеристически нагруженного уравнения гиперболического типа, второго порядка.

Полученные в данной работе результаты обобщают принцип максимума, для уравнения смешанного гиперболо-параболического типа, приведенный в [8, с. 10], и при d1 = d₂ = e₂ = 0 следствие 1 совпадает с вышеуказанным принципом максимума.

Кроме того, при d2 = e2 = 0 полученный принцип экстремума для нагруженного гиперболического уравнения совпадает с принципом экстремума Агмона — Ниренберга — Проттера, сформулированным для гиперболического уравнения в [6, с. 229], и условия леммы 1 согласуются с условиями, полученными в работе [9].

Докажем сначала принцип максимума для нагруженного гиперболического уравнения в Q-.

Уравнение (1) в Q^- в характеристичееких координатах £ = x + y. n = x — У имеет вид

V^n + pv^ + qvn + rv + Xv(£, £) + Цv(n, n) = 0,                    (2)

где 4p = a2 + 62, 4q = a2 — b₂, 4r = C2, 4X = d₂, 4ц = e2, v = v(£, n) = u(x, y), f< ^^- U AB перейдет в области D = {(£,n) : 0 < ^

Лемма 1. Пусть v(£,n) ~ регудяршэе в области D решение ;t 'равнения (2) и в C(D) удовлетворяющее условиям

Vn е C (0 6 ^ 6 l), Vn (0,n)+ p(0,n)v(0,n) 6 0.                (3)

Тогда, если p. p^. q. r. X н ц принадлежат C (0 6 £ < n 6 l), ri(€,n) 6 0, X(£,n) 6 0, ц(£, n) 6 0,                           (4)

piG^n) +

ξ

/ 0

[ r(£i ,n) + X(€i,n) + M^n)] qi(£i , n) d£i

> 0,

где r_i = rq_i — p-ц, p_i = pq_i, q_i = exp jj q(t, n) dt, то положительный максимум функции v(£,n) ^B D достигается то.тько па отрезке 0 6 £ = n 6 l-

C Доказательство леммы 1 проведем методом, предложенным в [6, с. 228]. Действительно. пусть (еД) — произвольным образом фшесированная топка, из области D. Если p в области D имеет непрерывную производную по ^, a q непрерывна, в D, то уравнение (2) в классе функций v = v(^,n), имеющих в D первые и вторые смешанные производные, эквивалентно уравнению

(qi vn + piv)₅ + rpv + Xiv(^, 0 + mv(n, n) = 0

или нагруженному уравнению первого порядка.

qi⁽^,n^)vn ⁽^n) ⁺ pi^nM^n) ⁺

ξ

У ri(^i,n)v(^i,n) d^i

ε

= qi⁽E,n)^vn ^(e,n) ⁺ pi⁽E^,n^)v(E^,n^{) —}

ξ

У ^Xi⁽€i,n^)v(€i ,€i) d^i ε

ξ

У М^дпМтй) d^i, ε

где Xi = Xqi. щ = pqi- 0 <^

Перепишем (6) в следующем виде:

ξ qi(€,n)vn(£>n) = J H£,n)

ε

- vC^n)] ri(£i, n) d£i + qiOcn) [vn(e,n) + pOcnWcn)]

ξ

⁺ J H^n)

ε

ξ

- ^v(£i^,£i)] Ai⁽^i,n) d^£i ⁺ J [v(^£,n)

ε

- v(n,n)] Pi^(£i^,n) ^d£i

+

- v^(£,n)

pi(£,n) +

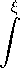
ε

[rinkite, n) ⁺ Ai(^£i ,n) ⁺ №^(£i,n)] d^£i

ξ j [v(£, n) - v(£i, n)] ri(£i, n) d£i + qi(E, n) [vn(C n) + P(C n)v(C n)] ε

ξ

ξ

j H^n) - ^v(£i^,£i)] АДф^) d^£i ⁺ j H^n)

- v(n,n)] ^i(£i>n) d£i

ε

ε

ξ

- v^n) piM + / [rG^nH A(^i,n) ⁺ M^n)] qi^(£i^,n⁾ d^£i •

Допустим теперь, что положительный максимум функции v(£,n), являющейся регулярным решением уравнения (2), в D достигается в точке ( £ о ,П о) , 0 < £о < no 6 l. Из (7) при £ = £о- n = П о ,^е ^ 0, имеем

ξ0

qi^, П о ^)vn^(£о ,П о) = j Н^По )

^- « (^£п п о)] ^г1⁽€1,по) d€i

+

ξ0

j [v⁽&,По)

- v(€i,€i)] Ai(^i,по) d€i +

ξ0

j Н£о,по)

^{- v(}no ,по) №⁽6.,По) d€i

ξ

- v(€o,no)

Р1(€о ,по) +

/

[^г(€1,по) ⁺ А⁽^1,по) ⁺ рХАъпо )] q1⁽^1,no) d^i

+ qi (0, n) [vn (0, n) + p(0, n)v(0, n)] •

Из (8), учитывая, что qi(^,n) > 0, и условия (3)-(5), получаем, что Vn(^о,По) < 0. Но это противоречит сделанному допущению, так как в точке (^о, По) положительного максимума v_n(^о, П о ) > 0. Следовательно, положительный максимум (рупкщш v(^,n) в D достигается только на отрезке 0 6 ^ = n 6 l- B

Аналогично доказывается, что при замене условия (3) леммы 1 на условие

Vn G C(0 6 £ < n 6 l), Vn(0,n) + p(0,n)v(0,n) > 0, отрицательный минимум функции v(£, n) в D достигается только на отрезке 0 6 £ = n 6 l.

В параболической части П+ смешанной области П справедлива следующая лемма.

Лемма 2. Пусть u(x,y) — регулярное в Q+ решение i равнения (1) и в C (Л+). удовлетворяющее условию Liu > 0 (6 0). ai(x,y),ci (x,y),di (x,y) Е Q+ п ci(x,y) + di(x,y) < 0, di(x,y) > 0.                            (9)

Тогда положительный максимум (отрицательный минимум) функции u(x, у) в Q может постигается только па AAo, AB, BBo.

<1 Доказательство леммы 2 проведем аналогично [6, с. 263]. Достаточно доказать лемму 2 для случая положительного максимума, так как случай отрицательного минимума сводится к нему заменой u iia —u. Пусть решение u уравнения Liu = 0 достигает положительного максимума, в топке (xo, yo) Е Q+. Необходимое условие максимума, функции ив точке (xo, yo) имеет следующий вид: ux = 0, uy = 0, uxx 6 0. Принимая это во внимание, из (1) находим ci(xo ,yo)u(xo ,yo) + di (xo,yo)u(xo, 0) = — Uxx(xo,yo) > 0.

С другой стороны, с учетом (9), получим ci(xo ,yo)u(xo , yo) + di (xo,yo)u(xo, 0) = ci(xo,yo )u(xo , yo) + di(xo ,yo)u(xo, 0) + di(xo,yo)u(xo,yo) - di(xo,yo)u(xo, yo)

= [ci(xo,yo)+ di (xo,yo)]u(xo, yo) - di (xo,yo)[u(xo, yo) - u(xo, 0)] < 0.

Полученное противоречие — результат неверного допущения, и (xo, yo) Е Q+- Утверждение, что точка максимума не принадлежит AoBo, доказывается также, как и в случае, когда yo < h, но с той лишь разницей, что необходимое условие экстремума uy(xo,yo) = 0 щш yo < h заменяется условием uy(xo,yo) > 0 щ>n yo = h.

Отмстим, что замена u = vexp(ay), где постоянная a > 0, приводит к уравнению вида. Liv = 0 с коэффнщшитом при v. равным ci — a. и коэффициентом при v(x, 0). равным di exp(—ay). Если <]>упкщш ci 11 di непрерывны в замыкашш Q. то при достаточно больших a этот коэффициент при v строго отрицателен. кроме того, можно подобрать a таким образом, чтобы выполнялось ci(x,y) — a + di(x, y) exp(—ay) < 0. B

Для уравнения (1) имеет место следующий принцип максимума.

Теорема 1. Пусть

• 1)    u(x,y) Е C(Q)nCⁱ(Q)nC2(Q-)nCX(Q⁺). u(x,y) удовлетворявт неравенству L_iu > 0 в Q⁺, ii L2u 6 0 в Q^-б кроме того, функция u(x,y)|Ac = 0 и обладает свойством

  ^∂-^∂

  ∂y ∂x

  
  

u Е C(Л" \ AB);

• 2)    в Q коэффициенты a₂, b₂ Е Cⁱ(Q ), c₂, d₂, e₂ Е C(Q ), и удовлетворяют условиям леммы 1;

• 3)    в Q коэффициента! a_i, c_i, d_i непрерывны ii удовлетв оря ют условиям леммы 2.

Тогда (функция u(x, y) свой положитедвив1Й максимум в Q принимает на отрезках AA_o 11 BB_o.

• <    Из леммы 1 следует. что (]>упкция u(x,y) свой положительный максимум в Q принимает в точке (xo, 0) отрезка AB, причем в точке положительного максимума

V(xo) > 0,                                           (10)

где v (x) = uy(x, 0).

В Q из леммы 1 и леммы 2 при выполнении условий теоремы 1 следует, что положительный максимум функции и(х,у) может достигаться только на отрезках AAo, BBo. AB. Покажем теперь, что для функции u(x,y) любая внутренняя тонка (хо, 0) отрезка AB не может быть точкой положительного максимума. В самом деле, в силу непрерывности производных u_x, u_y , u_xx из перавенства L1u >  0 мы можем перейти к пределу при у ^ +0

т ⁰⁰(х) + a1(x, 0)т⁰ (х) + [ci(х, 0) + d₁(x, 0)]т(х) — v(х) > 0,               (11)

где т (х) = и(х, 0). Из (11) в силу условий (9) леммы 2 в точке положительного максимума имеем v(хо) < 0, что противоречит неравенству (10). откуда следует, что функция и(х,у) не может достигать положительного максимума во внутренней точке (хо, 0) отрезка AB. Таким образом, при выполнении условий теоремы 1 положительный максимум функ-щш и(х,у) может достигаться только на отрезках AAo ¹¹ BBo- ^{что 11} требовалось доказать. B

Из теоремы 1 легко получить

Следствие 1. Пусть

• 1)    выполнены условия 1) теоремы 1;

• 2)    в Q+ коэффс пшепты a1. c1. d1 непрерывны и выполпяются условия (9);

• 3)    в И коэффициенты a₂,b₂ G C 1(Q ), c₂,d₂ , e₂ G C (Q ), п выполняются условия

a2 — b2 + 2a2x + 2b_2x + 2a₂y + 2b₂y — 4c2 > 0,                    (12)

a2 + b2 > 0, C2 + d2 + e2 > 0, d2 6 0, e2 6 0.                  (13)

Тогда функция и(х, у) свой положительный максимум в Q принимает на отрезках AA₀ 11 BB₀.

Действительно, легко видеть, что условия (12) и (13) гарантируют выполнение условий (4) и (5) леммы 1, и все остальные условия теоремы 1 выполнены.

При d1 = d₂ = e₂ ж 0 следствие 1 совпадает с принципом максимума для уравнения смешанного гиперболо-параболического типа, приведенного в [8, с. 10]. Заметим, что условия (12), (13) следствия 1 при |a₂| = |b₂| ж const не имеют места, если с₂ = 0, так же, как и в [8, с. 17], поэтому этот случай должен быть рассмотрен отдельно.

ЗАМЕЧАНИЕ 1. Если в условии теоремы 1 функция и(х,у) удовлетворяет строгим неравенствам L1u > 0 в Q+, и L2 u < 0 в 11, то в формулах (5) и (9) неравенства будут нестрогие.