Принцип максимума в задачах оптимального управления процессами, описываемыми гибридными функционально-дифференциальными уравнениями

Рассматриваются задачи оптимального управления процессами, состояние которых описывается гибридными функциональнодифференциальными уравнениями [5,  13].

Если это обыкновенные дифференциальные уравнения, то эффективным средством исследования и решения таких задач является принцип максимума Понтрягина [14–16]. Если это функционально-дифференциальные уравнения, то можно их исследовать с помощью принципа максимума Понтрягина [2–4, 6–8, 14].

В качестве метода исследования и решения поставленных ниже экстремальных

Работа выполнена при финансовой поддержке РФФИ, № 18-01-00332 A.

задач здесь применяется классический принцип максимума, схема которого построена в статьях [9–12]. Это сделано из следующих соображений. Для систем управления, описываемых так называемыми уравнениями "нейтрального" типа, принцип максимума Понтрягина, вообще говоря, не применим [4, 6–8].

Класс обычно рассматриваемых экстремальных задач представляет собой задачи на условный экстремум с ограничениями типа равенств и неравенств, задаваемых системой функционалов, и явными ограничениями на управление. Результаты, приведенные в статьях [9–12], позволяют рассматривать экстремальные задачи с самыми разнообразными ограничениями.

Надо отметить, что в задачах, где применим принцип максимума Понтрягина, требуется меньшая степень гладкости по управ- лению, чем в рассматриваемых в работах [9– 12] экстремальных задачах.

1. Задачи линейной оптимизации. Постановка задач оптимального управления

Ниже рассматриваются задачи оптимального управления, в которых состояние управляемого процесса на отрезке времени t е [0, T ] описывается гибридными линейными функционально-дифференциальными уравнениями [1, 13].

Критерием оптимальности является минимум линейного ограниченного функционала общего вида l ₀: D n х nⁿ_{Q p} х L m х m™ ^ R , определенного равенством

T l0 (x, y, u, v) = j ^* (s)x(s)ds + ^*, x(0)^ + 0

tT

⁺ J ^ o ⁽ s ) u ⁽ s ) ^{ds +} ZX⁽ t ) y ⁽ t ) ⁺

T - 1

+ ^0*, y (-1)} + E%‘ (t) v (t).(1)

t = 0

Пусть Lnp, 1 < p < ^ , - пространство функций f: [0, T] ^ Rn, компоненты которых суммируемы на [0, T] со степенью p , и с нор- мой

/ т                Л¹/ p

II f\\  = JII f (t)||pndt . Dp, 1 < p ^ , - p      k 0              J пространство таких абсолютно непрерывных функций   x :[0, T] ^ Rn, что X е Ln, и

II x II D =1 x II L p + II x (0)||_R n .

Пусть пространство npnp , 1 < p < x , век- тор-функций g(t) = £ X[t,t+1)(t)g(t), которое t=0

изоморфно      пространству      матриц g = {g (0), g (1),..., g (T)} с нормой

/ T            A¹/ ^p

11 gl n =| Z II g JIr l .

p k i =0           J

Пространство nnOp,  1 < p < ^ , вектор- функций   y (t) = Z X[ t, t+1)(t)y (t), которое изо- t=-1

морфно       пространству       матриц y = {y(-1), y(0), y (I)»-, y(т)}     с нормой

/ T           k¹/ ^p

При записи функционала (1) используется естественный изоморфизм пространств D n и Lⁿ_p х M ⁿ , который задается формулой

t

x ( t ) = x (0) + J x ( s)ds . Аналогично использу- 0

ется изоморфизм пространств f_{0 p} и nⁿ _p х ® ⁿ , который задается формулой    y ( t )   =

Z Х [ t , t +1) ( t ) y ( t ) = y ( - 1) ^ - ₁ ,0 ₎ ( t ) + y (0) Х [0,1) ( t ) + + y (1) X [1,2) ( t ) + ... + y (T - 1) X [ T - 1 T ) ( t ) .

Основное ограничение на управляемый процесс задается системой гибридных линейных функционально-дифференциальных уравнений:

Z 1 x + Ly ^y —

= Q_u x + Д10 x (0) + Q ₁₂ y + A _n0 y ( - 1) —

— G_nu + G_nv + f ,

^21 ^{x +} 22 y ^{y —}

— Q 21 x + Л0 x (0) + Q 22 у + A 22O у ( - 1) — — G₂₁u + G₂₂v + g .

Операторы £ц : D p ^ Lⁿ _p , >^2: C p ^ L np , £21 : D n ^ f p , £22 : C p ^ nⁿ_p предполагаются линейными и ограниченными.

Предположим, что система (2) разрешима при всех f е L n и всех g е £_р .

Здесь £₁₁: D n ^ Lⁿ_p - линейный ограниченный оператор, Q _n : Lⁿ_p ^ Lⁿ_p - его главная часть, предполагается, что Q - нормально разрешим. Как правило, Q фредгольмов при естественных условиях его действия. A_n , A_n - матрицы со столбцами из Lⁿ_p ; A ₂₁, A₂₂ -матрицы со столбцами из nⁿ_p ; G _n : L m ^ Lⁿ_p -линейный замкнутый оператор, где m <  n ; f -элемент пространства    Lⁿ_p .    G ₁₂ : £ m ^ Lⁿ_p ,

G ₂₁: L m ^ Г_р , G ₂₂ : tmr ^ F _p - линейные замкнутые операторы, g - элемент пространства nⁿ_p .

Уравнение (2) охватывает широкий класс линейных гибридных уравнений с последействием. Типичными представителями этого класса являются: линейные обыкновенные дифференциальные уравнения, линейные уравнения с сосредоточенным и распределенным отклонением аргумента, линейные интегро-дифференциальные уравнения, линейные уравнения нейтрального типа, линейные разностные уравнения. Если оператор Q лишь нормально разрешим, то класс операторов (Z^J, вообще говоря, трудно обозрим. При этом, как правило, появляются дополнительные ограничения на гладкость оператора Gn. Фредгольмовость  Qn для большого класса экстремальных задач снимает практически все ограничения на оператор Gn .

Дополнительные ограничения:

T l (x, y, u, v) = j p* (s) x (s) ds + ^*, x (0)^ + 0

T

+ j ° ⁽ s ) u ⁽ s ) ds + ^ 0 * ⁽ t ) y ⁽ t ) + ($. , y ^(-0 +

T -1                                ____

+Тл(t)v(t)e Mi (i=1, k) • t=0

Ограничение (3) задается системой линейных ограниченных функционалов общего вида, определенных на D n х nⁿ_{Q p} х L m х m™ . Множества M. gR ( i = 1, к ) - выпуклы, могут быть точечными (ограничения типа равенств).

Преобразуем систему ограничений (3) следующим образом.

Определим линейный ограниченный вектор-функционал l: Dn х £пОр х Im х ^m > 1k равенством l (x, y, u, v) =

TT

= J Ф ( s ) x ( s ) ds + (T , x (0)} + j W ( s ) u ( s ) ds +

T-1

+ £©(t)y (t) + (S, y (-1)} + £Q( t )v (t), t=0

где Ф , T , W , © , S , Q -( к х n ) -матрицы, строки которых составлены из векторов р * , V i , o , , 0 i , & i , n i  ( i = 1, k ) •

Множество M _o e R ^k определим, полагая

^M 0 = { c°l{ y 1 ,..., y k ^}: y ^e M , (i = ^{1 k} ) } • Очевидно, что M - выпукло.

Итак, систему ограничений (3) можно записать в более удобном виде:

l ( x , y , u , v ) =

= | ф ( s ) x ( s ) ds + (T , x (0)} + J W ( s ) u ( s ) ds + 0                                         0

+ £ © ( t ) y ( t ) + (S , y ( - 1)} + t = 0

+ £ Q ( t ) v ( t ) e M 0 •         (3’)

t =0

Дополнительные фазовые ограничения на траекторию и управление:

A1 j x ⁺ ^2 j^{y + G} 11 j u ^{+ G} 12 j v =

= Q_n j x + A 11 j ( • ) x (0) + Q 12 j y + A 12 j ( • ) y ( - 1) ⁺

+ G 11 j u + G 12 j V e U j ,

4 1 j x ⁺ ^2 j y ^{+ G} 21 j u ^{+ G}22j^V =

= ^Q 21 j x ^{+ A} 21 j 0 x ^{(0) + Q} 22 j y ^{+ A}22 j ⁽ * ) y ^{( - 1) +}

+ G 21 j u + G 22 j V e V j  ( j = U) •

Ограничение (4) задается системой линейных операторов, определенных на элементах пространства D n х £^п_{О р} х L m х m^ и действующих в пространство L . Множества Uj , Vj G L 1 ( j = 1, k ) - выпуклы, могут быть точечными. По аналогии с ограничениями (3) ограничение (4) можно привести к более удобному виду:

£_ll x + 4 ₂y + G_nu + G₁₂v =

= Q_nx + A _n0 x (0) ■ Q2 y + A ^o y ( - 1) +

+ Gu + G₁₂v e U ,

_     _      _     _(4’)

Z^ x + £2 ₂ y + G₂₁u + G₂₂v =

= Q 21 x + A ^Q x ⁽⁰⁾ + ^Q 22 y + A 22 ⁽ - ⁾ y ^{( -} 1) ⁺

+ G₂₁u + G₂₂v e V ;

где      4 : Dn ^ Ip ,      4: Cp,

Д1: Dp >Zp , Д2: Г0 p  >. ;  Qu: In>

Q12: Cp >, Q21: Inp >, Q22: Cp >- их главная часть; Gn : Im > L , G12: £™ > L , G21: Im > 4 , G22: m > 4 ; An, A12 -(k х n) -матрица со столбцами из Ik1 , A21, A22 - (k х n) -матрица со столбцами из Zp ;

U g I , V g ^ k ¹ - выпуклые множества.

Отметим, что в ограничении (4) пространство правых частей L ^ и k¹^ выбрано таким образом исключительно для удобства работы. К операторам, действующим из Lⁿ_p , £П в L_p , £^к^ легко строить сопряжение.

Ограничение на управление:

u g U с L m , v g V с m™ .        (5)

Здесь U , V - выпуклые множества. Отметим, ограничение (5) является частным случаем ограничения (4).

В теории оптимального управления четверку ( x , y , u, v ) как решение уравнения (2) называют управляемым процессом, и называют допустимым управляемым процессом, если эта четверка удовлетворяет дополнительным ограничениям (3)-(5). Допустимый процесс ( x ₀, y ₀, u ₀, v ₀) называется оптимальным, если на нем достигается минимум функционала (1).

• 2.    Формализация задач линейной оптимизации

Экстремальной задаче (1)-(5) соответствует оператор F : L n х £}_р х R ⁿ х ⁿ х L m х £™ ^ Lⁿ_p х У^к х L q х L m , определенный равенством:

f 6 11	Q 12    A 11    A 12	- G 11   ■	- G 12 2	*
6 21	Q 22    A 21   A 22	- G 21   -	- G 22
Ф	©ST	W	-
б"	Q 12    A 11    A 12	G 11	G 12	=
6 21	Q 22    A 21   A 22	G 21	G 22
0	000	I	0
v 0	000	0	I ,
f 6 1	6 21    ф *	Q 11   Q 21	0	0 1
6 1 * 2	6 2*2     © *	Q 12   Q 22	0	0
:  4 1	J*       1—1* A 21    S	A 11    A 21	0	0
> 1	a 2*2   t*	A* 12      22	0	0
- 6	- G 2',   W ’	G 11    G 21	I	0
* V G 12	- G 22   - *	G 12   G 22	0	I J

, то уравнением, сопряженным к задаче (1)-(5), является

6 1 2 1 6 1 * 2 4 1	6 2 2 1 6 2 2 2 4 2 2 1	Ф 2 © 2 2 s	6 2 1 6 12 4 1	6 2 * 1 Q 22 A 21	0 0 0	0 1 0 0	f 2 2 2
4 2	4 2 2 2	t *	> 1 * 2	A 22	0	0	4
- G 1 * 1	- G 2 * 1	W *	G 1 2 1	G 21	I	0	-5 2
2 G 12	2 G 22	- 2	r2 G 12	G 22	0	1 J	6 V 2

f

h h3

h 4 ^h

I h 6 J

F { x , y , x (0), у ( - 1), u , v } =

fa,	Q 12	A 11	A 12	- G 11	G 12
6 21	Q 22	A 21	A 22	— G 21	- G 22
Ф	©	s	T	W	-2
6 11	Q 12	A 11	A 12	G 11	G 12	х
6 21	Q 22	A 21	A 22	G 21	G 22
0	0	0	0	I	0
1 0	0	0	0	0	I J

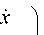
^y x (0) У ( - 1)

х

Для того чтобы сформулировать прин- цип максимума в поставленной задаче, оста- лось записать сопряженную краевую задачу. Для этого достаточно построить оператор, сопряженный к оператору F . Так как

• 3.    Принцип максимума

Здесь для задачи (1)-(5) формулируется принцип максимума.

Теорема. Пусть в сделанных предположениях пара (х0, у0, u0, v0) - оптимальный процесс в задаче (1)-(5). Тогда найдется функционал 2

{ Л 1 , 22Л ₄₉ 222 7 } g

L n_p ‘ х ^ П р' х ^^к х L^ х £ ^к^ х L mm х £^ , удовлетворяющий одному из условий:

• а)    Л - решение неоднородной системы уравнений (6) при { h , h , h , h ₄, h ₅, h ₆, h } = ^{{ h} 01 , ^h 02 , ^h 03 , ^h 04 , ^h 05 , ^h 06 , ^h 07 ^} ;

• б)    Л - нетривиальное решение однородной системы уравнений (6); для которого в точках li ( Х 0 , У 0 , u 0 , v ₀) ( i = 1, k ), Z^ x ₀ + Д2 y ₀ + G 11 u 0 ⁺ G 12 ^v 0 , £21 ^x 0 ⁺ 62 ^y 0 ⁺ G 2i ^u 0 ^{+ G} 22 v 0 , и u ₀, v ₀ выполняются следующие условия:

²i • l i⁽ x 0 , У 0 , u 0 , ^v 0 ) = min ² i • y ^},       ⁽⁷⁾

У ^е M i

^Л 4⁽ ^41 ^x 0 ⁺ ^2 y 0 ^{+ G} 11 ^u 0 ^{+ G} 12 ^v 0 ) =

= minЛ4(u1) ,(8)

u₁ e U

A ⁽ ^1 ^X0 + 22 y y 0 + G 21 u 0 + G 22 ^V 0 ) =

= minЛ5(Vi),(9)

v ₁e V

Аб(u0) = minАб(u) ,(10)

u e U

Л( V0) = min A( v).

u e V

Если функционал Л является решением неоднородной системы уравнений (6), то условия (7)–(11) являются достаточными условиями оптимальности.

Замечание. Условия принципа максимума (11) в таких задачах совпадает с принципом максимума Понтрягина. Условия (7)– (10) позволяют исследовать задачи с достаточно сложными фазовыми ограничениями.

В задаче (3)–(5) функциональнодифференциальные не обязательно должны быть уравнениями с запаздывающим аргументом. Решение сопряженной системы уравнений ищется в пространствах суммируемых функций. Поэтому снижаются требования на гладкость коэффициентов исходной задачи оптимального управления.