Принцип минимакса в теории и практике оптимального проектирования приводов современных зерноуборочных комбайнов
Автор: Радин Виктор Викторович, Лыков Евгений Васильевич
Журнал: Вестник Донского государственного технического университета @vestnik-donstu
Рубрика: Технические науки
Статья в выпуске: 1-2 (62) т.12, 2012 года.
Бесплатный доступ
Поставлена и решена задача оптимального выбора конструктивных параметров элементов приводов зерноуборочных комбайнов, когда эти элементы реализуются с помощью клиноремённых и гидравлических передач. Для этого использован принцип минимакса, реализованный с помощью метода оптимального проектирования параметров динамических систем в пространстве состояний под действием переменных нагрузок. Для формирования пространства состояний использована ранее полученная автором теоретическая модель динамической системы привода комбайна с нелинейными неголономными связями первого порядка.
Динамика привода зернокомбайна, нелинейная неголономная связь первого порядка, метод наискорейшего спуска, оптимальное проектирование
Короткий адрес: https://sciup.org/14249758
IDR: 14249758
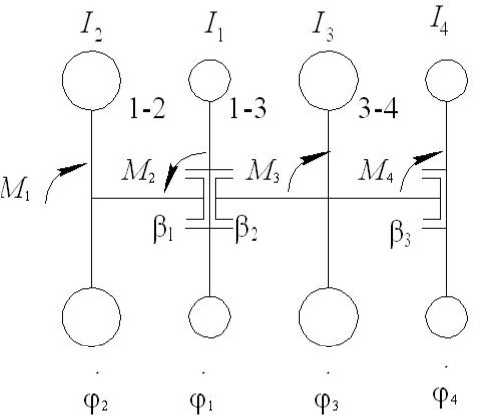
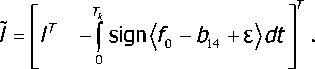
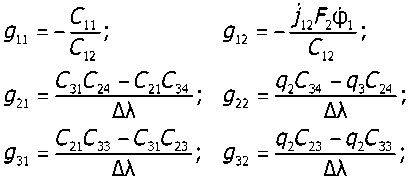
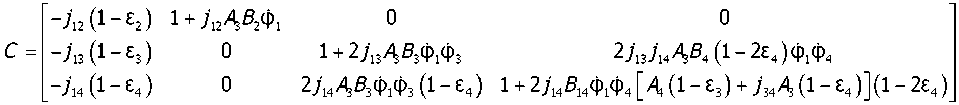
Список литературы Принцип минимакса в теории и практике оптимального проектирования приводов современных зерноуборочных комбайнов
- Радин, В. В. Динамика сложных неголономных систем на примере зерноуборочного комбайна/В. В. Радин, В. А. Бураков. -Ростов-на-Дону: РГАСХМ, 2003. -150 с.
- Хог, А. Прикладное оптимальное проектирование/А. Хог, Я. Арора. -Москва: Мир, 1983. -487 с.
