Принятие оптимальных педагогических решений с использованием линейного программирования

• –    множество допустимых объектов может оказаться пустым, тогда говорят, что система ограничений несовместна (то есть ограничениями выдвигаются противоречивые требования);

• –    множество допустимых объектов может оказаться не пустым, но среди его представителей не найдется удовлетворяющего критерию оптимальности.

Впрочем, существуют разрешимые задачи оптимальности, поэтому существует и предмет этой статьи.

Систематическое изучение педагогических задач оптимизации инициировано Ю.К. Бабанским. Под педагогической оптимизацией им понимается выбор педагогом наилучшего варианта реализации педагогического процесса, обеспечивающего при

выполнении всех выдвинутых условий наибольшей эффективности решения поставленных педагогических задач [2, с. 6].

Следует осознавать: оптимальное решение является наилучшим только в смысле удовлетворения конкретным ограничениям и соответствия вполне определенному критерию оптимальности. При изменении ограничений или критерия оптимальности решение, бывшее раньше наилучшим, может перестать быть таковым. Решение, оптимальное в одних условиях, может не быть оптимальным в других.

Математически универсум, из которого ограничениями выделяется множество допустимых объектов, можно представить как n -мерное линейное пространство ( n -натуральное число) над полем действительных чисел. Каждый элемент универсума есть вектор (x 1 ; ...; x_n) . Можно называть его и точкой. Ограничения могут определяться по-разному. В этой статье будем задавать ограничения системой неравенств:

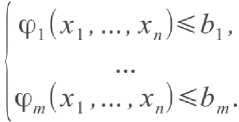
Здесь ф 1 , .„, ф_т - числовые функции n аргументов ( m - натуральное число, вовсе не обязательно равное n ); b 1 , „., b_m - некоторые действительные числа.

Критерий оптимальности тоже может задаваться различно. Мы будем формулировать его как требование достижения максимального или минимального значения некоторой числовой функцией n аргументов на множестве допустимых объектов. Эту функцию F(x 1 , .„, x_n) называют целевой функцией . Ясно, что в некоторой точке (x 1 , .„, x_n) функция F(x 1 , „., x_n) достигает максимального значения тогда и только тогда, когда в этой же точке функция Z(x 1 , „., x_n) = - F(x 1 , ..., x_n) принимает минимальное значение. Поэтому, не ограничивая общности, везде, где это необходимо, можно считать, что в формулировке критерия оптимальности выдвигается требование достижения целевой функцией именно максимального значения.

Учитывая сказанное, можно сформулировать математическую модель задачи оптимизации следующим образом: требуется найти n действительных чисел x 1 , „., x_n, удовлетворяющих заданной системе неравенств и дающих максимальное значение определенной целевой функции:

F^xv,..., х^-^тах

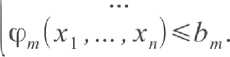
Эта математическая модель является задачей математического программирования.

Во многих предметных областях можно считать целевую функцию и функции, стоящие в левых частях системы ограничений, линейными формами своих аргументов. Кроме того, предметный смысл переменных x 1 , .„, x n часто требует часть ограничений свести к требованию неотрицательности значений переменных. Получаемый частный случай задачи математического программирования называется стандартной задачей линейного программирования на поиск максимума целевой функции :

F—c_x л^ + ... + с_пх_п->тах a_lvx_x+...+a_Xnx _n^b_v, а +... + « х ^b . ml 1          тп п т

X V А л-1 , . • • , л ^ / v

Все коэффициенты линейных форм Cj и aij (i=1..m, j=1..n) являются действительными числами.

В некоторых случаях удобнее явно требовать достижения целевой функцией не максимума, а минимума. Иногда ограничения уместно формулировать как неравенства со знаком «больше либо равно» или как равенства. Тогда (если сохраняется линейность всех функциональных форм) говорят о задаче линейного программирования , а отрасль математики, исследующая свойства таких задач и их решений, называется линейным программированием .

Впервые на важность исследования задач линейного программирования обратил внимание Л.В. Канторович [5], а первый универсальный (и широко применяемый в настоящее время) метод решения таких задач (симплекс-метод) предложен Дж.Б. Данцигом [4]. Им же выделены три типовые формы задач линейного программирования (стандартная задача линейного программирования на поиск максимума целевой функции, стандартная задача линейного программирования на поиск минимума целевой функции, задача линейного программирования в канонической форме) и предложен сам термин «линейное программирование». При исследовании ряда проблем линейного программирования применяется подход, впервые предложенный Ж.Б. Ж. Фурье и усовершенствованный Т. Моцкином - метод Фурье-Моцкина [4, с. 87]. Названные методы обладают, вообще говоря, экспоненциальной сложностью (количество

2 (7)/2018

ес/т/лм/^с

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

вычислений может чрезвычайно быстро возрастать при увеличении количества неизвестных и числа ограничений; метод Фурье-Моцкина обладает даже двойной экспоненциальной сложностью), поэтому в современной математике продолжается поиск новых подходов к решению задач рассматриваемого нами класса [1, с. 287; 8].

В педагогике пристальное внимание на возможность приложения линейного программирования обращено М.Г. Колядой [6, с. 139]. Им построена, в числе прочего, обобщенная формулировка педагогической задачи оптимизации, которую мы называем дальше стандартной задачей Коляды на максимизацию педагогического эффекта. Заметим, что М.Г. Коляда в известных нам работах не выполнял проводимую нами далее формализацию, а ограничился общими описаниями, примерами и классификациями другого рода. Тем не менее, из рассуждений М.Г. Коляды проводимая нами формализация следует с необходимостью.

Итак, организацию и реализацию любого педагогического процесса можно обобщенно представить как создание педагогом (коллективом педагогов, образовательной организацией) комплекса педагогических воздействий на обучающегося (воспитуемого, подопечного, группу, коллектив подобных субъектов): A 1 , …, A n . Для обозначения воздействий нами выбрана латинская буква A , потому что «действие» по-латыни будет «actio». Участие в педагогическом процессе требует от его участников наличия определенных личностных, материальных, моральных, физических и прочих ресурсов R 1 , …, R m . Общие запасы ресурсов, расходуемых при реализации педагогического процесса ограничены величинами Ь 1 , „., b m соответственно. Для реализации единицы воздействия A j (j=1..n ) необходимо расходование a ij единиц ресурса R i ( i=1..m ). Величины a ij образуют матрицу ресурсоемкостей педагогических воздействий, ее элементы будем называть ресурсоемкостями педагогических воздействий. Целью педагогического процесса является достижение некоторого суммарного педагогического эффекта F . Применение единицы воздействия A j (j=1..n ) приводит к появлению C j (j=1..n ) единиц целевого педагогического эффекта. Величины c j ( j=1..n ) будем называть эффективностями соответствующих педагогических воздействий A j (j=1..n ).

Предполагается обладание педагогическим процессом свойством аддитивности : например, если применение х 1 единиц воздействия A 1 порождает F 1 единиц целевого педагогического эффекта, а применение х₂ единиц воздействия A 2 порождает F 2 единиц этого эффекта, то применение x 1 единиц первого воздействия и x 2 единиц второго воздействия в комплексе приведет к появлению F 1 +F 2 единиц целевого педагогического

эффекта. Надо отметить, что реальные педагогические процессы обладают свойством аддитивности лишь приближенно (а иногда и приближенно не обладают): проявляется их синергизм [7, с. 129].

Наглядно система вышеописанных данных может быть представлена так, как это сделано в таблице 1.

Задача состоит в том, чтобы предложить план комплекса педагогических воздействий, то есть указать количества x 1 , …, x n включаемых в него единиц соответствующих воздействий A 1 , …, A n , таким образом, чтобы он не требовал расходования ресурсов в количествах, превышающих их запасы, и приводил бы к возникновению наибольшего из всех возможных суммарного педагогического эффекта. Это и есть стандартная задача Коляды на максимизацию педагогического эффекта.

Таблица 1. Компактное представление данных стандартной задачи Коляды на максимизацию педагогического эффекта

Ресурсы	Воздействия			Запасы ресурсов
	А,		А„
Ri	«и		ai„	bi
Rm	G-ml	...	VI mn	bm
Эффективности воздействий	Ci		Cn

Нетрудно видеть, что математической моделью стандартной задачи Коляды на максимизацию педагогического эффекта (при справедливости предположения о наличии свойства аддитивности) является стандартная задача линейного программирования на поиск максимума целевой функции (и именно она). Можно говорить и так: стандартная задача Коляды на максимизацию педагогического эффекта является педагогической интерпретацией (конечно же, не единственно возможной) стандартной задачи линейного программирования на поиск максимума целевой функции.

Далее мы предлагаем рассмотреть конкретный пример постановки и решения стандартной задачи Коляды на максимизацию педагогического эффекта. При этом отметим, что одной из серьезных проблем излагаемой теории является неопределенность (часто принципиальная) единиц измерения педагогических величин. Тем не менее, мы покажем, что эту трудность можно обойти путем апелляции к условным единицам

измерения и применения экспертного метода при оценке значений педагогических параметров.

Пусть изучаемым нами педагогическим процессом (и даже педагогическим явлением) является учебное занятие некоторого типа. Это может быть, например, урок для учащихся общеобразовательной школы или занятие профессионально-теоретической подготовки для студентов образовательного учреждения среднего профессионального образования. Нами рассматриваются 5 типов таких занятий: Т 1 – занятие формирования новых знаний обучающихся; Т 2 - занятие закрепления, углубления и расширения знаний обучающихся, формирования и развития их умений и навыков; Т 3 - занятие обобщения и систематизации знаний, умений и навыков обучающихся; Т 4 – занятие контроля знаний, умений и навыков обучающихся; Т 5 – комбинированное занятие (этот тип занятия может содержать элементы нескольких из вышеназванных «чистых» типов).

В качестве изучаемых нами педагогических воздействий выступают методы (а точнее - классы методов) обучения (за основу классификации взят характер учебнопознавательной деятельности обучающихся): A 1 - объяснительно-иллюстративные

(информационно-перцептивные) методы обучения , сущность которых состоит в том, что педагог разными способами сообщает готовую информацию, а обучающиеся ее воспринимают, осознают и фиксируют; A 2 - репродуктивные (воспроизводящие) методы обучения, сущность которых состоит в том, что педагог предлагает знания и способы деятельности в готовом виде, а обучающиеся усваивают их и воспроизводят, действуя точно по предложенному педагогом плану, алгоритму; A 3 - частично-поисковые

(эвристические) методы обучения, сущность которых заключается в том, что обучающиеся самостоятельно разрешают сложные учебные проблемы не от начала до конца, а лишь частично; педагог привлекает обучающихся к выполнению отдельных поисковых или нетривиальных шагов; часть знаний сообщает педагог, часть -обучающиеся добывают самостоятельно, отвечая на поставленные вопросы или разрешая учебные проблемы; A 4 - проблемные методы обучения, сущность которых заключается в том, что педагог или обучающиеся совершают постановку проблем и путем дидактического сотрудничества их решают, развивая тем самым комплекс учебнопознавательных, предметных и (возможно) профессиональных компетенций; A 5 - исследовательские (поисковые) методы обучения, сущность которых сводится к организации поисковой, творческой деятельности обучающихся по добыванию нового для них (субъективно нового) знания.

Будем считать, что до начала моделируемого процесса имеются в наличии и при его реализации используются (расходуются) следующие ресурсы: R 1 – внимание обучающихся; психический процесс, состоящий в том, что субъект направляет и сосредоточивает свое сознание на каком-то определенном объекте (процессе); R 2 – учебная активность обучающихся; в первую очередь она связана с наличием и качеством обратных связей между всеми участниками педагогического процесса; R 3 – эргопсихический ресурс (трудоспособность) обучающихся; запас их физических сил; R 4 – интерактивность обучающихся; их способность и готовность к учебному взаимодействию.

Здесь возникает проблема оценки ресурсоемкостей методов обучения каждого из классов по отношению к рассматриваемым ресурсам. Она может быть решена экспертным методом.

Каждого из восьми экспертов E 1 , …, E 8 (представителей профессорско-преподавательского состава кафедры инженерной и компьютационной педагогики факультета дополнительного и профессионального образования Донецкого национального университета; среди экспертов был и М.Г. Коляда) мы попросили выполнить ранжирование ресурсов в плане их значимости для эффективной реализации объяснительно-иллюстративных методов обучения (воздействия A 1 ): самый значимый ресурс оценивается числом 4, наименее значимый – числом 1. Полученные данные представлены в таблице 2.

аблица 2. Результаты ранжирования ресурсов R1, …, R4 по их значимости для воздействия A1 Ei      E2      E3      E4      Es     E6     E7     Eg Ri r2 Rs R4 4       3       4       4       4      4      4      4 2        4         2         2        3        1        3        1 1          2          3          1          1        2        2         2 3          1          1          3         2        3        1         3 Эти данные можно трактовать следующим образом: первый, например, эксперт оценил ресурсоемкость, например, a41 в 3 условных единицы, а второй эксперт оценил ту же величину в 1 условную единицу. Находя в каждой строке таблицы 2 среднее арифметическое и деля полученные средние по строкам на их сумму (с целью нормирования на единицу), получаем значения a11, …, a41 – первый столбец матрицы ресурсоемкостей рассматриваемых нами педагогических воздействий.

После повторения описанной процедуры (все эмпирические данные собраны и обработаны В.В. Воробъевой – одним из авторов этой статьи) для педагогических воздействий A 2 , …, A 5 получаем матрицу ресурсоемкостей в полном виде (таблица 3).

Таблица 3. Матрица ресурсоемкостей рассматриваемых педагогических воздействий

ati         Ai             А 2             А3	A 4             A 5
Rj        0,39           0,34          0,26 R2        0,22          0,18          0,26 R3        0,18          0,22          0,22 R4        0,21           0,26          0,26	0,25          0,20 0,28          0,30 0,30          0,26 0,17          0,24

Чтобы сформулировать для каждого из типов занятий T 1 , …, T 5 стандартную задачу Коляды на максимизацию педагогического эффекта, необходимо для каждого из них знать эффективности c 1 , …, c 5 педагогических воздействий A 1 , …, A 5 . Для оценки этих значений также можно применить экспертный метод.

Каждого из восьми вышеупомянутых экспертов мы попросили выполнить ранжирование педагогических воздействий A 1 , …, A 5 в плане их применимости на занятии типа T 1 : наболее применимое воздействие оценивается числом 5, наименее применимое – числом 1. Полученные данные представлены в таблице 4.

Эти данные можно трактовать следующим образом: первый, например, эксперт оценил эффективность c 4 в 4 условных единицы, а второй эксперт оценил ту же величину в 3 условные единицы. Находя в каждой строке таблицы 4 среднее арифметическое и деля полученные средние по строкам на их сумму (с целью нормирования на единицу), получаем значения эффективностей с 1 , …, с 5 педагогических воздействий A 1 , …, A 5 для занятия типа Т 1 .

Таблица 4. Результаты ранжирования педагогических воздействий A₁, …, A₅ по их применимости на занятии типа Т₁

	Ei	e2	E3	e4	E5	E6	e7	Es
Ai	5	4	4	3	5	5	5	5
A 2	3	5	5	5	2	4	3	4
A3	2	2	1	4	3	3	2	2
a4	4	3	3	2	4	2	4	3
A 5	1	1	2	1	1	1	1	1

После повторения описанной процедуры для типов занятий Т 2 , „., Т₅ получаем значения эффективностей педагогических воздействий для всех рассматриваемых типов занятий (таблица 5).

Таблица 5. Эффективности c j (j=1..5 ) педагогических воздействий A j для типов занятий T k ( k=1..5 )

с/к)	Т)            Т2            Т3             Т4             Т5
Ai А 2 Аз а4 А 5	0,30        0,20        0,17         0,15          0,24 0,26        0,26        0,16         0,24          0,16 0,16        0,25         0,28         0,20          0,24 0,21         0,17         0,19          0,15          0,25 0,07         0,12         0,20          0,26          0,11

Для каждого из типов занятий необходимо еще задать величины запасов Ь 1 , .„, Ь 4 ресурсов R 1 , .„, R 4 . При этом нет необходимости прибегать к измерительно-оценочным процедурам. Действительно, поскольку все оцененные параметры измерены в условных единицах (и смысл имеют не абсолютные значения, а лишь отношения между ними), то появляется свобода в выборе единиц измерения для величины каждого из запасов. Значит, всегда можно выбрать эти единицы измерения таким образом, чтобы величины запасов ресурсов для всех типов занятий были равны 1 (или 100 %).

Теперь может быть поставлена для каждого из типов занятий стандартная задача Коляды на максимизацию педагогического эффекта. Все эти пять задач педагогического содержания сведены нами к соответствующим им задачам стандартным задачам линейного программирования на поиск максимума целевой функции (математическим задачам), каждая из которых решена симплексным методом. Для автоматизации процесса решения использовано средство РЕШАТЕЛЬ (SOLVER) процессора электронных таблиц Open Office CALC [9]. Компоненты каждого вектора-решения затем нормированы на единицу - тем самым определены оптимальные доли каждого из изучаемых педагогических воздействий в структуре занятия каждого из типов (и подчеркнут относительный, а не абсолютный смысл полученных числовых значений). Доли оптимальны в смысле достижения занятием каждого из типов наибольшего суммарного педагогического эффекта. Названные результаты представлены в таблице 6.

Таблица 6. Оптимальные доли педагогических воздействий A₁, …, A₅ в структуре занятий каждого из типов T₁, …, T₅

	Ti	T2	T3	T4	Ts
A,	0,19	0	0	0	0
a2	0	0	0	0,38	0
Аз	0	1,00	1,00	0	1,00
a4	0,81	0	0	0	0
A5	0	0	0	0,62	0

Обращает на себя внимание тот факт, что содержательная (педагогическая) интерпретация полученных нами результатов является далеко не тривиальной.

Характеристики типов Т 2 , Т 3 и Т 5 совершенно идентичны. Это означает, что в контексте оптимального использования педагогических ресурсов с целью получения максимального педагогического эффекта традиционная типология занятий (изначально принимаемая нами) является избыточной: ее можно упростить, оставляя только три различных типа занятий (их можно с целью недопущения терминологического конфликта назвать «сверхтипами»):

СТ 1 – перцептивный сверхтип; представлен одним типом Т 1 ; основной целью таких занятий должно быть эффективное восприятие нового учебного материала; проблемное изложение для этих занятий оказывается даже более востребованным (около четырех пятых), чем традиционное объяснительно-иллюстративное преподавание (около одной пятой);

СТ 2 – эвристический сверхтип; представлен типами Т 2 , Т 3 , Т 5 ; основной целью таких занятий должно быть всестороннее развитие знаний, умений, навыков и (быть может) профессиональных компетенций обучающихся в ходе осуществления ими под управлением педагога частично-поисковой учебной деятельности;

СТ 3 – контрольный сверхтип; представлен типом Т 4 ; основной целью таких занятий должен быть контроль учебных достижений обучающихся, реализуемый путем выполнения ими заданий как репродуктивного (около одной трети), так и исследовательского (около двух третей) характера.

Общие выводы, к которым мы приходим на данном этапе, следующие.

• 1.    Общепедагогическая методология оптимизации является в настоящее время

• 2.    Математическая теория оптимизации в настоящее время развита вполне достаточно для того, чтобы обеспечивать исследователей и практиков (в частности педагогов) математическими методами и вычислительными инструментами. В связи с этим следует приветствовать и продолжать математико-педагогические исследования, в том числе – и исследования в области вычислительной (компьютационной) педагогики.

• 3.    Что же касается собственно компьютационной педагогики (особенно такого ее раздела, как принятие педагогических решений и прогнозирование педагогических результатов на основании критериев оптимальности), то следует отметить (наряду с несомненными достоинствами этой теории) слабую проработанность отдельных деталей точного соответствия между используемыми математическими моделями и их педагогическими интерпретациями . В этой статье нами устранен лишь один из подобных пробелов: построена четкая педагогическая интерпретация стандартной задачи линейного программирования на поиск максимума целевой функции в форме педагогической задачи, которую мы предложили называть стандартной задачей Коляды на максимизацию педагогического эффекта. Мы полагаем, что такие педагогико-математические сопоставления плодотворны и в теоретическом, и в методологическом (пример – полученные нами сверхтипы учебных занятий), и в практическом аспекте.

разработанной на вполне достаточном для потребностей педагогической науки и практики уровне. Основная заслуга в этом принадлежит Ю.К. Бабанскому (и другим представителям его научной школы). Сказанное не означает, что дальнейшее развитие в данном вопросе невозможно. Мы лишь хотим подчеркнуть тот факт, что возможности чисто качественных (в противовес количественным) способов и построений в данной отрасли близки, по нашему мнению, к исчерпанию.