Принятие управленческих решений путем определения класса коммерческой недвижимости методом сходства и включения

Рассмотрим порядок отнесения того или иного объекта коммерческой недвижимости к классу А, В+ или В. Первоначально приведем классификацию параметров:

Категории отнесения	Класс А	Класс В+	Класс В
Местоположение/доступность	1	1	1
Срок службы	1	1	1
Репутация/положение на рынке	1	1	0
Состояние здания: внешние элементы	1	1	1
территория	1	0	0
общие площади	1	0	1
офисные площади	1	1	1
прочие	1	0	0
Системы здания: лифты	1	1	1
вентиляция	1	1	1
ночная охрана	1	1	0
безопасность	1	1	1
прочее	1	0	0
Наличные площади: местоположение	1	1	0
половое покрытие	1	1	1
оконные модули	1	1	1
прочее	1	0	0
Парковка: откр./закр./ гараж	1	1	1
гостевые места	1	0	0
стоимость для арендатора	1	0	0
прочее	1	0	0
Комфортабельность/особенности	1	1	0

Представленная матрица характеризует только качественные показатели отнесения бизнес-центра к тому или иному классу, поскольку количественными показателями может быть выражена только цена аренды, к тому же ее можно заменить словами «высокая» или «низкая». Международная классификация офисных помещений основана именно на качественных показателях. Используем для определения класса объекта метод включения . Он отражает меру включения одного объекта в другой и позволяет выявить, какой из двух сравниваемых объектов содержит больше специфических признаков, т.е. какой из них более оригинален, а какой более типичен для множества анализируемых объектов. Мера включения множества S₂ во множество S₁ и S₁ в S₂ определяется следующим образом: W(S₁; S₂)=

m (S 1 ^П S 2 )             ,     m ⁽S i ⁿ S 2 )

=     1    2 , W(S1; S2) =               . (1.1)

m (S₁ )                       m (S₂)

Меры включения несимметричны, а включение J-го описания в самом себе стопроцентно, т.к. m(Sj ∩ Sj) = m(Sj). Для более полного анализа множеств исследуемых объектов рас- считываются меры сходства и включения для всех пар объектов. Полученные после вычислений значения соответствующих мер сводятся в квадратные матрицы порядка q х q, номерами строк и столбцов которых являются номера изучаемых объектов.

Алгоритм построения матриц отношения сходства и включения

Этот алгоритм отличается для указанных двух мер лишь методом расчета значений матриц сходства и включения.

Шаг 1. Формируются два множества: множество исследуемых объектов J = { S_1, S₂,…, S_q} и множество признаков Z = { Z₁ Z₂,… ^, , Z_p}. Каждый объект S_i является подмножеством признаков Z _ е Z , выступающим качественным признаковым образом. Все образы объектов систематизируются в матрицу образов, где представляются индексированными множествами. В нашем примере множеством исследуемых объектов будут являться объекты коммерческой недвижимости соответствующего класса, а множеству признаков будут соответствовать категории отнесения (см. табл.).

Шаг 2. Генерируются все парные сочетания объектов, для каждой пары описаний объектов Si и Sj строится матрица В = = xij ; i = 1,p; j = 1, 2, где р – число строк матри- цы образов, соответствующее числу рассматриваемых признаков m (Z). На основе матрицы рассчитываются меры сходства С(Si; Sj) или включения W(Si; Sj). Для определения меры сходства может быть использована одна из формул, указанных выше. Расчет мер включения осуществляется по формулам (1.1) [1, c. 127]. Тогда применительно к нашему примеру, получаются следующие показатели:

Матрица В

	S1	S2	S3
Z1	1	1	1
Z2	1	1	1
Z3	1	1	0
Z4	1	1	1
Z5	1	0	0
Z6	1	0	1
Z7	1	1	1
Z8	1	0	0
Z9	1	1	1
Z10	1	1	1
Z11	1	1	0
Z12	1	1	1
Z13	1	0	0
Z14	1	1	0
Z15	1	1	1
Z16	1	1	1
Z17	1	0	0
Z18	1	1	1
Z19	1	0	0
Z20	1	0	0
Z21	1	0	0
Z22	1	1	0

2 ² xi 1 xi 2

Мера сходства с ( s 1 , s 2 ) = 22  ¹ 22 —= 22—14 = 0,78.

2 x, i ⁺ 2 x2

i = 1 i = 1

² xi 1 xi 2    14

Мера включения W ( s 1 , s ₂ ) = i = 22 ---= ~ = 1.

2 X 2    ¹⁴

i = 1

² xi 1 xi 2

Мера включения w ( s ₂ , s 1 ) = i = 22---= — = 0,63.

2 x, i    ²²

i = 1

^{2 2} x 1 ^Xi 3

Мера сходства с ( s 1 , s ₃) = ₂₂ ‘=1 ₂₂—

2 x,i + 2 х,з i=1

2 - 11

22 + 11

= 0,67.

² xi 1 ^x ,3 ii

Мера включения W ( s 1 , s ₃ ) = ^= 22---= — = 1.

2 х,з i=1

2 xn Xi3

Мера включения W ( s ₃ , s 1 ) = ^= 22---= — = 0’5.

2 x,1

i = 1

2 2 Xi2Xi3

Мера сходства с ( s 2 , s 3 ) = ₂₂ ⁱ = 1 ₂₂ — = ^—^ = 0,8.

2 x ,2 + 2 x , 3   ^{14 + 11}

i=1

2 xi 2 xi 3

Мера включения w ( s 2 , s 3 ) = ⁱ = 22----= — = 0,9.

2 x,3

i = 1

2 x13xi2

Мера включения W ( s ₃ , s ₂ ) = ⁱ = 22----= — = 0,714.

2 Xi2

i = 1

Шаг 3. На основе рассчитанных на шаге 2 значений мер сходства и включения (матрица В) строятся соответствующие матрицы размерностью qxq - матрица мер сходства (С) и матрица мер включения (D).

	Матрица С
	S1	S2	S3
S1	1	0,78	0,67
S2	0,78	1	0,8
S3	0,67		1
Матрица мер сходства Матрица D
	S1	S2	S3
S1	1	0,63	0,5
S2	1	1	0,714
S3	1	0,9	1

Матрица мер включения

Матрица мер сходства симметрична относительно главной диагонали, а матрица мер включения таким свойством в общем случае не обладает. В приведенной матрице включения число 0,63 (второй столбец и первая строка) – W(S2;S1), а число 1 (первый столбец и вторая строка) соответствует W(S1;S2). Таким образом, индекс при названии первого множества в скобках указывает номер столбца, а второе – номер строки матрицы включения. При построении матрицы сходства индекс при первом множестве в мере сходства указывает на номер строки матрицы, а при втором – номер столбца.

Шаг 4. Задается отношение сходства или включения в следующем виде: <  C A , J >= { s , , s j е J |с ( s , , s j ) >  а } ;

< W A , J >= { s , , s j е J W ( s , , s, ) > A } ;

где A - произвольное число, (0 <  A <1); i , j е J .

Для заданного значения «дельта» строится матрица сходства (матрица Е) или включения (матрица F), в которой все значения, большие или равные «дельта», заменяются единицами, а оставшиеся – нулями.

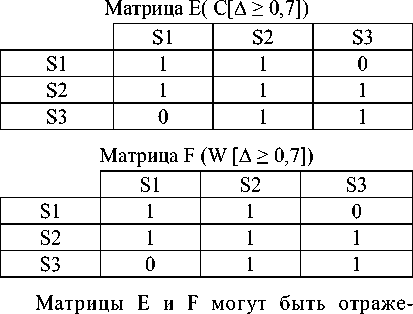
ны графами и орграфами соответственно (рис. 1–2). Дуги и стрелки соединяют те объекты, которые имеют единицу на пересечении соответствующих строк и столбцов матриц. Направление стрелки в графе отношения включения устанавливается таким образом, что она начинается в вершине графа, соответствующего Si-объекту, принадлежащему i-й строке матрицы, и заканчивается в Sj-м объекте, принадлежащем j-му столбцу матрицы. При этом Si-й и Sj-й объекты должны быть связаны отношением включения, т.е. иметь на пересечении Si-ого и Sj-ого объектов в матрице отношений включения единицу. Чем больше стрелок входит в тот или иной объект, тем более он оригинален по сравнению с другим объектом. Например, наиболее оригинальным являются объекты S2 и S3. При практическом использовании вышеприведенных отношений величину «дельта» находят путем перебора серии значений, добиваясь при этом установления всех существенных связей.

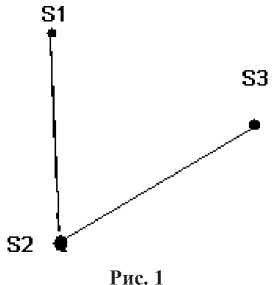
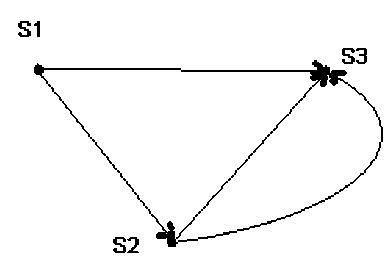
Рис. 2

Обработка количественных признаков образов

Для случая применения количественных данных:           m

m (Sj Q Sk) = Z min(Xy, x,k );

i = 1

m

m(Sj Q Sk) = Z max(Xj, х,^), i =1

где n – число признаков, представляющее объединение множеств признаков двух текущих сравниваемых описаний объектов Sj и Sk.

Пусть даны три объекта S1, S2, S3, которые охарактеризованы опытным путем по множеству критериев качества: K1 – ме-стоположение/доступность, К2 – репута-ция/положение на рынке, К3 – срок службы, К4 – состояние здания (внешние элементы), К5 – территория, К6 – общие площади, К7 – офисные площади, К8 – прочие, К9 – системы здания (лифты), К10 – вентиляция, К11 – ночная охрана, К12 – безопасность, К13 – прочее, К14 – наличные площади (местоположение), К15 – половое покрытие, К16 – оконные модули, К17 – прочее, К18 – парковка (откр./закр./ гараж), К19 – гостевые места, К20 – стоимость для арендатора, К21 – прочее, К22 – комфортабель-ность/особенности.

Описание объектов имеет следующие качественные значения:

	K1	K2	K3	K4	K5	K6	K7	K8	K9	K10	K11...
S1	5	5	5	5	5	5	5	5	5	5	5
S2	4	5	3	4	3	3	2	1	3	3	3
S3	3	5	2	3	2	2	1	1	2	2	2

	...K12	K13	K14	K15	K16	K17	K18	K19	K20	K21	K22
S1	5	5	5	5	5	5	5	5	5	5	5
S2	2	1	3	4	5	2	5	2	4	2	4
S3	1	3	3	2	3	1	4	1	3	1	3

Найдем меры сходства и включения описаний S1, S2, S3.

Мера сходства

QSS1. 2 m (S,n S2)? ,Xmm( -"X'2'_

C ( S i , S') I                                                                   0, /64.

*’ 2 m(S,) + (S2)    22    ^ 22       110 + 68’ v 12 v 22    X Xi1 + X xi2

i=1

Мера включения

X min ^x _n ^x - 2 )

W ( S 1 , S 2 ) =       ..--------

X X -2

i = 1

Матрица Н

	S1	S2	S3
S1	1	0,618	0,454
S2	1	1	0,735
S3	1	1	1

Мера включения

W ( S 2 , S _t) =

X min( x_nX i2 ) i = 1

X X i 1 i = 1

68 = 1.

-68 = 0,618.

110     ^,

Мера сходства

^{2 m ( S} 1 H ^S 3 )

C (S1,S 3 ) =               = m (S1) + (S3)

2 X min( x_fl x_i3 ) i =1 ___________________

22      22

X x - 1 + X x - 3

i = 1         i = 1

00 = 0,625.

Мера включения

X mi ⁿ⁽ x_nx i 3 )

W ( S„ S 3 ) =     2.------

X x - 3

i = 1

.

Матрица мер сходства

Задается отношение сходства или включения в следующем виде:

• <    C A , J >= { S i , S j e J C ( S i , S j ) >a } ;

• <    W A , J >= { S i , S j e J W ( S i , S j ) > A } ,

где A - произвольное число (0 <  A <1); i , j e e J .

Для заданного значения «дельта» строится матрица сходства (матрица Е) или включения (матрица F), в которой все значения, большие или равные «дельта», заменяются единицами, а оставшиеся – нулями.

Мера включения

W ( S 3 , S 1 ) =

X min( X i 1 X i 3 )

i = 1

X ^xi 1 i = 1

⁰⁰ = 0,454.

Мера сходства

C ( S 2 , S 3 ) =

2 m ( S 2П S ₃ ) = ^{2 X ml} n x i 2 x - 3 )

m ( S 2 ) + ( S 3 )     22       ²²

^X x i - 2 ^{+ X} x i 3 i = 1          i = 1

¹⁰⁰ = 0,847.

X min ^x i2 ^x i3 )

Мера включения W ( S ₂ , S ₃ ) = i = ¹₂₂------

X x - 3

i = 1

50 = 1.

	Матрица К (C[ A > 0,7])
	S1	S2	S3
S1	1	1	0
S2	1	1	1
S3	0	1	1
Матрица L (W [ A > 0,8])
	S1	S2	S3
S1	1	0	0
S2	1	1	0
S3	1	1	1

X mm ^{( х} - з ^xi 2 )

Мера включения w ( s ₃ , s 2 ) = i =L__-----

X ^xi 2

i = 1

⁵⁰ = 0,735.

68     ^,

Из приведенных значений видно, что при определении числа на пересечении двух множеств подсчитывается сумма минимальных значений, образующих эти множества, а при определении числа элементов множества суммируются все его значения. Далее строится матрица мер сходства и включения для числовых количественных значений признака.

Матрица G

	S1	S2	S3
S1	1	0,764	0,625
S2	0,764	1	0,847
S3	0,625	0,847	1

Матрица мер включения

Матрицы К и L могут быть отражены графами и орграфами соответственно (см. рис. 3– 4). Дуги и стрелки соединяют те объекты, которые имеют единицу на пересечении соответствующих строк и столбцов матриц. Направление стрелки в графе отношения включения устанавливается таким образом, что она начинается в вершине графа, соответствующего Si-объекту, принадлежащему i-й строке матрицы, и заканчивается в Sj-м объекте, принадлежащем j-му столбцу матрицы. При этом Si-й и Sj-й объекты должны быть связаны отношением включения, т.е. иметь на пересечении в матрице отношений включения единицу. Чем больше стрелок входит в тот или иной объект, тем более он оригинален по сравнению с другим объектом. Например, наиболее оригинальным является объект S2.

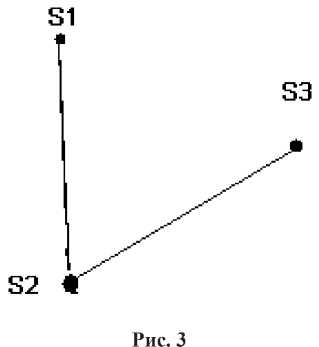
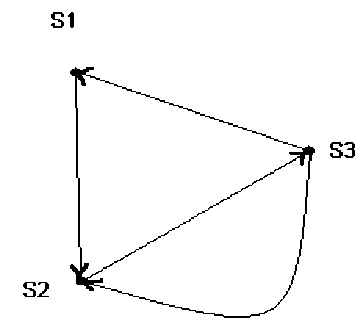
Рис. 4