Приведение возмущенного движения точки на базовую траекторию при наличии геометрических ограничений на дополнительные управления
Автор: Лутманов С.В.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика
Статья в выпуске: 3 (62), 2023 года.
Бесплатный доступ
В статье решена задача вывода возмущенного движения материальной точки в малую окрестность базовой траектории в предположении, что на дополнительные управления наложены геометрические ограничения в форме выпуклых компактных множеств. В частности, были рассмотрены случаи шаров, эллипсоидов и прямоугольных параллелепипедов. В результате построенного управления были удовлетворены все требования, предъявляемые к кинематике полета точки: запрет попадания точки в заданные области и необходимость ее нахождения в заданной вертикальной полосе над поверхностью земли. Проведенный численный эксперимент подтвердил эффективность предложенного алгоритма.
Кинематический закон движения, базовая траектория, фазовые ограничения, программное управление, малая окрестность
Короткий адрес: https://sciup.org/147246630
IDR: 147246630 | УДК: 517.977.5 | DOI: 10.17072/1993-0550-2023-3-44-54
Текст научной статьи Приведение возмущенного движения точки на базовую траекторию при наличии геометрических ограничений на дополнительные управления
лицензии, посетите
В работе решается задача совмещения, возмущенного и базового движений управляемой точки в заданный момент времени полета. Базовое движение построено автором в статье [1]. Это совмещение осуществляется дополнительным управлением, которое обнуляет возмущения – разность между возмущенным и базовым движениями. Динамика возмущений адекватно описывается линейным векторным дифференциальным уравнением, являющимся линеаризацией в окрестности пары "базовое управление, базовое движение" исходного дифференциального уравнения управляемого движения точки. В дальнейшем дополнительное управление отключается, и точка продолжает свое движение в соответствии с базовым законом движения, что обеспечивает выполнение всех требований, предъявляемых к ее кинематике. Задача решается в предположении, что на дополнительное управление наложены геометрические ограничения. Обычно они возникают, когда выбор оптимального управления, минимизирующего функционал качества, ограничен требованиями, отражающими технические характеристики устройств и условий эксплуатации. Заметим, что наличие ограничений на состояния и управляющие воздействия в виде уравнений или неравенств существенно осложняет решение задачи оптимального управления.
Некоторые подходы построения решения задачи оптимального управления для этого случая представлены в [2–10].
Тот факт, что динамика возмущений описывается линейными дифференциальными уравнениями, позволяет привлечь к решению задачи обнуления возмущений линейную теорию оптимального управления [11–19]. Например, задачи управления с выпуклыми функционалами качества допускают, как известно [15], естественную двойственность с задачами математического программирования. Данное свойство является следствием общего принципа двойственности, установленного Н.Н. Красовским и сформулированного им в терминах проблемы моментов [15].
Использование этого принципа позволило построить эффективные методы решения линейных задач управления на основе сведения задач минимизации в функциональном (бесконечномерном) пространстве к более простым задачам максимизации в конечномерном векторном пространстве, доставляющим оптимум исходным задачам. Этот подход к решению линейных задач управления, который был досконально изучен в работах Н.Н. Красовского, А.Б. Куржанского, Ю.С. Осипова, А.И. Субботина и их учеников, применен автором в представляемой статье.
1. Дифференциальные уравнения движения
Динамика полета описывается обыкно-
венным нением
векторным дифференциальным урав-
r
r
+ g , t g [ 1 0 , T ] ,
где t - текущее время,
r = y g R 3 — радиус-вектор точки относи-
z
тельно начала координат,
m — масса точки,
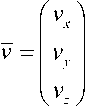
g R 3 — вектор основных управляю-
щих параметров,
g R 3 — вектор
дополнительных
управляющих параметров,
компонентами векторов v, u являются проекции вектора управляющей силы на соответствующие оси, g — вектор ускорения силы тяжести, k — коэффициент пропорциональности.
В координатной форме векторное уравнение (1) имеет вид k222
X —-- уХ + y + Z X + m
+ — ( V x + U x ) , m
|
k y —--V x 2 + У + z m + - ( v y + u y ) , m |
y + |
t e [ 1 0 , T ] |
|
1---------------------------------------------- k z —-- V x 2 + y + z m + - ( vz + uz ) — g . m |
z + |
Запишем эту систему в нормализованной форме pl — P 4,
P 2 — P5, p3 — P 6, k 222
p 4 —--- V p 4 + p 5 + p 6 ’ p 4 +
m
+_ ( v l + u l ) ,
m k 222
p 5 —--- V p 4 + p 5 + p 6 ’ p 5 +
m
+ — ( V 2 + U 2 ) ,
m k 222
p 6 —--- V p 4 + p 5 + p 6 • p 6 - g +
m
+ _( v3 + u 3),
m где pi — x, p 2 — y, p3 — z, p4 — X, p^ — y, p 6 — z, vl — vx , V2 — vy , V3 — vz ,
.
U — ux , u2 — uy , u3 — uz .
Обозначим через pbaz ( t ) —
' 1 (t Г pbaz 2 ( t ) pbaz 3 ( t ) pbaz 4 ( t ) pbaz 5 ( t ) у pt>az6 (t )j vbaz ( t ) —
' V baz 1 ( t Г v baz 2 ( t )
p
voz
1
(
t
)
p
voz
2
(
t
)
p
voz
3
(
t
)
p
voz
4
(
t
)
p
voz
5
(
t
)
p
voz
6
(
t
)
t
^
[
1
0
,
T
]
соответственно базовый закон движения, возмущенный закон движения, отвечающий начальным условиям pvoz 1 ( t0 ) pvoz 2 ( t0 ) pvoz 3 ( t0 ) pvoz 4 ( t0 ) pvoz 5 ( t0 ) у pvoz 6 ( t0 )J
^
p
10 '
(x
A
x
0
p
20
y
0
p
30
z
0
p
40
x
0
p
50
y
,
У
p
60
J
у
z
0
J
и базовое программное управление в новых переменных. Выведем дифференциальные уравнения управляемого движения, описывающие динамику возмущений:
'
5
p
voz
1
(
t
Г
S
p
voz
2
(
t
)
5
pvoz
3
(
t
)
5
p
voz
4
(
t
)
5
p
voz
5
(
t
)
у
5
p
voz
6
(
t
L
—
5
p
(
t
)
—
p
voz
(
t
)
-
p
baz
(
t
)
.
С этой целью линеаризуем систему (1) в окрестности пары "базовое программное управление, базовое движение" на промежутке времени t e[ t0, T ], где T < t — планируемый момент стыковки возмущенного и базового движения точки. В результате получим систему линейных дифференциальных уравнений:
x
=
A
(
t
)
x
+
Bu
,
t
e
[
t^
,
T
]
,
x
=
x1 x x3 x4
x
5
x
,
u
=
u
1
u
2
u
A
(
t
)
*
6
x
6,
B
^
6
x
3
относительно шести мерного фазового вектора
x
e
R
6
, для которого
=
p
voz
(
t
)
-
pb
az
(
t
)
.
t
e
[
t
0
.
T
1
]
’
Здесь A (t )=
"
O
<
O
E "
p
=
P
baz
, П =
,
O
=
0
0
,
0
2. Корректировка возмущенного движения В предположении, что на вектор управляющих параметров наложено геометрическое ограничение в форме
u
1
u
2
u
e
P
,
^A P • p 4 )••• dp 4 ^(P • p^ )- dp 4
P
•
p6)
бp4(
^(
P
■
p
4
)
d
p
6
^( P ^ p5 )
d
p
6
d
p
6
,
где
P
о
R
3
—
выпуклый компакт, поставим задачу о приведении фазового вектора
x
e
R
6
линейного динамического объекта (2) из положения
5
p
(
t^
)
в момент времени
1
0
в начало координат в момент времени
T
1
.
Задачу приведения будем решать в классе интегрируемых программных управлений
и
(
•
)
, для которых
u
(
t
)
e
P, t
e
[
tQ
,
T
]
. Множество таких программных управлений обозначим символом
П
[
t
0,
T
]
.
Пусть
u
(
-
)
еП
[
t
0,
T
]
. Символом
x
(
t
,
1
0
,
x
0
,
u
(
•
)
)
,
t
e
[
t^
,
T
]
обозначим решение
x
(
t
)
,
t
e
[
t
0,
T
]
дифференциального уравнения (2), для которого
x
(
t
0 )
=
x
0 .
Определение 1.
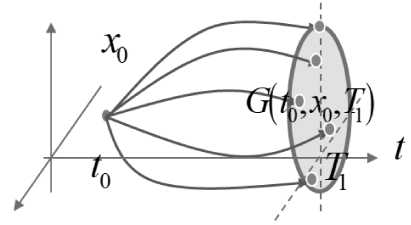
Множество
G
(
t
»
.
x
,„
T
i
)
=
=
{
q
=
x
(
T
.
1
0
,x
„
,u
(
■
))!
u
(
-
)
еП
[
t
0
,T
]
}
c
R6
называется областью достижимости управляемого динамического объекта в момент времени
T
1
для начального положения
{
t
0,
x
0 }
.
P
= —
k
222
Л/
p
4
+
p
5
+
p
6
,
m
B
= —
m
0
^
.
Рис. 1.
Область достижимости
Известно [16], что множество достижимости является выпуклым компактом.
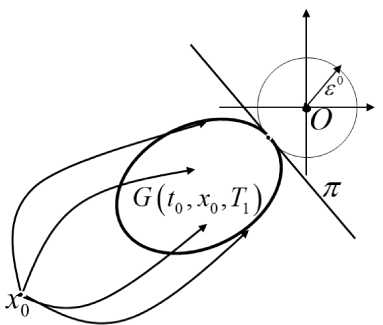
Определение 2
.
Величину
€
0 (
t
0,
x
0)
=
min
{
^ >
0|
G
(
t
0,
x0
)П
м
s
*0
}
,
(см. рис. 2)
где символом
M
€
обозначена замкнутая
€
—
окрестность начала координат, будем называть гипотетическим рассогласованием в позиции
{
t
0,
x
o }
.
Доказательство.
От противного приходим к существованию векторов
l
^)
,
l
(
2
) е
S
(
0,1
)
,
l
(
1
) *
l
(
2
)
, для которых
€ = min qq, l^1) \, qеG(10,x0,T1) V / € = min (q, l(2)k q^ G (t 0,x 0, T1 P '
Рис. 2.
Гипотетическое рассогласование
Сложим эти равенства почленно:
2
€
min
q
е
G
(
t
0
,
x
0
,
T
1
)
В силу компактности множества
G
(
t
0,
x
0,
T
)
минимум в правой части послед-
него равенства существует. Геометрический смысл гипотетического рассогласования состоит в том, что оно совпадает с наименьшим расстоянием, на которое может приблизиться фазовый вектор линейной динамической системы (2) к началу координат в момент вре- мени
T
1
.
Заметим, что если
0
е
G
(
t
0,
x
0,
T
)
, то
€
(
t
0
,
x
o
)
=
0.
Из [20] следует, что
€
(
t
o
,
X
o
)
=
{
max
{
0,
}
,
min
q
е
G
(
1
0
,
x
0
,
T
1
)
< min
qq
,
l
^ +
1
(2Л . (4)
qеG
(
1
0
,
x
0
,
T
1 )\ /
Из неравенства (4) следует, что
l
()
* —
l
( )
, а
из условия
l^ * l
^ )
следует, что
<
2
. Полагаем:
l
(
1
)
+
1
(
2
)
е
S
(
0,1
)
.
Тогда из (3) выводим: = €° .
(q, l)
}
,
max min lеS(0,1) LqeG(10,x0,T1) S(0,1) = {l е R6| |||| = 1}.
Следующие два утверждения являются обоснованием алгоритма построения программного управления
u
(
e
)
(
•
)
е П
[
t
0,
T
]
, реализующего стыковку возмущенного и базового движений.
Теорема 1
.
Пусть
€
(
t
0,
x
0 )
>
0
. Тогда максимум в (3) достигается на единственном векторе
l
0 е
S
(
0,1
)
.
Получили противоречие, которое и доказывает единственность максимизирующего вектора
l
0 е
S
(
0,1
)
. Теорема доказана.
В силу формулы Коши [15], которая в рассматриваемом случая имеет вид q = X [T, 10 ] x +
T
1
JX[Tt]B(т)u(r)dT, t0 где X [t,t] , t, т е [t0, T ] - фундаментальная матрица Коши для однородного уравнения x = A (t) x, формуле для гипотетического рассогласования можно придать вид
£
(
t
0
,
X
»
H
X
[
T'
0
]
x
0
,
l
') +
£
(
t
о
,
x
o
)
=
=
max<0,m
+
hn
X
[
м
Bu
,
ld
■
.
Заметим, что в силу
теоремы 1
максимум в (5) достигается на единственном векторе
l
0 e
S
(
0,1
)
, если
£
° (
t
0,
x
0)
>
0
.
Теорема 2.
Пусть £°
(
t
0,
x
0 )
>
0
, и для программного управления
u
(
e
)
(
•
)
e П
[
t
0,
T
]
имеет место равенство
x
(
T
1
,
t
0
,
x
0
,
u
’(
•
)
)
=
£
(
t
0
,
X
0
)
.
(6)
Тогда необходимо почти всюду на
[
t
0,
T
]
выполняется равенство
( X
[
T
,
t
]
Bu
(
e
)
(
t
)
,
l
°) =
=
min(
X
[
T
,
t
]
Bu
,
l
°),
где
l
0
e
S
(
0,1
)
—
вектор, доставляющий максимум в (5).
Доказательство.
Допустим, что условие (7) нарушается. Тогда существует множество
T
с
[
t
0,
T
]
ненулевой меры, на котором выполняется неравенство
XX
[
T
,
t
]
Bu(e
)
(
t
)
,
l
>
>
min(
X
[
T
,
t
]
Bu
,
1
0>,
t
e
T
Из последнего соотношения вытекает, что
T
1
Д
X
[
T
,
r
]
Bu(e
)
(
r
)
,
l0
^
dT
>
t
0
T
1
>
|
min(
X
[
T
,
t
]
Bu
,
l0^dz.
t
0
.
Подставим вектор
l
0 e
S
(
0,1
)
в правую часть
T
1
.
I
min
XX
[
T
,
t
]
Bu
(
t
)
,
l0 d^ ’
t
0
Обозначим:
x(e
)
(
t
)
=
x
(
t
,
1
0
,
x
0
,
u
(
e
)
(
•
)
)
,
t
e
[
1
0
,
T
]
.
В силу формулы Коши с учетом неравенства (8) выводим: £ (t0,x0)=max[(x()(T),l)!= i i=1
=
max
T
T
1
>X X [T, to ] x0 + J X [T ,t]bu(e)(r) dr, l0 = t0
>
X
r
Тр
[
T
,
t
0
]
x
0
,
l
') +
T
+
J
min(
Bu
,
XТр
[
T
,
t
]
l°*d
T
=
t
0
=
£
(
t
0
,
x
0
)
.
Получили противоречие. Теорема доказана.
Замечание 1. Теорема 2
выражает лишь необходимые условия выполнения равенства (6), поэтому программное управление
u
(
e
)
(
•
)
e П
[
t
0,
T
]
, определенное из условия (7), может и не обеспечить равенство (6). Выполнение этого равенства в процессе вычислений следует проверить непосредственно.
Замечание 2.
Целью введения дополнительного управления служит стремление совместить возмущенное и базовое движение точки в заданный момент времени
T
e
[
t
0,
T
]
.
Это возможно, только если
£
° (
t
0,
x
0 )
=
0
.
Однако в этом случае условия
теоремы 2
не выполняются, и условие (7) не позволяет построить дополнительное управление, осуществляющее стыковку возмущенного и базового движений точки. Итак, пусть
£
° (
t
0,
x
0 )
=
0
. Для произвольного £0
e
[
t
0,
T
]
равенства (5). Имеем: полагаем: u (t) = 0, x (t) = x (t, t0, x0, й (•)), t e [ tо, t) ]. Очевидно, что Отслеживаем величину: £ (t, x (t)), x (t) = x (t, 10, X0, й (•)), t e[t0,t0]. В случае, когда эта величина остается равной нулю вплоть до момента времени tˆ0 , момент времени tˆ0 увеличиваем в рамках промежутка [ t0, T ]. Пусть оказалось, что £° ( T, x ( T )) = 0. Тогда
=
max
J
0, max К
X
[
T
,
T
]
x
(
T
)
■
lli
T
1
■ J
min^
X
[
T
,
r
]
Bu
,
l^d
r
T
u
e
=
max 0,max
(x
(
T
)
,
l}
} =
Последнее равенство означает, что в момент времени T1 произойдет стыковка возмущенного и базового движений точки, осуществляемая управлением u(e) (•) = u (•) . В случае, когда £° (t, x (t)) становится строго положительным до наступления момента вре мени T, момент времени /0 g[t0, T ] выбира- ется из условия 0 < £ (f0, x (Fo ))< а, где а > 0 достаточно малый радиус окрестность точки pbaz ( T ) е R6.
3. Типовые геометрические ограничения на векторы управляющих параметров
В этом разделе будут приведены алгоритмы совмещения, возмущенного и базового законов движения точки при типовых геометрических ограничениях на дополнительные управления. Это случаи, когда множество
Р
с
R3
является шаром, эллипсоидом и прямоугольным параллелепипедом.
Каждый из этих случаев проиллюстрирован численным экспериментом, данные для которого совпадают с аналогичными данными из работы [1] и имеют вид: m = 100 кг, t0 = 0 c, T = 10 c, T = 1 c, k = 0.45 кг, g = 9.8M, мс x * = 2400 м, xT = 3000 м,
=
50
•
sin
(
0.000005
•
x
•
y
)
м
,
G
1
=*
x
V
У
7
y
>
g
i
(
x
)
=
=
0.001
(
x
-
1000
)(
x
-
500
)
м
}
,
G
=\
x
V
У
7
y
<
g
1
(
x
)
=
, = -0.001( x - 2500)(x - 2000) м} f xT 1 yT
V
zT
7
f
3000
м
^
^
(
xT
,
y
T
)
V
0
J
,
.
f
x
01
У
0
V
z
0
7
10
м
-
20
м
рОж
J
f
x
01
■y
0
V
z
0
7
250
м
с
-
60
м с
-
70
м
. В рамках численного эксперимента для каждого вида геометрических ограничений вычисляется величина гипотетического рассогласования £° (t0, x0 ) , строится программное управление, приводящее фазовый вектор линейного объекта в £° (t0, x0) - окрестность начала координат, вычисляется величина промаха по цели. Преобразуем формулу (5), выполнив операцию скалярного произведения под знаком интеграла во втором слагаемом. Имеем:
T
1
+
f min
J u е P t0
2
a
(
T
,
1
)
u
i
d
r
V
i
=
1
7
Здесь а (т,l), т е i = 1,2,3
S
(
0,1
)
,
Приведем результаты численного эксперимента:
– множители, которые собираются при управляющем параметре
Ui
,
i
=
1,2,3
после приведения подобных.
3.1. Случай шаров.
Множество
P
с
R3
является шаром:
'—
0.1585
"
—
0.5512
l
0 =
—
0.7257
—
0.0615
0.2254
4
0.2995
y
Pg
u
1
u
u
е
R
3
। + U + U — r . В численном эксперименте принимается
r
=
18000
м-Кг-с
2
. Из формулы (9) выводим:
£
° (
t
0
,
x
0
)
=
=
max
шестимерный единичный вектор, максимизирующий правую часть в (9); £0 (t0, x0 ) = 0.273 м — величина гипотетического рассогласования; ||x0 (T )|| = 0.2720 м — норма шестимерного фазового вектора линейного объекта в момент времени T1; A = 2.4454 м — промах по цели в конечный момент времени T .
T
1
3
2
- r [JEg (т, l) dT
t
0
i
=
1
Вектор управляющих параметров, на котором достигается минимум под знаком интеграла в (9) вычисляется по формуле
U
0 (
т
,
l
)
= -
r
а
(
т
, i
)
E g (т, l)
i
=
1
а2 (т,l) E ai (т,l)
i
=
1
g
3
(
т
,
l
)
E ai (т,l)
i
=
1
j
Одновременно формула (10) служит шаблоном для построения программного управления, переводящего фазовый вектор линейного объекта в
£
0 (
t
0,
x
0 )
—
окрестность
начала координат.
3.2. Случай эллипсоидов.
Множество
P
с
R
3
является эллипсоидом:
P Ч
u
1
u
2
u
е
R3
В численном эксперименте принимается: м • кг мктам • кг al = 20600 ——-, a2 = 18600 —, с2с2 i^M м • кг a3 = 17600 — с2
.
Из формулы (9) выводим:
£
0 (
t0
,
x
0)
=
max
<
0,max^
X
[
Tx
,
t0
]
x
0,
l^
—
T —L/e g (т, l) adт 4 Вектор управляющих параметров, на котором достигается минимум под знаком интеграла в (9) вычисляется по формуле
а
(
т
,l
)
a2
E а (т, l) al i=1
а
(
т
,
l
)
a
2
E а (т, l) al i=1 . В численном эксперименте принимается м• кг л^л^м• кг a = 17100 —, a2 = 15100 —;-, с2с2
л л л ™
м
■
кг a
3 =
14100 ——
с
2
.
Из формулы (9) выводим:
£
0
(
t
0,
x
0)
=
max
<
0, max
а
(
т
, l
)
a2
E а (т, l) ai i=1 Одновременно формула (11) служит шаблоном для построения программного управления, переводящего фазовый вектор линейного объекта в £0 (t0, x0 )— окрестность начала координат. Приведем результаты численного экспе- римента l0
'-
0.1199 '
-
0.5157
-
0.7577
0.0474 0.2118
ч
0.3138
7
шестимерный единичный вектор, максимизирующий правую часть в (9); £0 (t0, x0 ) = 0.2736 м - величина гипотетического рассогласования; ||x0 (T )|| = 0.2725 м - норма шестимерного фазового вектора линейного объекта в момент времени T1 ;
промах по цели в конечный момент времени
T
.
3.3. Случай прямоугольных параллелепипедов.
Множество
P
с
R
3
является прямоугольным параллелепипедом:
P
= )
u2
е
R
3
|u
| <
a
3, |
u
2| <
a2
, |
u
3| <
a3
*
.
'
-
П E
ki^
7
,
l
)l
a
i
I
d
т
1
0
4
i
=
1
7
Вектор управляющих параметров, на котором достигается минимум под знаком интеграла в (9) вычисляется по формуле и0 (т, l )=-
Одновременно формула (12) служит шаблоном для построения программного управления, переводящего фазовый вектор линейного объекта в
£
0 (
t
0,
x
0 )
-
окрестность начала координат.
Приведем результаты численного эксперимента: £0 (t0, x0) = 0.2646 м - величина гипотетического рассогласования; ||x0 (T )|| = 0.2677 м - норма шестимерного фазового вектора линейного объекта в момент времени T1 ;
промах по цели в конечный момент времени
T
.
Заключение В статье осуществлена стыковка возмущенного и базового законов движения управляемой точки для случая, когда на дополнительное управление налагаются геометрические ограничения в форме шаров, эллипсоидов и прямоугольных параллелепипедов. В результате произведенной стыковки дальнейшее движение точки происходило в малой окрестности базовой траектории, что обеспечивало выполнение всех сформулированных в постановке задачи наведения на цель требований к ее кинематике и точное попадание в цель. Указанный вывод подтверждается численным экспериментом.
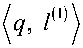
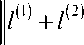
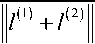
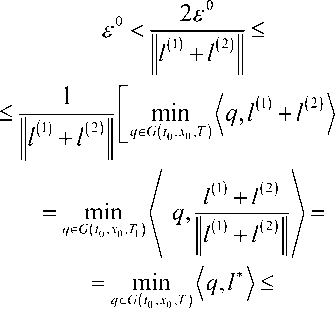
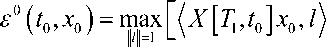
' 0.0009 "
-0.0001
l0 =
-0.9209
0.0006
0.0000
ч 0.3899 7
шестимерный единичный вектор, максимизирующий правую часть в (9);
Список литературы Приведение возмущенного движения точки на базовую траекторию при наличии геометрических ограничений на дополнительные управления
- Лутманов С.В. Построение базового закона движения материальной точки и реализующего его программного управления при наличии фазовых ограничений // Вестник Пермского университета. Математика. Механика. Информатика. 2022. Вып. 3(58). С. 25-35.
- Баландин, Д.В. Стабилизация линейных динамических объектов по измеряемому с ошибкой состоянию при ограничениях на фазовые и управляющие переменные / Д.В. Баландин, А.А. Федюков // Известия Российской академии наук. Теория и системы управления. № 5. 2021. С. 5-17.
- Велищанский М.А. Движение летательного аппарата в вертикальной плоскости при наличии ограничений на состояния // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки.2016.№ 3. C. 70-81.
- Горбачева А.В., Карамзин Д.Ю. Уточнение условий оптимальности в задачах управления с фазовыми ограничениями типа равенств и неравенств // Вестник Тамбовского университета. Серия: Естественные и технические науки. 2016. Вып. 1, т. 21. 2016. С. 40-55.
- Горбачева А.В., Карамзин Д.Ю. О некоторых классах задач управления с фазовыми ограничениями // Вестник РУДН. Серия Математика. Информатика. Физика. 2016. № 1. С.11-18.
- Болтянский В.Г. Математические методы оптимального управления. М.: Наука, 1969. 408 с.
- Васильев Ф.П. Численные методы решения экстремальных задач. М.: Наука, 1988. 549 с.
- Евтушенко Ю.Г. Методы решения экстремальных задач и их приложение в системах оптимизации. М.: Наука, 1982. 432 с.
- Кротов В.Ф. Основы теории оптимального управления. М.: Высшая школа, 1990. 429 с.
- Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1976. 392 с.
- Благодатских В.И. Введение в оптимальное управление. М.: Высшая школа, 2001. 239 с.
- Благодатских В.И. Линейная теория оптимального управления. М.: Изд-во Моск. унта, 1978.
- Габасов Р.Ф., Кириллова Ф.М. Оптимизация линейных систем. Минск: Изд.-во БГУ, 1973.246 с.
- Габасов Р.Ф., Кириллова Ф.М. Принцип максимума в теории оптимального управления. Минск: Наука и техника, 1974. 272 с.
- Красовский Н.Н. Теория управления движением. М.: Наука, 1968. 476 с.
- Красовский Н.Н. Игровые задачи о встрече движений М.: Наука, 1970. 420 с.
- Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1973.456 с.
- КиселёвЮ.Н. Линейная теория быстродействия с возмущениями. М.: Изд-во Моск. ун-та, 1986. 106 с.
- Уонэм М. Линейные многомерные системы управления М.: Наука, 1980. 376 с
- Лутманов С.В. Элементы выпуклого анализа и методы оптимизации: учеб. пособие / Перм. ун-т. Пермь, 2018. На электронном носителе 180 с. ISBN 978-5-7944-3114-8. https://elis.psu.ru/ident/978-5-7944-3114-8.


