Признаки устойчивости и неустойчивости экстремальных поверхностей вращения

Постановка задачи. Пусть M — n-мерное связное ориентируемое многообразие класса C ² без края. Рассмотрим гиперповерхность M = (M, u) без края, полученную C ² -вложением u : M ^ R n⁺¹ , и C ² -гладкую функцию Ф : R n⁺¹ ^ R , С ^ R n⁺¹ , Ф( - £) = Ф(£). Если обозначить через £ поле единичных нормалей к поверхности M , то для любой C ² -гладкой поверхности M определена величина

F(M) = I Ф(С )

d M ,

M

которая не зависит от выбора нормали ξ. Функционал (1) будем называть функционалом типа площади.

Основной объект данного исследования — экстремали функционала (1). Заметим, что при Ф(£) = 1 ими являются минимальные поверхности.

Цель работы: получение признаков устойчивости и неустойчивости экстремальных поверхностей M .

О подходах к решению подобных задач. Под устойчивостью будем понимать знакоопределенность второй вариации функционала типа площади при бесконечно малых деформациях поверхности. Напомним, что для минимальных поверхностей устойчивость означает положительную определенность второй вариации объема. В рассматриваемых нами случаях знак второй вариации для локальных вариаций может быть как положительным, так и отрицательным, в зависимости от свойств функции Ф(£). Из этих соображений понятие устойчивости определяем как способность второй вариации сохранять знак на множестве всех допустимых вариаций, подобно работе [4] для поверхностей нулевой средней кривизны в искривленных лоренцевых произведениях. Поэтому для некоторых функций Ф(£) следует рассматривать задачу на минимум функционала F(M), а для некоторых — на максимум.

Устойчивость подмногообразий нулевой средней кривизны в римановых многообразиях изучена довольно глубоко. Ей посвящены работы Х. Барбоса и М. до Кармо, Х. Лоусона, А.В. Погорелова, Дж. Саймонса [10], А.А. Тужилина [7], А.Т. Фоменко [8] и др. Для минимальных поверхностей в 3-мерном евклидовом пространстве явление неустойчивости рассматривал еще Г.А. Шварц в XIX веке. В псевдоримановых многообразиях задачи устойчивости стали решаться сравнительно недавно, но и здесь есть интересные подходы к решению и важные результаты.

Стоит заметить, что исследования проводятся различными методами. Приведем некоторые из них. Х. Барбоса и М. до Кармо показали, что ориентируемая минимальная поверхность в R ³ , у которой площадь образа гауссова отображения меньше, чем 2п, устойчива. До Кармо и Пенг дали обобщение проблемы Бернштейна в терминах устойчивости: плоскость — единственная полная устойчивая минимальная поверхность в R ³ , а в пространстве Лобачевского существуют однопараметрические семейства таких поверхностей. В работах А.А. Тужилина такие семейства подробно описаны с помощью понятия «индекс», а индекс минимальных поверхностей вращения в пространстве Лобачевского исследуется методом рядов Фурье, например в [7]. Исследования индекса компактных и некомпактных минимальных поверхностей и определение устойчивости можно также найти и в работах Х. Лоусона, А.Т. Фоменко, А.В. Тырина, Д. Фишер-Колбри. В работах В.М. Миклюкова, В.А. Клячина, В.Г. Ткачева применяется емкостная техника для определения устойчивости поверхностей.

Пусть V — C ² -гладкое векторное поле, определенное в окрестности поверхности M , такое, что V | м = h^, где h Е C 01 ( M ), £ — поле единичных нормалей к поверхности, при этом предполагается, что интегральные кривые поля V лежат на прямых линиях и вдоль них выполнено | V | = const.

Ясно, что если поверхность M вложена, то любое векторное поле V = h - £, заданное вдоль M , можно продолжить в некоторую окрестность M так, что будут выполнены сформулированные выше условия. Заметим, что согласно работе [10] вторая вариация не зависит от выбора продолжений.

Пусть U ( M ) — окрестность поверхности M , в которой определено поле V и однопараметрическая группа локальных диффеоморфизмов g t (x) : U( M ) ^ R ^{n +1} , порожденная векторным полем V. То есть g t (x) есть решение задачи Коши:

^dgt, ⁽, ^{x )} = V(g t (x)), g t (x) | t =o = x. dt

Положим M t = g t ( M ). Ясно, что M o = M .

Определение 1. Поверхность M является стационарной, если первая вариация функ- ционала (1) равна нулю, то есть d /»«) dMt

M t

= 0.

t =0

Определение 2. Стационарная поверхность M будет устойчива , если вторая вариация функционала (1)

d ²

»2 / ^ф« ^{) d} M t

M t

t =0

знакоопределена при всех бесконечно малых деформациях M _t поверхности M , иначе поверхность M — неустойчива .

Замечание. В случае когда вторая вариация стационарной поверхности локально знакоопределена, то есть вариации с малым носителем дают одинаковый знак, будем называть поверхность экстремальной . Далее будут рассматриваться только экстремальные поверхности.

В работе [3] была доказана следующая теорема.

Теорема 1. Поверхность M класса C ² является экстремалью функционала (1) тогда и только тогда, когда

n

Е k i G(E i ,E i ) = 0.                               (2)

i =1

Экстремальная поверхность M устойчива (неустойчива), если для любой функции h(x) G C q ( M ) знакоопределена (не является знакоопределенной) квадратичная

форма

G( V h, V h) - h ² ]Т k i² G(E i , E i ) i =1

d M ,

где G — квадратичная форма, соответствующая матрице

G ij =       + ^ ij ^(ф - ^ D^ ^ ⁾ⁱ

∂ξ i ∂ξ j

δ _ij — символ Кронекера, k _i — главные кривизны, а E _i — главные направления поверхности M .

Замечание. Теоремы и следствия, представленные в данном пункте, были опубликованы без доказательств в [6].

Далее будем рассматривать функционал специального вида

f ( M ) = I Ф«п ₊ 1 )а м , M

где d M — элемент площади на C ² -гладкой поверхности M С R n +1 , заданной радиус-вектором

R(t,6) = (t,r(t)p(6)),

6 Е S n ^{- 1} , р(6) — радиус-вектор сферы S n ^{- 1} , t Е (a,b) С R , r(t) — C ² -гладкая функция на (a, b), ф+1 — координата единичной нормали к поверхности M .

Обозначим т = £ n ₊₁ = — r(t)/ ф 1 + r ² (t), тогда

Ф (т ) = dф/dт,

Ф ‘(т) = d²ф/dт ² , r = dr(t)/dt, r = d ² r(t)/dt ² .

Пусть

B(t) = ф‘(т)/ ((1 + r2(t)) фф(т) + ф(т)r(t)/^1 + r2(t)^ ^ , тогда справедлива следующая теорема.

Теорема 2. Поверхность M , заданная радиус-вектором (5), является экстремальной тогда и только тогда, когда

r(t)r(t)       n — 1

1 + r ² (t)    B (t) + 1

Экстремальная поверхность M устойчива тогда и только тогда, когда функционал

h t 2 (t,6)

1 + r ² (t)

( B ( t ) + 1) +

\ D e h(t,6 )|² -      h ² (t,6)      (n — 1)(n + B(t))

r ² (t)        r ² (t)(1 + r ² (t))      B(t) + 1

_x ( Ф(т) + Ф ^(т >’ ^- < ^t > d M v' ¹ V+Ttt®

знакоопределен в классе липшицевых функций h : R ^{n +1} ^ R таких, что h Е C q ( M ) .

Доказательство. Заметим, что теорема 2 является следствием теоремы 1. Поэтому ее доказательство заключается в том, чтобы записать (2) и (3) с учетом (4) и (5). Для этого нам потребуется выписать выражения главных кривизн и главных направлений поверхности, заданной радиус-вектором (5).

Запишем I и II квадратичные формы поверхности M .

Так как

\Rt\2 = 1+ r2(t), \Rei\2 = r2(t)p6iP)6j, то первая квадратичная форма

I = (1 + T-2(t))dt2 + r2(t)p)0i pigj d6id6j = (1 + r,2(t))dt2 + r2(t)d62, где d62 = p-oip-gj d6id6j — элемент длины для Sn 1, i, j = 1, n — 1. Вторая квадратичная форма n-1

II = boo dt2 + 52 boi dt d6i + 52 bij d6i d63, i=1              i<=j где

b 00

b 0 i b ij

ξ

№, < ⁾ = ( ⁽⁰ ,r ⁽ t)p), ( - ryw ¹ + r²^), p/V ^{1 +} r ^{2 (t) ) )} = ^rU ^, 1 + r ² (t)

\ R t9 i , £ ⁾ = ( ^(0,rp 9 i ), ^{( - r(t)/} V¹⁺" ^r’²⁽ t ^y2_^Pb/¹⁺ r ^(ty ) l = ^0,

( R 9 i 9 j , £ ⁾ = ( ^(0,rp 9 i ^p 9 i 9 j ^{y (-r(t)/}V ^{1 +} r 2 ^(t) , P/ V ^{1 + r} 2 ^{(t) ) )} =

r(t)

n.—:—/ _A \^p 6 i^p 6 i 6 j , ^p) ,

V 1+ r (t) r t \ 1 ■ r2(t), p/V1 + r2(t)).

Таким образом,

II = , r ^(t)      dt 2 + , ’'^      d^,

V 1 + r' ² (t)         V 1 + r' ² (t)

где dθ ² — вторая квадратичная форма для S ^{n- 1}

.

Применяя формулы из [2], находим главные кривизны ki = r(t)/(1 + T-2(t))3/2, k, = -1/r(t)y1 + r2(t), i = 2,n, и главные направления поверхности M

E 1 = R , / \ R , \ = (1/ ^ 1 + r ² (t) , rWp/^ + r ² (t) ) ,

E , = R , i / \ R » i| = (0, p „ , J\p _{e i} \ ).

Для подстановки в (3) требуется вычислить Vh в метрике поверхности M. Напомним формулу n-1   ∂h

(Vh) = ^g3   , где i = 0,n - 1, j=0   ∂xj и ||g,j|| — обозначение для матрицы коэффициентов первой квадратичной формы, а ||gij|| — обратной к ней матрицы.

Далее вычислим координаты градиента функции h о _ у1 noj dh _ оо dh _ h't(t, 9)

(  ) = j=0 g dXj = g dX0 = Г+Т2Й, v^ У dh         ij dh 1 V^ ~iidh(t,^)    1

^(Vh) = zLg ’-g^ = Hgj-g^ = -2 T.^g,-§e7^ = 7^(D)l'^t,7^y,,, i = 0.

j =0    ^{∂x j}    j =1 ^{∂x r} j =1      ^{∂θ ij      r}

Обозначая вектор с координатами (Dh(t, 6)) ^г через D g h(t,9), получим координатную запись вектора градиента

/ hW)   ^D « hfc⁹ ) А

^{V h(<} , ⁹⁾ =(TTZ:2(t), ^2Й“)'

Отсюда нетрудно видеть, что квадрат модуля градиента будет иметь вид

|Vh(t,9)\2 = h2 (t,9)/(1 + At)) + \Dgh(t,9)|2/r2(t), так как |Vh|2 = n£ gij ((Vh))2.

j =0

Перейдем к вычислению требуемого скалярного произведения векторов

/тлл           ^?;(t) ^ ^(т )

С иф, f > —--.

' ^v’V1 + - ^{; 2} (t)

и найдем значения матриц D ² ф и G на векторах E i и V h, координаты которых записали выше,

мы

G(E i ,E i )

D²ф(E 1 ’E 1 )= ^Ф^^Т)- , D²ф(E i ,E i ) = 0,i = 2,n, 1 + r ² ( t )

^Ф ' ^Тт )    ,           ,   ^ф‘ ^(т)r(t)    ГЧТ7                   ,   ^ф‘ ^(т)r(t)

T~^77\ ^{+ ф(т}) ⁺-- /тД^ШГ’ ^G(Ei , Ei) = ^ф(т) ⁺-- и , -o/.x ,

1 + r ² (t)             Д1 + r- ² (t)                            V1 + r' ² (t)

G( V h’ V h) = ^ф " ) ^т )^ + (1£MU ^{v 7}     (1+ r ² (t)) ²        1 + r ² (t)

I D ₆ h(t,Q) [ 2 r ² (t)

ф'(т )r(t)

Дф(т) +,      /

Теперь подставим посчитанное в равенство (2) и получим уравнение экстремалей поверхности M , заданной радиус-вектором (5).

Так как все k i при i = 2, n равны, и для G(E i ,E i ) ситуация аналогичная, то равенство (2) примет вид

n

n

52 k i G(E i , E i ) = k i G(E i , E i ) + (n - 1) 52 k i G(E i , E i ) = 0.

i =1

i =2

Таким образом, полученное уравнение экстремалей

r(t)      ( Ф " (т )      ф( )

(1 + r 2 (t)) ³ / ²   1+ r ² (t)

^Ф( Т ^)r(t)

V 1 + r ² (t)

-

n - 1

r(t) У1 + r ² (t) преобразуем, сократив на £1 + r ² (t),

(ф(т ) + ф ‘ ^(т > ^r

V^{1 + r} 2 ^(t)

r(t)

1 + r ² (t)

(

^Ф ‘ ⁽ т ) 1 + r 2 (t)

^ф'^(т)r(t) ^ n ^{- 1}

^{+ ф(т} > ⁺     .   .) - -^г Д^т’ +

ФЧг У г -) )^

V 1 + r* ² (t)

)0-

а затем выразим r(t)

n -

r(t)

r(t)

1 Гф<т)+jr 2™

^{1 + r} 2 ^(t)

ф"^{( т} ) ,          , ^ф'( ^т )’■(<)         ’

Г+72Й + ^ф(т)+ _c .

вынесем в знаменателе за скобки ф(т) + ф(т)r’(t)/\/1 + r2(t) и подставим введенное ранее обозначение B(t). Получим n — 1               1+ r 2(t)                   n — 1    1+ r 2(t)

r(t) _________________ ^ф ‘‘ ^(т ) _________________+ 1 B(t) + 1 r(t)

(1+ r 2 (t)) U) + -ф’^)

V         V ^{1 + r} 2 ^(t)

что и дает нам заявленное в теореме уравнение экстремалей

r(t)r(t)        n — 1

-

1 + r ² (t)    B (t) + 1

Далее приступим к вычислению второй вариации экстремальной поверхности M , заданной радиус-вектором (5). Подставим посчитанные выражения в (3) и преобразуем полученный интеграл:

G( V h, V h) — h ² ]T k-G(E i , E i )

i =1

d M =

Ф"(т )

h2M) (1+ r ² (t)) ²

h ² (M)

⁺ (1+ r ² (t) ⁺

D h(W r ² (t)

^ф'^{(т )r(t)} Д^ф(т)+,)

-

b 2^             ^r(t)     У 2 ( ^ф ‘ ^(т )               ^ф(т rt \.

^{—h (<,6 )}Д 1 + r 2 (t )H ( 1+7 2 (0 ^{+ ф(т) +} ,      • ■ ⁺

+ (n — 1) ((     - ^{— 1}      у Г ф₍т) + ^ф ‘ ^(т)r(t) ^) d M .

r(t)—1 + r- ² (t)                 — 1 + r- 2 (t)

Возведем в квадрат выражения при h2 и сгруппируем слагаемые, стоящие при ht2 , получим f J ht2(t,0) / ф‘‘(т)                 ф‘(т)r(t)

M (ттт2й (тт72й + ^{ф ( т )+}_; t Д

I D« '=(«■<       x , Ф ‘ (т)-‘(t) \

⁺ ^2й“ ф^{(т) +} тг+ж) ^—

1 2/. m f      ^r(t)2       f ^Ф ‘‘ ^(Т) ,         , ^Ф ‘ ^(Т)r,(t) У ,

^{—h (t,6)} ((1 + r 2 (t)) 3 (1+72 (0 ^{+ ф(т} ) ⁺ vTTrW) ⁺

+ (n — 1) (      ¹ „ „ ф(т) + ^ф(т)r(t > ^U dM.

r ² (t)(1 + r- ² (t))        ⁷    V 1+ r ² (t)

Теперь подставим в интеграл выражение r(t) из (10):

h t 2 (t,6)

1 + r- ² (t)

(

^ф ‘‘ ⁽ Т )

1 + r^{, 2} (t)

ф'(т )r(t)

^{+ ф(т )+}-mw Г

I D , h(t,< /         ф'(т )r(t)

+ ^t)” 1Ф(Т)+ „     • )

^^^^^^^^^r

- h²(t,Q)

¹ / ^ a ,    ^Ф(т)r(t)

ф(т) +(1 + r

V        T ^{1 + r 2 (t)}/

Ф"^(т ) , x , ^{Ф(т )r(t)} ■             ^Ф(т >+ ..          .

/

X

X

(1 + r ² (t)) 3

^Ф ‘ ^(т)    ,         , ^ф(т)r(t)

I r+?w ^{+ Ф(т)+} .      - p

+ (n - 1) f ¹    „ фф(т ) + «Й ) П dM.

r ² (t)(1 + r ² (t))       ⁷ V 1+ r ² (t)

Упростим выражение при h ²

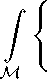
h t² (t.6)

1 + r ² (t)

Ф"(т) ж Я W

^ Г+7$й ^{+ Ф(т ) +}

^Ф( т ⁾T'^(t)

V1 + r^{1 2} (t)

)

+

I D, h(t,») | ² C . ,  ф ‘ (т W1

⁺ ^2(i^ ^ф(т)+_;. t )

-

-

h²(t,Q) r ² (t)(1 + r^{, 2} (t))

⁽ n ^{- 1) 2} ^^{Ф (} т) ⁺

^{ф (} т ^)r(t)

V 1 + r" ² (t)

У

Ф'(т ) 1 + r- ² (t)

^Ф( т ^)r(t)

V 1 + r ² (t)

+

^{+ (n - 11} (^{ф(т) +} ;^фЙ⁽|))) }^{d M} =

M

^ф ‘ ‘ ⁽ т )

1 + T- ² (t)

Ф(т )r'(t)

^{+ Ф(т )+}       г

I D , h(t,e)P (          ф ' (т )r(t) A ,

⁺^2й~ ^{ф(т) +} TT+Wj) ^{- h(t} , ⁶^

n - 1

------------- X r2(t)(1 + r-2(t))

Ф(т )r'(t)

^{X ф(т)+} vTTRtj)

⁽ n ^- 1) ^^{Ф (} т) ⁺

^{ф (} т ^)r(t) V 1 + r ² (t)

)

Ф ‘ (т ) + r" ² (t)

^Ф( т ^)r'^(t)

V1 + r’ ² (t)

+1

d M .

/

ф,(т)r(t)

Вынесем за скобки ф(т ) +--.        :

1 + r- ² (t)

M

htXM) 1 + r- ² (t)

___________________ ^ф ‘‘ ⁽ т )

^{(1 +} r²^)) ^^ф(т ) ⁺

^ф( т ^)r(t)

V ¹ + r ² (t)

Г)

+

l D _e h(t,9) l ² r²(t)

^^^^^^^^^r

^^^^^^^^^r

h ² (t, 0)

n r 1

r ² (t)(1 + r ² (t))

n r 1

___________________ ^Ф ‘‘ ⁽ т)

^{(1 +} r ^{- 2 (t)) ффф} ) ⁺

^ф,( т ^)r(t) V 1 + r- ² (t)

-----+ 1 ) ^+l

х

х

(ф (т) + ф ‘ ^{(т )r(t)} ) d M

V'  УТ+Т2Й и, учитывая, что

^ф ‘ ⁽ т )

^{(1 +} r ^{2 (t)) ф}Ф( т ) ⁺

^Ф( Т ^)r'^(t)

V ¹ + r ² (t)

J = B(t),

получаем выражение для второй вариации функционала (4) в классе экстремальных поверхностей вращения f I hi2(.M)         , n , Id)h(t,«)|2    .2,,,,.

Г+^:2Й ( ^{B +} 1> ⁺ r 2 (t)     ^{— h 0)}

M

n r 1

r ² (t)(1 + r ²

/ n - 1

(0)     B^: ■ +. ■ ^X

ф,(т )r(t)

X ф(Т) +--.            :

V ^{1 +} r ^{2 (t)}

f / h t ² (t, ⁰ )        ^va^VD ) h(t,<

J j Г+?2Й ^{(B(t) + 11 +}    r 2 (t)

M

^^^^^^^^^r

^^^^^^^^^r

h²(t,0')     (n — 1)(n + B (t))

r ² (t)(1+ r ² (t))      B (t) + 1

+   ^фч.т ^)r(t) A d M ,

V ^{1 +} r ^{2 (t)}

которое полностью совпадает с (7). Что и требовалось доказать.

Следствие 1. Поверхности, заданные радиус-вектором (5), при ф(£ _п+1 ) = 1 являются экстремальными тогда и только тогда, когда выполнено равенство

r(t)

n r

^^^^^^^^^r     ^^^^^^^^^^^^^^^^^^^^^^^^^^B

1 + r ² (t)     r(t)

- =0,

и совпадают с классом минимальных поверхностей [1].

Пусть

a(t) = (ф(т) + ^{№) r(t )} ) , r ^(t)     (B (t) + 1),

1+ r²^) V 1 + r ² (t) ' ' '    ’

в п (t) =

^ф ‘ ^(т w) ⁾⁺_c.

1         (n — 1) (n + B (t))

r(t)^1 + r ² (t)      B (t) + 1

Следствие 2. Экстремальная поверхность M , заданная радиус-вектором (5), является устойчивой тогда и только тогда, когда знакоопределен функционал

/ ^{a(t)h ‘ ^{2 (t)} a

— e n (t)h ² (t) } dt

в классе липшицевых функций h : R ^ R таких, что h(a) = h(b) = 0.

Доказательство. Проведем доказательство в два этапа. Сначала покажем, как получили функционал (11), а затем проведем непосредственное доказательство устойчивости в обе стороны.

Функционал (7) приводится к заявленному в следствии виду (11) в несколько действий. Выпишем функционал (7)

h t² (t,g) (B(t) + 1) .

1 + 7'2 (t)

D h(t,0) | ² -      h ² (t,0)     (n — 1)(B(t) + n)

r ² (t)         r ² (t)(1 + r^{, 2} (t))        B (t) + 1

x (Ф(т) + ф ‘ ^{(т)r(t )} ) d M .

Л+^Й

Очевидно, что для него верно неравенство

M

h t² (t,6) (B(t) + 1) 1 + r- ² (t)

—

h²(t,&)     (n — 1)(B (t) + n)

r ² (t)(1 + r^{1 2} (t))      B (t) + 1

x

x ^^{ф (т} ) ⁺

^Ф ‘ ⁽ т ^)r(t) ^1 + r ² (t)

d M .

Из выражения I квадратичной формы имеем d M = r(t)y1 + ?' ² (t) dtd9, поэтому

Q >

b

J a(t) / a          Sn-1

h t² (M) d0

— 8 „ (t) У

_S n - 1

h ² (t,0) d0

dt.

Пусть

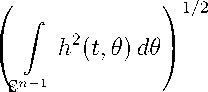
= ^z(t) ,

тогда

z ² (t) =

_S n - 1

h ² (t,0) d0,

2z ‘ (t)z(t)=2 I h(t,9)h' t (t,9) d9,

_S n - 1

применяя неравенство Коши — Буняковского, будем иметь z‘2(t) < 2 (t) j h2(t,9) d9 j h'2(t,9) d9 ^ z‘2(t) < j h‘2(t, 9) d9.

_S n - 1

_S n - 1

_S n - 1

Таким образом, получаем

Q >  I | a(t)z ‘ 2 (t) - e n (t)z 2 (t) } dt. a

Переходим ко второму этапу доказательства. Если функционал (11) будет знакоопределен для всех z(t), то непосредственно из определения 2 будет следовать устойчивость. Например, если при a(t) > 0, то из неравенства Q >  J { a(t)z ‘ ² (t) — в _п (t)z ² (t) } dt >  a

• > 0 следует устойчивость поверхности.

В обратную сторону, если поверхность устойчива, значит вариации поверхности в направлении векторного поля не меняют знака второй вариации, то есть имеем ее знакоопределенность, а следовательно, и функционала (11). Например, если мы полагаем, что a(t) > 0, то будет положительная определенность второй вариации функционала, а следовательно, и функционала (11).

Что и требовалось доказать.

Следствие 3. Экстремальная поверхность, заданная радиус-вектором (5), является устойчивой, если a(t)e n (t) <  0.

Доказательство. Следствие становится очевидным, если применить к формуле второй вариации поверхности определение 2.

Заметим, что в случае n = 2 поверхность M задается радиус-вектором

r(t, 9) = { t, r(t) cos 9, r(t) sin 9 } .

Следствие 4. Поверхность M , заданная радиус-вектором (12), является экстремальной тогда и только тогда, когда выполнено одно из уравнений

^r(t)r(t) _      1      ₌

1 + r ² (t)     B (t) + 1

или

М(^ф‘^(т ) ^T ^r( twy ^{+ ф(т} ’) ,/■ • ■!   ^|:

Доказательство. Легко видеть, что первое из уравнений экстремалей получается при подстановке в (6) n = 2. Второе проверяется непосредственным дифференцированием.

Пример 1. При ф(^ _п+1 ) = 2^ 2+1 — 1 для функционала (4) класс экстремальных поверхностей соответствует классу максимальных поверхностей в пространстве-времени Минковского R ₁ ^{n +1} , которые устойчивы и глобально максимизируют площадь в R ₁ ^{n +1} (см. [4]). Вычисление уравнения экстремалей и доказательство глобальной устойчивости для случая n = 2 было проведено автором в [5].

• 3. Признак устойчивости и неустойчивости

Пусть sup a(t)e n (t) = v ² < + то , тогда справедлива следующая теорема. t e ( a,b )

Теорема 3. Пусть экстремальная поверхность M задана радиус-вектором (5). Для положительных функций a(t), e n (t) поверхность M является устойчивой, если

b dt

< nv,

J a(t)

a и неустойчивой, если

b jen(t)dt > nv.

a

Замечание. Теорема 3 была для случая n = 2 доказана автором в статье [5], а в данной формулировке опубликована без доказательств в [6].

Доказательство. Рассуждая также, как в доказательстве следствия 2, замечаем, что квадратичную форму (7) можно оценить снизу некоторым функционалом, то есть

h t² (t)

1 + r ² (t)

^(B(t) + 1) -

h ² (t)       (n — 1)(n + B (t))

r ² (t)(1 + r ² (t))       B (t) + 1

I -

ф(т )r(t)

^{- ф( т)+},       )

b dM > Шп—11 (zt2 (t)a(t) — z2(t)en(t)) dt,

a где шп-1 — площадь (n — 1)-мерной сферы и ф‘(т)T(t)          r(t)

^a(t) = ^{ф(т 1 +} ;■■) -■■ ^{(B(t) +1)1}

^e n ^(t) = R^(t ) +

^Ф( т ^)T(t)

\         1       (n — 1)(n + B (t))

r(t) T 1 + r- ² (t)       ^{B (t)} + ¹

T 1 + r- ² (t)

Из условия на функции sup a(t)en(t) = v2 следует, что a(t)en(t) < v2. Тогда справедливо неравенство j |a(t)z‘2(t) — en(t)z2(t)| dt ^ j |a(t)z/2(t) — v^t) } dt.

b

b

a

a

Заметим, что для устойчивости экстремальной поверхности вращения достаточно

/{a(t)z ‘ ² (t) — ^ i z^^l dt >  0, ^a(t)

a или, что то же самое,

b

J a(t)z'2(t) dt a-------------^ 1.

b

/ v2^2 dt a(t)

a

Сделаем замену в интегралах и рассмотрим их отношение.

Пусть

t

y(t) = I du/a(u), t E [0,b — a], тогда dy = dt/a(t) и zt = zyyt = z‘y/a(t), и отношение (13) принимает вид

b

I a(t)z ² (t) dt a

b

[ ^ dt a(t)

a

y ( b )

J z ’ y ⁽ y) dy

• 1    УЛ________

V ² У ^{( ь )}

• I    z^{2 (} y) dy y ( a )

.

Применяя к (14) неравенство Виртингера [9, § 7.7], получим

y ( b )

I z'yWv  /

\-2

y ^{( a )} _> y^{( b )}

I z^{2 (} y)dy

y ( a )

π

b

/ dt/^t)

.

Далее, сопоставляя (13) и (15), будем иметь неравенство для устойчивости поверхности вращения:

b j a(t)z2(t) dt a

b

/ ^V24(l dt a(t)

a

y ^{( b )}

I z ’y Ы dy

• 1    У И________

• V ² y^{( b )}

I z²(y) dy y ( a )

> -77 V

\-2

П

b

/ dt/a(t)

> 1,

b

I dt/a(t) <  nv.

a

Так как для доказательства неустойчивости достаточно предъявить хотя бы одну функцию h, для которой нарушается знакоопределенность второй вариации, то допустим, что в функционале (7) функция h(t, в) = h(t), тогда он принимает вид

Ш п -11 ( h t 2 (t)a(t) - h ² (t)B n (t) ) dt. a

Так как a(t)B _n (t) С v ² , то справедливо неравенство

b j |a(t)h,2(t)

a

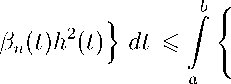
v ² h ‘ ² (t) B n (t)

-

вп№² (t) ।

dt.

Таким образом, чтобы экстремальная поверхность вращения была неустойчивой, достаточно, чтобы существовала функция h Е C01(a,b) такая, что или

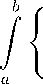
v ² h ’ ² (t) в п (t)

— в _п (t)h ² (t)    dt С 0

b v ² h ‘ ² (t)

a B n (t)

dt

b

J B n (t)h²(t) dt a

С 1.

Рассмотрим функцию h, заданную равенством

h(u) = sin

/

n

I

u          \

J B n (t) dt

a

b

J B n (t) dt a

Тогда

b

I h^ dt Bn(t) ν2 ba вп (t)h2 (t) dt a

= v ²

b j 8„(t)

a

cos ²

π

·

t

J вп (u) du

П a

J ^B n ^{(t) dt}

dt

₍ J e n (t) dt a

/

b

I B n (t) sin ²

a

t

J в п (и) du

π ^a

J e n (t) dt a

dt

/

/

= v ²

b j Bn (t) a

1 + cos

2n

π

, J ^en⁽t) dt a

·

b

^У    / B n (t)

a

/

1 — cos

/

2n

t

J B n (u) du a

b вп (t) dt a

t

J B n (u) du a

b вп (t) dt a

dt

dt

= v ²

П

, J ^en⁽t) ^dt a

/

,

a

cos

t

J в п (u) du

J P n (t) dt

dt = 0.

Следовательно, при выполнении условия

b jвп (t)dt > nv

a выполнено (16), что означает, что поверхность будет неустойчива.

Теорема 3 доказана.

Для иллюстрации полученных в теореме 3 результатов приведем следующий пример. Пример 2. В работе [5] было установлено для случая n = 2, что экстремалями функционала (4) с функцией

^ф(т ) = ^{т (t)}

^{т ( t )}

C i + C j (1

^{т ( t} 0 )

- т 2 (t)) ⁽ P ^{-2) / 2} т ^{2 (t)}

где т = < 3 , C = (Ф(т (t o ))T(t o ) - ф(т(t o )))(1 — T ² (t o )) ^{(2 p ) / 2} , C = ф(т(t 0 ))/T (t o ), являются p -минимальные поверхности, класс которых был впервые указан В.М. Миклюковым и исследовался в работе В.Г. Ткачева [11].

Такие поверхности характеризуются тем, что функция x ₃ = f (x ₁ , x ₂ ) в метрике поверхности M является p -гармонической, то есть удовлетворяет дифференциальному уравнению div( |V f | ^{p- 2} V f) = 0 в метрике p-минимальной поверхности M .

На основании теоремы 3 можно заключить, что p -минимальная поверхность вращения устойчива на интервале (t ₀ ,t), определяемом из неравенства

t

-

t o <  п

(p—JVp r o C P ^{- 1}

C o =

r' ^{2 (t} o ^{) + 1} . _f ^^^T\to), t^^ f)

r ( t ) = r o ,

и неустойчива на интервале, который находится из неравенства

r ^{( t )}

r ( t 0 )

dr p-1

>π

r ² (t) У C o r p^{- 1} (t) - 1

Подробные вычисления приведенных неравенств можно найти в работе [5].

¹ Работа выполнена при финансовой поддержке гранта РФФИ (проект № 11-01-97021-р_поволжье_а).