Признаки устойчивости разностных уравнений Вольтерра

Рассмотрим линейное разностное уравнение типа Вольтерра xn = xn-1 -^Lasxn-s ’     n =1,2,--                                 (1)

s = 1

где a s e R , a s >  0   ( s = 1,2,...).

Начальное условие x 0 однозначно определяет решение уравнения (1).

Нулевое решение уравнения (1) называется устойчивым, если

Vs > 0 35 > 0 (Vx0 |x0| < 5^Vn > 0 |xn| < s)

Нулевое решение уравнения (1) называется асимптотически устойчивым, если он устойчиво и lim x n = 0 для любого решения ( x n ) уравнения (1). n ^w

Уравнение Вольтерра (1) является бесконечномерным аналогом разностного уравнения

k xn = xn-1 — ^asxn-s ,                                       (2)

s = 1

где a s e R , a s >  0 ( 1 <  s <  k ) .

Для уравнения (2) известны следующие признаки асимптотической устойчивости [1].

Теорема 1 . Если a s >  0 ( 1 <  s <  k ) и

0 <У----- a s -----< 1,

^s = 1 2sin--------- 2(2 s - 1) то нулевое решение уравнения (2) асимптотически устойчиво.

Теорема 1 является многомерным обобщением известного результата Левина и Мэя [2].

Теорема 2. Если a s >  0 ( 1 <  s <  k ) и

П

⁰ < У sa s <7 ,                                     ⁽⁴⁾

s = 1         ²

то нулевое решение уравнения (2) асимптотически устойчиво.

Признак устойчивости теоремы 1 сильнее признака теоремы 2. Теорема 1 в некотором смысле не может быть улучшена [1].

Цель работы - получить аналоги теорем 1 и 2 для разностного уравнения Вольтерра (1).

Производящей функцией числовой последовательности xn (n > 0) называется ряд вида да

X(z) = Z(xn) = У xnzn , n=0 где z e C.

Сверткой двух последовательностей x_n и y n называется последовательность вида

Xn ° Уп =   Xn-sys = У Х$Уп-s • s=0

Производящая функция свертки двух последовательностей имеет вид

Z ( ^X n ^yy_n ) = ^{X ( z} ) ^{y ( z} ) .

Теорема 3 . Пусть выполняются условия:

• 1)    существуют действительные числа M >  0 и q e ( 0;1 ) такие, что для всех n e N выполняется a n <  Mqⁿ ;

да

• 2)    все нули функции g ( z ) = 1 - z + ^ a n z n расположены вне единичной окружности | z | = 1.

n = 1

Тогда нулевое решение уравнения (1) асимптотически устойчиво.

Доказательство . Пусть последовательность ^x n ( ^П >  0 ) является решением уравнения (1). Значит,

X 1 = x ₀ - a 1 x ₀ , x ₂ = X 1 - ( a 1 x 1 + a ₂ x ₀ ) , x ₃ = x ₂ - ( a 1 x₂ + a ₂ X 1 + a ₃ x ₀ ), ...

Умножим обе части первого уравнение на z, второго - на z2, третьего - на z3 и так далее. Сложим полученные равенства и добавим к обеим частям x0 . Согласно определению производящей функции (5) получим да

X ( z ) = x ₀ + zX ( z ) - X ( z ) У a n z n .

n = 1

Тогда x (z)=—xда—.                        (7)

• ^{1    -} z + E a n z n

n = 1

Обозначим функцию да g ⁽ z ) = ^{1 -} z + У a n z n .                                     ⁽⁸⁾

n = 1

Из условий теоремы следует, что функция g ( z ) является аналитической в круге | z | = R , радиус которого R больше единицы. Тогда из (7) следует, что X ( z ) раскладывается в степенной ряд по степеням z с радиусом сходимости больше единицы. Следовательно, уравнение (1) экспоненциально, а, значит, и асимптотически устойчиво при любом начальном условии x ₀ . Теорема доказана.

В работе [1] доказаны следующие вспомогательные леммы.

Лемма 1 . Для любого числа со e ( 0; п ] существует число m e R , такое, что для всякого s e N

sin

п

2 ( 2 s - 1 )

sin ( m - s ) to

■ to     (      1A sin —cos m — to

2     I      2 J

Лемма 2 . Для любого числа s g N , такое что всякого s g N

2sin

>—

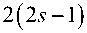
2 s

Теорема 4 . Пусть выполняются условия:

• 1)    существуют действительные числа M >  0 и q g ( 0;1 ) такие, что для всех n g N выполня

ется a n <  Mqⁿ ;

да

п

2(2 s - 1)

< 1.

• 2)    0 < Z---

• s=1 2sin

Тогда нулевое решение уравнения (1) асимптотически устойчиво.

Доказательство . Предположим, что условия теоремы выполняются и существует нуль z функции g ( z ), такой, что | z ₀| <  1.

1. Рассмотрим случай |zo| = 1. Пусть существует нуль (8) вида z0 = eto (to g [0;п]). Тогда да i to . V^ tos n

• 1    - e + ^ a_se = 0 .

s = 1

Таким образом, существует to g [0;п], такое, что да

• 1    - cos to + ^ a_s cos s to = 0,

s = 1

да

• - sin to + ^ a_s sin s to = 0.

s = 1

Из (10) очевидно, что to ^ 0 .

Пусть m g R определено согласно Лемме 1.

__                        sin m to              .            - cos m to

Умножим (10) на                   , а (11) – на

~ . to (         1 )                        _ . to (        1 )

2sin —cos m — to          2sin —cos m — to

2 I 2 J                     2     (     2 J

Сложив полученные равенства, получим

----------7-----г— ( sin m to - . . to     (       1 )   ⁽

2sin — cos m — to

2     I      2 J

да cos to sin mto + sin to cos m to) + ^ as s=1

sin m to cos s to - cos m to sin s to

^2sin-^cos I ^{m -}-J^to

----------7-----7— ( sin m to - _o . to   (    1 v

2sin cos m — to

2     I      2 J

да sin (1 - m )to) + ^ as s=1

sin (m - s )to t • to     (      1)

2sin—cos m — to

2     I     2 J

= 0.

И окончательно да

1 + £ as s=1

sin ( m - s ) to

O • to     (       1 )

2sin —cos m — to

2     I      2 J

= 0.

Из (12) и (9) при неотрицательных значениях a_s  ( s = 1,2,...) получаем

” as л         П

⁵ = 1 2sin---------

2(2 5 - 1)

га

- 1 = л a_s

sin (m - 5) го

• п         го ■ to (       1)

2sni  „---. 2sin — cos m — го

2(2 5 - 1)       2     (     2 )

Это противоречит второму условию теоремы.

• 2.    Рассмотрим случай \ z 0I <  1. Рассмотрим окрестность точки z ₀, расположенную целиком внутри единичного круга | z | = 1, и такую, что на ее границе у нет нулей функции g ( z ).

га

По 1 условию теоремы ряд Л а₅ сходится. Отсюда следует, что последовательность много- 5 = 1 членов

k

Pk (z) = 1 - z + Лa5z5

5 = 1 сходится равномерно к функции g ( z ) внутри единичного круга.

Согласно теореме Гурвица [3] существует натуральное число k ₀ = к₀( у ), такое, что для любого натурального числа к >  к ₀ число нулей многочлена P k ( z ) внутри кривой у равно числу нулей функции g ( z ) внутри этой кривой. Значит, существует нуль многочлена P_k ( z ), расположенный внутри единичного круга.

С другой стороны, из второго условия теоремы получаем, что при любом к е N выполняется условие (3). Тогда, согласно теореме 1, уравнение (2) асимптотически устойчиво при любом значении к е N . Отсюда следует, что все корни соответствующего характеристического уравнения k

Лк - Лк-1 +ЛаХ-5 = 0

• 5 = 1

расположены внутри единичного круга. Следовательно, все нули многочлена P_k ( z ) расположены вне единичного круга при любом значении к е N . Получили противоречие.

Таким образом, все нули z ₀ функции g ( z ) расположены вне единичного круга. Согласно теореме 3 уравнение (1) асимптотически устойчиво. Теорема доказана.

Из леммы 2 и теоремы 4 получаем следующий результат.

Теорема 5 . Пусть выполняются условия:

• 1)    существуют действительные числа M >  0 и q е ( 0;1 ) такие, что для всех n е N выполняется а_п <  Mqⁿ;

га

• 2)    0 < Л 5а. < т . 5 = 1         ²

Тогда нулевое решение уравнения (1) асимптотически устойчиво.

Теоремы 4 и 5 являются бесконечномерными аналогами теорем 1 и 2 соответственно.