Прямое численное моделирование однородной изотропной магнитогидродинамической турбулентности с перекрёстной спиральностью

При численном моделировании МГД турбулентности с ненулевой перекрёстной спиральностью становится важным вопрос о методике введения энергии и спиральностей в систему. В работе [10] проведено сравнение разных способов возбуждения течения. Продемонстрированы недостатки детерминированных сил, способных привести к неконтролируемому внесению перекрёстной спиральности. Контролируемый приток энергии в систему обеспечивает случайная сила, которая не вводит в среднем никакие спиральности в течение. Метод воздействия на течение случайной силой был предложен в [11]. В последующие годы этот подход в различных модификациях применялся неоднократно как в чистой гидродинамике, так и в МГД турбулентности. [12, 13].

В работах [14–16] продемонстрированы преимущества пакета численного моделирования TARANG. Высокая гибкость программного кода, возможность получать информацию о спектральных свойствах течения непосредственно во время расчёта и решение уравнений в пространстве Фурье представляются выгодными при рассмотрении несжимаемой МГД турбулентности.

Цель данной работы — на основе прямого численного моделирования исследовать однородную изотропную МГД турбулентность, возбуждаемую случайным крупномасштабным источником энергии и перекрёстной спиральности, существующую в отсутствие внешнего постоянного магнитного поля. Для этого необходимо теоретически сформулировать силу, способную вносить перекрёстную спиральность постоянного знака. Реализация силы, расчёты и обработка результатов произведены автором в пакете TARANG.

• 2.    Математическая постановка

Эволюция несжимаемой МГД среды, находящейся под действием внешних сил, описывается уравнениями:

ат j

--= -U-VU + B-VB-VP + vV2U + F ,                       (1) dt

— = -U-VB + B-VU + nV2B + F,(2)

dt

V-U = 0,(3)

• V- B = 0.(4)

Здесь: t — время; U — скорость; B — нормализованное магнитное поле (b/^ ц ₀ цр ₀ , где ц ₀ и ц — магнитная постоянная и магнитная проницаемость, р ₀ — средняя плотность потока); P — полное давление, состоящее из нормализованного ( p /р₀ ) и магнитного ( B ²/2); V — оператор набла; F . и F ° — внешние силы; v и п = ( ^Ц ₀ ц ) ¹ — кинематическая и магнитная вязкости, где ст — электрическая проводимость.

В фурье-пространстве уравнения (1)–(4) принимают следующую форму:

^Uak) = - i Е[( U (q)-k) U (k - q))-(B (q)-k)B (k - q)]-iP (k) k-vk2 U (k) + F (k),(5)

d tq

^BTk) = -iZ[(U(q)-k)B(k-q)-(B(q)-k)U(k-q)]-nk2B(k) + F° (k),(6)

d tq k - U (k ) = 0,(7)

k - B (k ) = 0.(8)

Здесь: k и q — волновые векторы; все фурье-коэффициенты (величины, зависящие от волновых векторов) для краткости записаны с неявной зависимостью от времени; E_u и E_b — кинетическая и магнитная энергии, которые определяются по формулам

Eu (k) = Re [U (k) ■ U* (k)]/2,     Eb (k) = Re [B (k) ■ B* (k)]/2, а перекрёстная спиральность как

Hc (k) = Re[U(k)■ B* (k)]/2.

При исследовании МГД турбулентности полезными оказываются переменные Эльзассера, особенно, когда речь идет о течениях с высокими значениями перекрёстной спиральности. Именно в них в работах [6, 7] изучалась эволюция МГД турбулентности. Переменные Эльзассера находятся как z ± ( k ) = U ( k ) ± B ( k ) . Их поведение во времени, исходя из определения и уравнений (5)–(8), представляется следующим образом:

• -—— = - i^ [( z ± ( q ) ■ k)z ± ( k - q ) ]- iP ( k ) k - r ± k ² z ± ( k ) - r ^T k ² z ' ( k ) + F ± ( k ) ,           (9)

• 3.    Параметризация внешних сил

dt k ■ z ± = 0, где r± =(v±n)/2. Энергия в терминах z± имеет вид: E±(k) = Re[z±(k)■(z±) (k)]/2. Её также можно вычислить как E± (k) = Eu (k) + Eb (k) ± 2Hc (k).

Запишем случайную силу в виде:

Fu (k) = aeu (k ) + Yec (k) ,

F (k) = peь (k) + 5ec (k).

• k ^x e j

Здесь: el (k) = ।----— единичный вектор, перпендикулярный волновому вектору k , а e. — случайный Ik x e;| единичный вектор, уникальный для каждого вектора с индексом l, при этом l е{u, b, c}, и обновляющийся всякий раз при инициализации силы; а, р, у и 5 — неопределённые размерные параметры; сила действует в диапазоне масштабов волновых векторов, который, согласно условиям численного эксперимента, составляет: k'F < |k| < к1, где kOF и kF задают границы этого диапазона.

Мощности источников энергии и перекрёстной спиральности в данном случае можно представить в виде:

е E = 2 ^A t ( a ² +Y 2 ) N m , е E = 2 A t ( Р ² +5 ² ) N m , е ^C = A t y5 N m ,

где N m — количество мод, в которых действует сила, е E и е E — мощности источников энергии в полях U и B , е ^C — мощность источников перекрёстной спиральности H c .

Важно отметить, что е ^C , в отличие от мощностей е ^E , может быть меньше нуля, что соответствует внесению отрицательной H c . Этот эффект достигается за счёт того, что один из коэффициентов ( у или 5 ) фиксируется со знаком минус.

Определим три управляющих параметра:

R R ^е = ^е u ^+е b ,

C = —,

е

EE л 2 _ Sy еb

Л =        .

^е 5 ^е u

Здесь: б — суммарная мощность источников энергии; C — уровень подкачки относительной перекрёстной спиральности; X — весовой коэффициент, перераспределяющий вносимую каждым из 4 слагаемых силы энергию таким образом, чтобы при вариации значений у и 5 величины б E , б E и б C оставались неизменными. При этом б Е = A t у ² N m /2 и б ^е = А 1 5 ² N m /2 представляют собой мощности источников энергии в зависимости от параметров у и 5 . Они связаны с б C соотношением: ( б C ) = 4 б Е б ^Е .

Перепишем формулы (10), (11) в терминах управляющих параметров:

F (k) = (б(1 - CX)/2)12 eu (k) + (бCX/2) eс (k), F (k) = (б(1 -C(X)-1)/2)12 eь (k) + (бC(X)-1/^ ec (k).

Мощности источников (12)–(14) выражаются через управляющие параметры по формулам:

б E = s/ 2,     б E = б/ 2,     б c = б C .

Предложенная параметризация привела к взаимным ограничениям управляющих параметров, связанным с тем, что, согласно (12), (13) б E >  0 и б E >  0 :

C C ^{- 1}.                                        (16)

Отсюда следует, что при редельных значениях X в одном из полей источником энергии является только слагаемое, вносящее перекрёстную спиральность.

• 4.    Обработка результатов (постпроцессинг)

Численное моделирование уравнений (5)–(8) поставленной задачи является первостепенным. Но без последующей обработки результатов вычислительный эксперимент может оказаться бесполезным. Надёжное определение значений характеристик требует не только некоторого количества реализаций, но и достаточно длительного времени вычислений. Детальное моделирование расчётной области приводит к непомерно большим массивам чисел, сохранение которых в полном объёме становится невозможным. В связи с этим алгоритм исследования и процедуры обработки данных необходимо выбирать заблаговременно.

Классическим подходом при изучении свойств турбулентности служит построение графиков спектральных плотностей. На их основе оценивается развитость течения и ищется участок, близкий к закону «–5/3». Наличие участка является необходимым, но не достаточным признаком существования в спектре инерционного интервала, в котором энергия от масштаба к масштабу передаётся без потерь. Возникновение того или иного вида распределения спектральной плотности может быть вызвано различными механизмами турбулентного переноса энергии и спиральности. Однако только изучение взаимосвязанных спектральных потоков энергии и спиральности позволяет показать и однозначно интерпретировать полученные распределения спектральных плотностей и значения интегральных характеристик.

При подсчёте спектральной плотности существует проблема численного интегрирования функции по поверхности сферы на сетке в декартовом пространстве. Для удобства фурье-пространство волновых векторов разбивается на n сферических оболочек S n толщиной А к :

Sn = {k е Z3; n А к < |k| < (n +1) А к} .

Спектральная плотность энергии E_n рассчитывается по формуле, предложенной в [17]:

E. = тП Х E ( k ) l^k Г-

Mn kesn где Mn — число мод, принадлежащих Sn . Суммирование энергии мод с их относительными весами даёт возможность получить более точный результат, избегая сильных биений в длинноволновой части спектра [17]. Волновое число, ассоциированое с Sn , вычисляется как среднее:

k = — EW. n

M n k e S n

Спектральные потоки устанавливаются на основе спектральных функций переноса T_b^a ( k | p | q ) из моды a ( p ) в моду b ( k ) с помощью моды c ( q ), выступающей в роли посредника (здесь на месте фурье образов a , b и c может оказаться любая из мод U , B или z ± ). При этом волновые векторы k , p и q составляют триаду k + p + q = 0 .

В рамках данной работы рассмотрены следующие функции переноса:

T ( k | p | q ) = - Im { [ U ( q ) ■ k ] [ U ( p ) ■ U ( k ) ] } , T b ( k | p | q ) = Im { [ B ( q ) ■ k ][ B ( p ) ■ U ( k ) ] } , T ( k | p | q ) = - Im { [ U ( q ) ■ k ] [ B ( p ) ■ B ( k ) ] } , T ( k | p | q ) = Im { [ B ( q ) ■ k ][ U ( p ) ■ B ( k ) ] } , T Z ^{( k} | p | q ) = ^- Im { [ z ' ⁽ q ) ■ ^k ] [ z ± ⁽ p ) ■ z ±^{( k} ) ] } .

Рассчитывались спектральные потоки двух видов:

n ; < ( k 0 ) = S S T X ( k | p | q ),     П ~ ( k 0 ) = £ X T y ( k | p | q ).

Ip |< k 0 Iki < k 0                                                           pl < k 0 Iki ^: k 0

k + p + q =0                                          k + p + q =0

Здесь: x — источник; y — приёмник; вторые символы в верхнем и нижнем индексах (< или >) определяют направление суммирования; П у < ( k ₀) — поток, суммарно переданный из всех мод поля x с условием |p| <  k ₀ во все моды поля у с условием |k| <  k ₀ . Описание методики подсчёта потоков в коде TARANG приведено в работах [15, 16].

Заметим, что потоки в переменных Эльзассера ( П z ± > ) обладают полезным свойством: их сумма равна удвоенному полному потоку энергии П E , а их разность даёт удвоенный полный поток перекрёстной спиральности П C .

• 5.    Результаты расчётов

  Расчётная область представляла собой куб со стороной 2 п и периодическими граничными условиями. Сила действовала в диапазоне 1 <  k <  3. Во всех численных экспериментах фиксировался только управляющий параметр б , который составлял б = 2 . Приводимые далее результаты получены на сетке с 512³ узлами, так как данное разрешение позволяло достигать приемлемой детализации расчётной области за разумное время. Вычисления проводились с вязкостью v = 0,003 и магнитным числом Прандтля Pr _m = v/n = 1, которые соответствуют гидродинамическому и магнитному числам Рейнольдса R = Rm = 2094. Для достижения стационарного состояния требовалось около 30 единиц времени. После этого по следующим 10 единицам времени осуществлялись осреднения всех спектральных характеристик. От реализации к реализации варьировались величины C и X . Для проверки эффективности предложенного представления силы в численных экспериментах на основе компонент силы с различными значениями размерных параметров а , в , у и 5 находились фактические мощности источников энергии и перекрёстной спиральности. Значения управляющих параметров на входе в пакет TARANG и их фактические оценки ( б n , C_n и X n соответственно) представлены в Таблице.

• 5.1.    Интегральные характеристики

Параметр X управляет внесением энергий каждым из слагаемых силы (см. (15)). При C = 0 приток перекрёстной спиральности от соответствующих слагаемых отсутствует, поэтому фактическое значение X n становится неопределённым. Несмотря на статистическую оценку: ( U ■ e i ) = ( B ■ e j ) = 0, при большом, но не достаточном времени осреднения вклад оказывается не равным нулю. Поэтому в ходе моделирования учитывалось влияние и этих слагаемых. Упомянутый факт нашёл свое отражение в фактических — рассчитанных — значениях управляющих параметров, а также в интегральных и спектральных характеристиках.

Таблица. Сводный список всех реализаций в численных экспериментах, проделанных в данной работе

Обозначение численной реализии	Группа	Управляющие параметры на входе		Мощности источников			Вычисленные з управляющих па		начения раметров
		C	λ	ε uE	E ε b	ε C	ε n	Cn	λ n
A0	A	0	1	1,0	1,0	0	1,99	0,01	–
B1	B	0,1	1	1,0	1,0	0,2	2,00	0,10	1,05
B2		0,3	1	1,0	1,0	0,6	1,97	0,30	0,97
B3		0,5	1	1,0	1,0	1,0	2,08	0,52	0,99
B4		0,6	1	1,0	1,0	1,2	2,02	0,60	0,99
C1	C	0,5	0,5	1,0	1,0	1,0	2,01	0,51	0,50
C2		0,5	2	1,0	1,0	1,0	2,07	0,52	1,95

Численные эксперименты разбиты на три группы. Группа A состоит из одной реализации: рассматривается однородное изотропное турбулентное течение без внесения в среднем какой-либо спиральности. Конечное состояние этого течения является начальным условием для всех остальных реализаций из групп B и C. Сравнение полученных данных проводилось с двух позиций: во-первых, сопоставлялись характеристики групп B и A для определения степени влияния управляющего параметра C на распределение энергий по масштабам и на спектральные потоки; во-вторых, оценивалось влияние параметра λ на распределения при C = 0,5 по результатам реализаций из группы C и одному расчёту из B, а именно B3.

На рисунке 1 представлены интегральные характеристики течения из численных экспериментов с разными уровнями внесения перекрёстной спиральности. Несмотря на равномерное введение энергии как в поле U , так и в поле B уровень E_b заметно выше уровня E_u . Это приводит к тому, что выше и D_b , причём для всех запусков, которое держится на уровне ≈ 1,15 . Отсюда можно сделать вывод, что поле U

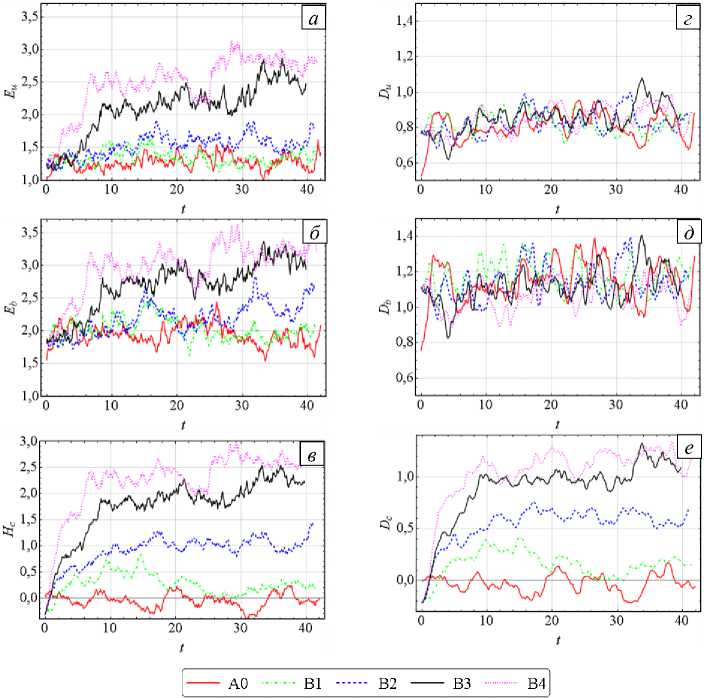
Рис. 1. Временная эволюция кинетической ( а ), магнитной ( б ) энергий и перекрёстной спиральности ( в ); скорости их диссипации ( г , д , е )

отдает полю B часть энергии, которая диссипирует уже там. Аналогичная ситуация наблюдается не только при внесении H_c . В работе [18] численно исследовалась спиральная турбулентность с источником энергии лишь в поле U . Установлено, что при определённых режимах E_b становится больше E_u . В работе [19] с помощью каскадных моделей изучалась неспиральная МГД турбулентность при малых Pr _m с источником энергии в поле U . Здесь также имеют место ситуации, когда E_b превышает E_u .

Уровень энергий E_u и E_b в течении возрастает с увеличением уровня H_c . Учитывая, что скорости диссипации энергий одинаковы для всех реализаций, возрастание нельзя связать с бо_́льшим внесением энергии. Рост H_c приводит к накоплению энергии в крупных масштабах (см. [8, 9]). Этот эффект также проиллюстрирован ниже на распределениях спектральных плотностей энергий (см. Рис. 2).

• 5.2.    Спектральные плотности

На рисунке 2 показаны компенсированные спектральные плотности энергий и относительной перекрёстной спиральности для нескольких реализаций. Данные распределения демонстрируют в первую очередь то, что в отсутствие постоянного источника перекрёстной спиральности (реализация A0) короткий участок спектра становится почти горизонтальным. Это говорит о зарождении инерционного интервала. К сожалению, использованное разрешение не позволяет рассчитывать, что он будет выраженным [16]. При существенной подкачке перекрёстной спиральности наклон кривых меняется (см. реализации группы B).

Наглядно проиллюстрировать изменение наклона удаётся с помощью компенсированных спектральных плотностей энергий в переменных Эльзассера (Рис. 3). Видно, что с ростом H_c увеличивается наклон только кривых E ⁺ , в то время как кривые E - становятся более пологими, что свидетельствует о различиях в скорости обмена энергией между волновыми масштабами k в зависимости от сонаправлености полей в них.

ЕЛЮк513

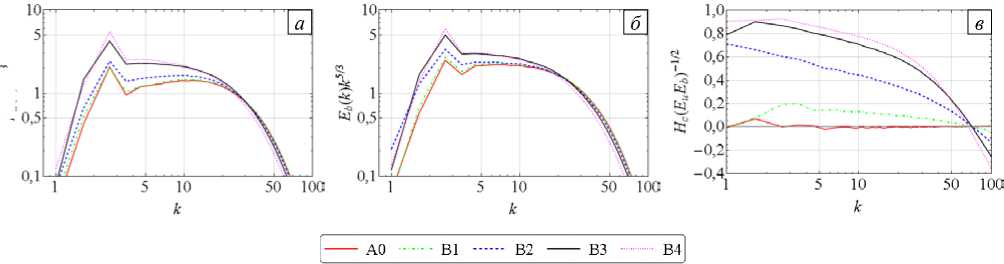
Рис. 2. Компенсированные спектральные плотности кинетической ( а ) и магнитной ( б ) энергий и спектральная плотность относительной перекрёстной спиральности ( в )

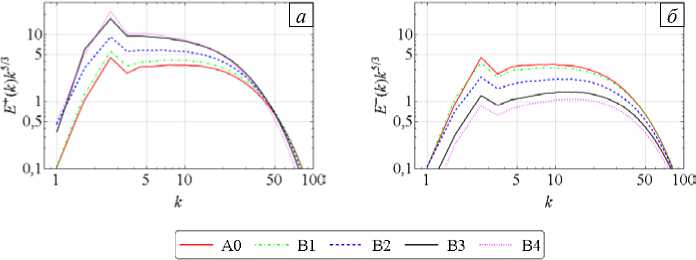
Рис. 3. Компенсированные спектральные плотности энергий в терминах переменных Эльзассера: E ⁺ ( а ) и E ( б )

• 5.3.    Спектральные потоки

Рисунок 4 содержит кривые осредненных спектральных потоков энергий и перекрёстной спиральности. Поток полной энергии является суммой, состоящей из энергий, переходящих от мод с модулем волнового вектора, меньшим k ₀ , в моды с модулем волнового вектора, длина которого больше k ₀ :

E U <  U <      B <      B <

^{П П} U >  ^{+ П} B >  ^{+ П} B >  ^{+ П} U >  .

При рассмотрении П E (Рис. 4 а ) для разных реализаций видно, что при повышении уровня H c полный поток энергии, несмотря на неизменный уровень внесения энергии, несколько снижается и свидетельствует, что роль диссипации в крупных масштабах становится значительнее. Величина потока П C (Рис. 4 б) возрастает, и одновременно с этим увеличивается угол наклона кривых потока на масштабах |k| >  5, что согласуется с поведением спектральных плотностей относительной спиральности (см. Рис. 2 в ), которые демонстрируют, что вне зависимости от уровня внесения перекрёстной спиральности масштаб диссипации остаётся прежним. Это и приводит к увеличению наклона кривых потока П ^C с ростом их максимального уровня. Потоки в переменных Эльзассера (Рис. 4 в , г ) представлены в сокращенных обозначениях: П ⁺ = П z ₊> , П ^- = П z - > . Величина потока П ⁺ повышается, при этом, как и у спектральных плотностей (Рис. 3 а ), наклон кривых растёт. Графики же П - ведут себя наоборот: приближаются к горизонтальному положению и образуют участок, близкий к инерционному интервалу.

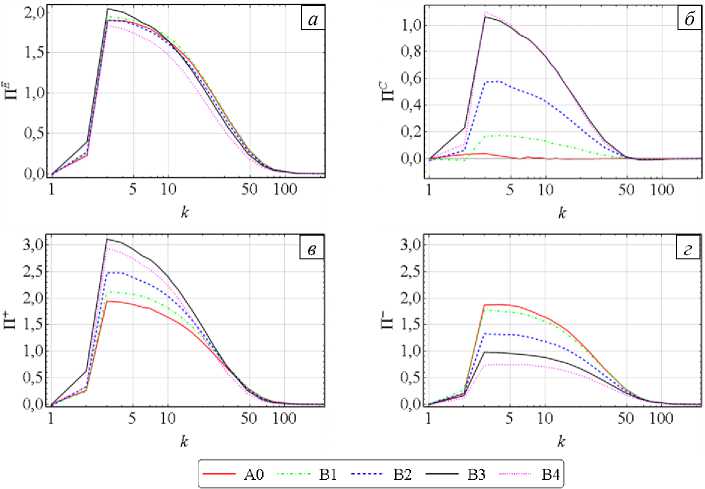
Рис. 4. Спектральные потоки: полный поток энергии ПE (а), поток перекрёстной спиральности ПC (б); потоки энергии в переменных Эльзассера - П+ (в) и П (г)

На рисунке 5 представлены спектральные потоки энергии по отдельности для каждого из полей:

п E = п ^и <  + п ^и <  + п ^и <  u U >  ⁺ B > ⁺ B <  ,

E     B <      B <      U <

^П ь   ^П B > ^{+ П} и >  ^П B <  .

Поток Π _u ^E выражает, какое количество энергии передаётся от меньших по длине волного вектора мод U в остальные моды поля U и во все моды поля B . Кривые Π _u ^E показывают, что поле U отдаёт часть энергии полю B (кривые потока выше нулевого уровня при высоких значениях модуля волнового вектора:

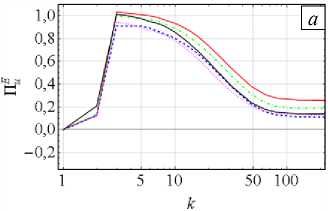
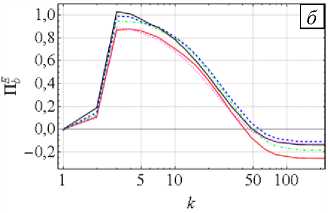
АО В1 ...... В2 --- ВЗ ............. В4'

Рис. 5. Потоки энергии для поля U ( а ) и поля B ( б )

|k| >  100. Поток П E демонстрирует, что B получает часть энергии от U . С возрастанием параметра C уменьшается количество энергии, поступающее в меньшие масштабы при тех же |k| >  100. Этим косвено подтвержается усиление диссипации в крупных масштабах из-за более высоких значений энергии в них.

• 5.4.    Несбалансированное внесение перекрёстной спиральности

• 5.5.    Сравнение результатов

Варьирование величины управляющего параметра X дало неожиданные результаты. Рассматривались случаи (см. Таблицу) с высоким уровнем внесения перекрёстной спиральности (реализация B3, C = 0,5) и предельно возможными для этого уровня значениями X (реализации C1 и C2, соответственно Х = 0,5 и Х = 2, см. (16)). В реализации С1 энергия в поле B вводилась только слагаемым, ответственным за перекрёстную спиральность ( р = 0); в С2 имела место аналогия для поля U ( а = 0) (см. выражения для сил (10), (11)). За счёт такого перераспределения вкладов каждой из компонент силы течению сообщалось одинаковое количество энергий и перекрёстной спиральности. Различие состояло только в том, что разными были уровни мощности источников перекрёстной спиральности в полях U и B . Однако, несмотря на это, интегральные и спектральные характеристики показали качественное и количественное согласие.

На рисунке 6 представлены сводные графики спектральных плотностей для трёх течений с одинаковым уровнем вводимой перекрёстной спиральности, но с разным балансом компонент силы. Лишь для реализации С1 на самом крупном масштабе (| Х | = 1) обнаруживаются несущественные отклонения кривых друг от друга.

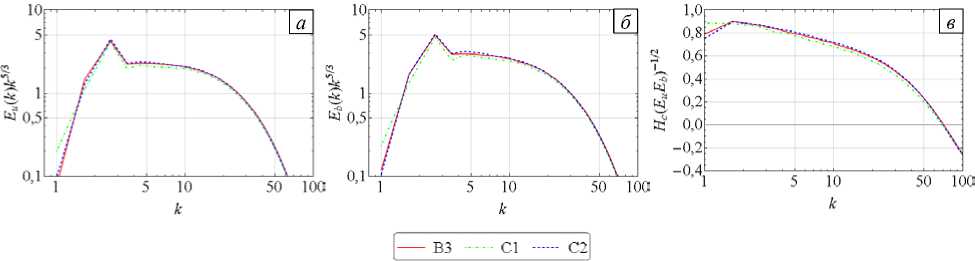
Рис. 6. Компенсированные спектральные плотности: кинетическая ( а ) и магнитная ( б ) энергии; относительная перекрёстная спиральность ( в )

В работах [8, 9] с помощью каскадных моделей подробно рассмотрено влияние перекрёстной спиральности на спектральный перенос и накопление энергии. Текущий подраздел посвящён качественному сравнению найденных в рамках данного исследования зависимостей с опубликованными в [8, 9]. На рисунке 7а показано распределение осреднённой по времени полной энергии EE') = EEU + Eb') как функции управляющего параметра C . Осреднение обозначено угловыми скобками .... В качестве асимптотической кривой (см. на рисунке пунктирную линию) взята гиперболическая зависимость f (C) = a + b(1 - C)-3, где a и b — константы, выбранные из условия наименьшего отклонения f от экспериментальных значений ^E^ (C), изображённых на рисунке точками. Видно, что результаты численных экспериментов также близки к гиперболической зависимости, как показано в [8, 9]. При доступных автору в настоящее время вычислительных ресурсах получение аналогичных количественных оценок не представляется возможным из-за нереализуемо больших чисел Рейнольдса, использованных в каскадных моделях. Энергия не достигает столь же высоких значений в связи с диссипацией, начинающей действовать в крупных масштабах, в то время как в каскадных моделях диссипация проявляется при бо́льших значениях энергии. В бездиссипативном приближении при максимально возможной перекрёстной спиральности энергия будет расти бесконечно, что соответствует гиперболической зависимости, приведённой на графике.

На рисунке 7 б приведена зависимость средней относительной перекрёстной спиральности (HC^ = ( Hc V( E) от параметра C . Здесь результаты количественно ближе к данным из [8].

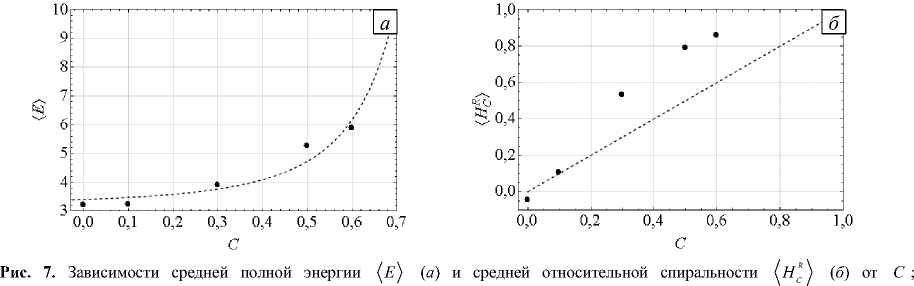
пунктирная линия на ( б ) взята из работы [8] для сравнения

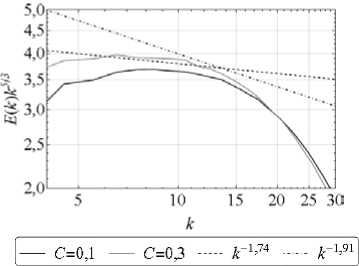
Рис. 8. Компенсированные спектральные плотности полной энергии E ( k ) для различных значений C : прямые штриховые линии с наклонами –1,74 и –1,91 [9] приведены для справки

Количественное отличие становится меньше за счёт того, что рассматриваются относительные величины, на которые диссипация действует в равной степени. Это сводит её влияние к минимуму.

На рисунке 8 построены кривые компенсированных спектральных плотностей полной энергии E ( k ). Прямые с наклонами к ^{- 1,1} 4 и к ^{- 1,91}, взятые из [9], приведены для справки. Если при C = 0,1 наблюдается некоторое согласие короткого участка с соответствующей прямой, то для C = 0,3 о каком-либо совпадении говорить не приходится, как и о наличии на кривых инерционных интервалов. Предполагается, что это, в первую очередь, связано с отсутствием у спектральных потоков, построенных по экспериментальным данным (Рис. 4), горизонтального участка.

• 6.    Заключение

В работе рассмотрен способ возбуждения несжимаемой МГД турбулентности с перекрёстной спиральностью. Случайная сила способна обеспечить постоянный приток энергии с контролируемым уровнем перекрёстной спиральности. Описанный подход реализован в рамках программного пакета TARANG путём создания дополнительных библиотек. Проведена серия расчётов, демонстрирующих эффективность предлагаемого представления силы и отклики, возникающие на её действие.

Получены однородные изотропные турбулентные распределения с различными уровнями перекрёстной спиральности без приложения внешнего постоянного магнитного поля. Во всех случаях спектральный перенос энергии показал, что поток энергии из поля скорости в поле магнитной индукции положителен. Скорости диссипации энергии в полях скорости и магнитной индукции также подтверждают этот факт. В среднем отношение скоростей диссипации магнитной энергии к кинетической составляет ® 1,3 . Данный эффект не является уникальным. Даже в случаях, когда источник энергии влияет только на поле скорости, возможны ситуации, когда уровень энергии магнитного поля выше, чем у поля скорости. Это обнаружено, например, как при численном моделировании в [18], так и с помощью каскадных моделей в [19].

Спектральные характеристики в переменных Эльзассера z ± выявляют существенное различие в наклонах спектральных плотностей и потоков при высоких уровнях перекрёстной спиральности. Максимальные значения спектральной плотности E ⁺ и потока П⁺ возрастают, и наклон соответствующих кривых с повышением внесения относительной перекрёстной спиральности увеличивается, в то время как характеристики поля z ^- количественно падают, их наклон уменьшается, и наблюдается формирование короткого участка инерционного интервала (горизонтальной части кривой потока).

Детальное сравнение полученных результататов с вычисленными на основе каскадных моделей [8, 9] показало качественное согласие. Количественного совпадения достичь не удалось из-за нереализуемо больших чисел Рейнольдса, для которых проведены расчёты с помощью каскадных моделей. Внесение перекрёстной спиральности приводит к накоплениею энергии в крупных масштабах. Уровни относительной перекрёстной спиральности продемонстрировали хорошее количественное согласие с результатами из [8]. Наклоны участков спектральных плотностей энергии имеют некоторое, хоть и не явное в виду отсутствия выраженного инерционного интервала, подобие наклонам, приведённым в [9].

Данные численных экспериментов позволяют сделать вывод, что при использовании случайной силы не важно, в какой степени — равной, большей или меньшей — корректируются поле скорости и магнитное поле для достижения нужного уровня корреляции. Так, в численных экспериментах параметры γ и δ , характеризующие сонаправленное изменение полей U и B , соотносились, соответственно, как 1 к 4 и 4 к 1. На интегральные и спектральные характеристики течений это не оказало заметного влияния, но открыло большую свободу в возбуждении течения с необходимыми уровнем перекрёстной спиральности, в том числе и в случаях, когда в течении может действовать дополнительный источник другого типа, например, создающий искуственную диссипацию энергии.

Предложенный подход к формулировке силы может применяться как для исследования других способов возбуждения МГД-турбулентностей с ненулевой перекрёстной спиральностью, эволюционирующих в различных условиях, так и для получения однородных изотропных распределений с заданными свойствами при изучении процессов диссипации в них.

При проведении работ был использован вычислительный кластер «Тритон» (ИМСС УрО РАН, Пермь).