Прямой метод решения системы линейных алгебраических уравнений на основе вейвлет-разложения
Бесплатный доступ
Рассматривается прямой метод решения СЛАУ, в основе которого лежит нестандартное представление в вейвлет-базисе матрицы системы. Дается краткое введение в вейвлеты и описывается нестандартное представление оператора в вейвлет-базисе. Обсуждается, почему прямой метод при использовании вейвлетов становится эффективным, даже когда рассматриваются плотнозаполненные матрицы.
Короткий адрес: https://sciup.org/147158532
IDR: 147158532 | УДК: 519.612.2
Текст научной статьи Прямой метод решения системы линейных алгебраических уравнений на основе вейвлет-разложения
Существует много доступных методов решения больших сильноразреженных систем (СРС) линейных уравнений. Наиболее популярными методами решения для таких систем являются итерационные методы.
Прямые методы решения СРС могут также использоваться для решения таких систем. Их эффективность зависит от числа дополнительных ненулевых членов, полученных в ходе LU-факторизации матрицы системы. Напомним, что некоторые разреженные системы не имеют разреженных LU-факторов. В работе [2] предложен метод построения разреженного представления матриц, которые изначально плотно-заполнены.
Далее будет показано, что, если использовать нестандартное представление в вейвлет-базисе матрицы системы, соответствующие LU-факторы будут также сильноразреженными, это делает эффективным прямой метод решения СЛАУ.
Перечислим основные определения и свойства вейвлетов.
Вейвлет-функция у строится по масштабирующей функции ф, которая обладает двумя свойствами:
-
а) система функций ^ф^х-кук е Z\ ортогональна в L2^R^,
-
б) функция является решением функционального уравнения
Ф^х^^^^ф^х-ку(1)
к
Тогда для вейвлет-функции у/ верно представление
Ф^ = J2^-V)k Их_кф(2х-ку(2)
к
Наибольший интерес представляют компактно-сосредоточенные функции ф и ф . В этом случае фильтр hk конечен.
ф к (*)= 2/2 ф12^х-к]. Через Иу обозначим линейную оболочку $рап<2/2ф( 2' - к I, к е Z).
Из соотношения (1) следует, что
...с И , с:Иос^ с...
Определим подпространство И7 как ортогональное дополнение Е, в И7+1, т.е.
= j/ © л;. Если Ц?; = Т2 (Я) и Qc7 = {О}, то доказывается в [1], что j j
Система функций |^7 к (х)
у>0
и ур0 к (х)| является ортогональным базисом в пространстве
£2 (7?). В частности, У„ = Д, Ф0<у<и-1 ^ •
Тогда система функций ^7к (х)( . 0 и ^оТ Wj ’ где является ортогональным базисом в Т2(0,1). Определим проектор Р на подпространство Vpj^Z, и Q на подпространстве И7, где Q3 =Pj^-Pj . Для линейного оператора Т :£2(0,1) -> Т2(0,1) оператор Т} =PjTPj будет на зываться дискретизацией оператора Т масштаба j. В базисе ф1 4(х,у) с оператором Тй можно связать матрицу То размера 2V х 27.
Введем ортогональную матрицу
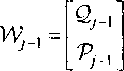
где РрХ и Q;_, - матричное представление проекторов Pj-X и QpX соответственно. Пусть ху = Т^х и уу = Р,у - дискретизации элементов х и у из L" (0,1). Для того, чтобы свести
ТЛ)=У:> к масштабуу-1, применим (3) и (4)
Получим
А-1 ^/-1
где d} =О,]У, Sj = P}y, dpX --Q^x, s x = P xx, в то время как Лу_], В^х и Cy_t - матричные операторы
сн-лрн-^_х
^-i -Q.J_\TQ,J_X Bj-x =Q-j-\TPj-\ Cj_x - T’ _jTQ7_1 T^^TP^
Матрицы Aj_x, B^x и C^ содержат уточняющую информацию об операторе Т]-х . На следующем шаге матрица Т;Л извлекается из (6), и к ней применяется ортогональная матрица
И^-2, как и в (5). Эта процедура продолжается на всех масштабах j = п -1,...,0. Результатом является нестандартная форма (NS-форма) исходной матрицы То. Для j0 =3 NS-форма матрицы 7g показана на рис. 1. Здесь дг$} и dpSj связаны соотношениями dj =Ajdj +BjSp
Филиппов О.В. Прямой метод решения системы линейных алгебраических уравнений
_______________________________________на основе вейвлет-разложения и на последнем шаге
»о = CqSq + Toso.
Для того, чтобы конвертировать < d^s, I в вейвлет-представление UdA , $n ,
' r r I 1 r (I ЛО<7<7ОД’ следует воспользоваться алгоритмом:
-
1. d. । =0, s , = 0.
-
2. d, = QJ (s^ + s^ ), s, = P( (s^ + sj4 \
-
3. Тогда d} = d] + d}, а на последнем шаге s0 = s0 + s0. Пусть система функций yk (?) ортогональна и
- где коэффициенты ck вычисляются по функции
Vo-1 ’
4 = VWkW1-
Если i//k (?) имеют нулевые моменты
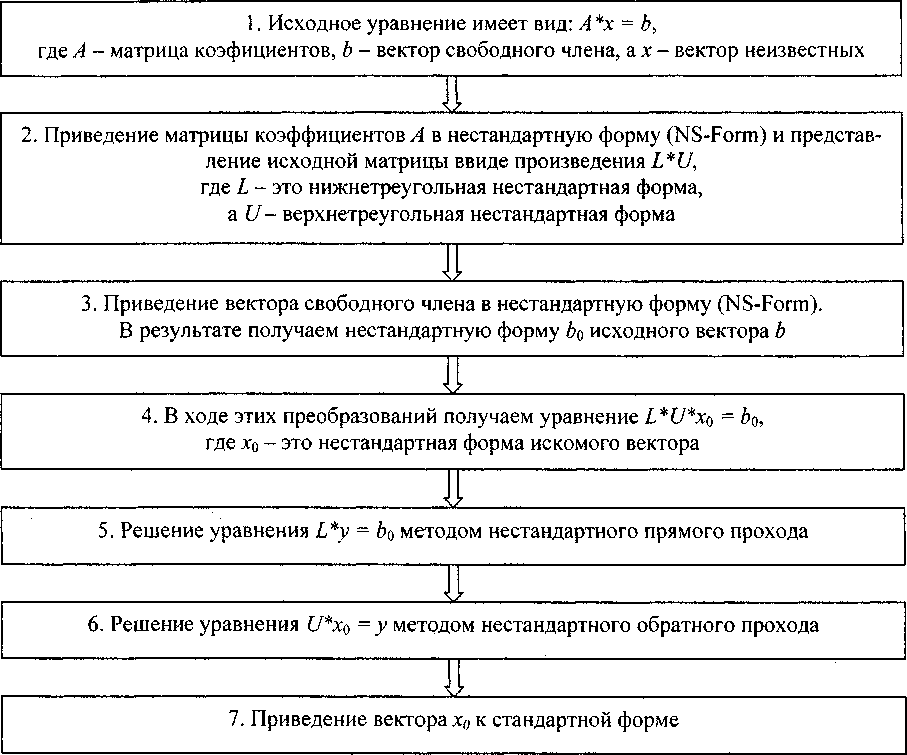
0 = У^к (f)dt,0 Если Т является интегральным оператором и его ядро - гладкая функция вне диагонали, то матрица, полученная «дискретизацией», имеет много малых элементов вне диагонали. Такие матрицы после «сжатия» имеют разреженное представление в вейвлет-базисе. Поэтому NS-форма матрицы после «сжатия» становится сильно разреженной. Алгоритм Рассмотрим алгоритм решения СЛУ методом нестандартного представления в вейвлет-базисе. Его общий вид можно увидеть на рис. 2. Рис. 2. Алгоритм Прокомментируем шаг 2. Выше уже описывался способ построения нестандартной формы матрицы, но для данного алгоритма предлагается совместить его с LU-разложением (более подробное описание данного подхода можно увидеть в работе [2]). Результирующая процедура получится более эффективной, чем если бы нестандартное и LU-разложения применялись независимо. В начале расчитаем вейвлет-разложение оператора Тп для «первого» масштаба: т„= Л-i + Л-i + Л-i + Л-i= где Л-1 =Л-ЛЛ-ц Л-1= Л-ЛЛ-ь Используя стандартное LU-разложение, получим: Л-1 = Л-1Л-ц и зададим Ап_х = Ln_x и Ап_х = Un_x. Имея Ап_х и Ап_х, можно получить Вп_х и С„_х решая Л-1Л-1= Л-1 ’ Л-1 Л-1= Л-1 с помощью стандартных методов прямого и обратного прохода. Филиппов О.В. Прямой метод решения системы линейных алгебраических уравнений на основе вейвлет-разложения Для продолжения на следующем масштабе необходимо вейвлет-разложение оператора Тп_х и СП_ХВП_Х. Эти процедуры могут быть скомбинированы, если вначале вычесть СП_ХВП_Х из Тп_х, а затем рассчитать 4-i ~4-i4-i =(4-2 -4-2)+(4-2 -4-2)+(4-2-4_2)+(г„_2-т^у (?) где 4-2 "4-2 = 4-2(4-! ~Cn_xBn_x^Qn_2, 4-2 "4-2 ”Qn-2^n-l "СпЛВп_^Рп_2, Cn-2 ~Cn_2 =Pn_2^T„_x -Cn_xBn_x^Qn_2, 4-2 - 4-2 = 4-2 (4-1 ~ Cn_xBn_x ^Pn_2. Используя стандартное LU-разложение, получим 4-2 ~ 4-2 = 4-г4-2’ где 4-2 =4-2 и 4-2 = 4-2 ' Имея 4-2 и 4-2» МОЖНО получить 4-2 и 4-2 Решая 4-24-2 = 4-2 " 4-2 ’ 4-г4-г = 4-2 "4-2» с помощью стандартных методов прямого и обратного прохода. Для продолжения необходимо рассчитать вейвлет-разложение Тп_2, СП_2ВП_2 и дополнительного члена Тп_2 из равенства (7). 4-2 _4-24-2 "4-2 =(4-з "4-з)+(4-з ~4-з)+(4-з "4-з)+(4-з ~4-з)» где 4-з" 4-з = 4-з (4-2" 4_24-2 ~ 4-2) 4-3» 4-з "4-з =4-з (4-2 ~4-24-2" 4-2) 4-3’ ■ 4-з - 4-з = 4-з (4-2" 4-24-2" 4-2) 4-з » 4-з" 4-з = 4-з (4-2" 4-24-2 - 4-2) 4-3- Процесс продолжается до масштаба п, где рассчитываются члены То и То . Программа На основе вышеприведенного алгоритма нами была разработана программа1 для решения СЛАУ. В качестве языка программирования был выбран Fortran90, для работы с сильно разреженными матрицами была использована библиотека SPARSKIT2. Основную работу выполняет процедура solveUsingNSForm, на вход которой подается матрица коэффициентов, вектор свободного члена, векторы коэффициентов материнской и вейвлет-функций, количество вейвлет-преобразований, которое необходимо будет проделать над матрицей коэффициентов в процессе получения нестандартной формы, и переменная, в которой будет возвращен вектор неизвестных. Стоит отметить, что все матрицы и векторы передаются в сжатом формате (так называемый, формат CSR). Работу процедуры solveUsingNSForm можно разделить на 5 частей. 1. Расчет нестандартного представления для матрицы коэффициентов. Это работу проделывает процедура createNSForm2Dim. Ей на вход подается матрица, которую необходимо преобразовать, векторы коэффициентов материнской и вейвлет-функций, количество преобразований и переменные, в которых будут возвращены верхнетреугольное 2. Расчет нестандартного представления для вектора свободного члена. Для этого используется процедура createNSFormlDim. Ей на вход подается вектор свободного члена, векторы коэффициентов материнской и вейвлет-функций, количество преобразований и переменная, в которой будет возвращен результат - нестандартная форма вектора. В процессе выполнения данной процедуры исходный вектор претерпевает заданное количество вейвлет-преобразований, причем получающиеся векторы запоминаются в переменную-результат. 3. Решение первого уравнения (см. шаг 5 алгоритма) в нестандартной форме методом прямого прохода. Для этого используется процедура nsForwardSubstitution. На вход подается нижнетреугольная нестандартная форма, вектор свободного члена в нестандартном представлении, векторы коэффициентов материнской и вейвлет-функций и переменная, в которой вернется результат решения. 4. Решение второго уравнения (см. шаг б алгоритма) в нестандартной форме методом обратного прохода. Эту работу выполняет процедура nsBackwardSubstitution. На вход подается верхнетреугольная нестандартная форма, результат, полученный на предыдущем шаге, векторы коэффициентов материнской и вейвлет-функций, переменная, в которой вернется результат решения. 5. Обратное вейвлет-преобразование для получения вектора решения в стандартной форме. Для этого используется процедура inverseWaveletTranslDim, на вход которой подается вектор материнских и вейвлет-коэффициентов первого масштаба искомого вектора, векторы коэффициентов материнской и вейвлет-функций, переменная, в которой вернется результирующий вектор. и нижнетреугольное нестандартные представления исходной матрицы. Данная процедура выполняется, четко следуя шагу 2 вышеприведенного алгоритма. Для проведения всех стандартных действий над матрицами и векторами используются процедуры и функции из библиотеки SPARSKIT2. Она содержит процедуры для преобразования матриц из стандартного формата в «сжатый» и обратно, решения СЛАУ методами прямого и обратного прохода, LU-разложения матрицы, умножения и сложения матриц и так далее. Численные результаты В этом разделе представлены численные результаты обработки нескольких примеров для демонстрации быстродействия и точности алгоритма и программы. Для тестирования был выбран компьютер с процессором Intel(R) Pentium(R) 4 CPU 3,00GHz c 2048Mb оперативной памяти. Пример 1. Для первого примера была выбрана матрица вида: I 1, где N -Т - размерность матрицы, ij = 1..2" и С = \!1П ■ Правая часть матричного уравнения подбиралась так, чтобы существовало известное точно решение. Данная СЛАУ была решена при помощи нестандартного представления и при помощи библиотеки Lapack. Из этого пакета была выбрана процедура DSGESV, реализующая один из наиболее часто используемых итерационных алгоритмов решения СЛАУ. Более подробно об этом алгоритме можно узнать из документации, расположенной по адресу Результаты можно увидеть в табл. 1. Таблица 1 N TNS l4n4 ^(Ж) T Lapack Ь4^арас4 Ьг4аРасЦ 29 0,68 1,74-104 4,59-IO-4 0,78 3,11 • 1 O'15 l,3610~14 210 3,35 4,25-IO-4 1,19-Ю-3 6,18 3,33 10"15 2,48-10-14 2й 19,32 6,53 IO-4 2,25-10-3 48,18 9,05-10-15 8,39-Ю'14 В первом столбце этой таблицы находится размерность обрабатываемой матрицы, во втором время в секундах работы алгоритма на основе нестандартного представления, в третьем и четвер- Филиппов О. В. том ошибка данного алгоритма, в пятом время работы в секундах процедуры из библиотеки Lapack, в двух оставшихся - ошибка этой процедуры. Пример 2. Во втором примере использовалась матрица вида: [sin^--^), i*j . 1, i = j где N = 2" - размерность матрицы и i,j = \..2n. Правая часть данного матричного уравнения подбиралась так, чтобы существовало известное точно решение. Результаты можно увидеть в табл. 2, построенной аналогично табл. 1. Таблица 2 N ^NS L»(NS) l^ns) т zLapack L^Lapack^ L^ Дараск^ 29 0,73 1,46-104 1,0Ь10'3 0,78 5,81-Ю”13 3,73-Ю"12 210 1,83 1,58-Ю-3 3,54-10'2 6,15 1,54-Ж12 1,24-10^" 2" 8,14 1,47-10^ 2,8L10-2 48,59 4,17-Ю"12 4,9Ь10~п Здесь стоит отметить, что, хотя алгоритм на основе нестандартного представления работает и быстрее, чем процедура из библиотеки Lapack, но точность полученного решения у него существенно ниже. Снижение точности происходит вследствие трешолдинга, производимого в момент вейвлет-преобразования и LU-разложения. Суть трешолдинга состоит в том, что величины меньше некоего заданного порога считаются равными нулю. Все предыдущие примеры обрабатывались с порогом равным 10”5. В табл. 3 можно увидеть, как будет меняться точность и время решения, если уменьшать этот порог. Таблица 3 Порог TNS 1ДП8) 10~8 43,55 1,51-Ю-8 7,75-1О-8 10"9 44,38 1,29'10'9 2,13-Ю-9 10"” 48,01 6,78-10^12 7,84-Ю41 Таким образом, видно, что для порога равного Ю-11, ошибка решения становится одного порядка с ошибкой процедуры Lapack. Что касается времени выполнения, то оно также становится сравнимым. Однако, стоит взглянуть что произойдет на следующей размерности матрицы (табл. 4). Таблица 4 N TNS МЖ) ь2(ж) Т Lapack L^ (Lapack} Z2(Lapack} 212 362,87 1,ЗЫО"10 5,ОЬ1О~10 387,36 1,46-Ю*1’ 2,03'10~10 Время работы алгоритма на основе нестандартного представления сопоставимо и даже несколько меньше, чем время работы итерационного алгоритма при сравнимой ошибке. Стоит отметить, что для вейвлет-преобразований, подбирая вейвлет-функцию, можно добиться существенно-большего числа нулей в результате, а значит, увеличить общую скорость. Для данных примеров использовалась вейвлет-функция D4 (Добеши 4 порядка). Итак, можно сделать вывод о том, что алгоритм решения СЛАУ на основе нестандартного представления работает сравнимо по времени выполнения и по ошибке результата с итерационными алгоритмами.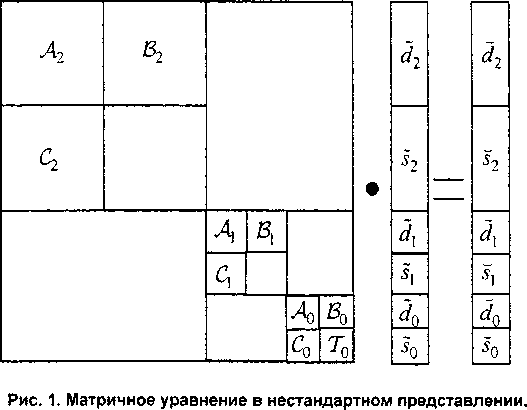
Список литературы Прямой метод решения системы линейных алгебраических уравнений на основе вейвлет-разложения
- Добеши, И. Десять лекций по вейвлетам/И. Добеши. -Ижевск: НИЦ «Регулярная и хаотическая динамика». -2001. -464 с.
- David L. Gines LU Factorization of Non-Standard Forms and Direct Multiresolution Solver/David L. Gines, G. Beylkin, J. Dunn. -Appl. Comput. Harmon. Anal. -1998. -№ 5(2). -P. 156-201.


