Прямоугольный волновод с активной полупроводниковой пленкой с поперечным дрейфом носителей заряда и намагниченными ферритовыми слоями

Прямоугольный волновод с активной полупроводниковой пленкой с поперечным дрейфом носителей заряда и намагниченными ферритовыми слоями

Рассмотрим H { Ey, H _x, H _z}

- волны в двумерной слоистой структуре

(

зависимость вдоль оси x отсутствует ) с полупроводниковой пленкой ( тонкий n-GaAs слой ) с отрицательной дифференциальной проводимостью, расположенной между ферримагнитными слоями , подмагниченными вдоль оси x (см. рис. 1 б). Ферримагнитные слои расположены между металлическими плоскостями с идеальной проводимостью. Такая структура является моделью прямоугольного волновода ( рис. 1 а ) для волн Н -типа.

Полупроводниковый слой в активных волноведущих структурах с поперечным дрейфом носителей заряда в реальных приборах имеет малую толщину. Дифференциальная проводимость полупроводника при приложении сильного статического электрического поля Е₀ вдоль оси x на рис. 1.1. б ( для n-GaAs, E 0 ~ 3.5 kB/см ) становится отрицательной и появляется возможность усиления электромагнитных волн. В общем случае проводимость активного слоя анизотропна, и статическое поле E₀ (поле смещения ) имеет неоднородное распределение по координате x, связанное образованием статических доменов в полупроводниковой пленке [1]. Однако в этом разделе эти физические особенности учитываться не будут.

При распространении электромагнитной волны вдоль оси z ( зависимость по координате z и времени t ex pirn t - iyz}; у = y* -iy"-комплексная постоянная распространения ) в полупроводниковом слое p возникает электрический ток с плотностью j . В линейном (малосигнальном) приближении в пренебрежении волнами пространственного заряда и анизотропии проводимости проводника в полупроводниковом слое возникает ток с плотностью j = о E, где о - дифференциальная проводимость полупроводника.

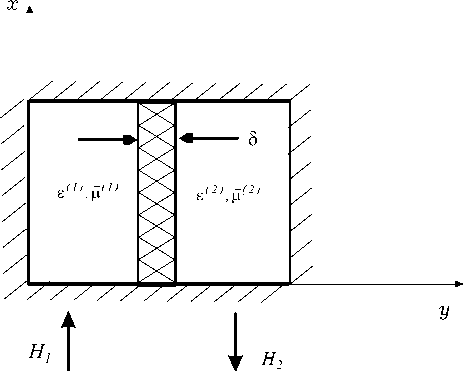
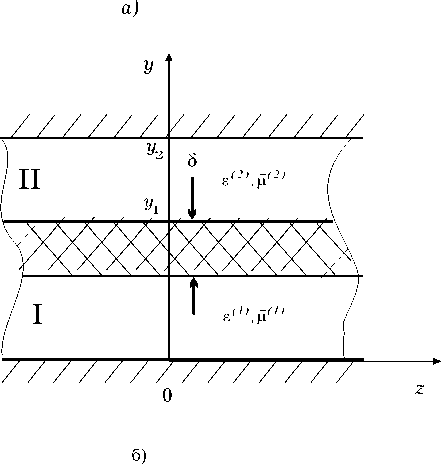
Рис.1. Активные линии передачи с полупроводниковыми плёнками и ферритовыми слоями: а- поперечное сечение прямоугольного волновода;

б- плоская активная структура

Влияние тонкого полупроводникового слоя на распространение электромагнитных волн в структуре учтем введением на поверхности y = y i ( см. рис. 1 б ) линейного электрического тока

J _T = 5 а E _T ,                   (1)

где нижний индекс т означает касательные составляющие к плоскости у = у .| соответствующих векторов.

Таким образом, получаем следующую модель расчета волноведущей линии передачи с активной полупроводниковой пленкой ( рис. 1 б ): линия передачи с намагниченными ферритовыми слоями и линейным электрическим током (1) на границе у = у₁.

Так как электрический ток (1) на границе у = у -j не изменяет граничных условий для тангенциального электрического поля на этой границе, то для Н - волн можно записать следующие граничные условия при У = У i :

Ex' ) = Ex ² ) , Hz' ) - Hz ² ) = 4 ; а 5 EX ) ,           (2)

где с- скорость света.

Намагниченные ферритовые слои I и II ( см. рис. 1) характеризуются тензорами магнитной проницаемости   ц(n) (n = 1,2) ( оси гиротропии направлены вдоль оси x ):

	' 1     0	0   '
Ттn >  =	0   цn 1	- i Цаn )	,                         (3)
	10 in'an )	А( n 1 J

( n )      ( n )

где Ц ) , ца, - соответственно диагональные и недиагональные элементы

^Т ( n )

тензора ц ⁷

В предположении отсутствия вариации поля вдоль оси x , для волн, распространяющихся вдоль оси z в структуре, изображенной на рис. 1 б, нетрудно получить следующее дисперсионное уравнение [2]:

_r( 1 )       /        \      Г⁽ 2 )

йл ctg r1 )у 1) +    ™ ctg(r<2)(у 2 - у 1)) - к ц^           к ц^

-

Y к

-а

I U2 2 U 2 ) у ^— ^ ^—

-

,1 ( 1 )   ^

_aa— и( ¹ )ц( 1 )) Мм —  /

- i 4 nkS- = 0 , го

где

,______________________                        U, ( n ) ²

( n)       2_P(n),,(n)   7 2        n )       n )    ^{— a} )

r = kK e -m — y ’   —  = Д -   (n)  , (n = 1,2)•

ц

При смене направления распространения волны на противоположное в уравнении (4) необходимо сделать замену ‘+’ на ‘-‘ перед M a¹ ) , ^Ц а 2 ) •

В предельном случае при ц^1) = Ma2) = 0, дисперсионное уравнение (4) переходит в соотношение для плоской активной структуры с изотропными слоями:

Г( 1)       /        \      Г(2)                                            су k-цу Ctg(r<1 )у 1) + k^jy ctg(r<2)(у2 — у 1)) — i4nkSro = О,

где r⁽ⁿ⁾ = д/ к 2 £⁽ⁿ⁾-⁽ⁿ⁾ — у ² ,  ( n = 1 , 2 ) .

Как показывает численный анализ уравнения (4), мнимая часть постоянной распространения у" ( y = Y' - i/' ') волн структуры с ферримагнитными слоями для одного из направлений больше мнимой части постоянной распространения волн структуры с изотропными слоями при прочих одинаковых условиях.

Докажем это утверждение для частного случая структуры на рис. 1 б.

Пусть у ^ = 2у и ферромагнитные слои 1 и 2 имеют одинаковые физические параметры, но подмагничены в противоположных направлениях:

н ( ¹ ) = н ² ) = а    н а 1 ) = -н а ² ) = н а ,   s ¹ ) = s ^{2 )} = =.

В этом случае уравнение (4) переписывается следующим образом:

л] к 2 £Н1 - Y ² ctgУ 17 к 2 £Н 1 - Y ² ) + ^Н Y - iAк = 0 ,    (6)

где a = 2пк 5 —, н. = Н - го

( Н а ) 2 н

Уравнение (6) для случая возмущения. Будем искать распространения в виде нормированная постоянная

a << 1, а << Н можно решить методом замедленные волны с постоянной

Y                            п

₇ = Y о ⁺ Y 1 , где Y о =   ^s H ^- ——₂

k                            ]      (2кУ1) 2

распространения в структуре без полупроводниковой пленки при а = 0. Тогда для Yi получаем выражение:

Y 1 = ±

Г Н а )

V Н У

Y о

k5Y o И ~ ^Н

- iaF ± ( н, Н а ) ,

где функция

F ± ( Н , Н а ) = H 1 I ^{k 5} Y o И ^{Н а}

- 1

V

н У

характеризует влияние гиротропии ферромагнитных слоев на коэффициент усиления волны в структуре; верхние знаки в (7) соответствуют распространению волны в прямом направлении, нижние знаки -распространению волны в обратном направлении.

Из формулы (7) следует, что в структуре существует невзаимный эффект усиления волны : в прямом направлении при а * 0 коэффициент усиления волны больше, чем в отсутствие гиротропии, в обратном - меньше.

Например, для ферромагнитного слоя с толщиной к 5 = 1 и

намагниченностью насыщения ферритов

4пМ₀ = 0.4 ^—

⁰        h о

( h 0

-

гиромагнитное отношение) при внешнем поле

H ₀ = 0,1 ^— функции F ₊ , F - , h 0

характеризующие усиление в линии, примерно равны 1.36 и 0.55. Для изотропных слоев при данных условиях F+ = F_ = 1 . Этот эффект связан с явлением смещения поля, которое имеет место в ферромагнитных материалах. При данном направлении намагничивающего поля происходит смещение поля вдоль оси у (рис. 1 б).

Дисперсионное уравнение (4) численно исследовалось на ПЭВМ методом Хука- Дживса [3], в качестве исходного приближения, для которого использовалась формула для постоянной распространения в виде :

г' 3

Y = —BA ± Re к   к5

V 2 k 5

А²           3              о-

BA]  + е       , ■ i 4 пкЗ-Д ^ ,

V        ^{( к5 )           —}

7"          Г 3    Л ²        3            О

Y = ± Imj I — BA I + е--+ i4лк§—A I, к      ^ 2к5 )     ^sf      — где A =

я Г м ?

a^

—

я ?

М?>^a ’ ^B   я ²⁾ я !²⁾

—

м^

м ¹ м ¹ •

е = е ⁽¹⁾ + е ⁽²⁾

.

Соотношения (8) получены из уравнения (4) путем аппроксимации ctg(z) « 1^ + z^. Магнитные потери в ферромагнитных слоях были учтены с помощью задания мнимой и вещественной частей компонент тензоров магнитной проницаемостей в форме Полдера [4]:

. ।     • ii ..            .    ।     ; . .и

^H = ^H i^H , H a    H a   i H a ,

h '= 1 - -A (1 - - )(1 + в )² - 2 р ²(1 + P ²)⁴

Д-1,

n" = BAU + ? ^{2  -1              2 -1} // " = 2/?^1 + R ² — 2 A^-1

H PA (1 + — )^  , Ha (1   — )^  , Ha 2p—(1 + р )  ^,

Д = (1 - -)2 + 4-2p2(1 + в)-1, - = to, A = toto to0 = h0H0, tom = h04nM0, где 4nMo - намагниченность насыщения феррита, Ho - напряженность поля подмагничивания, р - параметр, учитывающий потери в феррите, hQ - гиромагнитная постоянная.

На рис. 2-3 представлены некоторые результаты электродинамического анализа структуры, изображенной на рис. 1 б. На рис. 2 представлены результаты сравнения дисперсионных зависимостей постоянной распространения у (мнимой и действительной частей), полученной с помощью метода Дживса- Хука, с кривыми, вычисленными по формуле (8) без подмагничивания. Наблюдается хорошее качественное совпадение поведения дисперсионных кривых.

На рис. 3 приведены результаты расчетов дисперсионной постоянной основной волны рассматриваемой структуры при значении напряженности подмагничивающего поля Но равное 12 кЭ по методу Дживса- Хука. Структура обладает явно выраженными невзаимными свойствами в области ферромагнитного резонанса (рис. 3); усиление ( Im (у к<)) основной волны в прямом и обратном направлении значительно различаются ( в три-четыре раза ). Кроме того, существенно различаются и действительные значения постоянных распространения Re(yk<). Эти свойства связаны с невзаимным распределением СВЧ- поля при изменении направления распространения (подмагничивания). Если для прямой волны (направление +z) максимум поля смещается к активной полупроводниковой пленке, то для обратного направления максимум поля смещается к металлическим стенкам прямоугольного волновода. Что касается зависимостей реальной части постоянной распространения Re(y /к) от поля, то аналогичный характер они имеют для прямоугольного волновода с ферритовыми слоями без пленки /9/. При величине подмагничивающего поля Но = 12 eY усиление электромагнитной волны происходит в одном направлении в определенном частотном диапазоне; в обратном направлении распространения волна затухает.

Приведенные результаты моделирования активной структуры с ферримагнитными слоями могут быть использованы при конструировании активных устройств с распределенными параметрами и дальнейшей

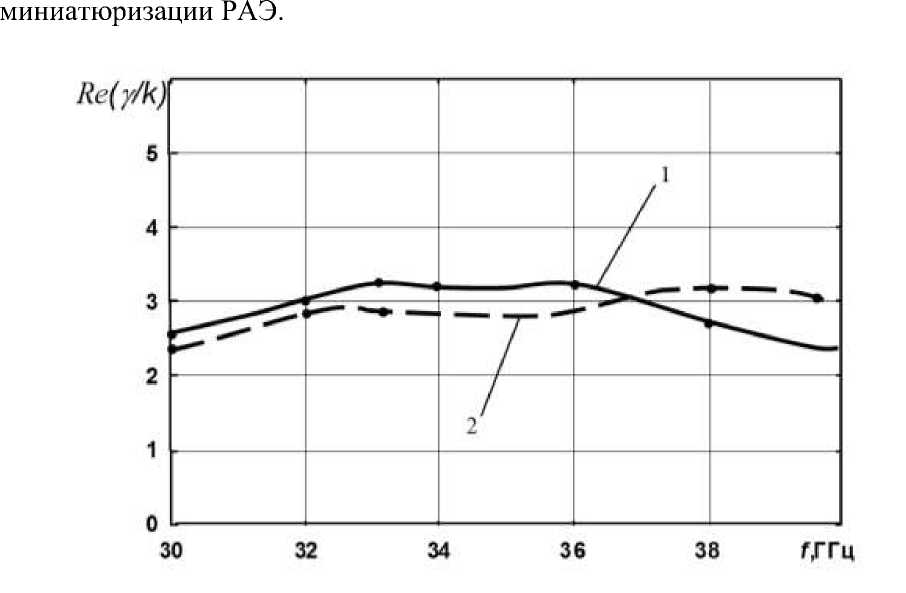
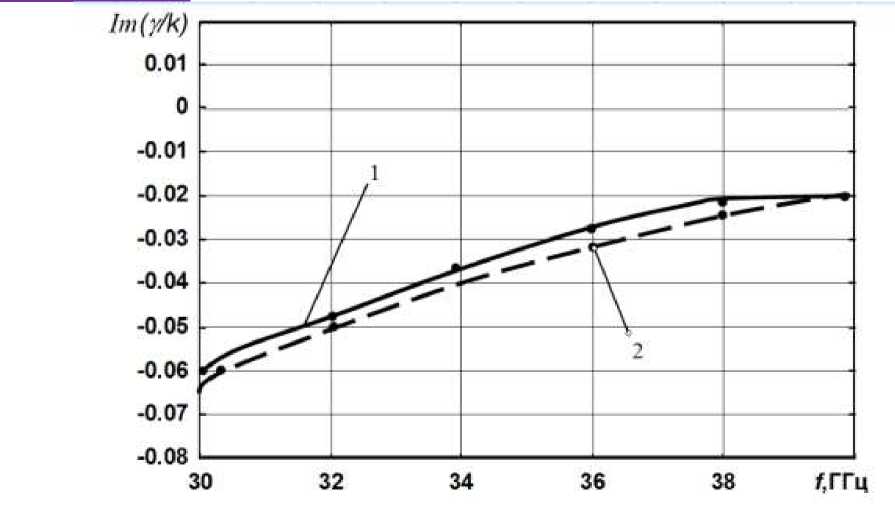
Рис.2. Дисперсионные зависимости для плоской активной структуры с не намагниченным ферритовым слоем с учетом потерь в феррите: y₂ =7.2 мм; у 1 =3.4 мм; ^ (1 =10; ^ (2 =1; к 5 =0.01; о н о =1; ^ =0.1;кривые 1 -расчёт по методу Хука-Дживса; кривые 2-расчёт по формуле (8)

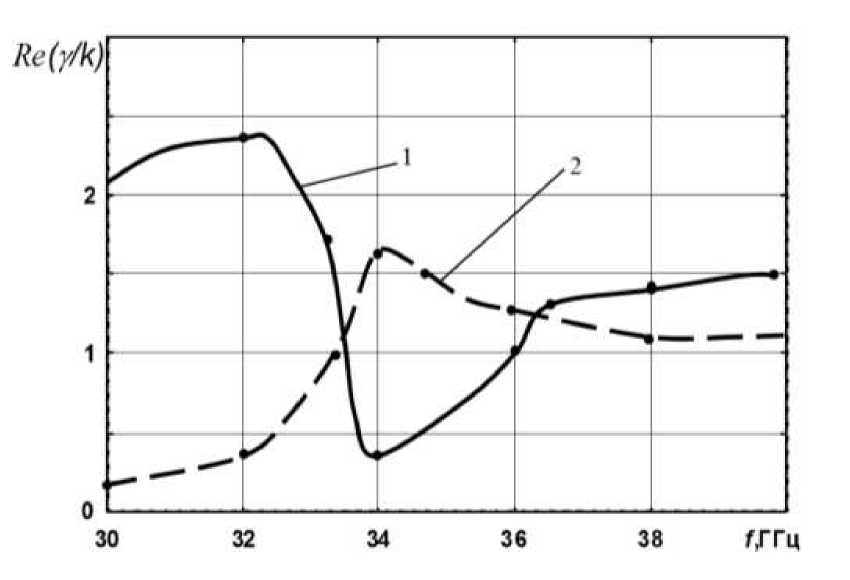
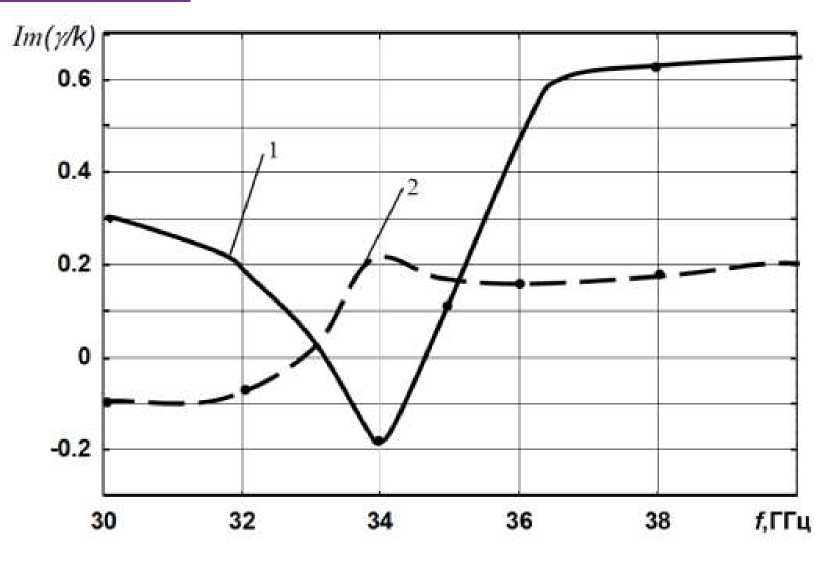
Рис.3. Дисперсионные зависимости для плоской активной структуры c намагниченным ферритовым слоем, рассчитанные по методу Хука-Дживса: H 0 =12 кЭ; кривые 1- прямое направление; 2-обратное направление; : у₂ =7.2 мм; у 1 =3.4 мм; ^ (1 =10; ^ (2 =1; k S =0.01; a / го =1; / =0.1;кривые 1 -расчёт по методу Хука-Дживса; кривые 2-расчёт по формуле (8)