Проблема ковариантности в релятивистской теории излучения

Теория релятивистского излучения является одной из самых востребованных в настоящее время физических теорий [1,2]. Об этом говорят многочисленные применения этой теории в экспериментах с поляризованными пучками элементарных частиц в физике высоких энергий, в спектроскопии твёрдого тела, в наблюдении развития химических реакций, в исследовании структуры молекул ДНК, в экологии при анализе атмосферных аэрозолей, почвы и воды, наконец, в создании новых прогрессивных технологий макроэлектропики, микромехапики, конструировании новых композитных материалов и так далее.

Основы теории релятивистского излучения и, в частности, синхротронного излучения были разработаны во многом благодаря работам российских физиков-теоретиков — В. В. Владимирского, Д. Д. Иваненко, А. А. Соколова, И. М. Тернова и других учёных из научной школы Московского и Томского государственных университетов [3,4]. Следует отметить также работы ряда, выдающихся зарубежных физиков, таких как Г. А. Шотт, Ю. Швингер и других.

В настоящее время основные свойства релятивистского излучения хорошо известны и находятся в прекрасном согласии с экспериментом. Тем пе менее, отдельные элементы этой теории могут быть ещё усовершенствованы, например, с использованием более строгой атрибутики специальной теории относительности, которая лежит в основе теории релятивистского излучения.

В данной работе показано, в частности, что применение ковариантных методов теории релятивистского излучения позволяет значительно упростить интегрирование углового распределения излучения произвольно движущихся релятивистских заряженных частиц, что позволяет более глубоко и просто проанализировать происхождение электромагнитной массы и силы радиационного трения, а также попять причину появления аномального магнитного момента, электрона в рамках чисто классической теории излучения.

Разумеется, в данном направлении вели исследования и другие авторы, включая известные работы Х.Д. Баба. [5], П. Калдирола. [6,7], К. Тейтельбойма. [8] и других [9-11]. Мы надеемся, что представленные здесь оригинальные результаты окажутся также полезными и интересными.

1. Полевая динамика заряженной частицы с учётом внешних полей и полей, создаваемых произвольно движущимся релятивистским зарядом

Известно, что в теории поля четырёхмериый вектор плотности силы, действующей на. заряженную точечную частицу, определяется соотношением

F e¹ (^^р) = m₀c I dTw^p(T)5 [£^p — r^p (t )] .

(1.1)

Здесь четырёхмерный вектор Д' = (ct, £) описывает произвольную мировую точку вблизи от радиус-вектора заряженной частицы г ^р (т ), которая движется с четырёхмерной скоростью v ^p ( t ) и ускорением w ^p ( t ). Из этого определения следует, что импульс частицы связан с плотностью силы соотношением

РД(т ) = - I F ee (П dY = mov^(T ),

(1.2)

где dY = d4^p — элемент четырёхмерного объёма. Используя стандартное определение силы Лоренца

Fe = -H^_v ( t ) = mow^(T )

(1.3)

и четырёхмерного вектора плотности тока

je К^Р) = ec j dT^ (т )5 [£^р - г^р(т)] ,

(1.4)

выражение для плотности силы (1.1) можно представить в виде

Fe¹ (^) = ¹H"_tJve Г) = (¹ ( jE ext) , p E ext + ¹ [ jH ext]) ^e c ^ex               c                     c

.

(1.5)

Интересно, что эти формулы можно получить так же, используя уравнения Максвелла.

fl rrM^v _   -д ^dv Hext = c Je

(1.6)

и тензор плотности энергии-импульса заряженной частицы

E^pvГ) = moc I ^(т )v^V (T )5 [^ - r^p(т)] dT,

(1.7)

при этом

µ       µν        µν

J e      v^e          v^ext,

(1.8)

где нов столу д, обычно

*V = д^’ а тен30Р плотности энергии-импульса внешнего поля определяется как

E exVt = —   (#^pvH ^p + ¹ <'ПH^aA .

4П \          4

Таким образом, мы приходим к дифференциальному закону сохранения тензора, плотности энергии-импульса dv Е^ + dv Е^ = 0.

(1.10)

В более общем случае с учётом самодействия электромагнитных полей, излучаемых самим зарядом, будем иметь dv Е; + dv Eex + dv е^ = 0.

(1.11)

Характер производной d_v ещё нуждается в уточнении (см. ниже). Сам тензор Е^^ состоит из трёх слагаемых:

^^^^в

1-W

^^^^в

1-W

Е^ = Еpv + Еpv + Е pv,

(1.12)

которые соответствуют тензору плотности энергии-импульса конвективных полей, создаваемых вблизи заряда (~ 1/r4):

1    e2c4                                                 1

Е' =---д < c²r^pr^v + r_pv^p (r^pv^v + r^vv^p)-- g ^pv (r_pv^p) > ,             (1-13)

4n (r pvp)6 I                                        2'              J тензору плотности энергии-импульса смешанных полей, создаваемых в ближней и дальней зонах излучения (~ 1/r3):

bS#

^^^™

Е ^pv =

1   e2c2

^4п (r_p v ^p )3

!

r_pw ^p (rV + r^vv^p) (rpV^p)²

2c2 r _n w ^p r ^p r ^v +---- в ^P .3

(rpVp)

r ^p w ^v + r ^v w ^p r_p v ^p

,

(1.14)

и тензору плотности энергии-импульса электромагнитного излучения в дальней зоне (~ 1/r3):

bS#

Е ^pv =

1 e2

4п (rpvP )²

J c ² (r_pw^p)2 ( ^(rP^vP)4

-Ww,   r ^p rv .

(rPvP) J

(1.15)

Здесь повсюду Г^р = (r, r) — светоподобный четырёхмерный радиус-вектор, проведённый из мировой точки заряда в точку наблюдения.

Однако вернёмся к интерпретации третьего члена, в дифференциальном законе сохранения тензора, энергии-импульса (1.11).

• 2.    Проблема запаздывания излучения в точке наблюдения

Специфика полей, издаваемых зарядом в Е^р состоит в том, что они определяются в запаздывающий момент времени

r t = t + -.                                             (2.1)

Однако во всех членах формулы (1.11) ковариантное дифференцирование, очевидно, должно выполняться в один и тот же момент траекторного времени t(r ). В связи с этим проблема дифференцирования плотности энергии-импульса Е^^ в (1.11) нуждается в переопределении.

Этот вопрос мы рассмотрим па. примере импульса, электромагнитных полей, излучаемых произвольно движущейся заряженной релятивистской частицей. Согласно формулам (1.2) и (1.9) для чистого излучения будем иметь:

Cif = - / F tif ' )dY = - У dv Е^ (t)dY,                    (2.2)

причём элемент объёма dY здесь берётся в окрестности точки наблюдения. Характер зависимости E self (t) существенным образом проявляется при интегрировании по четырёхмерному объёму с применением теоремы Остроградского-Гаусса. Поэтому в подинтегральном выражении (2.2) эта зависимость должна учитываться в явном виде.

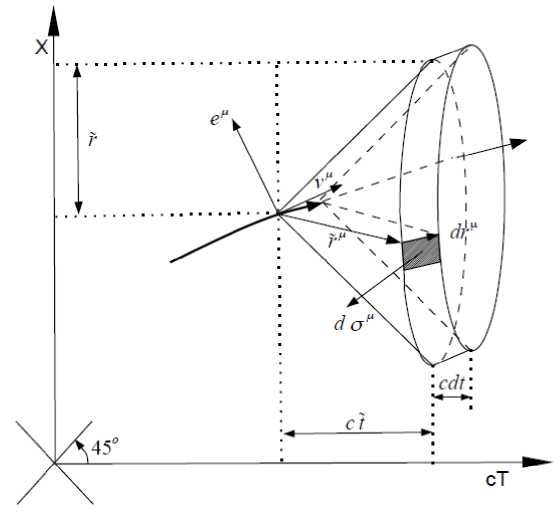
Рис. 1. Область интегрирования по пространственно-подобной гиперповерхности в виде гиперполоски

Так как всё излучение, испускаемое заряженной частицей за время dr, распространяется только внутри двух близко расположенных световых конусов (см. рис. 1), то согласно теореме Остроградского-Гаусса, всё объёмное интегрирование сводится к одному поверхностному по окаймляющей световой конус гиперполоске с элементом поверхности do”. В результате с применением теоремы Остроградского-Гаусса в четырёхмерном пространстве полный импульс излучения для всех полей, создаваемых зарядом, согласно (2.2), будет равен

Pself ^Ц j£^f ^-(2.3)

Таким образом, определение поверхности doa является важнейшей задачей для всех дальнейших расчётов. С этой целью четырёхмерный объём dT, который, как известно, является инвариантной величиной, представим в виде dY = doadRa.(2.4)

Здесь четырёхмериый радиус-вектор

Ra = ra + Га(2.5)

в общем случае соответствует мировой точке наблюдения с учётом движения заряда. С другой стороны, в системе покоя частицы элемент четырёхмерного объёма dY0 = e2ded^0 cdT = dY,

(2.6)

где e = r0 — расстояние от заряда, до паблтолатсстя в системе покоя с телесным углом dfi0. Поскольку телесный угол d^o преобразуется как d^0 =

dfi

Y² [1 - ( п в)]’

(2.7)

a e как нулевая компонента светоподобиого вектора r^ = (r, r) в системе покоя преобразуется как e = rY [1 — (пв)]

¹ r λ v ^λ ,

c

то

E2dfio = r² d^ = inv.

(2.9)

Отсюда следует, что, согласно (2.6), всё запаздывание во времени, связанное с излучением в элементе объёма dY, сводится к величине de(t), которую с помощью известных правил дифференцирования функций с запаздыванием аргумента можно определить как где

de^

∂ε дГа

dR α ,

*- t

(2.Ю)

д dra t

(+

\ dr а

г^а d r_pv ^p dT

(2.П)

Кроме того, так как, согласно (2.5), dRa = (va

+ -еедш c

'^Лk_a^ dT + k_ade,

(2.12)

где ep = k^--, epv^ = 0, epe^ = 1                              (2.13)

— пространственноподобный единичный вектор Рорлиха [12], а

µµ

(2.14)

k^ = — =--, k^k„ = 0

e      rpvp      M

— светоподобпый четырёхмерный вектор, находим

∂ε дГа

= ea

*- t

1 1 + -2 ee\w^ + сз v ^a e\w ^X .

(2.15)

Для проверки этого выражения можно убедиться, что с учётом (2.12) соотношение (2.10) тождественно выполняется. Наконец, согласно условию иивариантиости элемента четырёхмерного объёма dY = dYo на основе определений (2.4) и (2.6), а также принимая во внимание (2.10), (2.12) и (2.15), получаем daa = e2 (ea + kpwpka) d^ocdT.                            (2.16)

Этот элемент гиперповерхности в теории излучения хорошо известен в литературе. Он лежит в основе всех дальнейших ковариантных выражений в теории релятивистского излучения.

• 3.    Угловое распределение мгновенной мощности релятивистского излучения

Импульсные характеристики углового распределения релятивистского излучения можно получить с помощью (2.3), если туда, подставить элемент гиперповерхности (2.16). Тогда, получим

Pself = ^ Eself (ev ⁺ c2 ^kpw ^P kv )

r ² dUcdT.

(3.1)

Поскольку расстояние от заряда до точки наблюдения r от углов не зависит, то мощность четырёхмерного импульса, углового распределения произвольно движущегося релятивистского заряда. в единицу собственного времени примет вид

„ Г / р          х sf = r ^ Eseelf (ev - -2kpWpkv) d^.                         (3.2)

Если рассматривать далее только чистое излучение в волновой зоне то согласно (1.15), имеют место соотношения

В результате мы получаем

E ^rv rv = E ^rv kv = 0.

1-W

dP ^µ

= r dτ

£ E^rv evdU.

Подставляя сюда E ^rv из (1.15), для излучения в чистом виде будем иметь

dP ^r е²   / w_pw ^p — (e_pw ^pp2

dT     4nc² J      (n_pv ^p )‘2

(e“ ⁺ t) ®'

Здесь мы ввели совокупность четырёх светоподобных величин rp np = — = (1, n) .

r

При ц = 0 из выражения (3.6) с учётом запаздывания излучения

Л* dt dt

nρv ^ρ cγ

= 1 — ( п в)

получим мощность мгновенного излучения

W =

— / E^0v ev dU = ^γ

4П у E ² [1 — ( п в)] du,

(3.4)

(3.5)

(3.6)

(3.7)

(3.8)

(3.9)

где E — напряжённость электрического поля излучения, которая определяется компонентами (1.9).

Заметим, что эта величина, определена как потери энергии заряда на. излучение в единицу траекторного времени 1. Если же в (3.9) для измерения этого излучения использовать время наблюдателя t. то поскольку

4 = [1—( п в)] 4 dt                  dt’

(3.10)

(З.П)

соответствующая интенсивность излучения будет определяться как

I = — ф E 2du.

4п

Это выражение более удобно для спектрального анализа излучения, в котором время t является немой переменной, более подробное обсуждение этих вопросов и связанных с ними проблем можно найти в работах [13-15].

В явном виде, согласно (3.6) и с учётом соотношений (2.13) и (3.7), угловое распределение импульса, излучения в единицу собственного времени можно представить в виде

1S# dPµ dτ

=

4nc4 J

γn ^µ

[1 — ( п в )]5

{а² [1 — ( п в)]2 — ( па )²(1 — в2) + 2( па )(в а ) [1 — ( п в)]} dU,

(3.12)

где а — трёхмерное ускорение заряженной частицы. При ц = 0 отсюда в явном виде следует выражение для углового распределения мощности

dW е² а² [1 — ( п в)]2 — ( па )²(1 — в²) + 2( па )(в а ) [1 — ( п в)] dU    4пс3                       [1 — ( п в)]5

.

(3.13)

Всестороннее исследование этого выражения, а также свойства линейной поляризации излучения произвольно движущегося заряда были проделаны в работе [16].

Чтобы получить полную мощность излучения, надо проинтегрировать выражение (3.13) по углам сферической системы координат, в которой

dfi = sin 9d9d^, п = (sin 9 cos ^, sin 9 sin ^, cos 9) , ( п в) = в sin 9, ( па ) = a(sin 9 cos у sin a + cos 9 cos a), (в а ) = ва cos a.

(3.14)

После простых, по довольно трудоёмких вычислений угловых интегралов приходим к выражению (см. также [1])

W = 3 e3 (a2 - |ва]2)Y 6.

(3.15)

• 4.    Техника ковариантного интегрирования углового распределения излучения

Те же результаты, по физически и математически более изящным методом можно получить с применением ковариантного интегрирования углового распределения релятивистского излучения. Отправной точкой здесь являются простые инвариантные угловые интегралы. Например, с2 / dn

(4.1)

4п J (npVp)2     ’ значение которого фактически является следствием иивариаитиости соотношения (2.7) для телесного угла.

dn = С2 (n^fd^.

(4.2)

Более сложный интеграл при наличии в подиитегральиом выражении вектора. Рорлиха. (2.13) будет иметь один единственно возможный вариант ответа dan-^-- = Cvp.

(4.3)

4п       (npvp)2

Постоянную C1 можно определить из ковариантных соображений, умножив обе части (4.3) на четырёхмерный вектор скорости v^p. Поскольку v_pe ^p = 0 и v_pv ^p = -с², то остаётся только припять Ci = 0. Точно так же вычисляется утло вой интеграл с двумя векторами е^м, который можно представить в виде

I2 / an^-^ = C0

(4.4)

Можно определить постоянные коэффициенты Co и C₂, домножив равенство (4.4) на множители g^v и v_pv_v, после чего появляются два простых уравнения

/ 4C0 - C2 = 1(4.5)

Co - C2 = 0, из которых следует, что Co = С2 = 1/3, и, стало быть, интеграл

I2 / an= 1 Gpv.(4.6)

4п J     (npVp)23

Здесь мы ввели новое обозначение

G^, = g^, + 1 v^vv.^^

c2

Аналогичным образом вычисляются интегралы с большим числом множителей epevep ..., однако при этом возникает проблема симметризации окончательного ответа по индексам ц, v, р,... (для одного и двух множителей epev такой проблемы вообще не существует). Но теперь в случае трёх множителей epevep ответ следует записать в виде c2

4п J

µνρ an -——

(npVp)2

= ¹ Ci (g^pvv^p + g^ppV + g^vpv^) + 4C^v"v^p, c                                     c³

а. при четырёх e^pe^ve^pe^X — как

2    µνρλ

— / dU ---— = Co g^pvg^pX + g^ppg^vX + g^^Ag^vp +

4n J      (npV^p)2 ^{v                               7}

(4.9)

+ 4C2 (g^^vv^pv^X + g^Mpv^vv^X + g^^Xv^vv^p + g^vXv^pv^p + g^pXv^v^v) +4C4v^pv^vv^pv^X.

c2                                                                        c4

[ 3C1 - Сз = 0,

и

( 24Co - 12С2 + С4 = 1,

-6С0 + 9С2 - С4 = 0,                               (4.11)

(  3Co - 6С2 + С4 = 0.

Решением этих уравнений является С1 = С3 = 0 и С0 = С2 = 1/15, С₄ = 1/5. Таким образом, интеграл с нечётным числом векторов Рорлиха снова равен пулю, а с четырьмя — представляется в виде

— I dU e"^- e^P-^X 4n J     (npv^p)²

= 115 G(pv GpX).

(4.12)

Здесь G^^v определяется соотношением (4.7), а круглые скобки означают симметризацию по всем индексам

G^(pv G^pX) = G^pvG^pX + G^ppG^vX + G^pX G^vp.

(4.13)

Дальнейшие расчёты показывают, что все интегралы с нечётным числом векторов Рорлиха. всегда, обращаются в пуль, а с чётным — принимают простой и красивый вид, например, с2 7 dU -PeVe^-0-^

4п J         (npvp-)2

= — G(pv GpXGCTn). 105

(4.14)

Разработанная здесь техника, ковариантного интегрирования углового распределения релятивистского излучения применяется не только для изучения произвольно движущегося заряда, по и более сложных источников излучения, например, таких как собственный магнитный момент электрона [17].

С применением к излучению заряда согласно определению мощности импульса. (3.6) и с учётом известных формул (4.2) и (4.6) получаем

1S.

dP^µ dτ

2-2 р р

3^5 wp w^p<

(4.15)

откуда при ц = 0 сразу следует уже известная формула (3.15) для мощности излучения в единицу собственного времени

W = ²4wpw = I4 (^a2 ^- [^eal2) Y6.

(4.16)

3 c3         3 c3

• 5.    Излучение в ближней зоне, сила радиационного трения и аномальный магнитный момент электрона

Формула, для мощности импульса, чистого излучения (4.15), как и должно быть, не зависит от расстояния между зарядом и наблюдателем. Однако, если мы хотим учесть влияние электромагнитных полей, излучаемых зарядом, па. динамику его движения, то надо перейти к рассмотрению этих полей в непосредственной близости от заряда, где существенным становится не столько влияние поля излучения, входящего в тензор E”v(~ 1/r2), сколько влияние конвективных полей в E ”v (~ 1/Г4). а. также смешанных по.лей. образующих тензор E”v(~ 1/r3).

Если па. основе определений этих тензоров в (1.13)—(1.15) с применением техники ковариантного интегрирования угловых распределений к формуле (3.2) найти мощность соответствующих им импульсов в единицу собственного времени, то получим dP” = 0 - 1 ^2 “” dT        6 ec2

µ dP dτ

2 e2

-— w” + 0, 3 ec²

*< dPµ dτ

2 e²

—- w_aw^av” + 0.

3 c⁵

(5.1)

(5-2)

(5.3)

Порядок написания членов в правой части этих формул соответствует их очерёдности в определении элемента гиперповерхности da_a в (2.16). В динамике излучающего заряда все эти выражения следует брать с противоположным знаком (то, что заряд излучает, соответствует потерям энергии).

Таким образом, силу самодействия излучающего заряда можно определить в виде dP”   dP1”   dP”\     2 e2             3 c3

• ^F“lf = - (— ^{+    +}      = -3c5 (w-w v” ⁺ 4Tw”) •          ^,5-⁴’

Однако при подстановке этого выражения в уравнение движения заряда во внешнем поле (1.3) следует учесть, что заряд «почувствует» влияние излучаемых им полей не сразу, а спустя лишь очень маленький промежуток времени Дт, равный по порядку величины времени отделения электромагнитного поля от заряда e/c, если в качестве e принять классический радиус электрона (см. [18] и др.)

e²

e = — c2. 2m о

(5.5)

Здесь mо означает электромагнитную массу электрона, которая отличается от инертной (см. ниже).

Более того, величину Дт можно определить из физических соображений. Действительно, наиболее существенно отставание силы самодействия проявляется во втором члене FSef в (5.4). Поэтому именно здесь следует сделать замену dwµ w” ^ w”---—Дт.                               (5.С)

dτ

Но так как для силы самодействия должно выполняться условие прострапствеппо-подобия

(5.7)

V” F”lf = 0, то с привлечением стандартных соотношений специальной теории относительности V”V” = —c2,

V”W” = 0 получаем д 4 e 2 e2

(5.8)

3 c   3 m 0 c²

В литературе эту величину называют также хрононом (см. [11,19] и др.) или квантом времени.

Теперь выражение для FSef примет вид

”     2 e2 dw”    1                e2

Fell = 3 c3 (- 72 waw v”) - .                            ¹⁴'’'

Если эту силу объединить с силой Лоренца (1.3), то получившиеся при этом уравнения движения можно переписать в виде e2          e          2 e2 dw”

c2 w wαvµ  .

(5.10)

(^m0     . ' ^w” = c^H” vv ⁺ 3c3 (S7^—

В этой формуле к обычной традиционной массе заряда mo добавляется член с электромагнитной массой, которая появилась в (5.5)

e2

(5.П)

m⁰ = W.

Эта величина, существенно зависит от классического радиуса электрона, который совпадает с радиусом сферически симметричного электромагнитного поля, отделившегося от заряда.

Однако в наших рассуждениях отсутствует ещё один важный элемент событий, происходящих па. микроскопическом уровне вблизи электрона — это индикатор масштаба, наблюдаемых событий. Таким индикатором с учётом квантовых процессов является, как известно (см. например, [18]), комптоновская длина волны электрона

2пН

(5.12)

Лк =----.

m0 c

В связи с этим естественно принять значение с с учётом (5.1) равным

Но тогда.

1 ^     пН

2 k   moc2m

1 е2

mo = тг ~'m = д-mo, 2п Нс2п

(5.13)

(5.14)

где а = е²/Нс — постоянная тонкой структуры.

Заметим, что такое значение электромагнитной массы электрона для слабых полей встречается и в более строгой квантовой электродинамике (см., например, [20]).

Таким образом, уравнение движения заряда (5.10) с учётом самодействия электромагнитных полей и при наличии внешнего поля принимает вид где

_m∗₀

∗ µ ^e µν µ ^m0^w = cHext ⁺Frad,

mo + mo = mo (1 + 2^)

(5.15)

(5.16)

— динамическая масса заряда, а

µ rad

2 е² / dw^

3 с³ \ dT

С2 Wa W^aV^

(5.17)

— хорошо известная в литературе [1,2] сила радиационного трения. Заметим также, что если mo — это наблюдаемая масса, электрона, то собственный магнитный момент электрона, или магнетон Бора, с учётом (5.16) будет равен еН

Mo = д--- 2moc

(1 + ^ = Mo + Ma, 2mo с \    2п/

(5.18)

что означает, кроме наблюдаемого магнитного момента Mio, наличие ещё и аномального магнитного момента, электрона, который в своё время был вычислен [21] и подробно обсуждался в квантовой теории [22-24].

Заключение

В данной работе мы показали, что ковариантные методы интегрирования углового распределения релятивистского излучения позволяют очень просто получить не только интегральные характеристики этого излучения, по и найти их естественную связь с уравнениями движения заряда. Сам этот факт имеет элементарное физическое объяснение, которое заключается в том, что ковариантные вычисления соответствуют структуре математического аппарата классической электродинамики, основанной па. специальной теории относительности.

К сожалению, изначально ряд работ в этом направлении был выполнен в пековариаптпой форме, что привело к большой путанице в определении основных характеристик излучения и силы радиационного трения (более подробно об этом см. в [25,26]). Заметим также, что физическая экзотика феномена силы радиационного трения иеодиократио приводила, к появлению ряда, совершенно неординарных гипотез и предположений (см. [6,7,9-11,27-32] и др.), которые до сих пор заслуживают тщательного изучения. В связи с этим простая и физически обоснованная постановка. задачи об излучении произвольно движущейся релятивистской частицы приобретает особо важное значение.

Перечислим ещё раз основополагающие идеи предлагаемого здесь ковариантного метода, вычислений в теории релятивистского излучения произвольно движущегося заряда.

• 1.    Повсюду на. всех этапах вычислений задействован ковариантный формализм специальной теории относительности в четырёхмерном пространстве Минковского.

• 2.    При взаимодействии заряда с электромагнитным полем учитывается как внешнее поле, так и поля, создаваемые самим зарядом, включая конвективное поле вблизи от заряда, поле излучение в волновой зоне, а также смешанное поле, обусловленное интерференцией двух предыдущих полей.

• 3.    В соответствии с принципом причинности при определении силы взаимодействия заряда с собственным электромагнитным полем учитывается запаздывание во времени полей, излучаемых зарядом.

• 4.    Установлено, что движение заряда является следствием единого закона сохранения для тензоров плотности энергии-импульса всех электромагнитных полей, взаимодействующих с зарядом, в дифференциальной форме.

• 5.    Уравнения движения заряда с учетом собственной электромагнитной массы и силы радиационного трения могут рассматриваться как следствие применения теоремы Остроградского-Гаусса. в четырехмериом пространстве к закону сохранения суммы всех тензоров плотности энергии-импульса. Техника ковариантного интегрирования угловых распределений излучения произвольно движущегося заряда значительно упрощает процедуру получения этого результата.

• 6.    Окончательный вид уравнений движения получается после приведения всех сил, действующих па. заряд, к одной мировой точке, где в данный момент собственного времени находится этот заряд.

• 7.    После получения уравнений движения с учётом силы радиационного трения электромагнитная масса, произвольно движущегося заряда получает наглядную физическую интерпретацию, которая, как оказалось, связана с аномальным магнитным моментом электрона.