Проблема неопределенности параметров прочности при численном моделировании динамического разрушения известняка

Большая практическая значимость и распространенность известняка как природного конструкционного материала привела к большому числу работ, посвященных его механическим свойствам (см., например, [1–3]). Подавляющее число этих работ имеет дело с различными условиями медленного квазистатического разрушения, и только малая их часть посвящена разрушению известняка при динамических условиях нагружения [4, 5]. Как правило, исследования проводятся по стандартной методике на стержне Гопкинсона–Кольского [6, 7]. Преимуществом этой методики является независимое измерение при помощи тензодатчиков деформации (и пересчитываемых по ней напряжений) в падающей, отраженной и прошедшей через образец ударных волнах.

Пористость известняка, в отличие от многих других материалов, позволяет просто модифицировать его внутреннюю структуру и изменять механические свойства путем насыщения пор водой или маслом. В динамическом режиме, как показали недавние эксперименты группы А.М. Брагова [4, 5], это может, в зависимости от скорости деформации, приводить либо к уменьшению, либо к увеличению динамической прочности известняка. Для описания подобного эффекта потребовалось изменить обычный для статики подход к критерию прочности как пороговому напряжению, достаточному для разрушения материала,

и использовать интегральный критерий прочности с дополнительным параметром инкубационного времени [4, 5, 8, 9], учитывающим в данном случае эффект влагонасыщенности материала. Величины этого параметра для образцов известняка были определены при помощи моделирования в одномерной постановке в работах [4, 5]. При этом, как было показано в [10, 11], имеются значительные проблемы как с корректной обработкой экспериментальных данных для получения истинного профиля волны напряжения в образце, так и с точностью измерения самих механических характеристик нагружаемого материала. Последнее обстоятельство не позволяет при численном моделировании в полной мере исследовать более тонкие эффекты, возникающие вследствие влагонасыщенности образцов.

В данной работе на основе трехмерного численного моделирования с простой — квазистатической — моделью процесса разрушения известняка делается попытка определить по имеющимся экспериментальным данным соответствующие параметры материала, и обсуждаются проблемы, связанные с этим определением.

• 2.    Постановка экспериментальных исследований по ударному нагружению образцов из известняка на стержнях Гопкинсона–Кольского

В экспериментах [4, 5] исследовалось динамическое нагружение известняка с порами на стержне Гопкинсона–Кольского с различными скоростями ударника (от 3,5 м/с до 17,5 м/с). На рисунке 1 показана используемая в расчетах модель, которая имела параметры, аналогичные экспериментальной установке, и представляла собой два коаксиальных длинных стальных стержня с ударником, соударяющимся с левым стержнем. Для отсечения нежелательных эффектов и обеспечения условий одноосности деформации длина стержней во много раз превосходила размеры образца (мишени) и ударника. Все элементы конструкции были цилиндрической формы. Образец с порами закреплялся при этом между стержнями. Объемная доля пор в образце составляла около 5%. При ударе по левому стержню начинала распространяться волна сжатия, которая после достижения нагружаемой поверхности мишени разделялась на прошедший импульс сжатия и отраженный от ее тыльной стороны в обратном направлении импульс растяжения. Прошедшая через образец часть импульса сжатия продолжала движение вдоль второго стержня.

Рис. 1. Численная модель экспериментов на разрезном стержне Гопкинсона–Кольского по динамическому нагружению образцов из известняка

В таблице приведены основные параметры модели процесса разрушения. В качестве материала стержней и ударника использовался известный алюминиевый сплав Д16 (дюралюминий). Его параметры были следующими: плотность — 2800 кг/м3; модуль Юнга — 72 ГПа; коэффициент Пуассона — 0,33. В модель образца из известняка внедрялись 19 пор диаметром по несколько миллиметров, так что их объемная доля была близка к экспериментально измеренным 5%. Рассматривалось два случая: 1) поры заполнял воздух с плотностью 1,2 кг/м3 (сухой образец); 2) поры содержали жидкость с плотностью 1200 кг/м3 (влагонасыщенный образец).

Как известно, все природные материалы имеют большой разброс физико-механических характеристик, которые для разных образцов, взятых из одной и той же выборки, могут отличаться на порядок и более. Это создает существенные сложности и неопределенность при исследовании материалов, даже прошедших процедуру аттестации типа ГОСТ. Одна из проблем состоит в том, что по всем стандартам дляопределения свойств берутся большие объемы материала, которые ввиду существенной степени неоднородности структуры могут совершенно отличаться от вырезаемых для экспериментального исследования образцам-«таблеткам» диаметром, не превышающим пару сантиметров. Как показывают расчеты, при динамическом режиме нагружения это обстоятельство может оказаться критическим.

Далее в таблице приведены параметры установки типа Гопкинсона–Кольского, применяемой в экспериментах [4, 5], и данные о динамической прочности известняка, пересчитанные в [10] на основе

Таблица. Параметры, используемые при моделировании процесса динамического разрушения

Диаметр стержней и образца d , мм Длина образца L , мм Длина стержней/ ударника, мм Статическая прочность известняка на сжатие, МПа Модуль Юнга известняка E, ГПа Скорость звука в известняке cs , м/с Плотность известняка ρ , кг/м3 Динамическая прочность согласно [4], МПа согласно [10] ГОСТ 20 14,5 1500 / 300 11,3 более 25 10 2030 2430 20–90 этих же экспериментальных параметров. Очевидно, что для испытываемого строительного известняка вычисленные значения получились в несколько раз меньше, чем соответствующие величины по ГОСТ.

• 3.    Численное моделирование задачи, аналогичной экспериментальным исследованиям

Для проведения трехмерного численного моделирования была создана трехмерная модель ударника, обоих стержней и образца с порами (см. Рис. 1, 2). Численные эксперименты полностью соответствовали натурным [4, 5]. Динамическое нагружение при моделировании задавалось путем придания начальной скорости ударнику, который при соударении с левым стержнем генерировал в нем ударную волну (Рис. 3), отражавшуюся от свободной поверхности ударника и в дальнейшем, многократно, от боковых поверхностей ударника, стержней и образца. Последнее обстоятельство приводило к тому, что на профиль волны напряжений накладывались значительно меньшие по амплитуде колебания (см. Рис. 3). Так как ударник и стержень были сделаны из одного и того же материала, то переотражения волны от нагружаемой поверхности стержня при ударе не происходило. Материал стержней считался чисто упругим, и при прохождении по стержню ударной волны диссипация энергии волны отсутствовала.

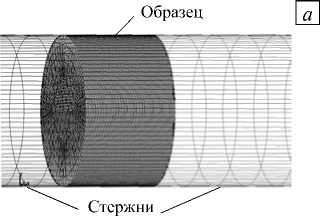
Рис. 2. Модель нагружаемого образца ( а ) с внедренными в него порами ( б )

t = 0,013 мс

а

0,043 мс

0,068 мс

0,168 мс

0,298 мс

0,319 мс

0,468 мс

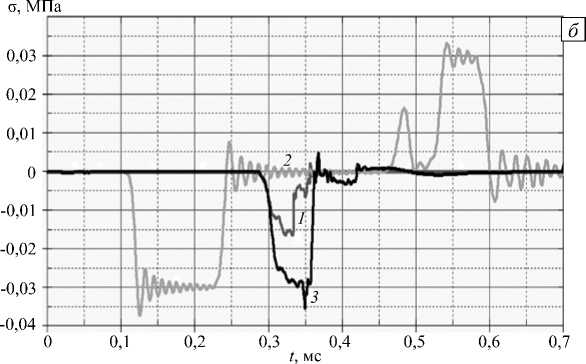
Рис. 3. Распределение продольных напряжений в нагружающих стержнях и образце ( а ) и характерные профили волн при начальной скорости ударника 3,5 м/с: волны, прошедшей в середине образца (кривая 1 ); волн падающей и отраженной от образца ( 2 ), а также волны вблизи левого, ближнего к ударнику, торца образца ( 3 )

Расчеты осуществлялись с помощью коммерческого пакета конечно-элементного моделирования задач динамики LS Dyna [12]. В программе на каждом временном шаге численно решалась стандартная система уравнений механики сплошной линейно-упругой изотропной среды [12]. На всех поверхностях стержней и образца задавались граничные условия свободной границы. Считалось, что после формирования волна распространялась по стержню с постоянной скоростью в направлении образца, а при взаимодействии с ним разделялась на отраженную и прошедшую волны.

На рисунке 3 представлены изображения всей исследуемой системы и распределение напряжений σ в ударнике, стержнях и образце в различные моменты времени для разных начальных скоростей ударника. Доля прошедшей и отраженной энергии волны напряжения зависела от соотношений упругих модулей и плотностей стержня и образца.

Важно отметить, что ширина импульса напряжения в экспериментах на стержнях Гопкинсона–Кольского во много раз превосходит размеры исследуемого образца (см. Рис. 3 а ), за счет этого удается добиться условий нагружения с практически постоянной амплитудой внешнего воздействия. На рисунке 3 б показаны падающая, отраженная волна в середине образца, а также волны в образце: первая — падающая и прошедшая через образец; вторая — в центре образца; третья — у нагружаемой поверхности).

Прошедший импульс напряжения (измеряемый в дальнем от ударника — правом — стержне), в общем случае аналогичен импульсу, проходящему по образцу. При этом он оказывается более сглаженным, максимумы импульса в образце и импульса прошедшего могут отличаться. Импульсы давления в сухом и влагонасыщенном материале с крупной пористостью, как показала серия расчетов, выполненных при разных скоростях ударника, по амплитуде отличаются незначительно (в сухом — на несколько процентов больше), поэтому в дальнейшем при сравнении различных мод разрушения известняка будет подразумеваться только влагонасыщенный материал. Отчасти такой выбор обусловлен тем, что заполненные влагой поры мало деформируются, и это значительно облегчает моделирование процесса разрушения.

Прохождение волны напряжения по образцу сопровождается его деформацией и последующим разрушением (Рис. 4). Доля энергии в прошедшей и отраженной от образца волнах распределяется в зависимости от степени разрушения исследуемого образца. Математическая модель разрушения, используемая в программе (ориентированные трещины), предполагает, что разрушение происходит при условии, когда максимальные главные напряжения превышают критическое значение, причем конечный элемент разрушается в плоскости, перпендикулярной этим максимальным напряжениям. Нормальные и сдвиговые напряжения в этой плоскости внутри элемента уменьшаются до нуля постепенно — в течение нескольких временных шагов. В дальнейшем элемент может разрушиться и по другим плоскостям (изотропно) и стать в итоге жидкоподобным, но сохраняющим упругие свойства на сжатие. Модель хорошо представляет процесс разрушения керамик и пористых материалов, где эффекты упрочнения с ростом давления незначительны.

На рисунке 4 показаны зависимости напряжения от времени и картины разрушения влагонасыщенного образца в фиксированные моменты времени. Как и на рисунке 3, приведены волны вблизи ближнего к ударнику — левого — края образца (кривая 1 ) и в его середине (кривая 2 )

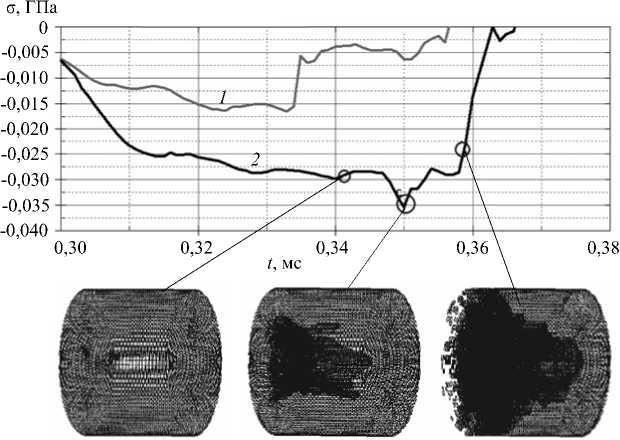
Рис. 4. Распределение напряжений с течением времени во влагонасыщенном образце и картины его разрушения в различные моменты времени

• 4.    Сравнение расчетного профиля прошедшей через образец волны с экспериментальным при различных скоростях ударника: разные пределы прочности и чисто упругий случай

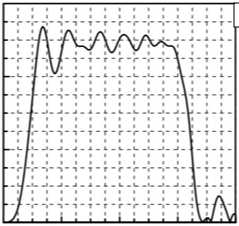
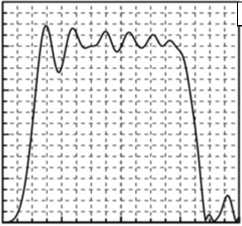
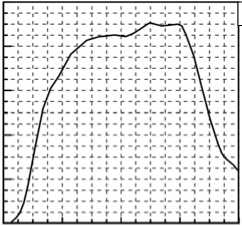
С использованием описанной выше трехмерной модели процесса были получены профили волн напряжения (сравнивались эффективные напряжения), прошедших через образец и распространяющихся далее по правому стержню. В случае малых скоростей ударника кривые, рассчитанные на основе параметров из таблицы, представлены на рисунке 5. Хорошо видно, что вычисленная амплитуда ударной волны почти в два раза превышает амплитуду прошедшей волны, измеренную в эксперименте. По всей видимости, это связано с не отвечающими действительности значениями расчетных параметров материала. В остальном, прежде всего по длительности импульса, профили неплохо соотносятся с экспериментальными. Следует также отметить сложность корректной обработки опытных данных и отсечения внешних шумов, что подробно обсуждается в работе [11]; на рисунке 5 эти кривые приведены уже в обработанном виде, когда отброшены также колебания, вызванные переотражением волн напряжения от боковой поверхности стержня.

а, МПа

а

О 40    80    120   160

t, мкс

а, МПа

О

О 40    80    120   160

/. мкс

ст, МПа

О 40    80    120 160

t, мкс

а, МПа

О

г

О 40    80    120   160

t, мкс

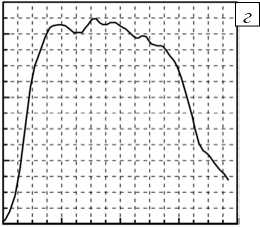
Рис. 5. Расчетные ( а , б ) и экспериментальные из [11] ( в , г ) профили ударных волн после прохождения образца при скоростях ударника, м/с: 4,51 ( а , в ) и 7,5 ( б , г )

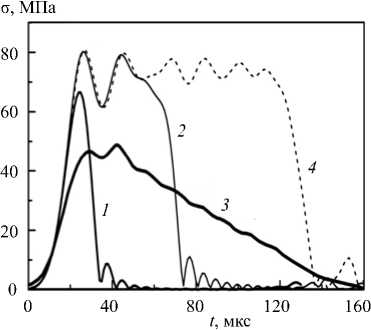
Рис. 6. Расчетные амплитуды ударных волн при скорости 13,51 м/с и различных пределах прочности влагонасыщенного материала, МПа: 20 (кривая 1 ); 30 ( 2 ); диаграммы напряжений по Мизесу из [11] ( 3 ) и для чисто упругого случая без разрушения образца ( 4 )

Кроме того, используемая модель процесса разрушения не дает плавного «растекания» профиля ударной волны, получаемого в экспериментах, а приводит к его резкому обрыву. Только после уменьшения ширины прошедшего через образец импульса до минимального значения (соответствующего амплитуде первого колебания на профиле падающей волны) расчетная амплитуда начинает уменьшаться (Рис. 6). Для сравнения на рисунке приведена экспериментальная кривая распределения напряжений для влагонасыщенного известняка (кривая 3 ) [11]. Всего профили, подобные представленным на рисунке 6, были рассчитаны для трех скоростей ударника и для каждой из них взято несколько значений предела прочности влагонасыщенного образца: от 10 до 40 МПа. Качественно полученные результаты для всех скоростей ударника оказались эквивалентными описанным выше при скорости 13,51 м/с.

Выявленное несоответствие расчетных кривых, полученных на основе одного набора параметров материала, картине разрушения, наблюдаемой в эксперименте, заставляет усомниться в точности выбранных параметров материала и побуждает к проведению серии расчетов в большом диапазоне возможных параметров динамической прочности материала.

• 5.    Изменение моды разрушения образца в зависимости от его прочности

Наиболее интересным результатом, полученным при моделировании процесса разрушения известняка с различной прочностью, стало обнаружение нескольких мод разрушения образца даже при одной и той же скорости ударника. Стоит отметить, что этот существенно трехмерный эффект связан с разным временем распространения по образцу падающих и отраженных от правой и боковых поверхностей образца волн напряжения. На рисунке 7 показаны три различных моды разрушения, реализующиеся при пределах прочности из ди апазона от 10 до 30 МПа и скор ости ударника 13,51 м/с. Показано напряжение по Мизесу: ст _м = JI ( ст 1 -ст ₂ ) 2 + ( о ₂ -о ₃ ) ² + ( ст , -о ₃ ) ² 1/ 2 , где ст i — главные напряжения.

Рис. 7. Моды разрушения влагонасыщенных образцов из материалов с различным пределом прочности, МПа: 10 ( а ), 20 ( б ) и 30 ( в ) при скорости ударника 13,51 м/с и параметрах модели из таблицы; нагружающий импульс приходит слева; удерживающие образец стержни (см. Рис. 2) убраны для наглядности

Рис. 8. Фотография разрушенного образца после его ударного нагружения на стержне Гопкинсона–Кольского [10] (третья мода разрушения)

Видно, что при малой прочности материала разрушение в образце начинается со стороны нагружаемой поверхности и происходит симметрично вдоль его боковой поверхности; самым последним разрушается материал в зоне вдоль центральной оси (первая мода). Такой вид разрушения, по-видимому, связан с действием отраженной от боковой поверхности мишени ударной волны при ее взаимодействии с падающей волной сжатия, что совершается быстрее, чем отражение волны от ее тыльной поверхности. В этом смысле аспектное отношение размеров образца также может влиять на моду его разрушения. Так, при той же скорости ударника в образце с более высокой прочностью (Рис. 7б) разрушение начинается с тыльной стороны, сердцевина же вдоль оси остается неповрежденной (вторая мода разрушения). При дальнейшем увеличении прочности материала разрушение вновь начинается с нагружаемой поверхности, но несколько позже по времени и уже однородно по поперечному сечению (не разрушенного вдоль оси материала не остается) на волне разгрузки ударного импульса (третья мода). На рисунке 8 представлена фотография разрушения, имевшего место в эксперименте [4, 5]. Очевидно, что разрушение образца из материала с наименьшим пределом прочности соответствует первой моде.

На рисунке 9 показано разрушение еще более прочных образцов (с пределом прочности 40 и 50 МПа) согласно четвертой моде. Основную роль здесь играет сходящаяся ударная волна, отраженная от правого торца образца. Разрушение начинается с нагружаемой стороны вблизи центральной части поперечного сечения образца и продолжается радиально к его краям и вдоль оси. Несимметричное разрушение образца здесь связанно с наличием пористости (см. Рис. 2), делающей материал неоднородным.

Таким образом, владение информацией о виде мод разрушения и наличие данных соответствующих экспериментальных наблюдений позволяют при трехмерном моделировании оценить диапазон изменения предела динамической прочности известняка интервалом порядка 10 МПа. Для рассматриваемых

Предел прочности, МПа:        40                                         40                                           50

Время, мс:              0,32                                           0,33                                             0,67

Рис. 9. Четвертая мода разрушения, соответствующая очень прочному образцу, для двух моментов времени ( а ) и ( б ) и волны разрушения в неразрушенном образце ( в )

экспериментов это в пределах от 10 до 20 МПа, что отвечает экспериментально измеренным значениям [4, 5] и не превышает величин ГОСТ для строительного известняка.

• 6.    Эффект задержки начала макроскопического разрушения образца

при разных амплитудах ударной волны

Кроме определения диапазона возможных значений предела динамической прочности материала трехмерное моделирование предоставляет также возможность исследовать интересный эффект «задержки» разрушения образца. Как отмечалось выше, в сухом и влагонасыщенном материале наблюдается различная скорость развития процессов динамического разрушения. Для описания этого эффекта может быть использован параметр инкубационного времени [5, 9, 10]. Очевидно, что при механизме разрушения в виде ориентированных трещин, на основе которого производится расчет, никакие инкубационные процессы не учитываются. При этом некоторые динамические эффекты «задержки» разрушения имеют существенно трехмерную природу и, накладываясь на более тонкие структурные особенности, скрадывают их. Так, в эксперименте традиционно предполагают, что разрушение материала происходит в момент времени, которому соответствует точка максимума кривой напряжения.

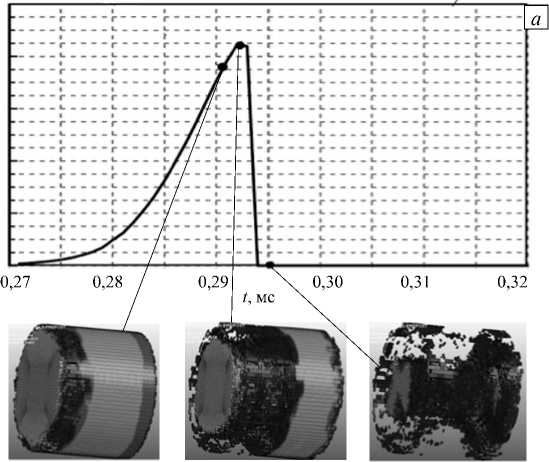
Интересно сравнить временны_́ е профили напряжения по Мизесу в образце с картинами его разрушения, отвечающими разным точкам этого профиля при различных модах разрушения, и определить соотносящиеся с ними моменты начала процесса разрушения. На рисунке 10 а , б приведены профили волн напряжения и картины разрушения хрупкого образца с прочностью 20 МПа и 30 МПа согласно первой моде разрушения при скорости ударника 17,5 м/с. В первом случае разрушение начинается за несколько микросекунд до момента достижения восходящей ветвью кривой своего максимума. Действительно макроскопическое разрушение большей части образца соразмеряется по длительности с областью под максимумом кривой, и сообразно с ней в последующем в образце наблюдается резкое падение напряжений.

с, ГПа

а

0,27        0,28

0,29

\ 0,30 t, мс \

0,31         0,32

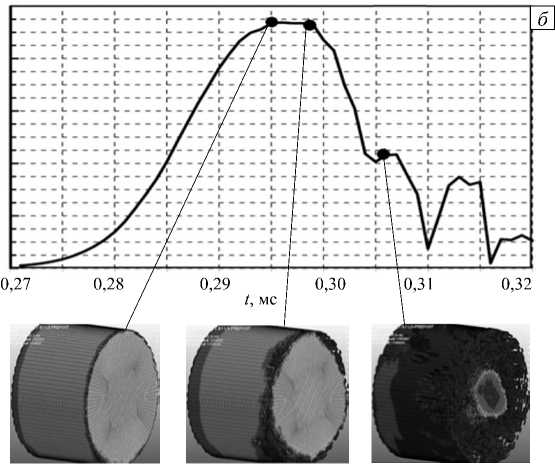
Рис. 10. Профиль волны напряжений и картины разрушения образца в различные моменты времени для первой (а) и второй (б) мод разрушения; прочность образцов равна, соответственно, 20 и 30 МПа с, ГПа

б

0,27        0.28

0,29

/, мс

0,30

0,31         0,32

Рис. 10. Продолжение

При большей прочности материала процесс разрушения начинается с правого торца образца, но фактическое разрушение наступает в момент времени, которому отвечает максимум кривой профиля волны напряжения и в основном заканчивается за время, соотносящееся с ее ниспадающей ветвью (Рис. 10). Максимум кривой растянут в плато продолжительностью порядка 10 мкс и еще столько же времени развивается макроскопическое объемное разрушение большей части образца. Для четвертой моды, когда разрушение начинается с нагружаемой поверхности в зоне вблизи оси образца и распространяется к его краям (Рис. 9), профиль волны напряжения в образце имеет более растянутый вид, разрушение начинается еще до момента достижения максимума, но значительно позднее начала «плато» на кривой максимальных напряжений. Ширина «плато» при этом доходит до 40 мкс и включает время t = 2 L^ р/ E ~ 20 мкс ( L , р , E см. в таблице), которое требуется волне, чтобы пройти через образец, и время, чтобы отразиться от правого торца и конически сойтись к нагружаемой поверхности образца, инициировав начало разрушения.

С уменьшением скорости ударника плато еще больше выравнивается, а времена процессов увеличиваются. На рисунке 11 показан пример моделирования разрушения образца без пор при скорости с, ГПа

о

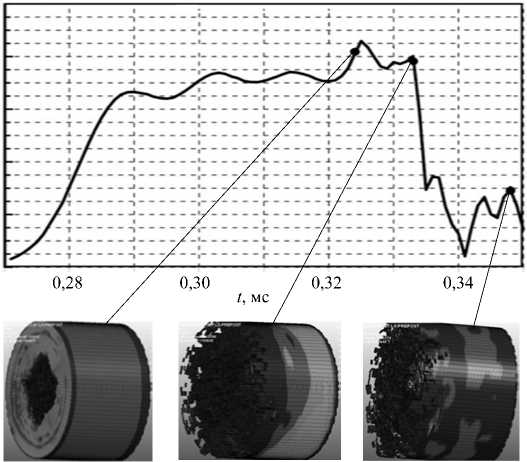
Рис. 11. Профиль волны напряжений и картины разрушения образца без пор в различные моменты времени для четвертой моды разрушения при скорости ударника 13,51 м/с и прочности образца 20 МПа

ударника 13,51 м/с и прочности образца 20 МПа. Видно, что в отсутствие пор разрушение становится фактически симметричным относительно оси образца. Практически весь процесс разрушения происходит на конечном участке «плато» кривой волны напряжений и длится порядка 10 мкс. После падения уровня напряжений, в отличие от двух предыдущих случаев, в течение 20 мкс образец не претерпевает никаких значительных изменений.

Таким образом, можно сделать заключение, что при динамических нагрузках критерий прочности, опирающийся на максимальное напряжение, справедлив лишь для достаточно хрупких материалов и нагрузок высокой амплитуды и не дает почти никакой содержательной информации для всех остальных случаев.

• 7.    Заключение

Реальная динамическая прочность образцов горных пород, в частности исследуемого здесь известняка, может в несколько раз отличаться от измеренной в экспериментах. Это создает большие сложности для численного моделирования соответствующих эксперименту процессов деформации и разрушения образцов и делает необходимым фактически произвольный подбор параметров прочности материала. При трехмерном моделировании, когда могут реализовываться различные моды разрушения материала, очень полезными оказываются данные о структуре материала до и после разрушения, чем часто пренебрегают при механических испытаниях. Именно благодаря трехмерному моделированию, совместному с экспериментальными исследованиями структуры нагруженных образцов, удается сузить диапазон возможных значений параметров материала. Кроме того, использование при этом достаточно простых пороговых критериев прочности материала позволяет отделить существенно трехмерные эффекты распространения и взаимодействия волн напряжения в материале от микроструктурных особенностей процесса разрушения, учитываемых через более сложные критерии с параметрами типа инкубационных времен.

В данной работе получен наиболее вероятный диапазон значений динамической прочности, отвечающий материалу, исследуемому в экспериментах [4, 5] — это 10–20 МПа при значении ГОСТ для испытуемого строительного известняка, превышающем 25 МПа. При этом значение предела динамической прочности, безусловно, не является характерной постоянной материала и зависит от скорости деформации, что было продемонстрировано, в частности, в работах [4, 5].

Проведенные исследования выявили четыре различных моды разрушения образца, сменяющих одна другую по мере увеличения прочности материала: первая — это разрушение боковой поверхности при сохранении целостности центральной зоны вдоль его оси; согласно второй моде разрушение начинается с правого торца образца и не затрагивает его центральную часть вдоль оси; третья — разрушение начинается с нагружаемого — левого — торца и равномерно движется по сечению образца; наконец, четвертая — разрушение начинается с нагружаемого торца, но не с краев, а вблизи центра, затем распространяется до краев и уже дальше однородно и постепенно охватывает весь объем материала образца вдоль оси. В четвертом случае разрушение вызывает уже отраженная от правого торца образца волна напряжения, конически сходящаяся в центральной части его левого торца.

При первых трех модах разрушение наступает практически одновременно с достижением импульсом напряжения максимума, но может начаться за несколько микросекунд до него и закончиться на ниспадающей ветви кривой волны напряжения. В последнем случае при повышенной прочности образца (когда наблюдается четвертая мода) кривая, характеризующая напряжения, оказывается мало информативной.

Эффект пористости был исследован только для случая крупных пор в образце. Вычисления продемонстрировали, что при относительно малой доле пор (около 5%) они оказывают незначительное влияние на механические свойства образца и вид профилей волн напряжения. Влагонасыщенные поры действуют фактически как твердые включения, а пустоты (поры с воздухом) в сухом образце достаточно сильно деформируются. При этом крупные поры приводят к асимметрии в разрушении образца, которая может быть заметна в эксперименте при неполном разрушении.

Работа выполнена при финансовой поддержке Российского научного фонда (грант 15-19-10007).