Проблема восприимчивости погранслойных течений и бифуркации периодических режимов

Основная задача исследования восприимчивости заключается в поиске, выборе, экспериментальном и теоретическом моделировании таких механизмов возбуждения колебаний, которые играют основную роль в формировании возмущенного течения и последующей его турбулизации [1]. К основным внешним факторам, которые вызывают возмущения, относятся шероховатость или геометрия поверхности, завихренность и турбулентность свободного потока (рис.1).

основной поток

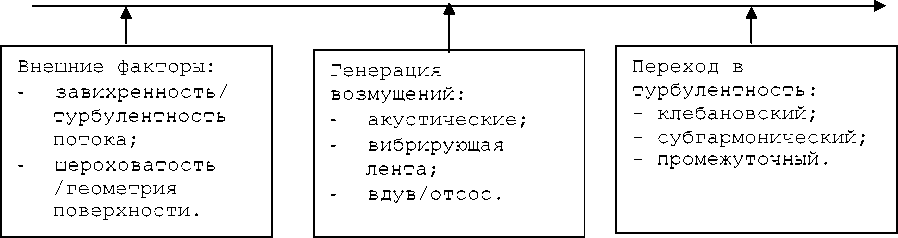
Рис.1. Механизмы восприимчивости

В зависимости от геометрии обтекаемого тела, размера шероховатостей, степени турбулентности или завихренности основного течения появляются возмущения и в дальнейшем может произойти их рост и переход в турбулентность. Кроме этого в экспериментах для генерации вынужденных возмущений применяются акустические методы, вибрирующая лента, вдув или отсос в поток, которые в зависимости от частоты или амплитуды могут перейти в турбулентное состояние.

В настоящее время развиваются следующие теоретические направления исследования механизма восприимчивости – параболизованные уравнения [2], прямое численное моделирование [3], возмущения в профиле параллельного пограничного слоя [4-5], взаимодействие возмущений [6-7]. В них рассчитываются коэффициенты восприимчивости возмущений от начальных данных, задающих внешние факторы, амплитуды и частоты возмущений.

В данной работе метод инвариантной конечномерной проекции уравнений Навье-Стокса, разработанный Б.Ю.Скобелевым [8], применяется для исследования периодических трехмерных возмущений в плоскопараллельном течении вязкой несжимаемой жидкости над плоской полубесконечной пластиной. При этом нелинейная начально-краевая задача для возмущений основного течения сводится к конечномерной рекуррентной системе линейных краевых задач для обыкновенных дифференциальных уравнений [9]. Предложенный универсальный алгоритм позволяет численно находить амплитудные поверхности устойчивых и неустойчивых режимов и точки тангенциальных бифуркаций периодических режимов для произвольных частот и чисел Рейнольдса.

Метод инвариантной проекции

Суть метода инвариантной конечномерной проекции состоит в том, что решение уравнений Навье-Стокса для возмущений:

^u + ( u ∇ ) u + Lu = 0,

∂ t

Lu = (u ∇) + (u∇)u - ∇q -   ∆u,

0           0        Re div u = 0

ищется в виде:

u = v2n + u⊥, где v2n – линейная функция m собственных функций оператора L, а ортогональное дополнение u⊥ ищется в виде функции от v2n u⊥ =g(v2n).

Условие того, что решение принадлежит инвариантному многообразию уравнений Навье-Стокса однозначно определяет вид функции g ( v _{2 n} ) . Существенным достоинством метода инвариантной проекции является то, что он гарантирует правильное описание асимптотического поведения решений (т.е. при t → ∞ ) и учитывает дискретный и непрерывные спектры возмущений.

В работе рассматривались моногармонические решения, периодические по продольной координате с волновым числом α и по поперечной координате с волновым числом β .

В соответствии с теорией инвариантной конечномерной проекции решение уравнения для функции тока представлялось в следующем виде:

∞s ф (x, y, z, t) = 2 A(t) Re [ f (y) ё(ax+et)) ] + £ As(t) £ gsk (y) e(az+e-e(t», s=1       k=-s где A(t) и θ(t) – амплитуда и фаза возмущения, δ – символ Кронекера, f(у) – собственная функция задачи Орра-Зоммерфельда для течения Блазиуса, а gsk удовлетворяют следующей рекуррентной системе уравнений:

ik a _ ( №. - U ) A _k + DU ^] g sk - ^⁽ A k ⁾² g sk = -5 k !⁽ b s - i + ic s — ₁ ⁾ A ₁ f - 5 k , — j *

^R                                          (1)

• * ⁽ b s - 1 — ic s - 1^{) A} 1 f — ^ik £ c q ^A k g pk ^{- i a} £ £ [ lgqiD ^A j g pj ^- jDg ql ^A l g pj ] , q + p = s                   q + p = s l + j = k

где D = ^d , ∆ = D ² - ( k α ɶ ) ² , α ɶ ² = α ² + β ² , U(y) – профиль невозмущенного ламинарного потока, f dy ^k

– сопряженная к собственной функции задачи Орра-Зоммерфельда, σ = σ _i + i σ _r – собственное число задачи Орра-Зоммерфельда.

Из условий прилипания на пластине и затухания возмущений на бесконечности ставятся следующие граничные условия:

g sk (0) = Dg sk (0) = 0, g sk ( ∞ ) = Dg sk ( ∞ ).

Коэффициенты b_{s - 1,} c_{s - 1} определяются из условий ортогональности и нормировки:

∞∞

∫ f ( y ) ∆ ₁ q_{s 1}( y ) dy = 0, ∆ ₁ = D ² - α ɶ ² , b_{s - 1} + ic_{s - 1} = ∫ f ^* F_{s 1} dy , 00

где f*(y) – решение уравнения, сопряженного к уравнению Орра-Зоммерфельда.

Результаты расчетов и их анализ

В работе проводился численный расчет приближенных уравнений для амплитуд периодических режимов

∞

γ + ∑ b 2 n Α ^{2 n} = 0. n = 1

при N =2,3,4,5, где γ = ασ _i – линейный коэффициент нарастания.

При численном интегрировании системы (1) граничные условия на бесконечности заменялись граничными условиями на интервале (0,L), L>>1. Затем преобразованием y = L y , 0 ≤ y ≤ L , 0 ≤ y ≤ 1 задача сводится к интегрированию на интервале (0,1). Вычисление присутствующих в правой части собственных функций задачи Орра-Зоммерфельда, а также решение системы (1) проводилось методом ортогональной прогонки [10] на неравномерной разностной сетке.

В результате вычислений выявилась следующая картина (рис.2-3). При малых значениях волнового числа α, соответствующих нижней ветви линейной нейтральной кривой, от течения Блазиуса ответвляется устойчивый периодический режим. При некотором α=α 2 передняя складка амплитудной поверхности из нефизической области отрицательных значений квадратов амплитуд выходит в область положительных значений и происходит смена закритической бифуркации докритической (α=α 3) . С увеличением числа Рейнольдса амплитуда этого режима нарастает, затем уменьшается и далее этот режим исчезает в результате слияния с неустойчивым режимом, ответвляющимся от верхней ветви линейной нейтральной кривой. Точки слияния этих режимов называются точками тангенциальной бифуркации [11], соответствующие точкам складки в теории катастроф [12]. Далее с увеличением α амплитудная поверхность периодических решений отрывается от линейной нейтральной кривой (α=α 4) и при некотором значении α периодические решения исчезают.

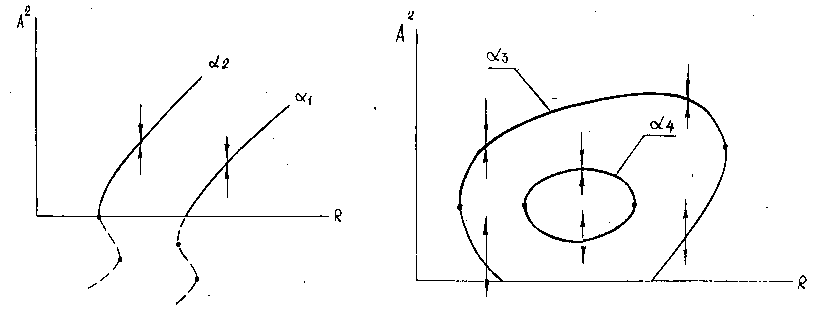
Рис.2                                             Рис.3

На рисунке 4 приведен срез амплитудной поверхности при α=0.206906, из которого видно, что при определенных начальных амплитудах периодические возмущения могут перейти либо в устойчивый периодический режим, либо в неустойчивый. На рисунке 5 приведены линейная нейтральная кривая (сплошная линия) и точки складок, или, что то же самое, точки тангенциальной бифуркации трехмерных режимов. Внутри нейтральной кривой возмущения нарастают, а вне – затухают.

В настоящее время экспериментально обнаружены три типа перехода. Первый был обнаружен в классической работе Клебанова и др. [13]. Он характеризуется быстрым нарастанием возмущений, высокочастотными всплесками и последующим образованием турбулентных пятен. Другой тип перехода был обнаружен в экспериментах Качанова, Козлова, Левченко [14]. Он характерен нарастанием высших гармоник двумерной волны Толлмина-Шлихтинга с последующим ростом трехмерной субгармоники. В экспериментах Козлова, Левченко, Сарика [15] наблюдался третий тип перехода – промежуточный между первыми двумя типами.

График амплитуды при «=0.206906

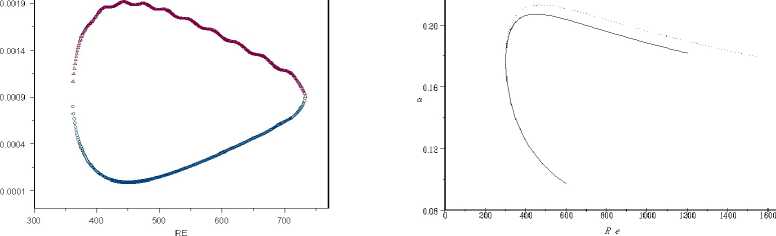
Рис.4 Рис.5

Для объяснения этих явлений в настоящее время существуют две основные теоретические модели. Первая была разработана Крейком [7] и по сути является обобщением метода Стюарта-Ватсона на случай взаимодействия трех резонансных волн. Другая модель – модель вторичной неустойчивости [6] – исследует устойчивость двумерных нелинейных волн относительно трехмерных линейных возмущений. Полученные с помощью этих моделей области быстрого роста трехмерных возмущений достаточно хорошо совпадают с экспериментальными результатами по наблюдению первых стохастических пульсаций. Но эти работы не объясняют причину появления стохастичности.

Как известно, в экспериментах по генерации ламинарно-турбулентного перехода с помощью вибрирующей ленточки клебановский тип перехода наблюдается только при относительно больших начальных амплитудах возмущения и характеризуется резким ростом возмущений. Таким образом клебановский тип перехода можно связать с передней верхней частью амплитудной поверхности, причем амплитуда соответствующего возмущения должна быть не меньше амплитуды периодического решения в передней точке тангенциальной бифуркации.

Если начальная амплитуда меньше критической клебановской, то возможен другой тип перехода, который можно соотнести с промежуточным типом, наблюдавшимся в эксперименте. Этот тип перехода связан с тем, что в результате нарастания возмущения становятся трехмерными и внутри нелинейной нейтральной поверхности для плоских возмущений их амплитуда может стать равной амплитуде точки тангенциальной бифуркации для трехмерных возмущений (β≠0).

И, наконец, при субгармоническом типе перехода в эксперименте наблюдается рост высших гармоник начальной двумерной волны Толлмина-Шлихтинга. Причем начальные амплитуды возмущений, вызывающих этот тип перехода, достаточно малы, и начальные возмущения действительно являются двумерными. Поэтому естественно связать субгармонический тип перехода с задней точкой тангенциальной бифуркации в окрестности верхней ветви линейной нейтральной кривой.

Таким образом, каждому типу перехода соответствует точка тангенциальной бифуркации периодических режимов (трехмерные или двумерные). Из теории динамических систем [16] следует, что в окрестности точки тангенциальной бифуркации возникает явление перемежаемости (т.е. чередование во времени ламинарного и турбулентного режимов). Причем длительность турбулентных режимов зависит от "расстояния" до точки тангенциальной бифуркации. Наблюдающаяся в экспериментах картина дает качественное подтверждение высказанным на основе проведенных расчетов предположениям.