Проблемы и модели информационного процесса при решении тактико-специальных задач летным составом в условиях информационно-психологического воздействия

Актуальность выбранной темы определяется особенностью подготовки штурманов многоместных самолетов ВВС, их функциональной готовностью по анализу получаемой информации, оценке ее и принятию решения на выполнение основных задач, связанных с эксплуатацией штатного оборудования (радиоэлектронной борьбы, разведки, навигации и применения средств поражения).

Рассматривая подготовку как основную составляющую профессионального становления штурманов следует отметить, что в настоящее время целевой программы обучения штурманов в условиях информационно-психологического воздействия в ВВС не существует. В связи с этим предлагается рассмотреть математическое обоснование информационного процесса для подготовки штурманов ВВС.

Анализируя группы средств получения информации и зная основные функциональные обязанности по должностям, которые могут замещать офицеры с образованием штурман-инженер, необходимо задаться вопросом: какой процент (или с какой вероятностью) информации необходим для принятия грамотного решения на подготовку и ведение активных действий [ 1 ] .

Например: начальник службы радиоэлектронной борьбы (РЭБ) в своей деятельности концентрирует всю информацию, получаемую от основных средств навигации, применения средств поражения, разведки и РЭБ. При этом, согласно основным руководящим документам по планированию мероприятий РЭБ, он должен оценить не менее восемнадцати позиций для принятия решения на активные действия. Необходимо отметить, что техническое оснащение рабочих мест приема и передачи информации различное, сам процесс приема и передачи подвержен воздействию помех различного вида и назначения, а также много других факторов в итоге оказывают влияние на эффективность использования информации. По вышеперечисленным вопросам необходимо вести подготовку на всех этапах активной деятельности. В условиях непосредственной подготовки и ведения действий информационное воздействие приобретает значение вида подготовки, при этом необходимо учитывать информацию для воздействия на «противника» (рис.1). Результатом такого процесса может быть: искажение информации (полное или частичное); подавление линий приема и передачи информации (полное или частичное); дезинформация.

Искажение информации предусматривает, что на пункте приема она приобретает вид, который не позволяет использовать ее по назначению (полное искажение) либо информация неоднозначна (частичное).

Подавление означает, что информацию невозможно распознать и она непригодна к использованию (полное подавление) или от переданного сообщения остался минимум данных, который также невозможно использовать в полном объеме.

Дезинформация предусматривает возможность на различных этапах приема и передачи информации введения сведений, которые изменяют значение передаваемого сообщения.

Для математического описания рис.1. воспользуемся теорией нелинейных систем, решающих задачи теории информации с использованием метода определения оптимальных систем [ 2 ] . На вход нелинейной системы поступает сигнал (информация J 0 ), представляющий функцию времени t и n -ое количество информационных параметров J 1… J n ,

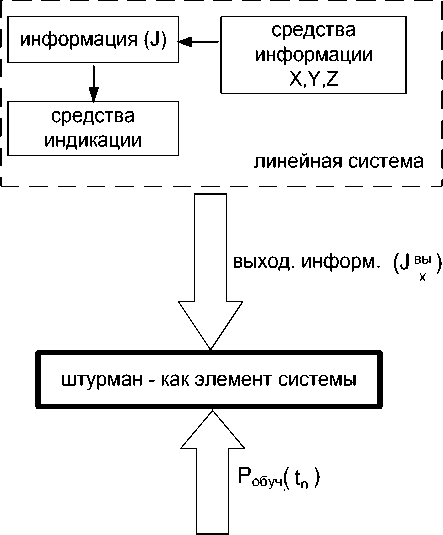
Вход. информ. Jo

J o = J

нелинейная система J вы = J o + S(t o ) х	T вып .б.з. (Р обуч . t n ) информация                   n  n необходимая    для           вых   ^   °^ ° ’ обуч’ выполнения б.з.(J вы ) (t 5 )        i J = J ma + J* информация после       *    x J -искаженная информация воздействия (J) ( ) (t4) J ma – максимум
-   внутреннее   (психологич. готовность  к выполнению б.з., совместимость экипажа) -    внешние (опер. обстановка) -    технические (помехи)	иxнформации без искажения Воздействие T       уточнение         (t ) предложений         3 штурман        T предложени   (t2) информация (J ) T анализа и обработки (t 1 ) средства получения информации      T получ. информ. (t 0 )

Рис. 1. Алгоритм информационного анализа системы.

Применительно к алгоритму информационного анализа (рис.1) зададимся следующими условиями:

• 1.     Прохождение информация осуществляется через основные 6 этапов, которым

соответствуют временные интервалы:

• -    этап 1 – t 0 – время получения информации;

• -    этап 2 – t 1 – время анализа и обработки информации;

• -    этап 3 – t 2 – время на оценку информации согласно уровню подготовки должностного лица (штурмана);

• -    этап 4 – t 3 – время на уточнение предложений в условиях воздействия на штурмана таких факторов, как технические, внешние, внутренние и психологическая совместимость экипажа;

• -    этап 5 – t 4 – время на анализ и обработку информации после воздействий, количественная оценка искаженной информации;

• -    этап 6 – t 5 – время на оценку информации, необходимой для принятия решения на выполнение полета.

• 2.    J 0 – начальная информация, которой располагает штурман до начала ведения активных действий.

• 3.    J 1…n – информация, поступающая поэтапно в ходе активных действий.

• 4.    P 0 – уровень подготовки штурмана на момент начала активных действий.

• 5 .    P обуч – уровень подготовки штурмана, достигаемый в ходе ведения активных действий.

Алгоритм информационного анализа (рис.1) с учетом принятых условий можно представить графически (рис.2). Поэтапное время определяется конкретной обстановкой, техническими средствами информации, уровнем подготовки должностного лица. Необходимым условием данного процесса должно быть постоянное накопление информации в реальном масштабе времени.

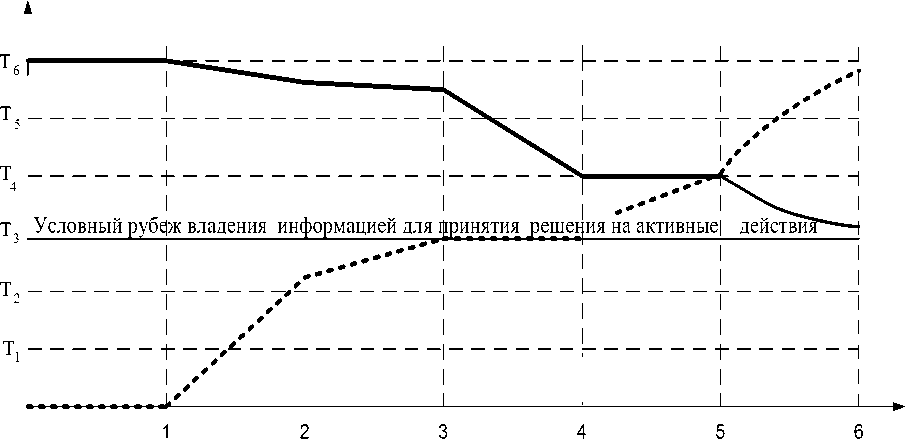
владение информацией о противнике нами владение информацией противником о нас

Рис. 2. Соотношение поэтапного получения, анализа, обработки и применения информации между своими силами (средствами) и силами (средствами)условного противника

J ( t ) = f ( t , J 1... J n ) или

n

J ( t ) = f t , E J

V    i = 1     7

На выходе необходимо получить информацию после всех возможных воздействий. Решением данной задачи является сигнал J(t), который максимально точно воспроизводит ин- формацию на выходе ивых(1), что является частным случаем основной задачи теории оптимальности для информации:

J вых (t) = J o (t) +S(t)                                     (2)

где: J₀(t) - полезный сигнал; S(t) - помеховый сигнал;

при использовании различных вероятностных критериев точности, например:

M[E(J, J)] = min                               (3)

где: E(J, J) - функция выходного сигнала J_вых(t) и реального сигнала с учетом всех возможных воздействий J .

С целью определения числовых характеристик информационного процесса используем ряд Маклорена [2], при этом считаем, что функция E(J, J) разлагается в ряд по переменным J 1_ J_n . В соответствии с допущениями, найдем приближенно:

q    nnn

J(t )= Ao (t ) + £ J. Т £ £ ."£ At 1,12... ,п (t)A (t1, t 2...t. ,J1, J2-.-Jn )

k=1      k tx =1  t2 =1 t„ =1

Формула (4) дает приближенное представление всего информационного процесса и его конкретных значений в виде номиналов q -ой степени от нескольких переменных. Функции A₀(t) и A_ti,t₂ ...\ (t) можно рассматривать как коэффициенты, посредством которых информационные процессы апроксимируются указанными номиналами в диапазоне возможного количества информации. Зная коэффициенты и количество информации в конкретное время подготовки и ведения боевых действий, можно найти числовые характеристики процесса J(t), рассчитать математическое ожидание m_J и дисперсию D_J :

• m , = A o ( t ) + £ 1 £ t-£A , J -J. ( t ) ■ Dj.. J ,-J.                           (5)

k = 1 k • 1 1 = 1 1 2 = 1    t . = 1

где:                        D j . , j . ..J . = M [ J 1 , J . ... J . ]

смешанные центральные моменты информационных величин или D j i , j . ... j . = M [ J , ] = D [ J j ]

Дисперсия:

^djj ^{( t} ) = ° , ^{( t} ) = ^{M [ J 2 ( t )]-} m J ^{( t} )

где: aJ(t) - среднее квадратическое отклонение информационного процесса. Используя выражение:

M [ J ² ( t ) ] = M

q   nn   n lAo (t )+£ 1 ZZ-Z A j .. j k =1 k • 11 =1 12 = '   t„ =1

I

^{( t} )M A > ⁽ t ⁾⁺ £- £ £ ... £ a j i , j 2 ... j . ^{( t} ) ^

i            j=i j • j.=i j2=i и соотношение (5), получим окончательное выражение для дисперсии и среднего квадратического отклонения:

qq    nn  nn nn d (t )=^ (t )=££     ££■■.£££.■■ £ , 2..,. (t)-At,, 12...t. (t) d,„,    „,.-[«j (t)-A> (t )]2

k=1 J=1 k • J! t. =112 =1 t. =1J. =1J 2 =1

Формулы получены в результате представления соотношения (4), что позволяет вычислить корреляционную функцию, начальные и центральные моменты информационного процесса более высоких порядков.

На основании выше сказанного и применив разложение рядов Маклорена, для шестиэтапного прохождения информации можно рассчитать коэффициент А₆ , т.е. J_вых :

f¹ (t ) = a, + 2 at + 3 at ² + 4 a«t ³ + 5 a J ⁴ + 6 at ⁵

12   3    4    56

f II ( t ) = 2 a + 2 ■ 3at + 3 • 4 a.t ² + 4 • 5 aX ³ + 5 • 6 aX ⁴

23   4    56

f11 (t) = 2 • 3 a3 + 2 • 3 • 4 a4t + 3 • 4 • 5 a5t2 + 4 • 5 • 6 a6t3

f^IV ( t ) = 2 • 3 • 4 a ₄ + 2 • 3 • 4 • 5 a₅t + 3 • 4 • 5 • 6 a₆t ²

f (t )= 2 • 3 • 4 • 5 a5 + 2 • 3 • 4 • 5 • 6 a6t fV (t ) = 2 • 3 • 4 • 5 • 6 a6 = 720a6

На основании коэффициент для шестиэтапной информационной системы можно найти следующим образом:

VI

a 6 =     = 1

n !

Таким образом, для рассмотренного шестиэтапного алгоритма информация на входе в систему равна информации на выходе из системы, что свидетельствует о факте отсутствия каких-либо воздействий на информацию (свойство линейной системы).

Для нелинейной системы необходимо определить весовой коэффициент К J , который будет определять процентную (вероятностную) потерю (искажение) информации при переходах от этапа к этапу. Если рассматривать условие, что информация равномерно теряется (искажается) на каждом переходе, то K J ® 0,20. По алгоритму информационного анализа системы это неверно, ввиду особенностей каждого этапа и самой информации, присущей этим этапам, поэтому необходимо рассмотреть вопрос доверительных интервалов. Для расчета доверительных интервалов воспользуемся теорией статистики [1]:

Результаты расчетов:

М = 4,44 SS = 7356,8 S м = 4,4 S =19,68

где: М – среднее арифметическое для группы из 20 человек с соответствующим уровнем подготовки; t – показатель по критерию Стьюдента; S M – статистическая ошибка, которая является мерой точности расчетов; SS – показатели вариации; S – стандартные отклонения.

Для рассматриваемого шестиэтапного информационного процесса, который охватывает 20 человек руководящего состава (начальники основных авиационных служб), необходимо ответить на основной вопрос: с какой min вероятностью (в каком доверительном интервале) возможно использование оперативной информации для принятия грамотного решения на выполнение полетного задания? Отвечая на этот вопрос, используем формулу для расчета точности оценки:

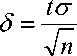
где: ст - среднее квадратическое отклонение

По данным расчетам построен график доверительных интервалов.

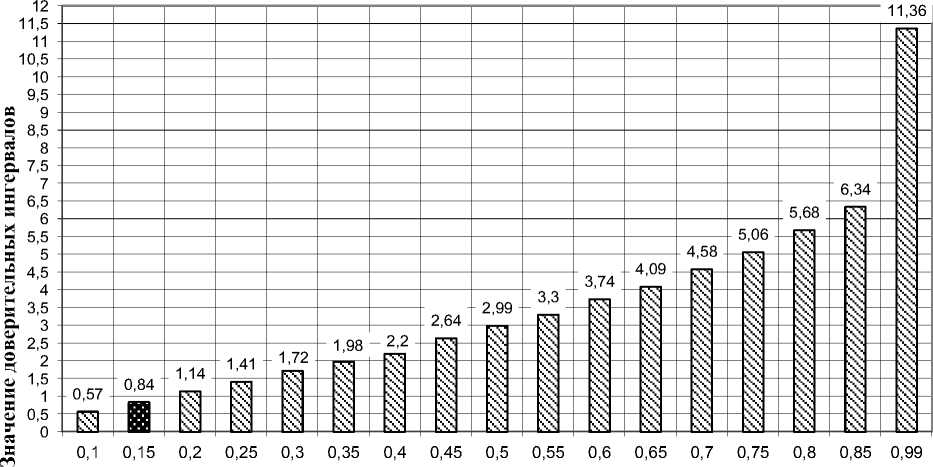
Вероятности

Рис. 3. График доверительных интервалов

Анализируя рис.3 и рис.2 можно отметить, что доверительный интервал, равный 4,4 ± 0,84 = 3,6 + > 5,0 при Р > 0,15, соответствует условной информационной границе принятия ре- 125 - шения на активные действия и уровню подготовки штурмана не ниже среднего балла 3,6, что является оценкой «хорошо» и означает, что из 18 вышеупомянутых позиций начальнику службы достаточно знать не менее 3 пунктов для принятия грамотного эффективного решения. Полученные результаты, позволяют решить и обратную задачу: при потере какого количества информации принятие решения на активные действия невозможно:

Р потери = 1 - 0,15 = 0,85 (14)

Таким образом, предложенный подход является инструментальным средством, позволяющим летному составу анализировать и моделировать варианты решения тактикоспециальных задач.