Проблемы обеспечения геометрической корректности компьютерных CAD моделей в системе NX

использования CAE программ для деталей и сборочных единиц, CAD модели которых созданы с неявными ошибками построения, либо подлинником конструкторской документации которых является проекционный чертеж или физическая модель [5, 6]. В связи с тем, что CAD/CAE конвертеры современных CAE систем осуществляют детальную проверку топологической корректности геометрии импортируемых CAD моделей, но не имеют эффективных средств устранения погрешностей построения, необходимо обеспечить корректное моделирование нелинейных поверхностей, образующих геометрию деталей, в среде создания CAD модели. Ошибки (на первый взгляд не имеющие принципиального значения) в части обеспечения непрерывности поверхностей, образующих геометрию детали, приводит к возникновению пустых, взаимопроникающих элементов при конечно-элементном разбиении в CAE системах, и, в конечном итоге, к созданию моделей, непригодных для дальнейшего моделирования. Кроме того, создаваемые на этапе CAD моделирования линии и точки стыков независимо формируемых поверхностей при конечноэлементном разбиении образуют области сгущения конечных элементов, резко и необоснованно увеличивая число степеней свободы и, как следствие, вычислительную трудоемкость модели (см. рис. 1).

Высокая эффективность сквозных CAD/CAE технологий, большая трудоемкость работ по устранению перечисленных погрешностей CAD моделей актуализировали усилия ведущих разработчиков программного обеспечения по созданию специализированных программных пакетов как, например, CADdoctor разработки фирмы Elysium [7]. В представленной работе рассмотрены этапы анализа и устранения ошибок топологической корректности CAD модели, построенной в среде NX, на примере композитной конструкции, имеющей геометрию типа пологой открытой оболочки, полимеризуемой в открытой форме. Результаты выполненных корректировок иллюстрируются реконструированными CAD моделями и конечно-элементными разбиениями самой формуемой детали и технологической оснастки, выполненными в CAE среде Comsol Multiphysics.

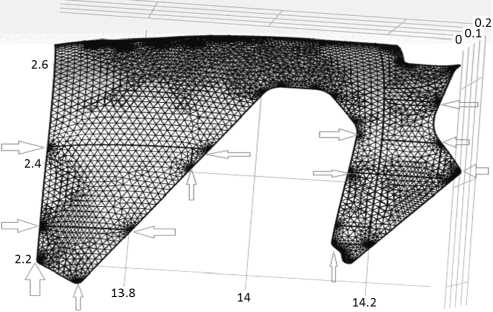
Рис. 1. Визуализация конфликтов построения конечно-элементной сетки в CAE системе, вызванных ошибками геометрических построений в среде CAD

Анализ корректности геометрических построений исходной CAD модели. Выявление и количественную оценку ошибок построений наиболее удобно производить в программной среде, использованной при построении CAD модели детали. В рассматриваемом ниже случае это система Siemens NX 8.5. Представленные ниже ошибки обусловлены примененной при построениях технологией формирования поверхности детали сложной формы из отдельных сегментов, которые могли задаваться с помощью системы точек по результатам сканирования поверхностей координатно-измерительной машиной (КИМ); их количественные значения определяются настройками измерений, обработки данных и сохранения результатов. С учетом того, что рассматриваемая исходная деталь имеет постоянную толщину, и ее построение выполнялось обрезкой по заданному контуру с последующим утолщением «теории», рассмотрим этапы анализа наружной и внутренней поверхности для двух сопрягаемых сегментов поверхности (см. рис. 2, 3).

Анализ внутренней поверхности с помощью инструментов «Анализ-форма-непрерыв-ность поверхности» показывает, что сшивка двух сопрягаемых сегментов S1I и S2I осуществлялась только по координате. Требования к непрерывности сшивки поверхностей по первой, второй и третей производным не предъявлялись. На рис. 2а выделены два сопрягаемых сегмента поверхностей, а на рис. 2б - 2д – графики распределений скачков координаты, первой, второй и третьей производной поверхностей сшиваемых сегментов по нормали к линии сшивки.

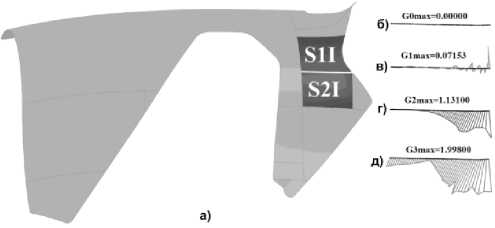
Рис. 2. Анализ непрерывности сшивки двух сегментов (S1I и S2I) внутренней поверхности вдоль периметра кривой сшивки длиной – 96.264 мм (Пояснения в тексте)

В результате анализа внешних поверхностей установлено, что сшивка двух сегментов внешней поверхности S1E и S2E, соответствующих сегментам S1I и S2I, не выполнена ни по координате, ни по производным. На рис. 3а выделены два сегмента поверхностей, а на рис. 3б - 3д – графики распределений скачков координаты, первой, второй и третьей производной поверхностей сшиваемых сегментов по нормали к линии сшивки.

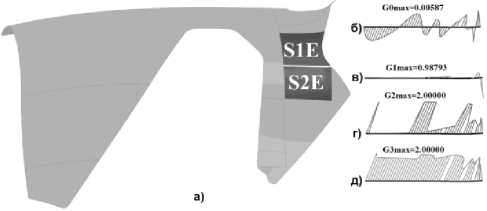
Рис. 3. Анализ непрерывности сшивки двух сегментов (S1E и S2E) внешней поверхности вдоль периметра кривой сшивки длиной -96.2002 мм (Пояснения в тексте)

Выполненный анализ показывает, что автор модели в качестве теории использовал внутренние сегменты поверхности детали. Это утверждение связано с особенностью CAD программ формировать объем листового материала приданием толщины поверхности, ограниченной контуром. Придание толщины осуществляется инструментом «Утолщение», создающим границы объемного листового тела смещением всех точек исходной поверхности на заданную величину, в направлении, нормальном к исходной поверхности в каждой точке. Эту особенность можно проиллюстрировать с помощью инструмента «Кривая смещения», работающему по тому же принципу, но с кривыми. На рис. 4 стыкуемые кривые 1 и 2 имеют одну общую точку, но требование к непрерывности касательных обеих кривых в этой точке не выполнено. Кривые 1-1 и 2-1 получены путем смещения кривых 1 и 2, соответственно, вдоль внешних нормалей к каждой из кривых на одинаковую величину, а кривые 1-2 и 2-2 - в противоположном направлении. Результат построения, приведенного на рис. 4, показывает, что невыполнение требования к непрерывности касательной к двум кривым в общей точке приводит к разрыву между смещенными кривыми 1-1 и 2-1 и пересечению кривых 1-2 и 2-2.

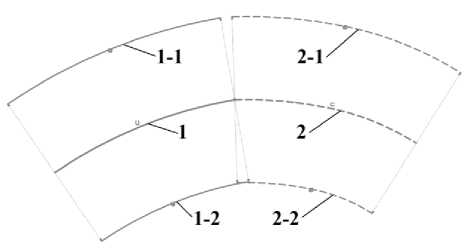
Рис. 4. Особенности «смещения» кривых в CAD

Аналогичная ситуация возникает и при смещении поверхностей, что приводит к возникновению незаметных для конструктора ошибок построения поверхностей. Важно отметить, что в случаях, когда поверхность модели детали построена как поверхность смещения, то при утолщении такой поверхности уже требуется гарантировать выполнение требования непрерывности сшивки по второй производной, а в случае смещения уже смещенной поверхности – выполнение требования непрерывности сшивки по третьей производной.

Современные CAD программы предоставляют широкую гамму инструментов, позволяющих редактировать как отдельные поверхности за счет расположения вершин (полюсов) характеристического многогранника или изменения степени управляющих полиномов и количества полюсов (см. рис. 5), так и осуществлять сшивку сопрягаемых поверхностей за счет замены ребра одной из сшиваемых поверхностей на ребро другой с заданием требований к непрерывности. На рис. 5 показана возможность CAD системы для одной из сопрягаемых поверхности задавать различные количества вершин управляющего многоугольника. Однако в рассматриваемом примере по результатам работы КИМ сохранены только разорванные ассоциативные копии поверхностей без математического описания их родителей.

Такая ситуация весьма характерна и часто встречается в практике серийных и разрабатывающих КБ, когда никаких работ по моделированию и оптимизации проектируемого изделия не предполагается, а создаваемая CAD модель используется для выпуска бумажных чертежей или управляющих программ ЧПУ.

Последовательность построений новой CAD модели взамен исходной. В рассматриваемом случае потребовалось заменить исходную многосегментную поверхность «теории» на единую поверхность. Так как новая теория будет использоваться не только для построения модели детали, но и для построения модели оснастки, которая превосходит по размерам деталь, потребуется ее расширить за границы детали. При этом сама поверхность должна быть описана кривыми второго порядка, а продолжение за границы детали предпочтительно должно сохранять кривизну поверхности на границе или быть линейной, соблюдая требования к непрерывности координаты и первой производной.

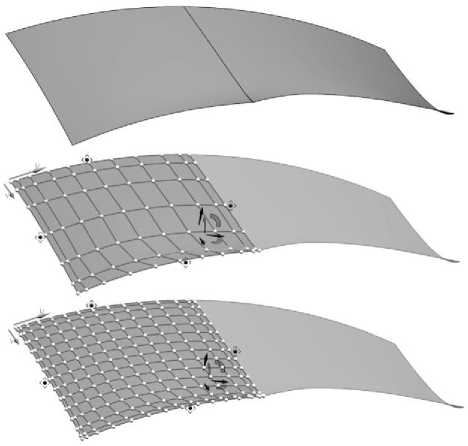
Рис. 5. Редактирование поверхности путем изменения расположения и количества вершин характеристического многогранника

Для решения поставленной задачи в исходной модели детали были:

• -    созданы ассоциативные копии кривых границ детали на внутренних поверхностях; удалены, инструментами синхронного моделирования,

• -    выполнены скругления на торцах листового тела (что необходимо для обеспечения возможности построения новых границ недостающих поверхностей);

• -    созданы ассоциативные копии внутренних поверхностей.

На основе ассоциативных копий сегментов поверхности были созданы поверхности, расширяющие исходные, заполняя пустоты между ними.

В рамках этой задачи потребовалось не только использовать различные инструменты создания поверхностей с учетом требований к непрерывности касательных и кривизны к соседним поверхностям, но и построить новые границы недостающих поверхностей, используя инструменты создания кривых по существующим кривым. Результаты описанных преобразований представлены на рис. 6.

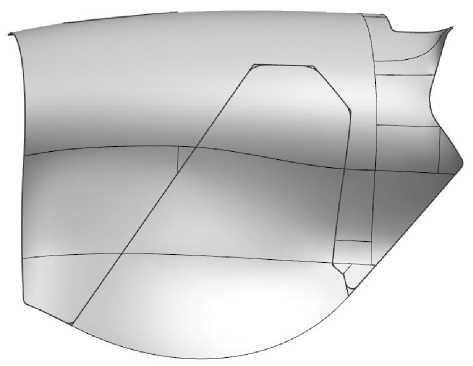
Рис. 6. Поверхности, расширяющие поверхности ассоциативной копии

Принимая во внимание, что часть поверхностей являются ассоциативными копиями с исходных и, следовательно, наследуют ошибки их сопряжения, а редактирование родителей ассоциативных копий не представляется возможным, были построены кривые второго порядка в продольном и поперечном направлениях. Принимая во внимание наличие ошибок сшивки поверхностей, все они были рассечены ортогональной системой плоскостей, а полученные кривые сечения каждой плоскостью сопрягаемых поверхностей заменялись на единую кривую второго порядка с расширением на начале и конце кривой.

В некоторых случаях расширение кривой было невозможно, по таким причинам как самопересечения кривой или ярко выраженное отклонение от линейности, вызванное интенсивностью изменения кривизны у кромки в направлении продления кривой. Это затруднило бы в дальнейшем проектирование оснастки, и не оказало бы никакого влияния на точность построения. Для таких случаев расширение кривой осуществлялось построением прямых отрезков из конца кривой касательно к ней. Ряд кривых, расположенных за пределами исходных поверхностей, приходилось достраивать по отдельным фрагментам или, учитывая интенсивность изменения кривизны поверхности, путем дополнительных построений.

Результаты корректировки исходной CAD модели. Простое построение новой по- верхности по сетке кривых позволило создать новую «теорию», близкую по геометрии исходной. Новая «теория», представленная на рис. 8, позволяет создать модели, как детали, так и оснастки, пригодные для дальнейшего моделирования в CAE программе.

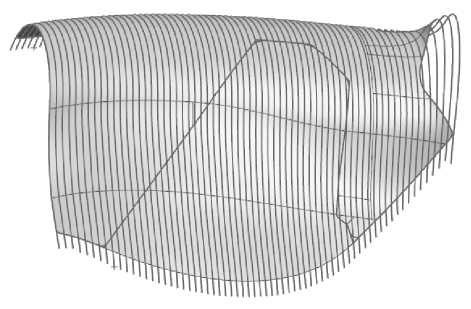
Рис. 7. Результат построения сетки кривых в поперечном направлении, продленных за пределы исходной поверхности

Однако созданная новая «теория» будет геометрически отличаться от исходной. Эти отличия могут быть оценены величиной нормы отклонений или непосредственным анализом отклонений точек поверхностей. Такой анализ возможен только в пределах геометрии исходной детали. Величина полученных отклонений, представленных на рис. 9, отображена в миллиметрах и может быть уменьшена за счет увеличения плотности кривых второго порядка, задающих вновь построенную поверхность.

Результатами описанных действий стали топологически корректные модели детали и оснастки (см. рис. 10), используемой для ее формообразования, пригодные для выполнения конечно-элементного анализа и имеющие отклонения от геометрии исходной модели на порядок меньше чем допуск на изготовление. Следует отметить, что эти отклонения неизбежны и без корректировки модели, так как реальная деталь не может иметь сегментированную поверхность с наличием разрывов между отдельными сегментами.

Конечноэлементное разбиение геометрии совмещенных детали и формообразующей оснастки представлено на рис. 10б, 10в. Простое качественное сопоставление разбиений, представленных на рис. 1 и рис. 10, показывает, что отредактированная геометрия CAD модели свободна от необоснованных сгущений конечно-элементной сетки вблизи внутренних и внешних углов, ограничивающих поверхность детали, вокруг областей сшивания сегментов поверхности (которые в новой модели отсутствуют). При задании одинаковой густоты разбиения (normal) с пятикратным уменьшением размера конечных элементов в направлении нормали к поверхности детали количество конечных элементов составляет 78000 и 42000 для исходной и отредактированной моделей детали, соответственно. Благодаря использованию единой «теории» для детали и формообразующей оснастки, отсутствуют пересечения обеих областей моделирования и «пустые» элементы на разделяющей их поверхности. Полученная в результате редактирования CAD модель была проверена на встроенных конвертерах систем ABAQUS и Comsol Multiphysics (версии 3.5а, 5.1), не выявивших ошибок и успешно выполнивших преобразование геометрии модели.

Рис. 8. Результирующая поверхность новой «теории»

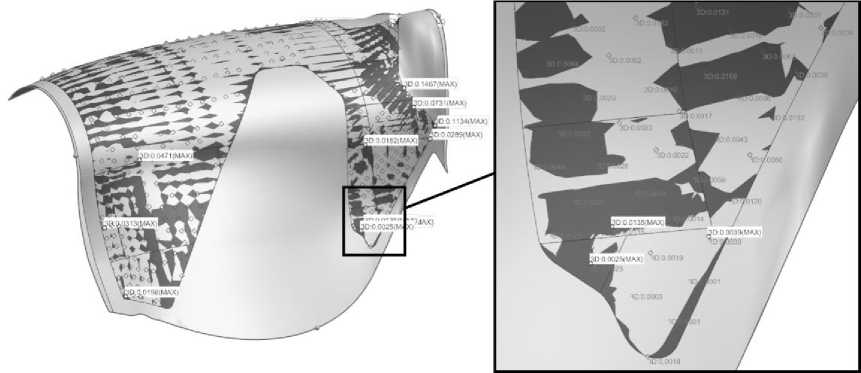
Рис. 9. Отклонения новой «теории» от исходной поверхности (Значения отклонений с указанием MAX являются максимальными в пределах границ одной исходной поверхности)

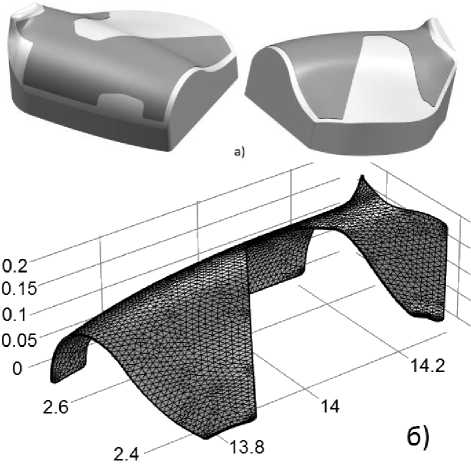
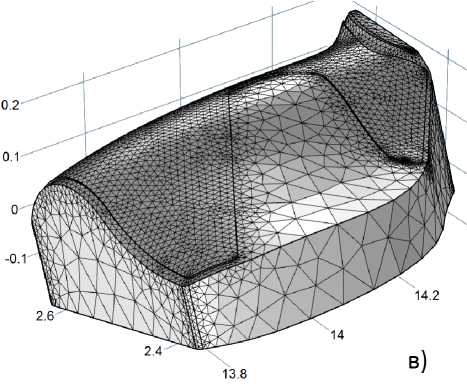
Рис. 10. Модель детали, совмещенная с моделью оснастки, построенные по новой «теории» (а) и результаты их конвертации в конечноэлементное представление (б), (в)

Выводы.                                 2.

• 1.    Разработан метод лидарно-томографичес-кого исследования планетарных атмосфер с помощью малых автоматических аппаратов.

• 2.    Созданы математические методы реконструкции искомых функциональных распределе- 3. ния на основе быстродействующих свёрточных алгоритмов.

• 3.    Проведенные исследования с помощью методов математического моделирования показали работоспособность предложенных мето- _4. дов исследования планетарных атмосфер. Погрешность алгоритмов реконструкции составляет 5-12%.

• 4.    Разработана конструкция малогабаритного ^5. лидара для использования его на нано- и микроспутниках.                                     _6.

Представленная работа выполнена в рамках реализации Государственного задания ЮНЦ РАН 007-0111416 (проект 0256-2015-0074) и гранта 15-08-00849 Российского Фонда фундаментальных исследований            7 _.