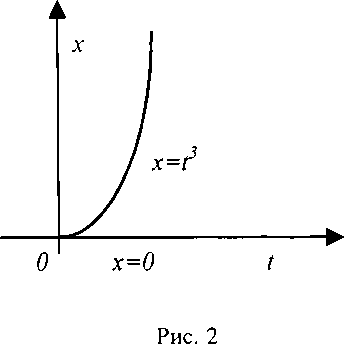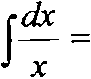Проблемы обучения построению математических моделей в системе школа - колледж - вуз

Рассмотрим дифференциальное уравнение, разрешенное относительно производной:

dx

— = Жх\ (7) at

Всякая функциях =

которая при подстановке в дифференциальное уравнение обращает его в тождество, называется решением этого уравнения.

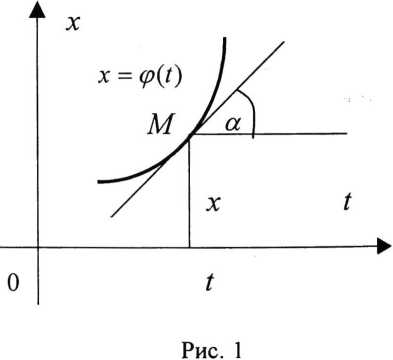
Построенный на плоскости Юх график всякого решения х = (р^ данного дифференциального уравнения называется интегральной кривой этого уравнения. Если рассматривать дифференциальное уравнение в виде (7) и обозначить через а угол между касательной к интегральной кривой х = ср^ в точке (/,х) и положительным направлением оси Ot (рис. 1), то, принимая во внимание, что tga = x, а х = /(Z,x), мы получим tga= f(t,x\ так что направление касательных к интегральным кривым задается самим дифференциальным уравнением.

Предполагается, что f(t, х) конечна в каждой точке рассматриваемой области. Если это не так, то наряду с уравнением (7) будем рассматривать перевернутое уравнение dt _   1

dx f^t,x^

Во многих вопросах теоретического и прикладного характера требуется среди всех решений дифференциального уравнения (7) найти решение х =

удовлетворяющее условию

^^^ 3, х = х0 при t = t0, (9)

где t₀ и х₀-заданные числа. Другими словами, требуется найти такое решение х = <р(0, в котором функция (р^ принимает заданное значение х₀, если независимую переменную / заменить заданным значением t₀, так что х(/₀) = х₀. Геометрически это значит, что требуется найти интегральную кривую, проходящую через заданную точку плоскости М_о Q^Xq).

Условие (9) называется начальным условием решения х = <р(Т), а числа t₀ и х₀ -начальными данными этого решения.

Задача нахождения решения, удовлетворяющего заданному начальному условию (9), называется задачей Коши.

Решение задачи Коши может оказаться не единственным, т.е. иногда существует несколько решений, удовлетворяющих заданным начальным условиям х = х0 при t=t0. Нельзя также утверждать, что задача Коши всегда имеет решение. Поэтому становится важным и необходимым изучение теорем существования и единственности решений дифференциального уравнения.

Теоремы существования и единственности задачи Коши имеют принципиальное значение, гарантируя законность применения методов теории дифференциальных уравнений для решения задач естествознания и техники. Они служат обоснованием для создания новых методов и теорий. Часто доказательства самих теорем существования и единственности являются конструктивными, т.е. методы доказательства дают и методы приближенного отыскания решений с любой степенью точности. Теоремы существования и единственности лежат в основе не только теории дифференциальных уравнений, но и численных методов интегрирования.

Численному интегрированию дифференциального уравнения обязательно должно предшествовать обращение к теоремам су-

2001 £Ж^^ ществования и единственности, чтобы избежать неправильных выводов.

Теорема существования. Если в уравнении

^ = /(<-*)        (Ю)

СП функция определена и непрерывна в некоторой области D121 плоскости Юх, то для любой точки (70, х0 ) € D существует решение х(/) задачи Коши dx

— = f(t,x),x(t₀) = x₀,   (И)

at определенное на некотором интервале, содержащем точку t0.

Теорема существования и единственности. Если в уравнении (10) функция f (t, х) и производная этой функции по х определены и непрерывны в некоторой замкнутой ограниченной области D на плоскости tOx . содержащей некоторую точку

(t₀, х₀), то существует единственное решение этого уравнения х = ср^Т), удовлетворяющее условию х = х₀ при t = t₀.

Геометрически смысл теоремы заключается в том, что существует, и притом единственная, функция х = (р^, график которой проходит через точку (Г0,х0 ).

Если функция f(t,x) имеет неограниченную производную по х в области D, то могут существовать несколько решений, удовлетворяющих задаче Коши (11).

Пример 5. Рассмотрим уравнение х = 3^         (12)

с начальными условиями х = 0 при t = 0-        (13)

Здесь производная функции З/Vx по х равна <х~2/3 —> оо при х —> 0

^ЖвЖ ИНТЕГРАЦИЯ ОБРАЗОВАНИЯ ЖЖ^^

В этом случае существуют два решения уравнения (12), удовлетворяющие начальным условиям (13): х = 0, х = t³

В том, что эти функции есть решения уравнения (12), убеждаемся непосредственной подстановкой их в уравнение. Через начало координат проходят две интегральные кривые (рис. 2).

Под общим решением дифференциального уравнения (7) будем понимать функцию х = ф^1, С), которая при любом значении произвольной постоянной С является решением данного уравнения, график которой целиком принадлежит G^[3).

Решения, которые получаются из общего решения х = ф((, С) при определенном значении произвольной постоянной С, называются частными. Однако встречаются дифференциальные уравнения, имеющие такие решения, которые не получаются из общего решения ни при каких значениях С. Такие решения называются особыми. Графиком особого решения является интегральная кривая, которая в каждой своей точке имеет общую касательную с одной из интегральных кривых, определяемых общим решением.

Разберем один из методов решения (интегрирования) дифференциального уравнения с разделяющимися переменными первого порядка.

Рассмотрим дифференциальное уравнение вида dx

7=/^Ш   (]3а)

dt где правая часть есть произведение функции, зависящей только от t, и функции, зависящей только отх. Преобразуем его следующим образом (предполагая, что №^0У

-l-dx^/^OdL (14) Л to

Считая х известной функцией от г, равенство (14) можно рассматривать как равенство двух дифференциалов, а неопределенные интегралы от них будут отличаться постоянным слагаемым. Интегрируя левую часть по х, а правую по /, найдем

[Д—д = Г(')»+с.

J/2to J

Мы получили соотношение, связывающее решение х, независимое переменное / и произвольную постоянную С, те. получили общий интеграл уравнения (13а). Под общим интегралом здесь понимается соотношение, связывающее t,x и произвольную постоянную С, данное в виде неразрешенного относительно х, те. у/(/,х,С) = 0 или i//(t,x) = C. Есть и другие типы интегрируемых дифференциальных уравнений (см.: Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. Минск, 1974; Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М., 1970; Шестаков А.А., Малышева И.А., Полозков Д.П. Курс высшей математики: Интегральное исчисление. Дифференциальные уравнения. В!екторный анализ. М., 1987).

В теории дифференциальных уравнений выделен класс интегрируемых дифференциальных уравнений. Поэтому, когда дифференциальное уравнение не относится к классу интегрируемых, дифференциальное уравнение интегрируют (решают) с помощью приближенных методов. Здесь не ста- вится целью изложение приближенных методов (с ними можно познакомиться в кн.: Боглаев Ю.П. Вычислительная математика и программирование. М., 1990; Пономарев К.К. Специальный курс высшей математики. Дифференциальные уравнения, краевые задачи, интегральные уравнения. М., 1974).

Очень важно правильно на основе фундаментальных законов, в рамках соответствующей отрасли науки составить математическую модель динамического процесса и выбрать метод решения.

Приведем примеры моделирования реальных процессов в экологии. Экология изучает взаимоотношение человека и животных организмов с окружающей средой. Основным объектом экологии является эволюция популяций.

Ниже описываются дифференциальные модели популяций, которые связаны с размножением или вымиранием последних, а также с сосуществованием различных видов животных в ситуации «хищник - жертва».

Пусть x(t) - число особей в популяции в момент времени Z. Тогда если А - число особей в популяции, рождающихся в единицу времени, аВ- число особей, умирающих в единицу времени, то с достаточным основанием можно утверждать, что скорость изменения x(t) со временем задается формулой

— = А-В. (15) dt

Задача теперь состоит в том, чтобы описать зависимость А и В от х. Простейшим случаем является ситуация, когда

А = ах, В = Ьх, (16)

где а и b - коэффициенты рождения и смерти особей в единицу времени соответственно. С учетом равенств (16) дифференциальное уравнение (15) перепишется в виде dx ,

— = (а-Ь}х. (17) dt

Из уравнения (17), разделяя переменные и интегрируя, получаем

J(a-^ + lnC(C>0), отсюда

x(t) = Ce^(a-^hV           (18)

Полагая, что в момент времени t = t₀

число особей в популяции есть х = х₀ , из уравнения (18) находим x(Z) = x_oe^Vu-^b*'"^,,a

Из полученного равенства следует, что если а > b , то при t -> оо число особей х —> со. С другой стороны, если а < b . то х —> 0 при t —> оо и популяция становится вымирающей.

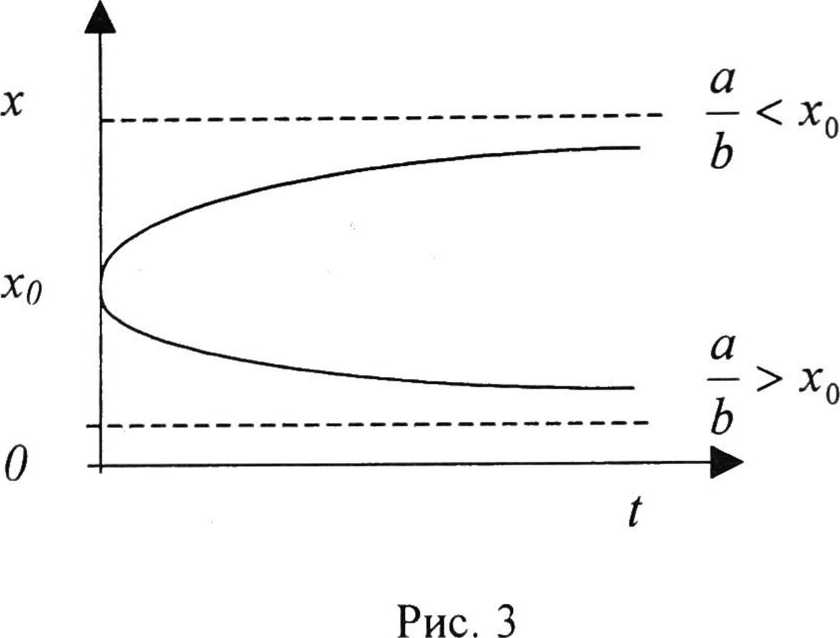
Хотя приведенная модель является упрощенной, она все-таки в ряде случаев соответствует действительности. Практически же все модели, которые описывают реальные явления и процессы, нелинейны, и вместо дифференциального уравнения (17) следует рассматривать уравнение вида dx

— = j\t,x\ dt где /(Z,x)-нелинейная функция.

В качестве примера рассмотрим частный случай этого уравнения, где функция /(/, х) зависит только от х:

— = /(х) = ах - Ьх1. dt где а > О, b > 0.

Полагая, что х = х0 при t=t0, из последнего уравнения находим, что хоа/Ъ х^ = —гти—; -«б-^~ (19) х0 +[я/6-х0]е

Отсюда видно, что при Z —> со число

а особей в популяции ^v ) ~При этом а       а возможны два случая: у > *о и у < *0 о        о

Различие между этими случаями хорошо видно на рис. 3.

Щ®^^ ИНТЕГРАЦИЯ ОБРАЗОВАНИЯ ^ЖЙ^^

Отметим, что соотношение (19) описывает, в частности, популяции вредителей фруктовых деревьев и некоторых видов бактерий.

Если рассматривают несколько видов, например больших и малых рыб, где малые рыбы являются кормом для больших, то, составляя дифференциальные уравнения сосуществования для каждого вида, получают систему дифференциальных уравнений

^- = /,(/,x,,...,xJ,z = 1,2,

at

Рассмотрим более подробно двухвидовую модель «хищник - жертва», которая впервые была построена В. Вольтерра для объяснения колебаний рыбных уловов в Адриатическом море, имеющих один и тот же период, но отличающихся по фазе.

Пусть х - число больших рыб-хищников, питающихся малыми рыбами-жертвами, число которых обозначим через у. Число рыб-хищников будет расти до тех пор, пока у них будет достаточно пищи, те. малых рыб-жертв. Но в конце концов наступит ситуация, когда корма не будет хватать и в результате число больших рыб начнет уменьшаться. Это приведет к тому, что с некоторого момента число малых рыб начнет увеличиваться. Данное обстоятельство будет способствовать новому росту числа больших особей, и цикл снова повторится. Модель, построенная Вольтерра, имеет вид

^ = -ах + Ьху, (20) си

— = сх-кху, (21) at где а,Ь,с,к - положительные константы.

В уравнении (20) для больших рыб слагаемое Ьху выражает зависимость прироста от численности малых рыб. В уравнении (21) слагаемое -кху выражает уменьшение числа малых особей в зависимости от численности больших.

Изучение сообществ, взаимодействующих более сложным образом, дает интересные практические результаты. Так, например, если две популяции конкурируют в борьбе за один и тот же источник питания (третья популяция), то можно показать, что один из видов начнет вымирать. При этом понятно, что если этим видом окажется источник питания, то такая же участь постигнет и два других вида.

В настоящей работе приводится достаточно полное изложение основ общей теории дифференциальных уравнений (определение дифференциального уравнения, его решения и графики решения). Изложены некоторые методы решения. Показано, что дифференциальные уравнения являются математическими моделями динамических процессов.

В колледже и вузе остается изучить более полно аналитические и численные методы решения дифференциальных уравнений. Помимо указанного, в вузе необходимо обратить внимание на теоремы о непрерывной зависимости и дифференцируемости решений по параметрам и начальным данным, вопросы теории устойчивости. Таким образом снимается педагогический барьер и достигается преемственность обучения как процесса.

ПРИМЕЧАНИЯ

¹¹¹ Окончание. Начало см. в № 2 за 2001 г. ¹²¹ Под областью D, понимается непустое множество точек G, обладающее свойствами: а) произвольная точка G имеет окрестность, принадлежащую D; б) множество G связано, т.е. две любые точки можно соединить ломаной, лежащей в D.

131 Приведенное определение не является строгим. Строгое определение общего решения дано в работе: Шестаков А.А., Малышева И.А., По-

лозков Д.П. Курс высшей математики: Интегральное исчисление. Дифференциальные уравнения. Векторный анализ. М., 1987.

УНИВЕРСИТЕТ В СИСТЕМЕ ДОВУЗОВСКОЙ ПОДГОТОВКИ УЧАЩИХСЯ

И.И. Борисов, ректор Воронежского государственного университета, профессор,

С.А. Запрягаев, первый проректор Воронежского государственного университета, профессор,

Развитие всех уровней системы образования, структурные и экономические преобразования в стране, возросшая роль автономии высших учебных заведений, децентрализация управления системой образования выявили ряд тенденций, приводящих к отрыву возрастающих требований системы высшего профессионального образования к выпускникам средних школ от уровня, достигаемого учащимися в школе.

Такое положение и стремление высших учебных заведений к пополнению студенческой среды наиболее подготовленными и профессионально ориентированными учащимися стимулирует процесс раннего «проникновения» системы высшего образования в среду общего среднего образования, создавая комплекс условий для обеспечения плавного, целенаправленного непрерывного образования.

Реализуя программу интеграции систем образования, Воронежский университет проводит такую работу по нескольким основным направлениям.

• 1.    Включение общеобразовательных учебных заведений в состав и структуру университета. На сегодняшний день это гимназия Н.Г. Басова, педагогическая гимназия № 5 и гуманитарная гимназия № 2 (Воронеж), Верхнемамонская школа (Воронежская обл.). В официальном наименовании каждого такого учебного заведения указано «при Воронежском госуни-верситете». И это не формальное уточнение, а выражение сущностной особенности учеб-ного заведения, закрепленной комплексом контактов и договоров с университетом.

• 2.    Создание специализированных классов (с углубленным изучением учебных дисциплин) в школах, имеющих с университетом договор о сотрудничестве. Задача таких классов - оказать учебно-методическую поддержку продвинутому школьному образованию для групп учащихся конкретной школы. Обычно эти классы способствуют ранней профессиональной ориентации учащихся и расширению их кругозора в одном определенном направлении. Накопленный опыт, учитывающий интересы и устремления учащихся, чаще всего приводит к формированию классов физико-математического, химико-биологического, экономического и историко-филологического профиля. Набор учащихся в них, формирование учебно-методической документации и организация учебного процесса осуществляются при непосредственном участии университетских преподавателей. Договор со школой заключается на срок от 3 до 5 лет, а его выполнение постоянно анализируется и контролируется совместно школой и университетом.

Содержание данных договоров включает в себя совместное составление рабочих учебных планов и программ учебных дисциплин и их методического обеспечения, широкое участие университетских преподавателей в учебном процессе школы. За статусом «школа при вузе», как правило, стоит многолетний опыт совместной работы школы с факультетами и кафедрами ВГУ.

В настоящее время университет имеет договоры о сотрудничестве с 40 школами города и области, обеспечивая одновремен-