Процессуальные задачи как средство развития математического мышления

Долгое время главной целью в обучении математике было наполнение учащихся знаниями, умениями и навыками. Сегодня, в связи с обновлением целей обучения, особое внимание уделяется развитию творческого мышления учащихся. Именно оно является основой интеллектуального развития личности, которое, в свою очередь, составляет главное богатство любого государства, заботящегося о своем будущем. При этом обучение математике должно опираться на следующие теоретические концепции: развитие личности, организация самостоятельной творческой деятельности обучаемых, дифференцированный и индивидуальный подход к ним.

Главным в процессе обучения математике во все времена было, есть и будет содержание школьного математического образования. В этом направлении, особенно в последние годы, делается многое. Издается большое количество учебников, сборников задач для школ. Однако работ по организации самого процесса обучения математике явно недостаточно. Чтобы восполнить этот пробел, опишем некоторые результаты нашего многолетнего исследования по использованию процессуальных задач в обучении математике.

Процессуальными мы называем зада чи, в которых находится идея (алгоритм) их решения. Основная особенность таких задач заключается в том, что ответом является не какой-либо математический факт, а сам процесс его получения. В задачах изначально известны конечная цель и условия, накладываемые на процесс ее достижения; требуется найти, спланировать и описать или проговорить устно этот процесс. Подобные задачи обладают высоким потенциалом осуществления на практике идеи развивающего обучения математике.

Решение процессуальных задач способствует развитию у учащихся не только общеинтеллектуальных умений, но и, что самое главное, математического мышления, дает возможность вовлечь ребят в творческую поисковую деятельность. Эти задачи носят эвристический характер, т. е. направлены непосредственно на открытие решения. Одним из основных значений процессуальных задач является то, что их решение задействует и, следовательно, формирует операционный стиль мышления, который необходим при изучении всех дисциплин, в частности математики. Умение решать процессуальные задачи имеет большое практическое значение, так как в жизни встречаются такие проблемы, которые требуют найти именно способ достижения желаемого результата. Мы работаем над созданием системы задач на открытие обучаемыми пути их решения.

Приведем некоторые из примеров процессуальных задач, которые мы апробировали на факультативных занятиях в различных типах школ.

• I.    Проговорите процесс решения задачи.

На координатной плоскости изобразите все точки М (х, у), координаты которых удовлетворяют следующим неравенствам:

• a)    cos (х + у)²< cos (х - у)², 0 < х<3, О < у < 3;

• б)    cos²x sin у + cos²y sin х > 0;

• в)    2arccos х > arccos у;

у —2 I sin х I

• II.    Каково начало решения уравнения?

• 1)    X⁵ + (х + I)⁵ + (х + 2)⁵ + ... + (х + + 1998)Д=Л;________

• 2)    ^v2 + ЪГТ^П + х = х;

• 3)    (х + 1) (х + 2) (х + 3) (х + 4) = 100;

• 4)    х⁴ - 2х³ - Зх² + 4х = 4;

• 5)    2(х² + х + 1 )² — 7(х - I)² = 13 (х³ -- 1);

• 6)    (х⁴ - 4х² + 2)⁴ - 4(х⁴ - 4х² + 2)² = = х - 2;

• 7)    (х - 2)⁶ + (х - 4)⁶ = 64;

• 8)    (х - I)⁵ + (х + З)⁵ = 242 (х + 1);

• 9) |...| | |х²-х| -1 | -1 |...-1| = = х²-2х - 14;

• 10)    х³ + х² + х + х ¹ + х ² + х ³ = 6;

• 11)    5х⁶- 16х⁴ - ЗЗх³ - 40х² + 8 = 0.

• III.    Проговорите идею решения систем

уравнений:

sin х sin у = 3/4, tg X tg у = 3;

sin х cos у = a, cos x cos у = b (a ^ 0, b * 0);

21ogi-x(-xy - 2x + у + 2) +

. + log2+y(x2 - 2x + 1) = 6;

logi-x(y + 5) - log2+y(x + 4) = 1;

4) pogyX - logxy = 3, xy = 16.

• IV.    Как найти два корня уравнения 5х⁶- 16х⁴ - ЗЗх³ - 40х² + 8 = 0, произведение которых равно 1?

• V.    Как найти количество решений уравнения {х[х|} = 0,5, удовлетворяющих условию 1 < х < 5?

• VI.    Проговорите план решения задач. Постройте треугольник:

• 1)    по трем медианам;

• 2)    по трем высотам;

• 3)    по заданному отношению сторон и сумме медиан;

• 4)    по двум углам и периметру треугольника;

• 5)    по сторонам а и b и биссектрисе угла С.

• VI I. Объясните процесс построения

графиков соответствий:

= а

У

у

= 2;

I х

-2 1-2 1 =

х

= | sin х | ;

= - | cos I X I I ;

= -2sin | x | ;

= 2cos | 3 | х | + 5 | ;

• VI II. Проговорите алгоритм решения задач.

• 1)    В новогоднюю ночь на подоконнике стояли в ряд (слева направо) герань, крокус и кактус. Каждое утро Маша, вытирая пыль, меняет местами цветок справа и цветок в центре. Днем Таня, поливая цветы, меняет местами тот, что в центре, с тем, что слева. В каком порядке будут стоять цветы через 365 дней в следующую новогоднюю ночь?

• 2)    При любом натуральном п (п² + + 5) делится на 6. Найдите п.

• 3)    Для каких любых целых пит число пт (п — т) является четным?

• 4)    Произведение каких двух последовательных четных чисел делится на 8?

• 5)    Если р и (2р + 1) — простые числа,

p > 5. то (4p + 1) — число составное. Найдите p.

• 6)    Найдити число р, если известно, что р, (р + 2) и (р + 4) — простые числа.

• 7)    Найдите все р, для которых р, р + 10 и р + 20 являются простыми числами.

• 8)    При каких значениях х и у число 34+ 5у делится на 36?

• 9)    Какой цифрой оканчивается число, получаемое в результате следующего возведения в степень: а) 35 352^{1 98}°; б) 24 567^{1 980}; в) 1 999* ⁹^; г) 777⁷⁰⁰; д) 223 345⁷⁰⁰?

• 10)    Найдите наименьшее натуральное число, которое при делении на 5, 6 и 7 дает в остатке соответственно а) 2, 3 и 4; б) 1. 4 и 3.

• 11)    Найдите все натуральные числа, больше 200, но меньше 1 500, каждое из которых при делении на 8 дает в остатке 5.

• 12)    Сравните числа: а) 2³⁰⁰ и З²⁰⁰; б) е¹¹ и п^с; в) З³⁴ и 2^; г) 202³⁰³ и ЗОЗ²⁰²; д) log₄5 и log₆5; е) log₉10 и log^ll; ж) log32 и log23; з) log532 и log25; и) log]6729 и log316.

• 13)    В группе из 100 туристов 70 человек знают английский язык, 45 знают французский язык, и 23 человека знают оба языка. Сколько туристов в группе не знают ни английского, ни французского языка?

Процессуальные задачи особенно полезны:

• 1)    в ходе итогового обобщающего повторения темы, раздела, всего курса;

• 2)    в ходе подготовки к контрольной работе, к выпускным экзаменам в школе и вступительным экзаменам в вузы;

• 3)    при подготовке к общероссийскому тестированию. В этот период выпускникам школ нужно в короткий промежуток времени решить большое количество задач на самые разные темы всего школьного курса математики. Весьма существенно то, что надо найти их оптимальные решения, так как при тестировании учащиеся должны довести решения до конечного ответа, именно он учитывается при оценивании.

К работе по составлению систем задач мы привлекаем студентов математического факультета Мордовского госунивер-ситета и самих учащихся. Некоторые материалы подбираются из различных источников, таких, как:

— учебные пособия и сборники задач для факультативных и внеклассных занятий по математике;

— публикации, посвященные Соро-совским математическим олимпиадам. В них обычно не вносится ничего намеренно усложненного; задачи содержат, как правило, только материал школьных программ и учебников; подчеркиваются, где это возможно, те моменты, которые ясно указывают на связь материала школьных программ и учебников с сегодняшними результатами науки. Есть задачи, посильные каждому хорошо успевающему школьнику, и задачи повышенной трудности, которые в состоянии решить тот, кто глубоко и самостоятельно мыслит, умеет применять школьные знания на практике. Такие задачи требуют упорной работы и настойчивости, способности разобраться в неожиданном и найти собственный путь решения;

— сборники задач для поступающих в вузы.

Особенно полезна работа по составлению задач студенту — будущему учителю. Общеизвестна истина, что, прежде чем кого-то учить, необходимо самому уметь постоянно учиться, практически владеть приемами определенного вида работы. К. Д. Ушинский писал: „Мы по большей части учим так, как нас самих учили, и исключения из этого правила слишком редки, чтобы можно было на них рассчитывать в деле народного об-разования" (Ушинский К. Д. Проект учительской семинарии // Собр. соч.: В 11 т. М., 1948. Т. 2. С. 522).

Будущий учитель отбирает системы процессуальных задач различного уровня сложности, участвует в нахождении различных способов решения задач и готовится теоретически и практически к инновационным методам ведения занятий по математике.

Назовем лишь некоторые проблемы исследований, проводимых объединенными группами преподавателей и студентов университета совместно с учителями школ Мордовии:

• 1)    разработка концептуальных положений и практических технологий по совершенствованию учебного процесса и качества обучения учащихся и студентов;

• 2)    разработка систем внеклассных и факультативных занятий по математике для традиционных и новых типов школ;

• 3)    деятельностный подход в организации внеклассной работы по математике;

• 4)    инновационные методы ведения занятий по математике;

• 5)    системный подход к составлению задач школьного курса математики;

• 6)    нестандартные формы и средства контроля при изучении математики и др.

Для организации индивидуальной деятельности обучаемых и их самоконтроля результатов обучения нами составляются многоуровневые многовариантные тестовые задания. При этом мы стараемся,

Укажите множество точек плоскости (рис. 1 — 9>, координаты которых чтобы задания максимально содействовали развитию творческого мышления учащихся. Как показывает наш многолетний опыт работы в естественно-техническом лицее при Институте физики и химии Мордовского госуниверситста, в малой школьной академии при школе № 36 и в математических классах школы № 32 г. Саранска, процессуальные задачи являются эффективным средством развивающего обучения математике.

Ниже приведем одно из тестовых заданий, которое составлено студенткой III курса Т Нестеровой. С удовлетворяют одному из девяти соотношений.

1-й уровень

• 1)    у = 1 - 2sin х; 2) у = sin | х | ;

I          I ex            sin X

• 4)    у = sec х cos х ;   5) у = -т—:----г-

• J                   1           1 J I sin X |

• 7)    | у | = cos x; 8) у = cos x + | cos x | ;

  3) у = | cos x | ;

  6) у = tg X etg x;

  9) у = | tg x |

  
  
  

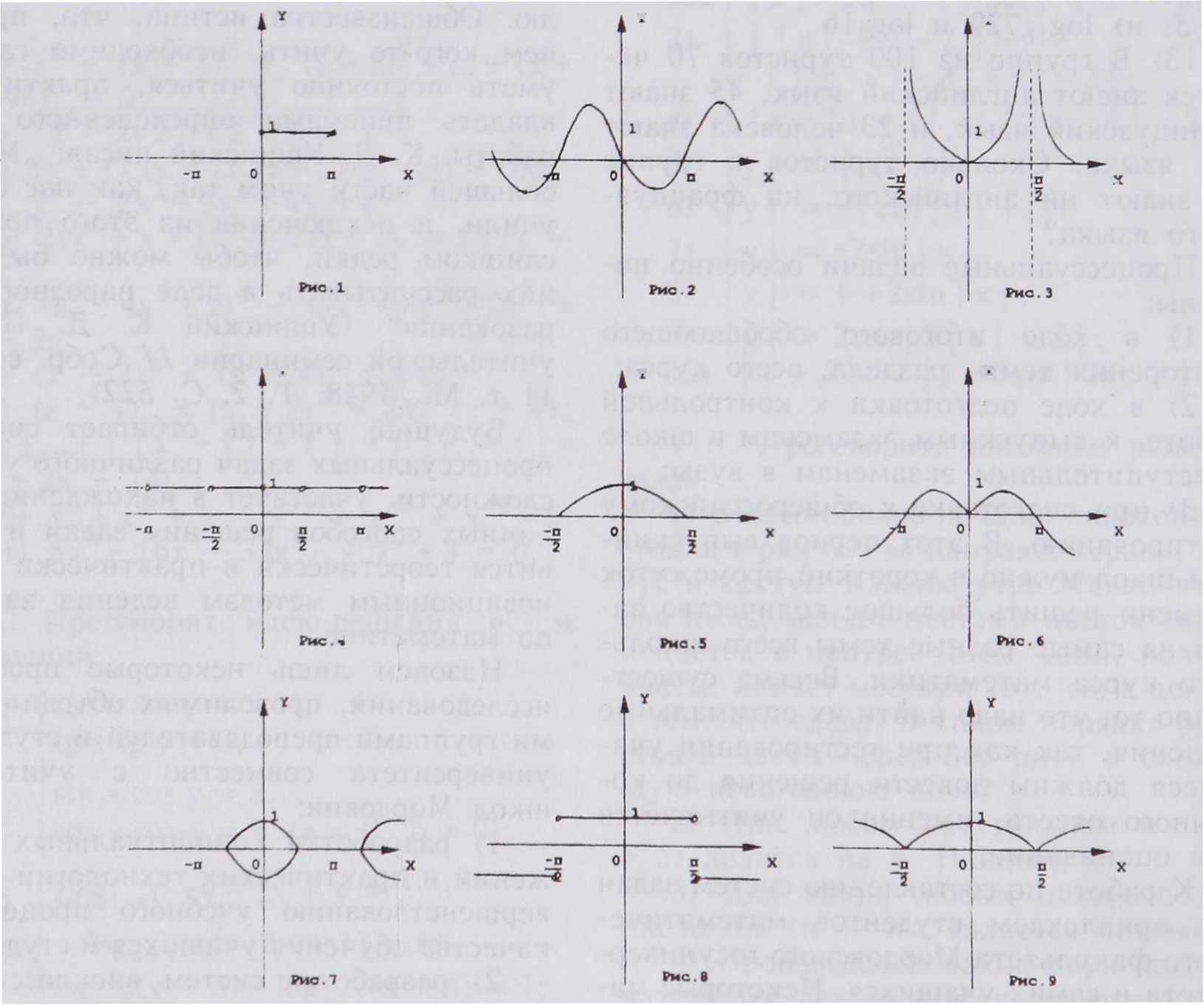
  Ответы: 1) рис. 2; 2) рис. 6; 3) рис. 9; 4) рис. 8; 5) рис. 1; 6) рис. 4;

  7) рис. 7; 8) рис. 5; 9) рис. 3.

  
  

  1999. No 2

2-й уровень

1) у = I cos 2х I ; 2) у = -pVtg х; 3) у = T-Sm х . ;

I х I                             I sin X I

4) у = | tg х | ; 5) у = sin х + I sin х | ; 6) у = -i cos х ■ - cos х v 1 - COS X

'^ ^ - cos х : 8) у = cig х | sin х | ; 9) | х | = х cos 2ny.

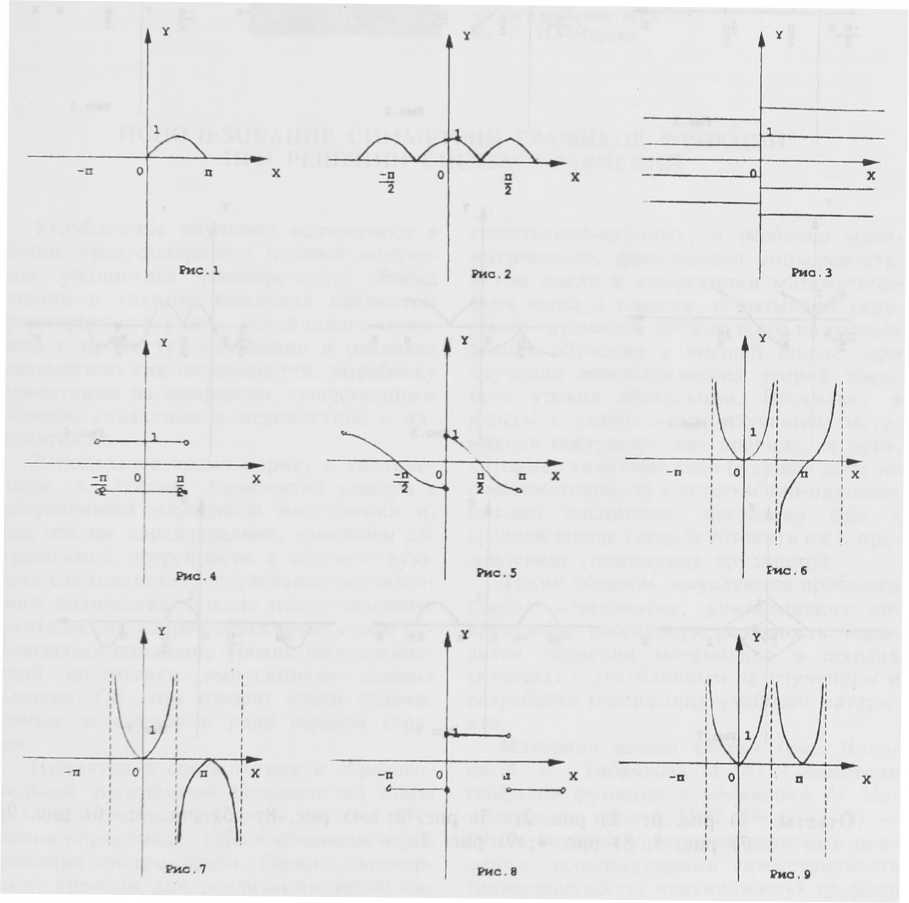
Ответы: 1) рис. 2; 2) рис. 6; 3) рис. 8; 4) рис. 9; 5) рис. 1; б) рис. 4;

7) рис. 7; 8) рис. 5; 9) рис. 3.

3-й уровень

, sin х + sin Зх _ sin х I 2х I                    э / /---.      ■ 2 , /---.

Ь у • ЛиТТх-ТГ ; 21 У " “sin xl ; 31 у " “s №х) + хт (Лё х);

4) у = | sin х | - sin | х | ; 5) у = cln< со& х); 6) у = sin х Vcos2x + cos х Vsin2x;

7) у = sin х

1 - sin ²x

; 1 \ ">  У Vsin^zx

| cos х | tg | x | ; 9) cos n

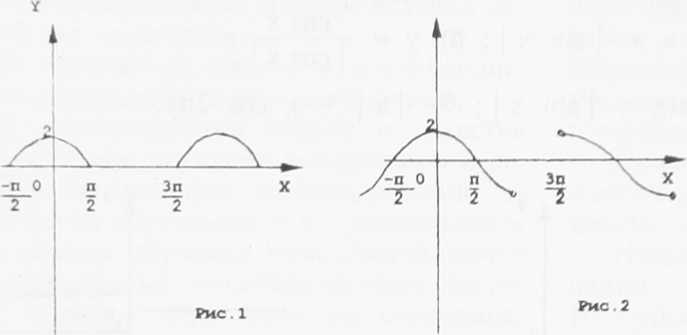
( I X I + I у I ) = 0.

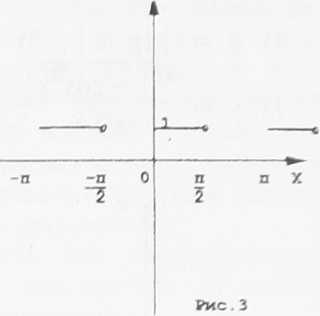
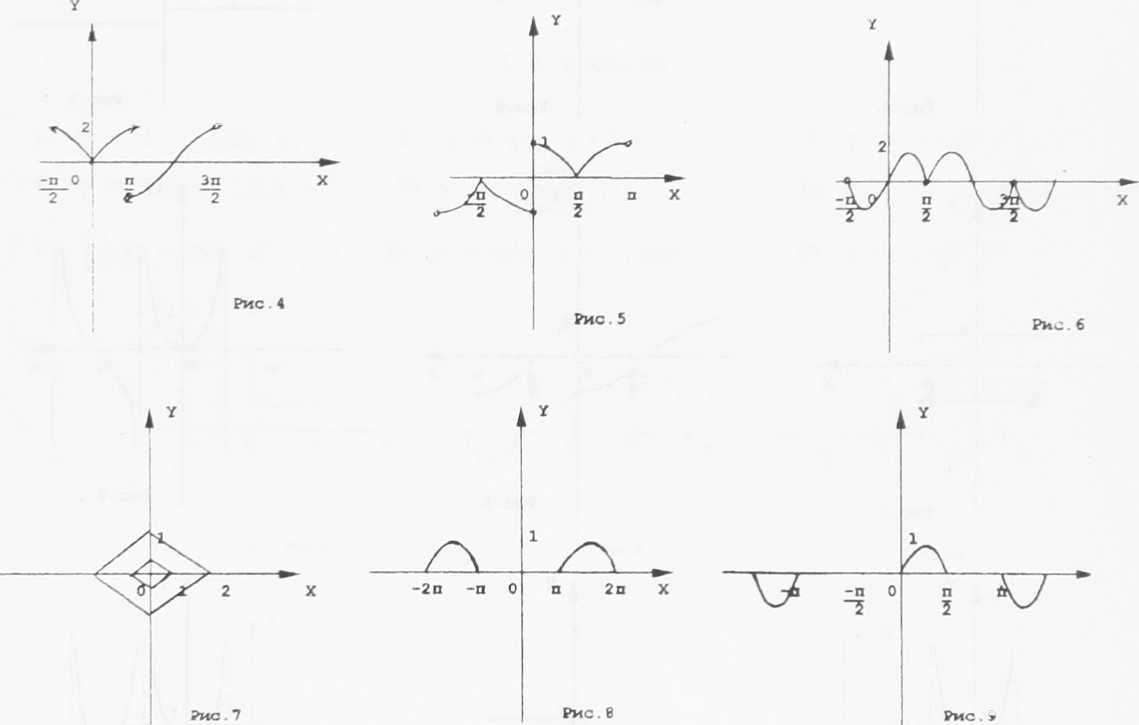
Ответы: 1) рис. 6; 2) рис. 2; 3) рис. 3; 4) рис. 8; 5) рис. 1; 6) рис. 9;

7) рис. 5; 8) рис. 4; 9) рис. 7.