Прочность каменной кладки сводчатых конструкций

Каменная кладка – один из древнейших строительных материалов. До наших дней дошло множество произведений архитектурного искусства, выполненных в каменной кладке. Долговечность и надежность таким сооружениям обеспечила развитая технология кладки, совершенствовавшаяся сотни и тысячи лет. В основном это был эмпирический опыт и лишь в последние века начали появляться теоретические прочностные модели кладки и численные методы ее расчета. Вертикальные каменные элементы – стены и колонны были сравнительно просты в расчете, так как находились в состоянии одноосного сжатия. В начале XX века появилась устойчивая теория их расчета, основанная на исследованиях Л. И. Онищика [1, 2]. Однако в это же время начинается расцвет металлических и железобетонных конструкций и исследования каменной кладки уходят из приоритетных задач строительной науки. Каменные арки и сводчатые перекрытия так и не получили полноценной теории, описывающей условия их прочности [3].

Исторически сложились пять основных теорий прочности, на основе которых разработаны многочисленные частные критерии прочности для различных материалов и напряженных состояний. Первая теория основывается на предположении, что причиной разрушения материала являются наибольшие по абсолютному значению нормальные напряжения:

^ст экв = ^ст 1 <И ,                                                              (1)

где ст_экв - расчетное напряжение в конструкции;

ст₁ - первое главное напряжение;

[ст] - максимальное допускаемое нормальное напряжение.

Первая теория подходит только для случая хрупкого растяжения, когда напряжения ст₂ и ст₃ намного меньше, чем ст₁ .

По второй теории прочности считается, что причиной разрушения являются наибольшие линейные деформации. Соответственно, критерий прочности:

СТ экв = CT i -v⁽ct2 +ст₃) < ^[ст^],                                   (2)

где v - коэффициент Пуассона;

ст₂ и ст₃ - второе и третье главные напряжения.

Вторая теория хорошо описывает случай хрупкого разрушения при одноосном сжатии, но при иных вариантах напряженно-деформированного состояния приводит к ошибочным результатам.

Согласно третьей теории прочности, причиной разрушения материала являются наибольшие касательные напряжения. Условие прочности по третьей теории:

СТ экв = CT i -Ст з < ^[ст^],                                            (3)

Третья теория дает удовлетворительные результаты для пластичных материалов с погрешностью до 10-15%, но не годится для хрупких.

В основе четвертой теории прочности лежит предположение о том, что причиной наступления предельного состояния в форме течения является удельная потенциальная энергия изменения формы, а не напряжения или деформации. Условие прочности:

СТ экв = J| ^[(СТ 1 -СТ 2 ⁾² + ⁽СТ 2 -СТ з ⁾² + ⁽СТ з —CT i ^)2]< ^[СТ^],                      ⁽⁴⁾

Четвертая теория используется для пластичных материалов и хорошо согласуется с опытными данными.

По теории прочности Мора прочность при любом напряженном состоянии будет обеспечена, если круг Мора не выходит за пределы огибающих кругов, построенных на допускаемых напряжениях при простом растяжении и сжатии. Упрощенное условие прочности, когда огибающие заменены прямыми:

Construction of Unique Buildings and Structures, 2016, №11 (50)

^а экв

= ^а 1

—

[ТГ^{3 5 и [Т} С ^]

где [Т р ] и [а с ] - максимальные допускаемые напряжения при одноосном растяжении и сжатии.

Теория Мора используется для хрупких материалов.

Стоит отметить, что данные критерии годятся только для однородных и изотропных материалов и не могут учитывать анизотропии прочностных свойств. Кроме того в случае сложного сопротивления для каждого напряженно-деформированного состояния необходим отдельный критерий прочности. Так, например, пластичная сталь при всестороннем растяжении проявляет хрупкие свойства, а хрупкие материалы при всестороннем сжатии начинают вести себя как пластичные.

Кирпичная кладка обладает ярко выраженной анизотропией по направлениям, перпендикулярным горизонтальным и вертикальным швам, что обусловлено ее структурной неоднородностью и технологией производства работ. Кладка имеет различную прочность на сжатие, растяжение, изгиб и сдвиг в зависимости от направления действия нагрузки. Так же прочность всегда заметно меньше по неперевязанному сечению, чем по перевязанному.

При сложном напряженном состоянии прочность зависит от угла наклона нагрузки к горизонтальным швам. Так, в работе [4] описана серия испытаний образцов кладки при двухосном растяжении со сжатием под углом наклона горизонтальных швов 0; 22,5; 45; 67,5 и 90 градусов к сжимающей нагрузке. Наименьшая прочность была получена под углом 45 градусов, а наибольшая – под углом 90 градусов. В целом испытания показали наличие сложной зависимости прочности кладки от соотношения между растягивающей и сжимающей нагрузкой и угла наклона горизонтальных швов. Схожие результаты были получены при конечно-элементном моделировании процессов разрушения образцов кирпичной кладки [5-8].

Проблемам трещиностойкости и прочности каменных конструкций посвящено большое количество работ В.Н. Деркача и Р.Б. Орловича [9-11]. Значимый вклад в теорию прочности кладки внес О.В. Кабанцев [12], однако в его работе основной упор сделан на сейсмические воздействия и рассматривалось только плоское напряженное состояние. В.В. Пангаевым была предложена расчетная модель определения прочности каменных конструкций [13], однако она выполнялась в программном комплексе «SCAD», который недостаточно приспособлен для анализа каменных конструкций [14]. Из зарубежных авторов следует выделить G. Milani [15, 16], который занимался исследованиями моделирования каменных сводчатых конструкций и внес большой вклад в теорию их прочности. Также стоит отметить L. Binda [17, 18], которая активно занимается вопросами долговременной прочности каменной кладки и провела большой объем исследований скрытых дефектов кладки, способов их обнаружения неразрушающими методами и моделирования поведения таких конструкций.

К настоящему моменту существует необходимость в устойчивой теории прочности сложных каменных конструкций – криволинейных, сводчатых и других, находящихся в сложном напряженном состоянии. Ее появление может существенно упростить и унифицировать расчеты, производимые при обследовании каменных зданий, составлении проектов их реставрации и реконструкции, решить проблемы прочности кладки современных фасадных систем. Помимо этого, такая теория может дать толчок к возрождению каменных конструкций в новом строительстве.

2.    Цели и задачи

Цель данной работы – определить возможность создания прочностной модели для кладки сводчатых конструкций и разработать алгоритм получения такой модели.

В число решаемых задач входит:

• •    анализ существующих на сегодня способов определения прочности кладки, разработанных в последние десятилетия;

• •    конечно-элементное моделирование конструкций кирпичных сводов и их расчет для сопоставления гомогенного и гетерогенного методов моделирования кладки и оценки их эффективности при определении прочностных, деформационных характеристик кладки и при анализе сводчатых конструкций.

3.    Разработанные методы определения прочности кирпичной кладки

Construction of Unique Buildings and Structures, 2016, №11 (50)

Прочность анизотропных материалов, в частности, каменной кладки достаточно подробно была исследована Г.А. Гениевым [19]. Он был практически единственным, кто занимался разработкой критериев прочности каменной кладки, однако не оставил своей школы и после него в России не было исследователей, занимавшихся этими вопросами достаточно глубоко. Г.А. Гениевым было сформулировано [20] аналитическое выражение для критерия прочности кладки при плоском напряженном состоянии, в общем случае в виде:

(R_CnCos²0 + R„. ¹ sin ² ^)(R_OT ¹ cos ² ^ + R j^ sin²p}a? — [(R^ ^ R^ ¹ + й_а1 ¹ йпн) — Ш Ln pU pH 1 LU рп Ln pH

• ^R co ¹ (^R lo^{1 + +}(^R pn" ^{— R} lu^{1 ) +} (^R ph ^—R lh" ⁾) ^— (^R lu¹ — ^нЭС^ И ^—R pH )^si^^^cos^] ° 1 ° 2 ⁺ (RcnSin²P + +R₍ r _H ¹ cos ² ^)(R p" _n ¹ sin ² ^ + R p^ cos ² ^)^ — [(R p"n Cos ² ^ + R p^m² ^) — (RcnCos²P + +R₍ r _H ¹ sin ² ^)]a₁ — [(Rp"nSin ² ^ + Rp^cos ² ^) — (R₍ r _n ¹ sin ² ^ + R^cos ² ^)^ — 1 = 0 ,

где R сн – прочность кладки на одноосное сжатие перпендикулярно горизонтальным швам;

R сп – предел прочности на одноосное сжатие перпендикулярно вертикальным швам;

R рн – предел прочности на одноосное растяжение перпендикулярно горизонтальным швам;

R рп – предел прочности на одноосное растяжение перпендикулярно вертикальным швам;

R со – предел прочности при двухосном равномерном сжатии;

• ^ - угол между направлением напряжения а₁ и горизонтальными швами кладки.

Выражение (6) представляет собой уравнение семейства эллипсов в осях а₁ , а₂ и подходит для случаев двухосного сжатия и двухосного растяжения. Для учета случая смешанного растяжения со сжатием используется уравнение семейства гипербол в виде:

а ² — 2(1 + 2к ² )а₁о'₂ + о-₂ —2k(c_U + с_н)(а₁+а₂) + 2к(с_п — c_H)(siu2^ + +kcos2^)(a₁—o'₂) — 4c_nc_H = 0 ,

где k – коэффициент внутреннего трения кладки;

• с_п - предел прочности на сдвиг по сечению, параллельному вертикальным швам;

• с_н - предел прочности на сдвиг по сечению, параллельному горизонтальным швам.

С использованием уравнений (6) и (7) наиболее удобно графически определять прочность кладки в главных напряжениях при сложных напряженных состояниях (рис. 1). В точках взаимного пересечения кривых A и B меняется механизм разрушения: раздробление-сдвиг-отрыв-сдвиг-раздробление. Полученный график практически полностью совпадает с результатами многочисленных испытаний образцов кирпичной кладки.

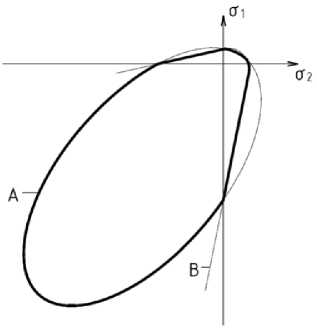
Рисунок 1. График пределов прочности кладки по критерию Г.А. Гениева

Construction of Unique Buildings and Structures, 2016, №11 (50)

В зарубежных исследованиях критерий прочности выводился как зависимость между предельными нормальными и касательными напряжениями. В частности, критерий Мюллера-Мана [21, 22], лежащий в основе европейских норм расчета каменных конструкций определяется тремя случаями разрушения:

Срез по горизонтальному шву:

М <

с — а_пк

1 + к^

^ т

где |т| - модуль касательного напряжения;

• а_п - нормальное напряжение;

• h m – высота горизонтального шва;

• b m – глубина перевязки кладки;

c – касательное сцепление кирпича с растворным швом. Отрыв:

|т| < 0,45й р _О

F5

где Rро – предел прочности при двухосном равномерном растяжении.

Раздробление:

|Т| <(йсн О"п)

Ь т ^ т

Следует упомянуть, что как в работах авторов этих критериев, так и в современных исследованиях по данной теме [23, 24], отмечено, что использование критериев возможно лишь при наличии входных данных, требующих большого количества прочностных испытаний конкретных видов кладки на одно- и двухосные нагружения.

Немалое значение имеет и моделирование процессов разрушения каменных конструкций, позволяющее получить сравнительно точные прочностные характеристики кладки. Основы такого моделирования были заложены P.B. Lourenço [25]. В его работе предложено три подхода к моделированию:

• 1)    Подробная гетерогенная модель – кирпич и раствор моделируются отдельными элементами, а взаимодействие между ними происходит через дополнительный элемент поверхности с фиктивной жесткостью. Для кирпича и раствора задают упругие и прочностные характеристики, а элементы поверхности взаимодействия моделируются как потенциальные плоскости сдвига и трещинообразования. Эта модель показывает наиболее точные результаты и может использоваться для моделирования испытаний образцов каменной кладки или отдельных узлов каменных конструкций. Для моделирования крупных конструкций такой подход не годится в виду сложности модели и ее ресурсоемкости.

• 2)    Упрощенная гетерогенная модель – раствор и поверхность взаимодействия сведены в единый плоский элемент, а размеры кирпича увеличены на величину растворного шва. Модель менее ресурсоемка, чем первая, однако ее точность уменьшена из за неучтенного коэффициента поперечной деформации растворного шва.

• 3)    Гомогенная модель – кладка моделируется сплошной, однородной и анизотропной. Для каждой оси анизотропии задается два параметра, соотносящихся с неупругими деформациями и характеризующих механизм разрушения при сжатии и растяжении. Модель предпочтительнее для достаточно больших объектов, когда нужен компромисс между точностью и эффективностью.

4.    Результаты моделирования каменных сводов

Исходя из данных подходов, наиболее эффективным представляется получение прочностных характеристик кладки из подробной гетерогенной модели и использование их в гомогенной модели. С учетом того, что все характеристики компонентов кладки либо известны, либо их получение не вызывает существенных затруднений (хотя на данный момент и нет единой методики, дающей достаточно точные результаты [26-28]), ее поведение может быть предсказано без дорогих и многочисленных реальных испытаний [29-31]. К недостаткам данной гомогенной модели можно отнести ее усложненность анизотропией. Как показала серия исследований [32-36], напряжения в изотропной и анизотропной моделях кладки не имеют сколько-нибудь значимых различий. Для определения прочности отдельных участков конструкции достаточно знать величину главных напряжений и их ориентацию относительно растворных швов. Кроме того, в некоторых сложных каменных конструкциях (например, сводчатые системы с разнотипными распалубками, наклонные криволинейные стены, и т.д.) задание линий анизотропии либо крайне неудобно, либо невозможно без существенных потерь в точности.

Результаты моделирования образцов кирпичной кладки P.B. Lourenço [37, 38] и прочностная гипотеза Г.А. Гениева практически полностью совпадают с результатами экспериментального исследования A.W. Page [39, 40], который провел испытания более сотни кирпичных панелей под различными углами наклона и сочетаниями нагрузок. Это свидетельствует о высокой достоверности описанных моделей.

Однако данные модели и результаты испытаний были получены для плоских конструкций прямоугольной формы. По сути, они находятся в строгой взаимосвязи с механизмом разрушения именно таких образцов и применимы только для каменных стен и столбов. Сводчатые же конструкции имеют другую форму и у них иная механика разрушения, равно как и у других каменных конструкций, находящихся в условиях объемного напряженного состояния.

В настоящее время сводчатые конструкции моделируются, как сплошное изотропное тело, а прочность определяется по максимальным допускаемым главным напряжениям.

Предполагалось на примере кирпичных сводов оценить возможность использования гетерогенной модели – как для определения прочности таких конструкций, так и для проведения виртуальных испытаний образцов кладки. В программном комплексе Abaqus были смоделированы простые цилиндрические своды с постоянными толщиной 0,25 м, пролетом 3 м, шириной 1,5 м и различной стрелой подъема. Все характеристики сводов и их конечно-элементных моделей сведены в таблицу 1.

Таблица 1. Исходные данные моделирования

№ п/п	Используемая модель	Стрела подъема, м	Объемный вес элементов, кг/м3		Количество элементов
1	Гомогенная	0,5	1800		3380
2		1	1800		4108
3		1,5	1800		5096
			Кирпич	Раствор	Кирпич	Раствор
4	Гетерогенная	0,5	1750	2000	656	10352
5		1	1750	2000	1648	18664
6		1,5	1750	2000	2480	22584

В опорных пятах сводов принято жесткое защемление. В обоих рассматриваемых способах моделирования конечно-элементные модели выполнялись с помощью объемных элементов. В гетерогенной модели соединение элементов раствора и кирпича принималось жёстким. Размер кирпича принят стандартным 250x120x65 мм, а толщина вертикальных и горизонтальных растворных швов – 10 мм. В качестве нагрузки во всех случаях было взято действие только собственного веса. Упругие характеристики кирпича и раствора были приняты по данным [41]: для кирпича модуль упругости E=11850 МПа, коэффициент Пуассона ν=0,113; для раствора E=4600 МПа, ν=0,23. А для каменной кладки в гомогенной модели – на основе использованных в [42]: E=3680 МПа, ν=0,2.

Construction of Unique Buildings and Structures, 2016, №11 (50)

Рисунок 2. Конечно-элементные схемы сводов. Сверху сплошные модели, снизу конструкции «кирпич плюс раствор».

По результатам расчета (табл. 2) напряженное состояние сводов в упрощенной и подробной расчетных схемах в целом оказалось сходным (рис. 3). Максимальные значения (без учета скачков в опорных пятах) главных сжимающих и растягивающих напряжений в гетерогенной модели были значительно выше, чем в гомогенной. Причем при увеличении стрелы подъема разрыв увеличивался все больше: от 10-20 % разницы для высоты 0,5 м до двукратного превышения при высоте 1,5 м. Это объясняется перераспределением напряжений между кирпичами и растворным швом, а также неравномерным распределением напряжений в каждом отдельном кирпиче (рис. 4, 5). Напряжения в растворных швах оказываются значительно ниже, чем в кирпиче и распределены равномерно. Вертикальные швы оказываются наименее нагруженными, величина напряжений в них достигает не более 30-40% от максимальных значений для данной зоны. Напряжения в швах постели достигают 70-80%.

Таблица 2. Результаты расчета

№ п/п	Используемая модель	Стрела подъема, м	Время расчета, c	Максимальные главные растягивающие напряжения, МПа	Максимальные главные сжимающие напряжения, МПа	Максимальные касательные напряжения, МПа
1	Гомогенная	0,5	39	-	-0,071	0,035
2		1	43	0,018	-0,08	0,047
3		1,5	58	0,09	-0,12	0,054
4	Гетерогенная	0,5	299	-	-0,103	0,038
5		1	341	0,019	-0,145	0,051
6		1,5	376	0,132	-0,236	0,07

Construction of Unique Buildings and Structures, 2016, №11 (50)

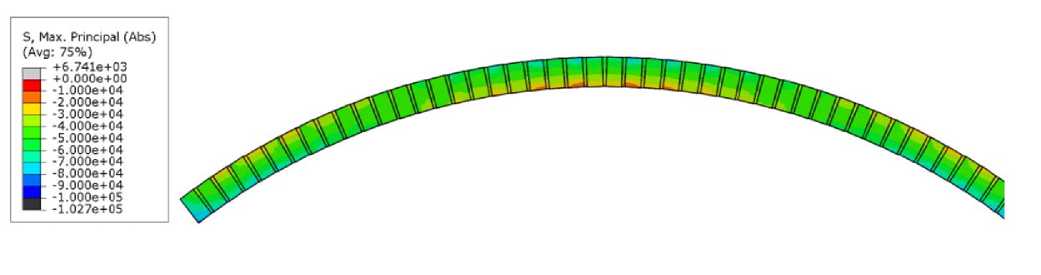
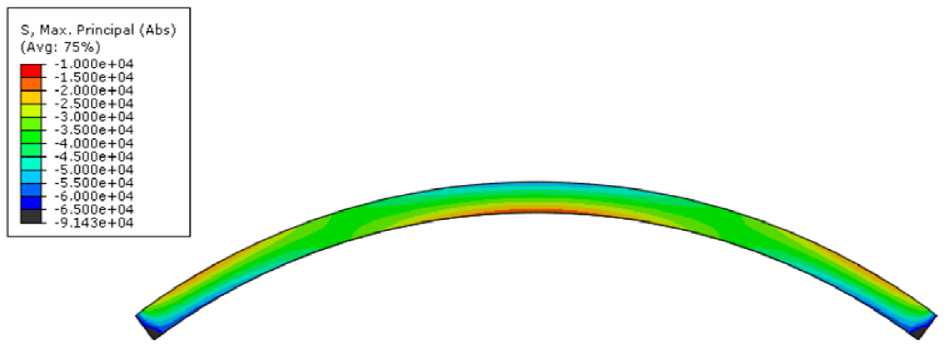
Рисунок 3. Гетерогенная и гомогенная модели свода со стрелой подъема 0,5 м. Максимальные главные напряжения, действующие в сечении

Стрела подъема не напрямую влияет на интенсивность напряжений и их распределение. Величина напряжений зависит главным образом от объема вышележащей кладки, а распределение – от отношения стрелы подъема к пролету свода.

На кирпич во всех случаях передаются более высокие напряжения, кроме того, они распределены неравномерно. Напряжения концентрируются по угловым зонам, а также по полосам, параллельным вертикальным растворным швам. Такое распределение характерно и для сжимающих и для растягивающих напряжений.

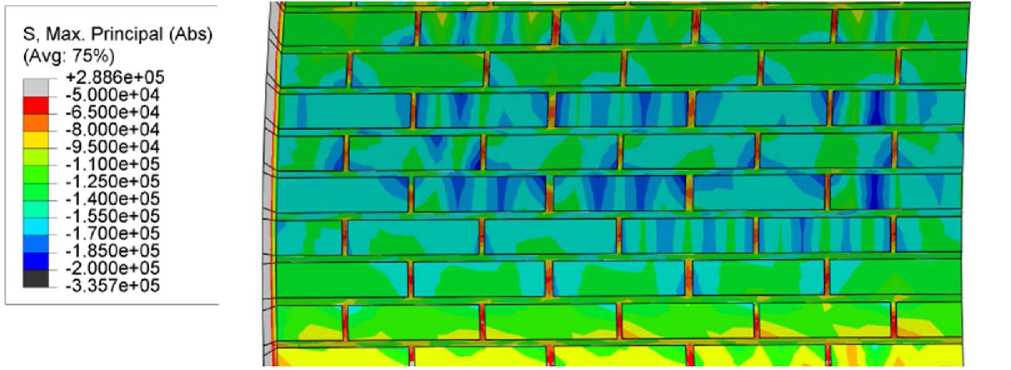
Рисунок 4. Свод со стрелой подъема 1,5 м. Распределение главных сжимающих напряжений на нижней поверхности свода в сжатой зоне

Construction of Unique Buildings and Structures, 2016, №11 (50)

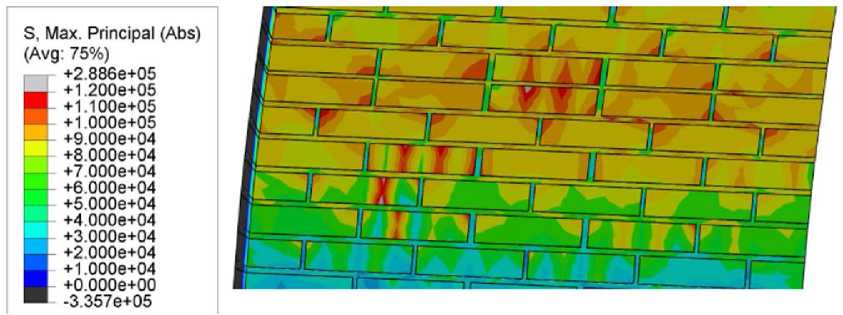
Рисунок 5. Свод со стрелой подъема 1,5 м. Распределение главных растягивающих напряжений на нижней поверхности свода в зоне шелыги

Также можно наметить разницу в характере напряженного состояния кирпича и растворных швов. Растворные швы постели (рис. 6) в сжатой зоне находятся в состоянии всестороннего сжатия, так как второе и третье главные напряжения сравнимы по величине с первым, а в растянутой зоне – в состоянии всестороннего растяжения. Кирпичи же находятся в состоянии простого линейного внецентренного сжатия, и существенным является только одно из главных напряжений (рис. 7). Это дает основания полагать, что в сжатой зоне свода сначала происходит разрушение кирпича, а затем раствора – при потере состояния трехосного сжатия, а в растянутой зоне сначала происходит разрушение раствора.

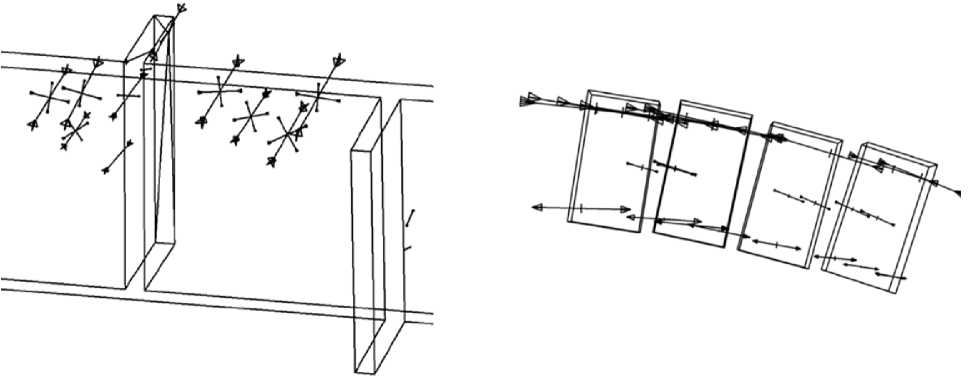
Рисунок 6. Линии действия напряжений в растворных швах свода

Рисунок 7. Линии действия напряжений в кирпичах свода

По полученным данным можно сделать вывод о пригодности гетерогенной модели для полноценного анализа прочности кирпичных сводов по допускаемым напряжениям, даже без задания сложного взаимодействия между кирпичом и раствором, как это предложено P.B. Lourenco, поскольку в случае конструкции, как правило, не стоит задача определения механики разрушения и закритической работы. Однако видно и то, что расчет таких моделей занимает в 8-10 раз больше времени и ресурсов. Также данная модель представляет собой наиболее простой случай свода, в то время как реальные конструкции сложнее в построении и требуют больше ресурсов.

Для определения прочностных и деформационных характеристик кладки рациональным представляется моделирование испытаний образцов кладки по тому же принципу, что и представленное гетерогенное моделирование сводов. В соответствии с моделью P.B. Lourenco для этого необходимо будет задавать прочностные характеристики кирпича и раствора. Что же касается дополнительных плоских элементов, определяющих контактные свойства, предполагается задавать вместо них непосредственное взаимодействие между кирпичами и раствором через прочность нормального и касательного сцепления.

Construction of Unique Buildings and Structures, 2016, №11 (50)

5.    Заключение

Исходя из рассмотренных исследований, можно сформулировать основные задачи, решение которых необходимо для формирования универсальной прочностной модели кладки, которая бы подходила и для криволинейных конструкций сводов:

• 1)    На основе критерия Г.А. Гениева для плоского напряженного состояния разработать модифицированный критерий для объемной постановки задачи.

• 2)    Для исключения необходимости проведения множественных прочностных испытаний кладки различных форм, разработать способ виртуальных испытаний. Он должен обеспечить автоматизированное проведение серии тестов конечно-элементной модели кладки необходимой конфигурации и получение всех необходимых характеристик для подстановки в критерий Г.А. Гениева, или иной критерий с достаточной сходимостью результатов. Исходными данными остаются только прочностные характеристики кирпича и раствора, которые либо известны, либо их получение не составляет существенных трудностей. Обязательным требованием к данной модели испытаний должна стать высокая сходимость результатов с испытаниями реальных образцов.

Альтернативным подходом может стать рассмотренное в статье подробное моделирование кладки сводов, как сложной конструкции «кирпич плюс раствор». Такое моделирование допустимо, если есть возможность достаточной автоматизации в построении модели, либо при встраивании гетерогенного участка непосредственно в гомогенную модель. Исходными данными также будут прочностные характеристики кирпича и раствора. Такая модель показывает участки предельных состояний сразу на элементах конструкции. Главные недостатки здесь – это сложность построения модели и ресурсоемкость, а так же высокие требования к качеству конечно-элементной сетки.

Таким образом, наилучшим решением представляется модель, содержащая следующий алгоритм действий:

• •    Находятся компоненты уравнений модифицированного критерия Г.А. Гениева по результатам серии виртуальных испытаний образцов кладки;

• •    Напряжения в конструкции определяются из ее сплошной изотропной конечно-элементной модели;

• •    Прочность ключевых зон конструкции определяется подстановкой действующих в них напряжений в модифицированный критерий Г.А. Гениева.