Продольные колебания слоистых и структурно неоднородных композиционных стержней

DOI:

В статьях [5; 6] разработана методика решения статических задач для одноосной деформации композиционных стержней. Она успешно применена в перечисленных работах при создании обобщенной модели Винклера деформируемого слоя на случай присутствия неоднородностей и включений в его материале.

В связи с успешностью проведения указанных исследований и общеизвестностью вывода уравнения продольного колебания однородного линейно упругого стержня [1] возникла необходимость применить разработанный авторами подход [5; 6] для построения эффективных свойств среды при решении динамических задач, в частности, для композиционных линейно и нелинейно упругих стержней, а также стержней, обладающих реологическими свойствами.

Под стержнем будем понимать твердое тело призматической формы постоянного квадратного поперечного сечения площадью S и длиной X [1]. Будем считать, что стержень расположен вдоль оси 0 x (рис. 1). Для определенности направим ось 0 y вверх. Кроме того, не ограничивая общности, будем считать, что одна из граней параллельна плоскости x 0 y . Будем считать, что внешняя нагрузка (а x ), приложенная к сечению, является равномерно распределенной по S в любой точке стержня x е [ 0, X ] , ее главный вектор T = (а x) • S (интегральные значения нагрузки по сечению) действует вдоль оси 0 x . Пусть смещение любого вертикального сечения в точке x е [ 0, X ] в момент времени t будет характеризоваться функцией u ( x , t ). Известно, что относительное удлинение (е x ^ (деформация) стержня в любой точке x определяется дифференциальным равен- д u ( x , t ) ством е x =         [1].

д x

АУ

Рис. 1. Стержень квадратного сечения

Исходя из того что одномерное уравнение состояния композиционного стержня для его элемента длиной не меньшей, чем X'<определяется уравнением (аx) = з((е_x)), можно записать, что разница сил ΔT, приложенных в точках х₁ и х₂, равна [1]:

^fd u ( x ₂, t ) )      / a и ( x i , t )

Д T = ^д I             I • S - ^д I ----:-----

д x

д x

• S =? d sf^ L =

J I дx x1

x 2^ ,(ди ( x , t ) )д² и ( x , t )

= д I            I dx • S ,

I     дx     I д x ²

x ₁

d 3 ( e )

где д ( e ) = ——. В (1) очевидно предполагается, что X < ( x ₂ - x ,) .

dε                                                                ^{2    1}

n

Пусть (р) = ^ у k ■ р _к - средняя плотность материала стержня на интервале X', где р _к - плотность к -й компоненты композиционного материала, а у к - ее объемная доля. Тогда вертикальная инерционная составляющая рассматриваемого участка стержня определяется формулой [1]:

x.2 f    .2, Л j {р)— dx • S, JI      at2 J

x ₁

X

7

где S – площадь поперечного сечения стержня.

Пусть на каждую компоненту материала композиционного стержня действуют внешние силы с плотностью g_k ( x , t ) (действующей на единицу массы k -й компоненты композиционного материала), тогда к интегралу сил, действующих на интервале ( x ₁, x ₂), следует добавить силу:

x ₂

j gg (x, t) ddx • S, x1

n где gg(x,t)) = £yк -Pk • gk (x,t).

Исходя из баланса действующих сил, получаем, что инерционные силы должны быть скомпенсированы внешними и внутренними силами, тогда из (1)–(3) получаем:

x _{2           2}                 x ₂

S№ | dx • S = J ^

x ₁

x ₁

д u(x , t ) ^5² u(x , t)          ^x 2, , ..

—(-^7     (-^^ dx • S + [ gg ( x , t )) dx • S .

д x Id x^{2        J  v} "

x ₁

Уравнение (4) можно переписать в виде:

^{x 2 f}, _хд² и       д и ( x , t ) ^д² и ( x , t )

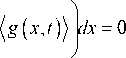
^j I/² "57     I д x J д x²

^x i X                 X            7

Если считать, что участок стержня ( x ₁, x ₂) настолько мал по сравнению с длиной волны, что выполнена формула Лагранжа [3]:

x 2           2

r I , x д и jI P 5t2"- x i X

д и ( x , t ) |д² и ( x , t ) д x J д x²

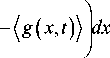
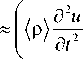
‘I д и ( x , t ) |д² и ( x , t ) I    д x    J   д x²

-

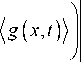
• ( ^x 2 - ^x i ) ,

^x = ^x 0

где x 0 e ( x 1 , x ₂ ) - некоторая точка, то из (6) с очевидностью будет следовать локальное уравнение колебания стержня:

д² и д t²

д и ( x , t ) ^

д x   )д² и ( x , t ) gg ( x , t )^

( р)         ^{д x 2}          (p)

Отметим, что в случае, когда 3' ( е ) представляет собой константу, то есть, например, в случае линейного однородного материала, сложный коэффициент приобретает общеизвестный вид [1]:

d u ( x , t ) ^

a x   7 e ₂

(р)      = р = .

Применить метод Фурье к решению (7) для произвольной функции 3 ( ) не представляется возможным. В этом случае его решение будет требовать применения универсальных численных методов, например разностного, и соответственно получить аналитические зависимости влияния неоднородностей на собственные частоты колебаний стержня будет невозможно.

Самым простым способом решения поставленной задачи является установление связи средней деформации стержня (е x ^ = u ⁽ x ’ t ) с его средним напряжением (с x ).

В соответствии с общей методикой, примененной для решения задачи определения эффективных параметров стержня, рассматривается элемент композиционного материала (макроточка), на границе которого задаются воздействия, имитирующие воздействия, возникающие в стержне, то есть в данном случае рассматривается растяжение/сжатие призматического стержня на участке к' [6].

Принцип реализации метода гомогенизации для призматического стержня квадратного сечения заключается в следующем: если армированный материал состоит из N компонент (фаз) и в среднем изотропен (например, имеет место хаотическое армирование и т. п.), то можно использовать гипотезу Фойгта для призматического стержня о том, что в простейших опытах на чистое растяжение/сжатие предполагается, что деформации по всему объему композиционного материала призматического стержня постоянны. Второй предельный случай (гипотеза Рейсса) заключается в том, что в тех же простейших экспериментах на растяжение предполагается, что напряжения по всему объему композиционного материала призматического стержня в среднем постоянны.

Полученные на основании этих гипотез формулы имеют практическую ценность, так как являются соответственно верхней и нижней оценкой истинных модулей композиционного материала [6].

Рассмотрим линейно-деформируемый композиционный структурно неоднородный материал элемента стержня к' из n линейно-деформируемых компонент с модулями упругости Е_к и объемными долями у _к . Тогда напряжение натяжения (a x ) в (8) определяется по заданной средней деформации элемента стержня ^е x ) [6]:

где nn

I У Yr E IT—

1 + к ExL =-

I Д^ Ik ^k I Д^ 771

V k =1 7 k =1 E k

2 • У Ya. £ 1 E k

.

N

Отметим, что если вместо Ex_x}_x взять усреднение по Фойгту Ех_хф_ф = ^у _k ■ Ek [6], то (8) даст решение для упругого продольно слоистого стержня, а если взять усреднение по Рейссу

Р

^y 2L ^ Ek к к =1 ^к.

Л-1

, то (8) будет физически эквивалентно решению динамической задачи усред-

У

нения для поперечно слоистого стержня.

Используя метод Фурье [1] для решения уравнения свободных колебаний (( g ( х , t )) = 0 в (7)), можно получить формулу для определения собственных частот колебания продольно слоистых,

поперечно слоистых стержней и композиционных структурно неоднородных стержней (рис. 2):

го пр. с.

i - п

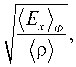
поп.с.

го .

i-п к Е х^Р X \ (р)

комп.

, ^го i

i ^-п к E x L ^X \ (р)

( i = 1 ,N ).

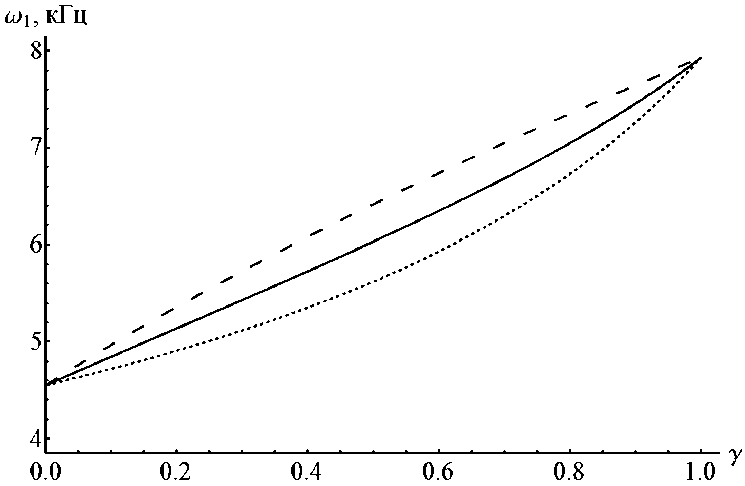
Рис. 2. Зависимость низшей собственной частоты го Пр ^с. продольно слоистого (штрихпунктирная линия), го попс поперечно слоистого (пунктирная линия) и го Комп композиционного структурно неоднородного (непрерывная линия) стержней длиной X = 1 м от концентрации у первого материала в двухкомпонентной смеси ( Е 1 = 2 - 10¹¹ Па; Е ₂ = 0,7 - 10”Па; р = 7850 кг/м³; р ₂ = 8330 кг/м³ )

Из условия наличия неоднородностей в материале стержня в соответствии с характером вывода уравнения (1)–(4) можно утверждать, что количеством N достоверно вычисленных частот (9) для композиционного стержня является значение, удовлетворяющее неравенству:

X v — >> X

N ,

X то есть длина волны N должна быть больше размера неоднородности минимум в 10 раз.

В этом случае можно получить затухание собственных частот со временем, обусловленное внутренним трением в материале. Будем использовать наследственную теорию ползучести. В рамках этой теории будем использовать уравнения релаксации вязкоупругого однородно стареющего материала с ядром релаксации R ( t , τ) и мгновенным модулем упругости E ( t ) [2; 5]:

t

о х ( t ) = ^Е ( t ) ^-l ^s х ( t ) ^- j s х ( ^т ) ^- R x ( t ,^т ) d ^т к          0

В этом случае (1) можно записать для Δ T ( t ):

A T = E (t )•

d u ⁽ x i , t ) rd u ⁽ x i ,T )

dx     J

к            0

d x

к

• R x ^{( t ,t )} d T • ⁵

J

—

— E (t )•

к

du (x 2, t) r du (x 2,t) dx      J

x ₂

= E (t )• Jd

x ₁

x ₂

=E (t )-J

d u ( x , t )

к   dx

t

—J

d x

^Лд ² u ( x , t )

x к

d x ²

—J'

d u ( x , t ) d x

d ² u ( x , t ) d x²

• • R x ^{( t ,t ) d T} • ⁵ =

J

^

• -    • R x ( t , t ) d t • 5 =

J

к

• -    R ( t , t ) d t dx • 5.

J

Действуя далее аналогично (2)–(6) с использованием (22), получаем уравнение продольного колебания стержня с учетом реологии однородного материала:

d ² u = E ( t )   d ² u ( x,t)

d t ²     P

•

d x ² к

—

Г d 2 u ( x,t )/

J я 2    R ^{x ( t,T} d^T

+ g ^{( x,t} ) ^ρ

.

Отметим, что при использовании нелинейного уравнения релаксации стержня [4]:

t

°x (t) = 3(£x (t)) —J3(£x (T)) •Rx (t,T)dT совершенно аналогично (23) можно получить уравнение:

d² u d t²

L,/du (x, t )k 3'1                 I к dx J

P

d2u (x, t) • dx

, к d u ( x, t)A

³ '|                I „2

r I    d x     I d² u(x , t) „ , _x ,

— J—------^Z— Rx ( t , t) ^d T

0 P         d x

g (x, t)

P

к                                                            J

Рассмотрим продольно слоистый стержень длиной X из n различных материалов с собственными значениями мгновенного модуля упругости E_k ( t ) и ядрами релаксации R_{x , k} ( t , τ), будем предполагать, что для пакета выполнена гипотеза Фойгта о равенстве для всех слоев их деформаций, тогда для каждого из слоев получаем напряжение:

к,                                                            к

° x , k ( x , t ) = E k ( t ) • k^£ x ( x , t )) ^— j (^£ x ( x , ^t)) • R x , k ( t , ^t ) d ^t I .

к              0                          J

Домножая на объемные доли у _к и суммируя по к = 1, n (25), слева получаем среднестатистическое значение напряжения в смысле дискретной случайной величины, распределение которой определяется у _к :

кк

(стx(x,t= (E(t))Ф -I ^£x(x,t)) — J(£x(x,T^\Rx (t,t)фф dT I к0                            J где

nn

(° x ( x , t )) = S y k • ° x , k ( x , t ) , E ( t )) Ф = S y k • E k ( t ) , ( R x ⁽ t ,т )) Ф = k =1                                              k =1

1 ⁿ

(E ^" s y k • E k ⁽ t ) • R x , k ⁽ t ,^{т )} .

Перейдем к рассмотрению поперечно слоистого стержня длиной X из n различных материалов с собственными значениями мгновенного модуля упругости E_k ( t ) и ядрами релаксации R_{x , k} ( t , τ), будем предполагать, что для пакета выполнена гипотеза Рейсса о равенстве для всех слоев их напряжений, тогда для каждого из слоев получаем напряжение:

( ° x ⁽ x , t ^

Ek (t)

t

^S x , k ( x , t ) — J ^S x , k ( x , ^ТУ ^R x , k ( t , ^T ) d ^T I .

0                             7

Предположим в (26), что e _x k ( x , t ) = y _k -(e _x ( x , t )} , где (e x ( x , t )) - средняя деформация пакета, домножая (26) на у _к и суммируя по k = 1, n , получаем:

Г,1

( ° x ( x, t )S (E ( t )) Р -I (e x ( x, t ^-J^ x ( x, T)H Rx (t, ^ Pd T| ,

V             0

zx -1

Г1

где ( ^{E (} t )) Р = | S утл I , ( R x ⁽ t , ^т)) Р = S y k • ^R . ⁽ t , ^т) .

V k=1 Ek ( t )7

Таким образом, если при выводе (25) и (27) рассматривать элемент стержня длиной X' с использованием стандартной методики усреднения [5], можно получить для структурно неодно- родного композиционного материала одноосно нагруженного стержня следующую связь между напряжениями и деформациями:

Г,                                                     1

(° x ^{( x} , t ^ = ( ^{E (} t )) _% • Ц^е x ^{( x} , t )) ^- J 7 x ⁽ x , ^т)) • ( R x ⁽ t , ^т)) _% d ^т I ,

V               0                               7

где nn

^{1 +} | S y k • E k ⁽ t ⁾]- S

(^E ( t )) ,

V k =1 ______________ 7 k =1 ^E k ( t )

2 •S k"1 Ek (t)

(^Rx ⁽ t , ^т)) Z =

S Y k -E , ( t ) • R. , k ( t ,r ) + ( E ( t )) p ■£ Y k-- R . , k ( t ,т ) k =1 _____________________________________________________ k =1 ________________________

7 E ( t ,

Используя усредненные коэффициенты уравнений (25), (27), (28), по аналогии с результатами (21)–(24) можно получить уравнения затухающих колебаний для продольно слоистого, поперечно слоистого и структурно неоднородного композиционного стержня:

d 2 u d t 2 "	(E ( t )) ф (P)	Гd 2 u ( x , t ) V d xx	- J d 0	12 u ( x , т ) d xx	(Rx ( t ,т )	) d т Ф	L дЫ 7 (p) ,
d 2 u	(E ( t )) p I	г d 2 u ( x , t )	- J -0	u ( x , т )	: Rx ( t ,т)>	d т p 7	(g ( x , t )) ( p)
d t 2	(p>     I	V 5 x 2		d x x
d2 u = 1 d t 2 =	E ( t )L .1 (p)     1	Гу 2 u ( x , t ) V 5 x 2	J - 0	u ( x , т ) , d xx '	R x ( t ,<	d т	(g ( x , t )) ( p)

,

Количество N достоверно вычисленных частот для композиционного стержня определяется неравенством:

X

>>

N

X'

.

Возможно более интересные (аналитически обозримые) результаты по сравнению с непосредственным решением уравнений (23) можно получить с использованием простейших соотношений теории ползучести по теории старения [7]. В частности, предположить, что уравнение релаксации имеет вид:

ст , ( x , t ) = E -e x ( x ) -^ ( t ) ,

где E - модуль упругости стержня; T ( t ) - функция релаксации, в частности, ¥ ( t ) = коэффициенты а и р зависят от температуры [7].

1 + а - t ^в

где

В этом случае уравнение (23) приобретет вид:

д 2 u = E д² u ( x , t )      t ) + g ( x , t )

д t ²   p    д x ²               p

.

Соответственно из (30) можно получить угасающие собственные частоты для однородного стержня (рис. 3):

i -n E

Ю( t 1    ; \ ,/T( t).

X p

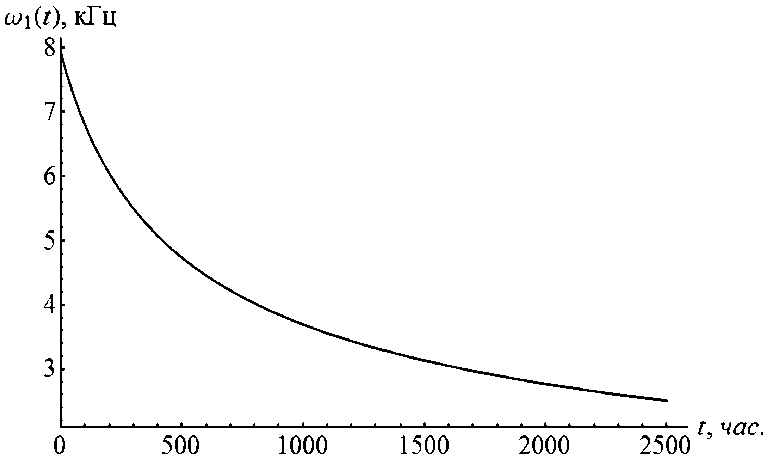
Рис. 3. Зависимость низшей собственной частоты ю 1 ( t ) стержня длиной X = 1 м от времени t ( E = 0,7 • 10¹¹; р = 8330 кг/м³ и функцией релаксации Малинина [7] в виде ^ ( t ) = 1] ( 1 +10 ^{- 6} - 1 ) )

Совершенно элементарно выглядят обобщения (30) и (31) при получении затухания собственных частот для продольно слоистого стержня юПр. с.(^t) (гипотеза Фойгта), поперечно слоис- того стержня mПопс (t) (гипотеза Рейсса) и структурно неоднородного композиционного стержня m комп. (t) (гипотеза Хилла):

m П t )= ^ ^'/ И t)) ф , m ТЧ t ) = i^ P^ ^-t t)) p, m Км (t ) = ^ ^Д^ -t t)) x (i = 1, N M32> nn

1 n                          „                       E y k • Ek •( k ( t И E xX E y k ² •- k ( t )

^{где -}l t )) Ф = T^vEy k • E k -⁽ k ⁽ t ) , Ф⁽ t )) P = E y k ² -⁽ k ⁽ t ) , ^-i t )) x =  ------------ x,-—----------- , y k ,

^Ех)ф i = l                                    i =l                                                   2\ ^Exlx

E k , , — k ( t ) — концентрация, модуль упругости, функция релаксации k -й компоненты композиционного материала ( k = 1, n ), ( Е ф , фф, ( Е ф - средние значения модулей упругости по Фойгту, Рейссу и Хиллу, определяемые соотношениями, приведенными в абзаце после уравнения (8).

При использовании нелинейного уравнения релаксации по теории старения [7]

□ x ( x , t ) = 3 ( s x ( x ) ) - ^— ( t )

несложно обобщить уравнение (7) до уравнения, содержащего функцию релаксации

,fd u ( x , t ) )

^ I                I d2u =   I dx J 5 u (x, t)          (g(x, t))

d t ² =      (p)         d x²    ' ⁽⁾      (p)

Методика получения нелинейной функции 3 ( ) гомогенизированного n -компонентного слоистого или структурно неоднородного композиционного упругого стержня в случае применения билинейной диаграммы Прандтля или степенной функции для описания деформирования каждой из компонент изложена в работе авторов [6] для деформирования без разгрузки упруго-пластических и гиперэластичных материалов. Так как в данной статье рассматривается только упругая деформация стержня, то есть особенности разгрузки отсутствуют, то результаты [6] могут быть перенесены на этот случай с точностью до замены названий констант. При этом будет неявно использоваться гипотеза о том, что растяжение/сжатие нелинейно упругого материала стержня 3 ( ) центрально симметрично относительно начала координат.

Одним из наиболее распространенных способов решения задач реологии является использование нелинейного релаксационного уравнения Фойгта [8], являющееся физическим аналогом параллельно закрепленных двух нелинейных упругого и вязкого элемента:

.

• □ = 3 ( e ) + E| £ I ,

где 3 ( ) - как и раньше монотонно возрастающая функция, описывающая растяжение/сжатие z                                      d 3

первого упругого элемента (в линейном случае, как всегда, 3 = — = Е - модуль упругости); dε

В ( ) - монотонно возрастающая функция вязкости второго вязкого элемента (в линейном случае

,,     d В

f Д ⁿ                           x . d£ d u

.

d I _s I - вязкость материала); £ = — =---

Г J                                    d t d t d x

Опуская повторение очевидных преобразований (22), получаем общее уравнение однородного нелинейно-вязкоупругого стержня по модели Фойгта:

,f du (x, t )^             „,f du (x, t )Y d2u      ( dx J d2u (x, t)     ^   dx   J d3u (x, t) g (x, t)

d t ²          p         d x ²             p        d t d x ²        p

При использовании гипотезы о равенстве скоростей деформаций всех компонент композиционного материала в пакете из n различных компонент в случае использования линейной модели в обоих деформируемых элементах для каждого материала с номером к ( 3 k = E k , 5 _к = n _к ) несложно из (34) получить следующие усредненные уравнения для продольно слоистого, поперечно слоистого и структурно-неоднородного композиционного материала:

..                                                                                                                                                                           .

c = ^Фф 's + Wф s, о = ^P, • £ + (n)p s, ° = E^x • s + (n)x s, где E Ф , E Р, E Х определены в абзаце после уравнения (8),

(И ф ⁺W p )

nn

(ПфФ = Z Yк -Пк, Ыp = EPF £ Yk •   , (n)x = к=1                             к=1      Ek

Используя (36) по аналогии с (35), легко получить реологические уравнения продольных колебаний композиционного стержня по линейной модели Фойгта. Например, для структурнонеоднородного композиционного стержня получаем:

d ² u = EX d ² u ( x , t )   (n) _x d ³ u ( x , t )   gg ( x , t )}

d t²     (p) d x ²        (p) d t d x ²         (p)

В (37), как всегда, длина структурного элемента Y ' мала по сравнению с размерами стержня X .

Отметим, что в случае нелинейных функций 3 к ( ) и ⁵ _к ( ) , описываемых степенной функцией или диаграммой Прандтля для каждого к ( к = 1, n ), необходимо также воспользоваться методикой работы [6].

Получены уравнения продольных колебаний стержня для всевозможных комбинаций линейно упругих и реологических свойств как однородных стержней, так и продольно слоистых, поперечно слоистых и структурно-неоднородных композиционных стержней с использованием приближения Хилла для эффективных свойств стержня.

Использованы следующие реологические модели: уравнения линейной или нелинейной релаксации по наследственной теории (в линейном случае со старением), технической теории старения, нелинейное и линейное уравнение релаксации Фойгта.

В некоторых случаях получены аналитические выражения для собственных частот колебания композиционных стержней.

Получены уравнения продольных колебаний однородных нелинейно упругих стержней, указан метод обобщения этих уравнений на случай композиционных материалов с учетом реологии поведения материала.