Продолжение семейств симметричных периодических решений гамильтоновых систем через точки соударения
Автор: Батхина Н.В., Батхин А.Б.
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Прикладная математика
Статья в выпуске: 8, 2004 года.
Бесплатный доступ
Предлагается адаптивный высокоточный алгоритм продолжения симметричных периодических решений гамильтоновых систем. В основе алгоритма лежит методика исследования структуры семейств периодических решений, предложенная Б.Б. Крейсманом. Этот алгоритм отличает высокая точность, экономия компьютерных ресурсов, возможность распараллеливания. Он позволяет проходить ударные орбиты, оставаясь в физических координатах. Используя адаптивный алгоритм, авторы исследовали семейства ударных периодических решений второго рода плоской задачи Хилла, имеющие некоторые симметрии.
Короткий адрес: https://sciup.org/14968553
IDR: 14968553 | УДК: 517.933:521.1
Текст научной статьи Продолжение семейств симметричных периодических решений гамильтоновых систем через точки соударения
Существенную роль при изучении динамики в гамильтоновых системах играют периодические решения. В отличие от диссипативных систем, для гамильтоновых характерно всюду плотное существование периодических орбит, правда с большими периодами. При наличии первых интегралов в системе эти решения объединяются в семейства. Следуя Анри Пуанкаре, среди этих семейств выделяются семейства периодических решений первого рода, которые можно рассматривать как порождающие. Устойчивые периодические решения с периодом Т при определенных условиях могут «порождать» периодические решения с периодом с[Г. Их принято называть периодическими решениями второго рода. Если среди них есть устойчивые, то они так же могут быть порождающими, и т. д. Для гамильтоновых систем, для которых число первых инволютивных интегралов меньше числа степеней свободы, возникают ситуации, когда такое ветвление может продолжаться бесконечно. Такое поведение принято называть «динамическим хаосом», а обнаружение таких явлений вполне может рассматриваться как доказательство неинтегрируемости системы. Такой подход к изучению семейств периодических решений позволяет провести их классификацию и установить генетическую связь между различными периодическими решениями.
Большая часть методов продолжения периодических решений разработана для диссипативных систем. Эти методы, во-первых, не могут быть непосредственно применены к гамильтоновым системам, а, во-вторых, совершенно не используют их характерные свойства. В серии работ Б.Б. Крейсмана, основанных на ранних работах А.Д. Брюно, показано, что вся информация о структуре семейства периодических решений содержится в матрице монодромии, соответствующей этому решению. Помимо такой важной характеристики, как индекс устойчивости, матрица монодромии в линейном приближении задает направление продолжения семейства периодического решения в фазовом пространстве и изменение его периода, позволяет определить индикаторы бифуркаций решения. Достаточно полная теория была построена для гамильтоновых систем с двумя степенями свободы. Эти результаты позволяют построить эффективные алгоритмы продолжения семейств периодических решений.
Основным источником гамильтоновых систем служат небесно-механические задачи. Однако гамильтонианы таких задач содержат особенности вида 1/г”, и в процессе продолжения семейства возможны ситуации, когда решение начинает приближаться к особой точке и становится ударным. Такие решения имеют практическую ценность, поскольку любая траектория космического аппарата с той или иной точностью является ударной орбитой. С другой стороны, продолжение семейства через соударение интересно и с той точки зрения, что позволяет перейти к орбитам с другими топологическими и динамическими свойствами, которые могут быть использованы, например, для гравитационного маневра космического аппарата.
В данной работе рассматривается теория продолжения семейств периодических решений гамильтоновых систем с двумя степенями свободы, обладающих симметриями. Применение локальной регуляризации позволяет продолжать семейства периодических решений через особые точки. Реализованы алгоритмы, существенно использующие симметрии гамильтоновой системы. Данные алгоритмы применены к симметричным семействам плоской задачи Хилла, обладающей двумя симметриями.
1. Метод продолжения семейств симметричных периодических решений
Пусть дана автономная гамильтонова система с п степенями свободы, заданная гамильтонианом Н(х), х £ R2". (Везде далее для определенности будем полагать, что п = 2.) Тогда ее динамика описывается каноническими уравнениями где х — 2п-мерный вектор координат и импульсов, J — симплектическая единица. И пусть известно некоторое решение этой системы
x(t) = X0(t), которое будем называть порождающим, и в окрестности которого функция Гамильтона является достаточно регулярной. Рассмотрим возмущенное движение х^ = х0(£) +y(t).
Подставляя его в уравнение (1), разлагая правые части в ряд Тейлора по у^) и отбрасывая члены разложения степени выше первой, получаем уравнения возмущенного движения в первом приближении
$ = ЛНез8(Я(хоМ))у. (2)
at
Это уравнение называют уравнением в вариациях Пуанкаре.
Пусть известно решение системы (1), зависящее от произвольной постоянной x(t) = х^су и порождающему решению соответствует С = 0. В этом случае уравнение в вариациях (2) имеет частное решение
_ dx^t, С)
У| “ дС ’ где все частные производные вычислены в точке С = 0. В частности, автономная система вместе с решением x(f) = x0(i) имеет решение x(t) = x0(t + С), т. к. это просто сдвиг вдоль траектории. Ему соответствует решение уравнения в вариациях У1 = JVH(x0(t^.
Если система (1) имеет первый интеграл F(x) = const, то и уравнения в вариациях также имеют первый интеграл (VF(x0(^),y) = const и частное решение у = JVF(x0(£)), совпадающее с решением у2 = JV Н (x0(t)).
Система уравнений в вариациях является линейной системой с переменными коэффициентами, поэтому ее решение представимо в виде y(t) = Y(t)y0, где У о = у(0). Матрицант Y(t) для гамильтоновых систем является симплектической матрицей.
Матрица М = Y(T), равная значению матрицанта в конце периода, называется матрицей монодромии, а ее собственные значения рк — мультипликаторами системы (2). Очевидно, что
Y^ + Т) = Y(t)M.
Подставим в последнее равенство значение t = —Т/2, получим
Y(T/2) = Y(—Т/2)М, откуда
М = Y”1(-T/2)Y(T/2). (3)
Матрица монодромии вещественна, поэтому вместе с мультипликатором р она имеет комплексно-сопряженный мультипликатор р. Для га.мильтоновой системы наряду с мультипликатором р матрица монодромии имеет обратный мультипликатор 1/р. Поэтому у вещественных гамильтоновых систем мультипликаторы образуют четверки (р, р, 1/р, 1(р\ или, по крайней мере, пары (р, 1/ р), располагающиеся либо на вещественной оси, либо на единичной окружности комплексной плоскости.
Конкретный вид матрицы монодромии зависит от выбора начальной точки на порождающем решении, но значения мультипликаторов и структура матрицы М инвариантны относительно сдвига вдоль решения и невырожденных преобразований фазового пространства.
Для вычисления матрицы монодромии обычно приходится интегрировать на интервале времени [О, Т] совместно уравнения движения и уравнения в вариациях Пуанкаре для единичной матрицы начальных условий, то есть решать численно задачу Коши для системы уравнений порядка 2п(1 + 2п). Однако вычисление матрицы монодромии можно существенно упростить, если гамильтониан допускает некоторые симметрии.
Не умаляя общности, предположим, что гамильтониан инвариантен относительно канонической замены переменных
(а?1,Х2,^3,^4) (^1, -^2,-^3,^4), t-*(-t\ (4)
Для симметричной относительно оси х4 периодической орбиты можно выбрать начальную точку х(0) = (ti, 0,0, х4\ в которой траектория ортогонально пересекает ось симметрии. Тогда будут выполнены условия:
Т1(™^ = Ху^, х2(-^ = -я2(<), ^3(-t) = "X^tY, x^-t^ = x4(t\ (5)
Более того, в момент времени t — Т/2 вновь будет выполнено условие ортогональности х(Т/2) = (т'р 0,0, x'4Y
Инвариантность гамильтониана относительно преобразования (4) означает, что он является четной функцией относительно переменных х2 и х^, а значит, вдоль симметричных относительно оси хг орбит гессианы гамильтониана в моменты времени t и — t будут связаны соотношением:
{—H/^x^Y только один из индексов ij принимает значение 2 или 3; (6)
Я"(х(£)). во всех других случаях.
Эти условия равносильны матричному тождеству
Hess H(x(-tY = JGJ Hess Я(х^))С”1, (7)
где матрица G имеет в силу замены (4) вид
G = Gi = diag{l, -1, -1,1}, причем Gf = Gr1 = Gp
Это означает, что для системы (2) выполнено условие t-инвариантности [4], а мат-рицанты Y(—t) и Y(t) для таких систем связаны уравнением
Y(-t) - G"1Y(t)G, в частности Y(-T/2) - G"1Y(T/2)G.
Так как матрица Y(—Т/2) симплектическая, то с учетом формулы (3) получаем матрицу монодромии Мь вычисленную от точки х(0),
Mi = G1YT(T/2)G1Y(T/2), где Gi = GiJ, Gf1 = Gf = Gb (8)
Нетрудно получить матрицу монодромии М2, вычисленную от точки х(Т/2),
М2 = Y(T/2)GiYt(T/2)Gi
Аналогичными рассуждениями могут быть получены формулы для вычисления матрицы монодромии в случае инвариантности гамильтониана относительно канонического преобразования
(а?!,ат2,ж3,ж4) —» (—371,ж2,37з, —ж4), t->(-t),(10)
для симметричных относительно оси х2 орбит,
М] =G2YnT/2)G2Y1(T/2),(11)
М2 = Y^T/2^G2Y^(T/2)G2.(12)
Здесь G2 = diag{—1,1,1, — 1}, G2 = G2J, G2 1 — G2 = G2.
Вычисление матрицы монодромии по формулам предпочтительнее по следующим соображениям. Во-первых, интегрирование системы (2) на половине периода требует меньших вычислительных затрат и дает более точные результаты. Во-вторых, для продолжения некоторых симметричных периодических решений требуется информация о структуре матрицы монодромии как в точке х(0), так и в точке х(Т/2).
Наконец, если гамильтониан обладает двумя симметриями, например, относительно осей а?1 и х2, то для вычисления матрицы монодромии достаточно знать матрицант системы (2) на четверти периода Y(T/4). Действительно, пусть начальная точка дважды симметричной орбиты расположена на оси х1; то есть имеет координаты х(0) = (гсц, 0,0, .тД, тогда координаты точки соответствующей четверти периода есть х(Т/4) = (0,х2,х3,0). Обозначим через Y^T/d) матрицант системы (2), соответствующий начальной точке х(0), а через Y2(T/4) — матрицант, соответствующий начальной точке х(Т/4). Согласно свойству матрицанта, имеем УДТ/2) = Y 2(Т /4)Yi(T'/4). С другой стороны, в силу свойства t-инвариантности уравнения в вариациях относительно преобразования (11)
Y2(-T/4) = G;XY2(T/4)G2 => Y2(T/4) = G2Y2(-7/4)G2 7
Используя тот факт, что Y2(—Т/4) = YfT(T/4) = —JYf(T/4)J, получаем для Y1(T/2) выражение
УДТ/2) =
Применяя t-инвариантность системы (2) относительно преобразования (4), в итоге получим формулы для матриц монодромии Mi и М2:
~12
М, — С,УГ(Т/4)С2¥1(774) ,(13)
г ~~ -12
М2 = Y1(T/4)G1Yr(T/4)G2 .
Пусть известно некоторое порождающее решение x(t) = x0(t) системы (1), и пусть оно периодическое с периодом Т, х0(Т) = хо(О). Для нахождения близкого к нему периодического решения х(£) = Xo(i) + y(t) с периодом Т + dT надо решить систему уравнений х0(Т + dT) + У(Т + dT) = хо(О) + у(0).
Для малых у, dT имеем необходимое условие
у(Т) + ^Л7Я(хо(О)) = О.
В силу уравнения в вариациях имеют решение yi = JVH(x0(t)) и первый интеграл С^Я(х0(^),у) = const. Выполним замену переменных у = Az с симплектической и одновременно ортогональной матрицей перехода А.
/ Я3 -Я4 Ят Я2 \
Я4 Яз Я2 -Я, -Нх -Н2 Н3 -Н4 ’ у—Я2 Ну н4 н3 / где Яь Я2, Яз, Н4 — компоненты нормированного вектора-градиента функции Гамильтона в начальный момент времени 1 = 0. Все рассматриваемые ниже матрицы — симплектические, если не оговорено противное.
Переменным z соответствует матрица монодромии N = АТМА. В новой системе координат ортами являются векторы а^, г = 1,4, совпадающие с соответствующими столбцами матрицы А. Орт а4 дает касательную к решению х0(1), а орт а3 ортогонален линиям уровня функции Гамильтона. Поэтому матрица N имеет вид:
А П12 «13«
= 0 П22 «23«24
0 010'
\ 0 «42 «43«44/
Характеристический многочлен Р(р) матрицы N имеет вид Р(р) = (р — 1)2х х(р2 — 2sp + 1), где s = (п22 + п44)/2. Число s определяет устойчивость решения в линейном приближении. Если |s[ < 1, то решение орбитально устойчиво в первом приближении, а при |s| > 1 движение неустойчиво. Рассмотрим случай |s| ф 1.
Из симплектичности матрицы N следуют равенства:
«22 «44 ~ «24«42 = 1,
«42«23 ~" «22«43 = «12,
«44«23 ~ «24«43 ~ «14,
«22«14 — «24«12 = «23,
«42«14 — «44«12 = «43, причем независимыми являются только три равенства из пяти. В этой системе координат уравнения относительно z,dT принимают вид
N4z + vdTa4 = 0, (15)
где и — модуль начальной скорости, и = |JVK(xo(O))|, а матрица Nx имеет вид
|
/0 |
”12 |
”13 |
”14 ^ |
|
|
Nx = N - Е = |
0 0 |
”22 ~ 1 0 |
”23 0 |
”24 0 |
|
^0 |
”42 |
”43 |
”44 - |
Система всегда имеет частное решение, соответствующее сдвигу по исходному периодическому решению x0(t) на произвольную величину сь
= щ, z2 = 0, г3 = 0, 2:4 = 0, dT = 0.
Общее решение системы представимо в виде z = cxai + z', dT = -(n12^ + zzi3^3 + n^z^pu, где вектор z' ортогонален вектору ax.
Поскольку мы исследуем только продолжение семейства периодических решений, то достаточно ограничиться случаем, когда rangNi = 3, то есть минор т5 матрицы Ni отличен от нуля, и, следовательно, среди миноров т2, т3, т4 есть ненулевые. Здесь
”12 = ”23 — ”14, т3 = 2 — п22 — п44, т4 = п43 + п12, Т”5 = "(”12”12 + ”13”13 + ”14?”4).
В этом случае общее решение системы (15) принимает вид
^=1?!, z2 = т2с2. z3 = m3c2, z4 = т4с2, dT = m^c2/v, где ci и с2 — произвольные постоянные. А вектор b = т2а2 + т3а3 + ш4а4 (17)
дает в фазовом пространстве направление касательной к единственному семейству периодических решений, проходящих через решение Xo(i) и имеющих период, близкий к Т.
Для симметричных периодических решений формула (17) упрощается. В зависимости от типа симметрии матрица монодромии М вычисляется по одной из формул (8), (11), (13). Непосредственной проверкой можно убедиться, что ее элементы связаны соотношениями:
m33 = тП, т44 = 77122, т43 = — 77112, т23 = —Ш|4, 77134 — —77121, ^41 — — т32-
Матрица перехода к локальному базису А будет иметь вид
Эти соотношения приводят к упрощению матрицы N
Л П12 П13 п14\ м О П22 —»14 ^24 0 0 1 о
\0 П42 -П12 7122/ и миноров матрицы Nj:
т2 = -2tzi4, т3 = 2(1 - п22), т4 = 0, т5 = -(п12т2 + п13т3).
Тогда вектор b запишется в виде векторов Ь] или Ь2, где bi = m2
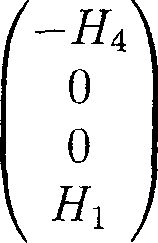
+ тп3
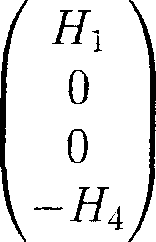
b2 = т2
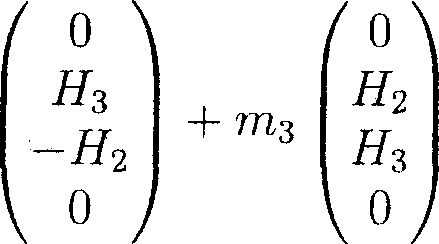
Данная формула показывает, что вектор bi имеет нулевые проекции на оси ж2 и д3, а вектор Ь2 на оси Х\ и ж4, соответственно, а значит, если хотя бы один из миноров т-2, m-j отличен от нуля, то продолжение симметричного относительно оси х4 или х2 решения дает симметричное периодическое решение.
Для симметричных периодических решений стандартное условие периодичности вида х(0) = х(Т) может быть заменено в зависимости от типа симметрии одним из следующих условий:
-
1. В случае орбит, симметричных относительно оси хг с начальным условием т2(0) = д3(0) = 0, имеем х^Т)^ = д3(Т/2) = 0.
-
2. В случае орбит, симметричных относительно оси х2 с начальным условием zi(0) = ж4(0) = 0, имеем х^Т/^ = д4(Т/2) = 0.
-
3. В случае орбит, симметричных относительно осей х4 и х2 с начальным условием д2(0) = ж3(0) = 0, имеем жДТ/4) = х4(Т/4) = 0.
-
4. В случае орбит, симметричных относительно осей х4 и х2 с начальным условием Д1(0) = х4(0) = 0, имеем х2(Т/4) = д3(Т/4) = 0.
Эти условия означают, что периодическая орбита ортогонально пересекает соответствующую координатную ось. Таким образом, симметричное периодическое решение однозначно определяется трехмерным вектором X = (жДО), ж4(0),Т) в случаях 1 и 3 или X = (т2(0), ж3(0), Т) в случаях 2 и 4.
Введем в рассмотрение векторную функцию F(X) е R2. Первые два компонента вектора F берутся из соответствующих условий периодичности. Тогда задача поиска и продолжения симметричного периодического решения сводится к задаче поиска и продолжения стационарных точек Х^ уравнения F (Х^ = 0, для каждой из которых нам известен вектор Х^\ задающий направление продолжения семейства в этой точке. Вектор Х^ состоит из соответствующих компонентов вектора b и dT = m^/v.
Наиболее простым и эффективным методом продолжения, по-видимому, является метод продолжения по длине дуги, позволяющий проходить точки поворота на ветви X(s). Пусть известно некоторое периодическое решение Х^0- = (хг(0), ^(0), Г) и нормированный вектор Х^ — касательный к ветви продолжения семейства. Тогда следующее периодическое решение этого семейства Х^) может быть найдено из решения системы
( FT (Х^) = 0, j F2 (Х^) = О, (21)
[ (х(|) - Х<“>,Х(“>) = As.
Здесь As — шаг вдоль ветви, который может выбираться априорно и может корректироваться в зависимости от скорости сходимости итераций.
Иллюстрация метода показана на рисунке 1 для случая, когда dimX = 2.
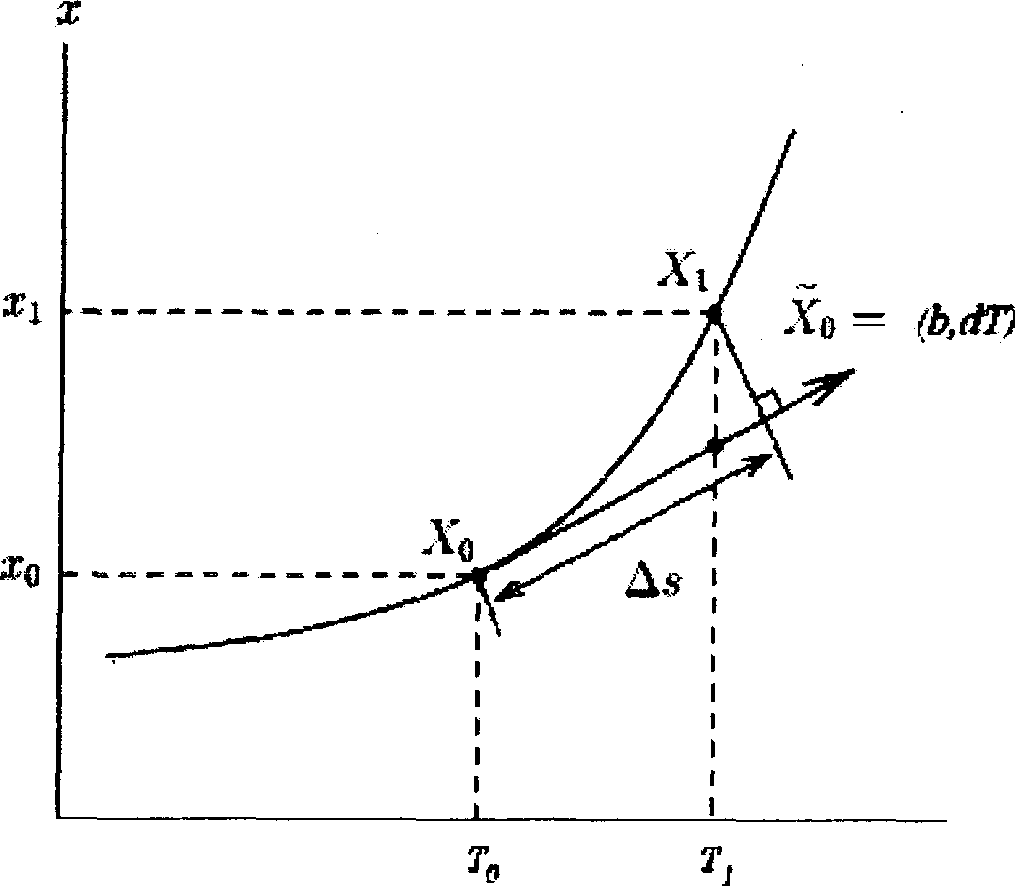
Рис. 1. Графическая интерпретация метода
Система (21) может быть решена с использованием ньютоновых итераций, а ее якобиан легко может быть построен с использованием значений матрицанта системы (2) и правых частей канонических уравнений (1), вычисленных во второй ортогональной точке, а также с помощью вектора Х-°\ Приведем вид якобиана системы (21) для случая симметрии 4. Для других случаев якобиан строится анало гично.
а Ли(т/2) Ум(т/2) ндат
(Х(1>) = Т31(Т/2) У34(Т/2)
OX I S(O) ?(») vl°>
Можно показать, что в регулярной точке семейства якобиан (22) невырожден.
2. Описание алгоритма
Пусть известно некоторое периодическое решение, обладающее, по крайней мере, одной из симметрий (4) или (11). Тогда существуют две точки, в которых орбита ортогональна координатной оси. В случае одной симметрии эти точки лежат на одной координатной оси, а в случае двух симметрий — на разных. Обозначим эти точки А и В, соответственно. Продолжение семейства возможно как из первой, так и из второй точки.
Для работы алгоритма необходимо задать ряд априорных величин:
-
• абсолютная и/или относительная погрешность интегратора системы (2);
-
• Да — начальная величина шага смещения вдоль семейства;
-
• абсолютная и/или относительная погрешность определения периодического ре
шения;
-
• Nmai — максимальное число ньютоновых итераций;
-
• условия выхода из алгоритма.
Алгоритм представляет собой предикторно-корректорную схему продолжения семейства периодического решения. Предикторная часть состоит в вычислении матрицы монодромии по одной из формул (9), (12) или (16) и в определении вектора поправок X к начальным условиям. Корректорная часть реализует решение системы (21) с помощью ньютоновых итераций. Условия выхода из алгоритма продолжения могут состоять либо в выходе начальных условий, определяющих периодическое решение, а также индекса устойчивости за априорно заданные границы, либо в получении заданного числа точек семейства. Аварийный выход из алгоритма продолжения происходит при превышении заданного числа итераций Nma$, либо при сходимости к периодическому решению с другими начальными условиями.
Более устойчивым показал себя вариант алгоритма с адаптивным выбором шага смещения AS. Априорный выбор шага обычно затруднителен, более того, его величина существенно зависит от устойчивости решения, которая может меняться в большом диапазоне вдоль семейства. Изменение As может производиться следующим образом. Определим три дополнительных параметра: ZXsmin — минимальный шаг, ZXsm(M — максимальный шаг, а — «агрессивность» смены шага. Пусть As^ — величина шага для г-й точки семейства, А^ — число итераций, выполненных для уточнения г-й точки. Возможны следующие случаи:
-
1) Ni < Nmax. шаг меняется по формуле
при Asi+i < Z\smax,
△ S
^^maxi
При Asi-ц > Z\smax.
-
2) Ni > Nmax' шаг делится пополам и повторяется попытка;
-
3) Asj < Asmin: происходит аварийное завершение алгоритма.
Если необходимо получение эквидистантных точек семейства периодических решений, то параметр а полагается равным нулю.
Во многих задачах небесной механики продолжение семейств периодических решений приводит к орбитам соударения, то есть к орбитам, проходящим сколь угодно близко к одному из тяготеющих центров. Численное исследование таких траекторий в исходных переменных становится практически невозможным. Стандартный способ заключается в регуляризации уравнений движения. Однако лишь небольшое число небесно-механических задач допускает глобальную регуляризацию, поэтому чаще всего приходится пользоваться локальной регуляризацией. Для гамильтонианов с двумя степенями свободы и с особенностями вида 1/т наиболее простой является регуляризация Леви — Чивита
(ХА _ (Qi — Q^X ((Qi ~QcA /-РД д
~ ДД Qi ) W ~ 2r Qi APsFdr + w ■
(23) Здесь r = Д(Д+Д| = Ql + QX, (Qi, Q2, Л, ^2), т — регуляризованные переменные и время.
Интегрирование уравнений движения (1) с применением локальной регуляризации приводит к некоторым техническим сложностям, но существенно повышает как точность численных результатов, так и скорость расчетов, поскольку регуляризация приводит и к стабилизации уравнений движения. Вокруг каждой из особенностей аг гамильтониана определяем окружность некоторого априорного радиуса Rsafe- Если в процессе интегрирования точка орбиты ri попадает в окрестность особенности а,;, то производится переход в локально регулярные координаты, и интегрирование продолжается в новых координатах, пока не будет покинута «опасная» область.
Метод продолжения семейства симметричных периодических решений, описанный в разделе 1, требует вычисления матрицы монодромии путем интегрирования уравнения в вариациях (2). Для орбит соударения удобно заменить уравнение в вариациях его дискретным аналогом. Для этого зададим вариацию начального условия периодического решения в виде набора одномерных сеток с к узлами вдоль каждой из координатных осей. Поскольку вариация изохронная, то каждый из 4к узлов сетки задает начальное условие задачи Коши для уравнения (1). Решая эти задачи на интервале, соответствующем типу симметрии (Т/2 для однократно симметричных, Т/4 — для двукратно симметричных орбит), и используя соответствующую разностную схему, получим значения элементов матрицанта Y(Q и, следовательно, матрицу монодромии М. Заметим, что такой способ вычисления может быть легко распараллелен на 4к независимых процессов, что существенно повышает скорость счета без изменения процедуры интегрирования системы уравнений.
Если в процессе продолжения семейства одна из точек ортогонального пересечения оси орбитой попадает в окрестность особой точки гамильтониана, то даже регуляризация не позволяет корректно определить матрицу монодромии. Была опробована адаптивная схема, позволяющая выбирать такое условие периодичности, чтобы и начальная, и конечная точки находились вне окрестности особой точки. Продемонстрируем идею на следующем примере. Пусть периодическое решение обладает симметрией (4), то есть в качестве начальной точки А может быть выбрана точка с координатами (ж^4, 0, 0, х^. Пусть для этого условия выполнено |ж^| > Rsafe- В силу условия симметрии через интервал Т/2 в точке В орбита будет иметь координаты (х®, 0,0, х^. Если [ж^| < Rsafe, то при определении элементов матрицы М возможны большие погрешности, которые не позволят корректно продолжить семейство. Заменив условие периодичности на полупериоде Т/2 условием ж® (Т) = х®(Т) = 0 на периоде, обеспечим определение элементов матрицы М, а значит и параметров продолжения семейства с необходимой точностью. При этом почти вдвое увеличиваются вычислительные затраты. Если по мере продолжения семейства точка, соответствующая половине периода, покидает окрестность особенности, то можно вернуться к более экономной схеме, основанной на условии периодичности на половине периода. Покажем некоторые результаты применения данного алгоритма.
3. Продолжение семейств задачи Хилла с различными симметриями
Рассмотрим применение описанного выше алгоритма для продолжения семейств симметричных периодических решений плоской задачи Хилла, являющейся предельным случаем ограниченной задачи трех тел. Интерес к этой задаче объясняется рядом причин. Во-первых, занимая в некотором роде «промежуточное» положение между интегрируемой кеплеровой задачей и неинтегрируемой ограниченной задачей трех тел, гамильтониан задачи Хилла обладает лишь одной особенностью, как и гамильтониан первой задачи, но при этом задача Хилла является неинтегрируемой, как вторая задача. Такой подход позволяет рассматривать задачу Хилла как возмущение кеплеровой задачи, а ограниченную задачу трех тел — как возмущение задачи Хилла. Во-вторых, гамильтониан задачи Хилла допускает два преобразования (4) и (10), а значит существуют периодические решение как с одной, так и с двумя симметриями относительно осей Ж1 и Ж2. Будем обозначать симметрию относительно жу символом Xi, а симметрию относительно ж2 — Х2.
Пусть х = (ж1,Ж2,ж3,ж4) — вектор канонически сопряженных координат и импульсов, тогда гамильтониан задачи Хилла имеет вид
-
(х) = 2 (жз + ЖТ) + ж2ж3 - жьж4 - ж^ + |ж| - |, (24)
где г = ^Ч + ж2- Задача Хилла обладает единственным первым интегралом Я(х) = — 2С, где С — постоянная Якоби, равная
о
Основными семействами периодических орбит задачи Хилла являются семейства а, с, f, д, описанные в статье [5]. Будем называть их семействами периодических решений первого рода.
Первые два семейства а и с происходят от либрационных орбит, являются взаимносимметричными относительно оси ж2 и обладают симметрией Их можно также рассматривать как продолжение ударных кеплеровых орбит. Эти семейства неустойчивы при всех значениях постоянной С Е (—оо; 34//3), а значит не могут быть порождающими решениями для семейств периодических решений второго рода.
Семейства / и д представляют собой, соответственно, обратнооборотные и прямооборотные спутниковые орбиты, которые можно рассматривать как продолжение, соответственно, обратных и прямых круговых орбит кеплеровой задачи. Орбиты этих семейств дважды симметричны. Семейство д устойчиво лишь при значениях постоянной С > 4,999, а его индекс устойчивости имеет минимум Smtn ~ 0,827 < cos(2tt/11). Следовательно, семейство д не может быть порождающим для периодических орбит с числом оборотов меньшим 11. Семейство / устойчиво при всех значениях постоянной С, а индекс устойчивости s —» 1 при С —» ±оо и имеет минимум smiU « —0,691. Значит семейство / играет роль порождающего для периодических решений второго рода. Среди периодических решений второго рода, порожденных /, особую роль согласно [6] играют орбиты, которые, пройдя соударение и став прямооборотными, разрушают инвариантные торы вокруг семейства д и формируют зоны динамического хаоса. Некоторые из этих семейств были замечены еще М. Нёпоп в [5] и описаны в работе авторов [7].
-0.5 -0.4 -03 -0.2 -ОЛ 0 0.1 0.2 ОЗ 0.4 05
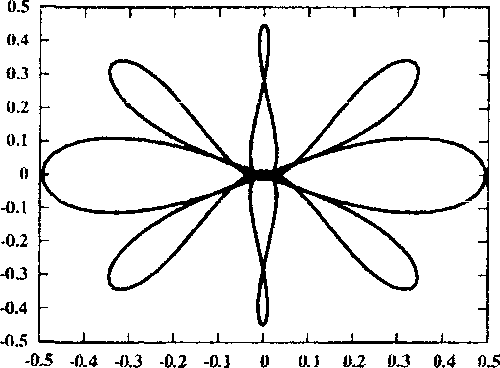
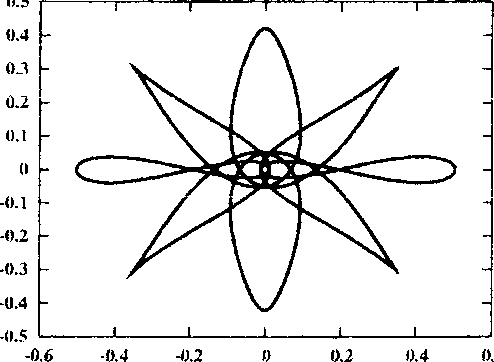
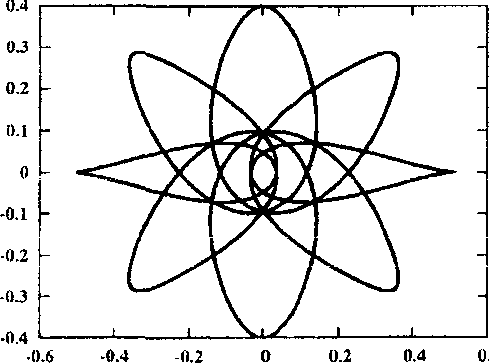
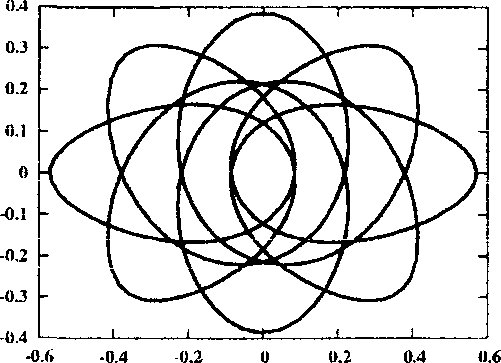
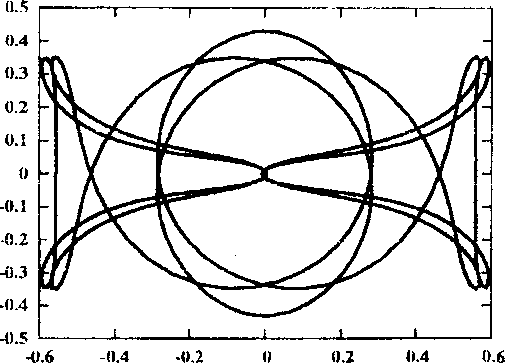
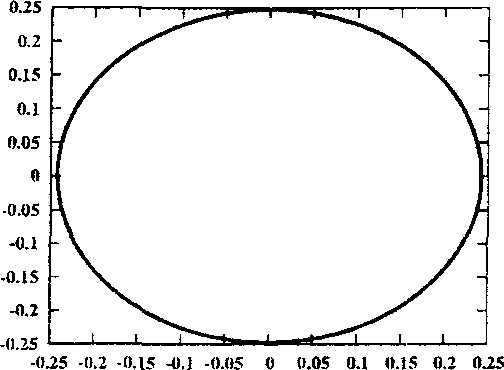
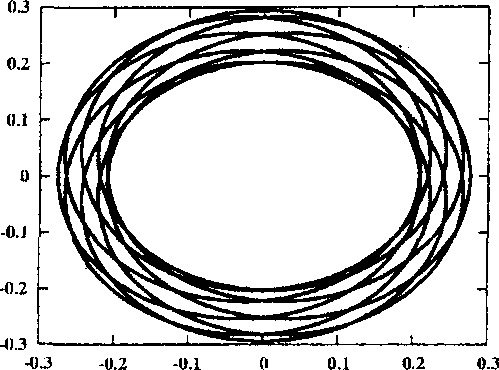
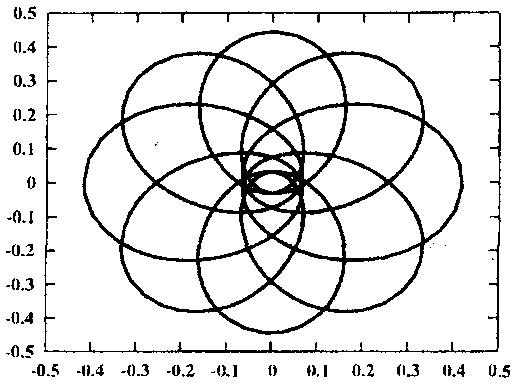
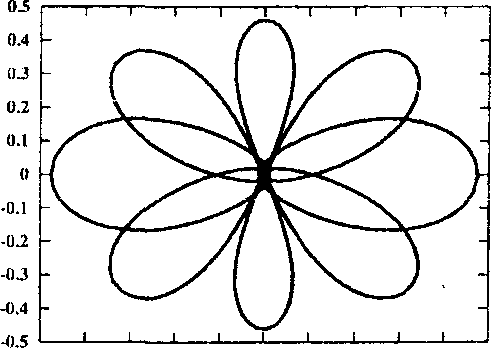
Рис. 2. Семейство дважды симметричных периодических орбит второго рода, порожденных семейством /
Рассмотрим эволюцию одного из таких семейств — семейства дважды симметричного периодического решения второго рода, которое порождается семейством / с соизмеримостью 1 : 9.
При С ~ 3,1551473 индекс устойчивости орбиты / становится равным со5(2тг/9), и от нее ответвляется пара дважды симметричных девятиоборотных периодических
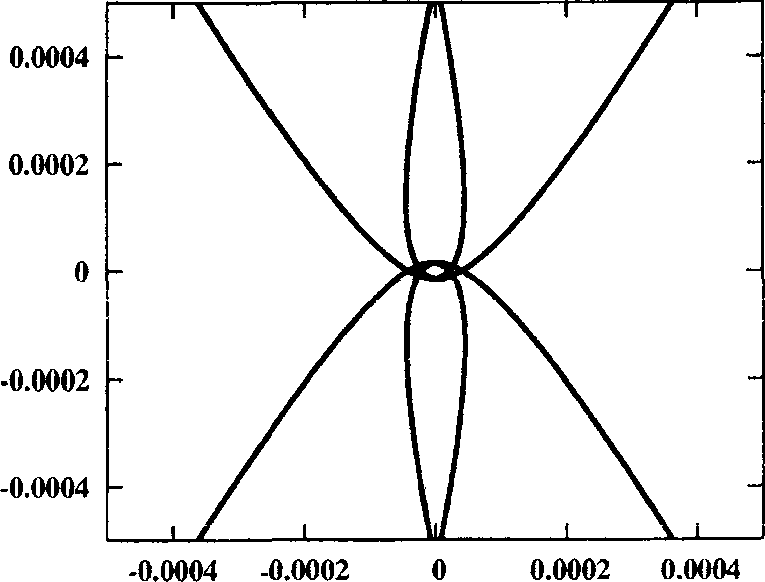
Рис. 3. Окрестность начала координат для орбит, близких к ударным решений. Орбита / в момент ответвления показана на кадре 1 рисунка 2, а неустойчивое решение при С и 3,1726323 на кадре два. При дальнейшем увеличении С орбита приближается к ударной (кадр 3), и, наконец, дважды при С ~ 4,1598531 (кадр 4) и С Ri 4,4561743 (кадр 5) проходит через особую точку — начало координат. Окрестность особой точки для этих орбит показана на соответствующих кадрах рисунка 3. После этого орбита меняет свои топологические свойства и становится прямой семиоборотной (кадр 6). Семейство достигает максимума по Ста1 ~ 4,7362746 и меняет устойчивость (кадр 7). Вплоть до С и 4,3562484 орбита устойчива, а ее индекс устойчивости последовательно убывает от 1 до — 1, а затем возрастает до 1 (кадр 8). При этом семейство испытывает бифуркацию потери симметрии, то есть от него ответвляется пара однократно симметричных семиоборотных орбит. Дальнейшее продолжение семейства приводит к сильно неустойчивым решениям, которые стремятся к ударным либрационным орбитам. На кадре 9 рисунка 2 показана такая орбита при С ~ 3,9602859 с индексом устойчивости s ~ 1,082 • 1010.
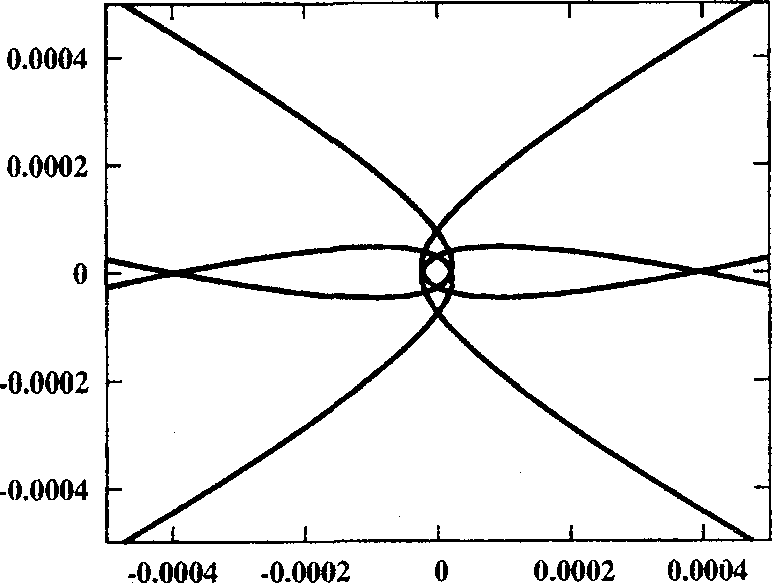

Рис. 4. Семейство симметричных относительно OY семиоборотных орбит
Поскольку индекс устойчивости двояко симметричного семейства проходит через 1, то от него ответвляется пара несимметричных орбит. В данном случае это орбиты с единственной симметрией S2. Эволюция этого семейства приведена на рисунке 4, При С ~ 4,33892 данное семейство испытывает бифуркацию потери симметрии и порождает пару несимметричных решений. Само семейство становится сильно неустойчивым и вновь проходит через начало координат.
Были исследованы и другие семейства периодических решений с симметрией Si. Во всех случаях метод давал результаты хорошего качества при небольших вычислительных затратах.
Список литературы Продолжение семейств симметричных периодических решений гамильтоновых систем через точки соударения
- Крейсман Б.Б. О симметричных периодических решениях плоской ограниченной задачи трех тел: Препринт ФИАН им. П.Н. Лебедева. № 66. М., 1997.
- Крейсман Б.Б. Семейства периодических решений гамильтоновой системы с двумя степенями свободы. Несимметричные периодические решения плоской ограниченной задачи трех тел: Препринт ФИАН им. П.Н. Лебедева. № 30. М., 2003.
- Batkhina N.V., Batkhin A.B. High precision algorithms of numerical integration of celestial mechanics problems//IAA Transactions. "Celestial Mechanics", 2002. № 8. P. 22-23.
- Якубович В.А., Старжинский В.М. Параметрический резонанс в линейных системах. М.: Наука, 1987.
- Hénon M. Numerical Stability of the Restricted Problem: Hill's Case: Periodic Orbits and their Stability//Astron. & Astrophys. 1969. № 1. p. 223-238.
- Симо К., Стучи Т. Центральные устойчивые/неустойчивые многообразия и разрушение КАМ-торов в плоской задаче Хилла. Ижевск: Ин-т компьютерных исследований, 2002. С. 90-141.
- Сумароков С.И., Батхина Н.В., Батхин А.Б. Бифуркации периодических решений в модели Хилла//Вестник ВолГУ. Сер. 1: Математика. Физика. Вып. 2. 1997. С. 49-57.


