Проекционный принцип построения функционально-воксельных моделей

Задача автоматизации построения пространственной модели по её чертежам является актуальной, поскольку с приходом автоматизированных подходов к проектированию возникла задача заполнения баз данных конструкций [1-7]. Задача состоит в описании модели объекта в 3D-пространстве, что влечёт за собой описание проекционных связей между проекциями и обеспечение перехода к другому измерению каждого из пространственных элементов, составляющих геометрический объект. Подходы к такому переходу средствами параметриза- ции, предложенные в [1], а также в других отечественных [2-5] и зарубежных работах [6-8], позволяют подойти к решению задачи, но пока не привели к полноценному алгоритму построения цифровой 3D-модели, обеспечивающей требуемую точность описания поверхностей объектов параметрическими функциями. Интересные результаты достигнуты в [9] посредством применения искусственного интеллекта при распознавании чертежа. В этой работе, несмотря на воксельное представление результата, «теряются» основные геометрические характеристики восстанавливаемого объекта. Задачу увеличения размерности геометрического объекта целесообразно привести к обобщённому виду для многомерного пространства.

• 1    Постановка задачи

Один из прогрессивных подходов к многомерному геометрическому моделированию на базе функций В.Л. Рвачёва [10] ( R -функциональное моделирование, RFM ) описан в [11, 12]. Суть подхода – в моделировании плоского контура чертежа аналитическими функциями, описывающими области значений, характеризующих нулевую границу плоского геометрического объекта, положительную зону значений внутри и отрицательную снаружи. В аналитическом представлении геометрический объект легко поддаётся увеличению размерности его пространства. В качестве примера предлагается рассмотреть принцип построения четырёхмерного пространства аргумента для заданной функции у = f ^{[ 1} ] (х) одномерного пространства (в квадратных скобках указывается размерность пространства аргумента функции). На рисунке 1 изображен график функции для одномерного пространства аргумента.

Перенос значения переменной в правую часть уравнения переводит её в аргумент, а уравнение при этом приобретает неявный вид:

• ^{[2 ]} (х,у) = f^{[ 1]} (х) - У = 0.

Все точки на кривой приобретают нулевое значение, а закон рассматриваемой кривой определяется поверхностью для двухмерного пространства аргумента как показано на рисунке 2 и записывается как: z = f ^{[2 ]} (х,у).

Повторение этой процедуры к вновь полученному уравнению преобразует функцию к неявному виду:

f ^[3 ] (х, у, z) = f ^{[2 ]} (х,у) — z = 0 или и = f ^{[ 3} ] (х, у, z).

Значения теперь обнуляются на поверхности и образуют трёхмерные области положительных и отрицательных значений (рисунок 3).

Процесс можно продолжать далее, наращивая размерность пространства аргумента, однако зрительно сложно себе представить получаемые геометрические объекты.

Аналитический подход к описанию геометрических моделей сопровождается сложными вычислениями и долгое время считался непригодным для автоматизации. Попытки применения RFM к построению поверхностных моделей [13] привели к значительной потере полезных данных, содержащихся на области описываемого функционала и, главное, к потере основного свойства увеличения размерности. В [14, 15] предложен метод функционально-воксельного моделирования (ФВ-моделирование), позволивший построить компьютерную модель таким образом, что она в целом сохраняет свойства аналитической модели на выбранной области в многомерном пространстве. Исследования показали, что такой подход к моделированию может позволить решать различные задачи геометрического моделирования на компьютере [16-19], а также вполне применим к задаче построения пространственного геометрического объекта по его аналитическим проекциям (чертежам). В предлагаемом материале ставится задача сформулировать аналитические принципы основных процедур получения описания 3D геометрического объекта по его плоским проекциям, описанным аналитическими функциями, представленными на компьютере в виде ФВ-моделей.

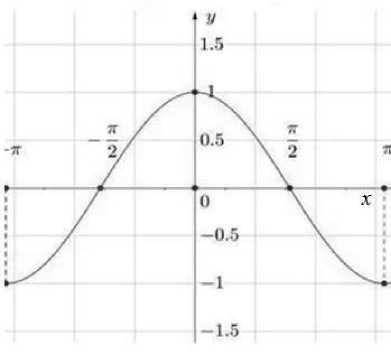
Рисунок 1 - График функции у = с о s х

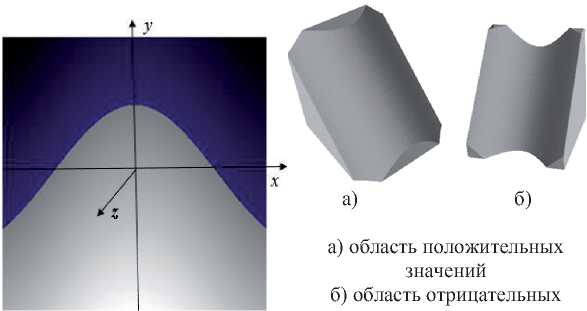
значений

Рисунок 3 – Значения области функции и = с охх — у — Z

Рисунок 2 – График функции Z = с о хх — у

• 2  Функционально-воксельное моделирование

Метод ФВ-моделирования хорошо зарекомендовал себя в ряде прикладных направлений, среди которых: компьютерное моделирование R -функциями объектов аналитической геометрии, решение задач многомерного моделирования, расчёт физических характеристик в инженерных задачах, прокладка градиентного спуска с учётом препятствий к намеченной цели в задачах оптимизации. При этом аналитическая функция F(X_m) = 0, описывающая геометрический объект, представляется набором графических М -образов (М ^ ...,М_{т +г}), содержащих данные для формирования области локальных функций L (т_т, т _{т +г} ) = 0. Здесь – компоненты нормированного однородного вектора градиента в рассматриваемой точке. Каждая локальная функция моделирует линейную аналитическую зависимость ^п 1 X i + — + п_т х_т +п_{т +1} = 0, поведение которой в рассматриваемой точке полностью соответствует исходной аналитической функции F( X m= = 0, что позволяет использовать её в дальнейших расчётах. Такой подход к представлению геометрической информации позволяет решать задачи компьютерного моделирования на уровне применения локальных функций в каждой точке рассматриваемой области. Подобное представление функции позволяет применять к ФВ-моделям функциональные операции, что значительно расширяет возможности моделирования многомерных геометрических объектов сложной формы, выполняя такие упрощённые вычисления.

Размерность пространства для функции определяет количество её аргументов, поэтому количество слагаемых локальной функции определяется количеством аргументов, увеличенным на два слагаемых. Например, функция z = f(x, у) имеет два аргумента x, у , а значит четыре слагаемых определяют локальную функцию; п₁ х + п₂ у + п ₃ z + п₄ = 0. На рисунке 4 показана схема получения компьютерного представления заданной области такой функции в виде М -образов.

Предложенным способом можно кодировать информацию об аналитической функции любой размерности, описывая геометрические объекты любой сложности на заданной области аргументов. На рисунке 5 показано описание сложной геометрии, представленной тремя аргументами пространства (х, у, z) в виде пяти многослойных М-образов, где каждый слой образов в заданной точке области характеризует значение . Кодировка цвета в точке каждого из М-образов представляется в     (Red, Green, Blue – цветовая модель) формате единым целочисленным значением, представляющим соответственно 167772161 возможных положительных целых чисел (Мi = 0 ... 16777215), а значит точность представления значений компоненты щ доведена до пятого знака после запятой. Трёхмерный объект представлен пятью такими компонентами локальной функции (рисунок 5).

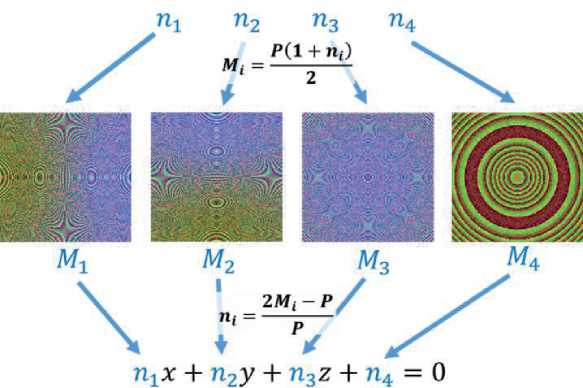
Рисунок 4 – Графическая кодировка области функции набором М -образов с последующим получением локальной функции L(x, у, z, N₄) = 0

Рисунок 5 – Графическая кодировка области функции набором М -образов с последующим получением локальной функции LXx, у, z, и, N) ) = 0

• 3    Принцип проекционного ФВ-моделирования

Можно отметить сходство между традиционным конструированием на проекциях и аналитическим конструированием на функциях, а также единство в проекционном применении аналитического описания геометрических объектов. Например, аналитическое описание цилиндра радиусом основания и высотой можно представить двумя функциями с пространством аргумента более низкой размерности, т.е. функциями двухмерного пространства аргумента и одномерного: f(x,y) = г- — х- — у² и g(z) = h- — z ² . На рисунке 6 представлены ФВ-модели соответствующих функций, где М -образы распределены в соответствии пяти положениям в трёхмерном пространстве аргумента. Чтобы обеспечить этим ФВ-моделям про-

1 Каждый цвет в RGB имеет 256 оттенков от 0 до 255, то есть всего 256 * 256 * 256 = 16 777 216 возможных оттенков.

ективное свойство в трёхмерном пространстве аргумента функции «цилиндр», достаточно дополнить недостающие М -образы «нулевыми», т.е. отображающими нулевое значение в каждой точке, образами. Результат представлен на рисунке 7.

f(x,y.u)

Рисунок 6 – Последовательное расположение М -образов согласно пяти компонентам локальной функции четырёх аргументов (х, у, z , и)

Рисунок 7 – Заполненная последовательность расположения М -образов согласно пяти компонентам локальной функции четырёх аргументов (х, у, z, и)

В аналитическом способе пересечение и объединение положительных и отрицательных значений на заданной области двух функций осуществляется

посредством R -функционального моделирования. Например, функция пересечения двух функций выглядит следующим образом: R (х, y,z= = f(x,y) + д (z) — ^f (х,у) 2 + д (z)2 или и = и ++ и - — U и 2 + и 2 ,       где        и = = г 2 — х2 — у 2 , и 2 = h 2 — z2. Можно также использовать локальные функции в точках ФВ-модели: „ [1]                                          „[ 2 ]       „[ 2 ] и1 = — щх — [Лу — щ,и2 = — [2]z — й '^4         '^4          '^4               '^4        '^4 Полученные точки положительного значения области показаны на рисунке 8.

Рисунок 8 – Фигура, построенная R -функцией пересечения согласно положительным значениям и = и + и 2 — ^и 2 + и | .

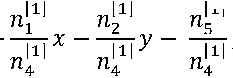
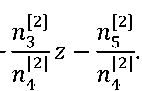
• 4    Функционально-воксельное пересечение

В задаче, представленной в разделе 3, осуществлялось выделение точек трёхмерного пространства для положительной области пересечения двух функций f (х, у) и g(z). Для перехода к задаче получения ФВ-модели той же трёхмерной фигуры «цилиндр» необходимо выразить функцию, которая по примеру функции В.Л. Рвачёва выполняет послойное формирование М -образов, представляющих область функции «цилиндр» на основе полученных

ФВ-моделей для f (х,у, z,u) и д(х,у, z.u). Значение цветовой градации Mj в точке М-образа пересчитывается в компоненту вектора пi = (2Мi — Р// Р, где i = 1^5, P - 16777216 градаций цвета. В результате записываются локальные функции для обеих ФВ-моделей: n[1 ]х + п[1 ]у + n^z + п^и + n[1] = 0 и n[2 ]х + n[2 ]у + n[2 ]z + n[2 ]и + n[2 ] = 0. Деление всех компонент на компоненту при аргументе и (это компоненты n[1 ] и n[2 ]) приводит к записи:

• [1][2 ]

, [ 1 ]      _ n1,2,3,5 ,[2 ]      _ n1,2,3,5 ,[ 1 ][2 ]

• 1    1,2,3,5           [1 ] ,Z 1,2,3,5           [2 ] , Z4        Z4

П4

Рассчитываются значения для обеих функций на основе полученных коэффициентов

(компонент) I:; u ^[1] = — Z ^[1] x — Z2^{1 ]} y — I 3^{1 ]} z — I 5^{1 ]} , u ^{[2 ]} = — Z ^[2] x — Z ^[2] y — Z ^[2] z — Z ^[2] .

Окончательное выражение закона для определения компонент локальной функции со- гласно R-функции пересечения записывается как:

= 1, Z = 1,2,3,5.

[ 1 L.[ 1 ]      [2 ]„[2 ]  \

Z ^[R] = Z ^{[[ 1 ]} + Z ^{[[2 ]} — (                '           ),  Z f ^]

7(u ^{[ 1]} ) ² + (u ^{[2 ]} )² /     ⁴

Результат получения ФВ-модели цилиндра показан на рисунке 9.

Рисунок 9 – Скомпонованная композиция из пяти трёхмерных М-образов и фигуры цилиндра, полученной на их основе

Количество и сложность проекций можно увеличивать, а также применять процедуру объединения:

+.-+(дай;) c

7(u ^{[ 1 ]} ) ² + (u ^{[ 2 ]} )

= 1, Z = 1,2,3,5.

На рисунке 10 показано пересечение трёх проекций, обеспечивающих полому цилиндру

два дополнительных сквозных отверстия с круглым и квадратным сечениями. Для наглядности проекции представлены ортогонально друг другу с выделением положительной области значений. В центре рисунка 10 помещена объёмная фигура, полученная в результате трёх последовательных пересечений.

5 Закон функционально-воксельного вращения

Закон ФВ вращения можно показать на примере построения сферы по одной проекции – окружности. Если применить шесть проекций (сверху, снизу, справа, слева, спереди и сзади) в виде окружностей, то при их пересечении сфера не получится. Отсюда следует, что для описания сферы по проекциям необходимо дополнительно указывать, что трёхмерная фигура является сферой, как фигура вращения её проекции (окружности).

Локальную функцию единичной сферы можно записать, применив её проекционную локальную функцию окружности с единичным радиусом, заданную на области от -1 до 1 по двум осям в плоскости xOz : и = 1 — х ² — z ² .

Рисунок 10 – Композиция из трёх проекций М -образов и фигуры, полученной на их основе

Для получения единичной сферы достаточно вместо координаты x вписать закон вращения в плоскости    :

х ‘ = ^х ² + у ² .

Аргументы под корнем определяют плоскость вращения (х О у) . Подстановкой вместо аргумента x закона вращения ( ′ ) получается уравнение единичной сферы:

и = 1 — (^х ² + у ² ) — z ² = 1 — х ² — у ²

-

z ² .

Локальная функция, описывающая точки на заданной области сечения сферы в плоскости хО z, содержит следующее выражение: п_х х + п₃ z + п₄и + п 5 = 0.

Замена аргумента x выражени ем зако на вращения ( ′ ) в локальной функции даёт:

П ^х ² + у ² + п ₃z + п₄ и + п ₅ = 0.

Умножением на выражение закона вращения всех компонент функции получается:

п_х (^х ² + у ² ) + п ₃ z ^х ² + у ² + п ₄и ^х ² + у ² + п ₅ ^х ² + у ² = 0.

В результате преобразований формируется локальная функция, учитывающая закон вращения проекции в плоскости х Оz: (\пх | ^=^) х + (|nj ^===)у + п ₃ z + п₄и + п₅ = 0, а значит п'х = \п хЫ=, п' 2 = \пх\^==.

√             √

На рисунке 11 показана ФВ-модель сферы, полученная пересчётом компонент.

Пример вращения более сложной геометрической фигуры, составленной объединением окружности и треугольника, показан на рисунке 12.

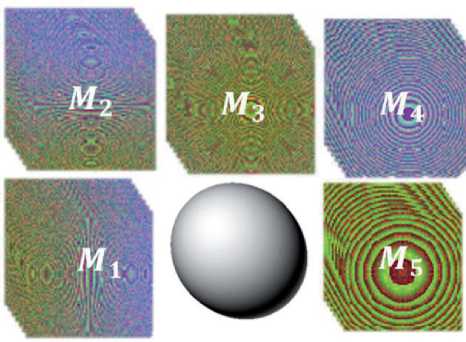
Рисунок 11 – Композиция из пяти трёхмерных М -образов и фигуры сферы, полученной на их основе

Рисунок 12 – Композиция из проекции М -образа и фигуры, полученной на его основе

Пример получения фигуры вращения для чертежа, рассматриваемого в работе [3], как способ получения функционально-воксельной 3D-модели по плоской проекции, описанной сложным контуром, представлен на рисунке 13.

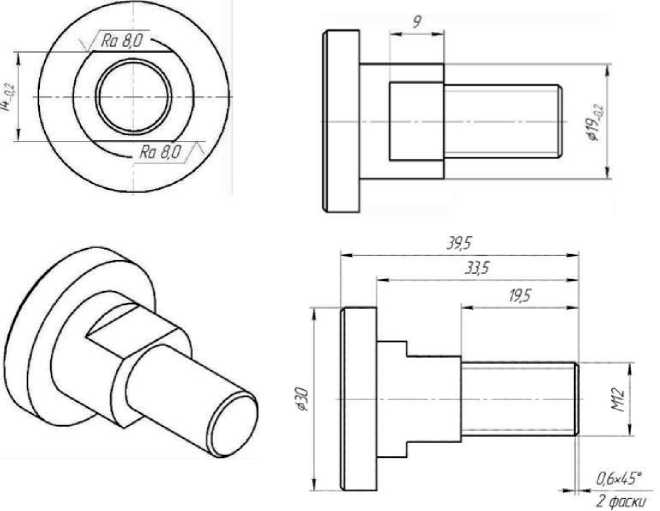
Рисунок 13 – Чертёж детали, рассмотренный в работе [3]

В [10] предложен аналитический способ описания сложного контура посредством пере-сечения/объединения полуплоскостей, задаваемых уравнением:

(Уi - y i +1 )x - U i - Xi ₊Jy + (X i+i у i - x_tyi +1 ) > 0, где i - номер текущей точки контура.

При рассмотрении обобщённой функции в контексте R- функционального моделирования получается, что:

⁽ У i - yi +1 )x - ⁽xi - Xi +Jy + (Xi +1 у - Xyyi +i ) = z_iti +i , ^w = ^z1,2 ^ ^z2,3 ^ ^z3,4 ^ ^(z4,5 ^{U (z}5,6 ^ ^z6, 7 ) ^ Z 7, ₈ ) П Z ₈ ,g П Z ₉ ,1 ₀ П Z i ₀ , 11 П

^ ^(z 1 1,12 ^{U (z} 1 2,13 ^ ^z 1 3,14 ) ^{U z} 14,15 ) ^ ^z 1 5,16 ^ ^z 16,1 -

Из этого выражения видно, что контур содержит последовательно расположенные 16 узловых точек, как показано на рисунке 14, где синим цветом выделена область отрицательных значений z. На рисунке 15 представлены четыре М - образа, кодирующие значение локальных геометрических характеристик для получения локальной функции в выбранной точке:

nx + п ₃ y + n₄z + П₅ = 0

На рисунке 16 показан результат моделирования тела вращения по полученным четырём М -обра зам п ри малом разрешении 256х256 пикселей c применением закона вращения X ' = Vx ² + z ² . В результате функционально-воксельного моделирования получается набор из пяти М -образов, описывающих трёхмерную область аргументов для локальной функции:

′ и =--x--y--z--,

П4 П4 П4 П4

где n\ = |П 1 1   "   , п‘ 2 = 1^ 1 1 -/==, nt = (2М_t - Р)/Р, i = 1 . 5.

√             √

Для получения окончательного результата моделирования, сопоставимого с аксонометрией детали рисунка 13, на рисунке 17 показано применение области отсечения.

Рисунок 14 – Поверхность положительных значений с нумерацией узлов нулевой границы

Рисунок 15 – Композиция из проекции М-образа и фигуры, полученной на его основе

Рисунок 16 – Композиция из про екции М -образа и фигуры, полученной на его основе

Заключение

Аналитическое конструирование можно рассматривать как структуру проекционных процедур. Она позволяет из проекций, как функций двух аргументов, собирать аналитическое описание сложного трёхмерного объекта. Разработанные инструменты в виде аналитических процедур пересечения, объединения и вращения, а также принципы увеличения размерности ФВ-модели позволяют моделировать 3D-область для функции описания пространственного геометрического объекта, формируя проекционные связи в виде функциональных закономерностей. Полученные результаты могут способствовать решению задачи построения функции описания трёхмерных геометрических объектов по функциям, описывающим

Рисунок 17 – Композиция из проекции М -образа отсечения и окончательной фигуры, полученной на его основе

элементы плоского чертежа.