Проектирование баз знаний робастных нечетких регуляторов в непредвиденных ситуациях управления: продукционные правила вывода с учетом информационной оценки приращения риска

Одним из критичных факторов, влияющих на качество систем управления, функционирующих в условиях неопределенности, является информационный риск, наличие которого в контуре управления существенно снижает информационную и структурную безопасность жизненно важных объектов управления (ОУ). Материальный и моральный урон, наносимый от данного фактора, хорошо известен. Источниками информационного риска в системах принятия решений и управления являются следующие: 1) проявление негативного человеческого фактора в контуре управления; 2) отсутствие необходимой информации о нештатной ситуации; 3) структурные нарушения в объекте и системе управления; 4) задержки сигналов ошибки в контурах и обратных связях управления; 5) шумы в датчиках съема и измерения данных; 6) неполное описание среды функционирования и динамики объекта управления и мн. др.

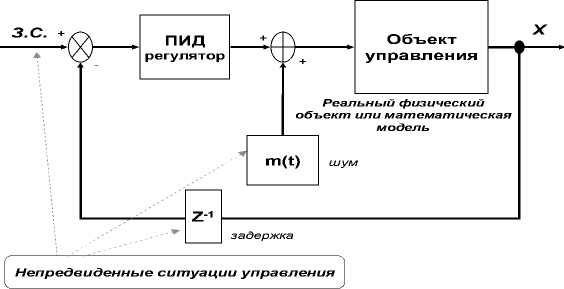
Рисунок 1 иллюстрирует типовые источники непредвиденных ситуаций управления для традиционных структур систем автоматического управления (САУ).

(а)

Объект управления:

Тип неустойчивого поведения

• -    Локальная неустойчивость

• -    Глобальная неустойчивость

• -    Неустойчивость по части обобщенных координат и нелинейные связи

Случайная структура или параметрические возмущения

Тип описания модели

• -    Математическая модель

• -    Физическая модель

• -    Слабо структурированная математическая и нечеткая физическая модель

  Внешние случайные возмущения:

  • Различные функции распределения вероятностей

  • Функции распределения вероятностей зависящие от времени

  

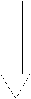
  Различные типы задающего сигнала

  
  
  
  
  
  
  
  

Система измерения:

• •    Шум в датчиках

  Различные типы структур ₅ традиционных регуляторов

  
  

• •    Временная задержка съема сигнала

• •    Случайная задержка шума в датчиках

(б)

Рис. 1. Структура САУ (а) и типовые источники непредвиденных ситуаций управления (б)

Во многих ситуациях существующий и наблюдаемый разброс в источниках непредвиденных ситуаций на рис. 1,б в действительности не хаотичен, а характеризуется определенным статистическим или вероятностным распределением p ( x ) , где x является вектором случайных событий, характеризующий непредвиденную ситуацию управления.

При обнаружении сигналов, описывающих поведение ОУ на рис. 1а, важен не только факт их наличия, но и величина необходимых информативных параметров, несущих данные об опасности возникновения нештатной ситуации, которая содержится в таких сигналах.

Целью данной работы является описание существующих объективных информационных и логических ограничений на описание непредвиденных ситуаций управления, которые необходимо учитывать при их возможном возникновении в виде оценок приращения информационного риска для разработки корректных математических моделей продукционных правил баз знаний (БЗ) нечеткого логического вывода в нечетких регуляторах (НР).

Рассматриваются возможные подходы к построению аппроксимаций и оценок робастности таких моделей, роли видов интеллектуальных вычислений (ИВ) в компенсации неточностей описания моделей непредвиденных ситуаций управления и смежных вопросов, таких как синергизм информации при разработке процессов самоорганизации информационных процессов в ИСУ и др.

Предварительно кратко рассмотрим некоторые методы теории и систем управления оценки и учета неопределенностей в структурах робастных САУ.

1.    Учет факторов неопределенности в структурах робастных САУ

Современные технологии робастного многопараметрического управления типа H 2 / H _х или смешанного µ -синтеза традиционных регуляторов и др. позволяют учитывать наличие степени неопределенности в параметрах и/или в динамическом поведении ОУ [1-16]. В данных технологиях (по аналогии с традиционным подходом в теории автоматического управления – ТАР) проектирование робастных регуляторов основано на предположении, что динамическое поведение нелинейного ОУ можно аппроксимировать с достаточной точностью линеаризованной динамической моделью. В этом случае в постановке задачи проектирования регуляторов изменения (возмущения) параметров во времени и качественное описание нелинейных характеристик ОУ учитываются в структуре системы управления и рассматриваются как «уровни неопределенности» Д .

Так, например, дробно-линейное преобразование с так называемой M -Д конфигурацией применяется в анализе задач с неопределенностями, когда система приводится к виду, изображенному на рис. 2.

Рис. 2. Структуры с M - Д конфигурацией

На рис. 2 ω – внешние возмущения, z

- выход, M = M ( s ) =

^M 11

^M 21

^M 12

^M 22

– передаточная

функция, и Д ( s ) - матричная функция, описывающая разного рода неопределенности.

В этом случае можно записать соотношения между сигналами на схеме рис. 2 в следующем виде: e = ( I - M 11 Д ) M 12 ® , z = ( M 12 Д [ I - M 11 Д ] ^{- 1} M ₂₂ ) ^ .

Таким образом, параметр неопределенности Д ( 5 ) вводится в структуру САУ и дает возможность провести анализ и синтез выбора оптимальной (адаптивной) структуры САУ.

На рис. 3 приведены структуры САУ с неопределенными параметрами [17].

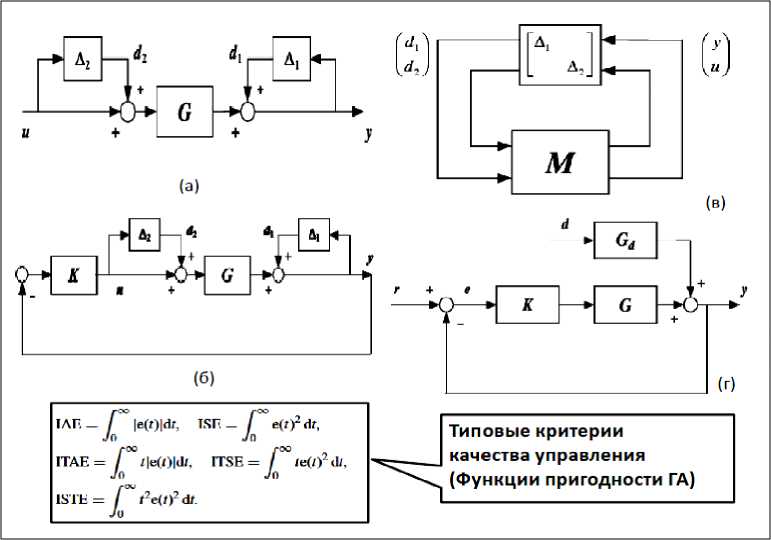
Рис. 3. Модели САУ с неопределенными параметрами структуры:

а – модель с неопределенной структурой; б – модель с обратной неопределенной связью; в - структура с M - Д конфигурацией; г - типовая структура с обратной связью

Для ОУ с передаточной функцией G на рис. 3,а имеем передаточную функцию с неопределенностью вида G _Д = ( I - Д 1 ) 1 G ( I + Д ₂ ) , Д 1 , Д 2 е H _№ .

Для анализа робастности структура с M - Д конфигурацией на рис. 3,в матрица М для передачи сигналов d1, d2 к сигналам y, и задается как M =

робастности задается параметром как y =

G

I

Для простой одноконтурной САУ имеем γ

(I + GK)- K (I + GK )-1

0 I

MT

Io I

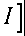
I o

(I + GK)

№

№

и критерий

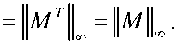
При этом сама величина параметра Д определяется экспертом. В результате существенные изменения во времени параметры и/или нелинейные неизвестные характеристики описываются в линеаризованной модели ОУ с избыточной мерой неопределенности.

В таблице 1 приведены известные в литературе [1-12, 14-17] достоинства и недостатки применяемых в робастном анализе методов.

Таблица 1. Анализ методов робастного анализа

Название	Преимущества	Недостатки
H ∞ -синтез	Работает как с устойчивостью, так и с чувствительностью системы, замкнутый контур устойчив, прямой однопроходный алгоритм синтеза	Требует особого внимания к параметрической робастности объекта управления
H 2 -синтез	Работает как с устойчивостью, так и с чувствительностью системы, замкнутый контур устойчив, точное формирование передаточной функции контроллера	Большое количество итераций
LQG-синтез	Использование доступной информации о помехах	Не гарантируются запасы устойчивости, требуется точная модель объекта, большое количество итераций
LQR-синтез	Гарантированное обеспечение робастной устойчивости, безынерционный регулятор.	Требуется обратная связь по всему вектору состояния, требуется точная модель объекта, большое количество итераций
μ-синтез	Работает с широким классом неопределённостей	Большой порядок контроллера

Отметим, что для достаточно большой меры неопределенности может не существовать регулятора, который справляется с задачей управления в такой ситуации, в частности для всех мер и форм неопределенности. Более того, спроектированный регулятор, если он существует, может своего рода быть «консервативным» в смысле отсутствия в его структуре возможности учета наихудших случаев непредвиденных (нештатных) ситуаций управления.

Существует ряд стратегий в технологии нелинейного управления как линеаризация с обратной связью, преобразования обратной динамики, скользящий режим, нелинейное демпфирование, адаптация (например, оценка параметров в on-line) и мн. др.

Однако не существует общей методологии нелинейного управления, в которой достоверно получаемые решения полностью не противоречивы, а также согласованы с требованиями качества управления и формами неопределенности.

Для решения подобных задач разрабатывается теория интеллектуальных систем управления (ИСУ). Одним из основных назначений и преимуществ эффективного применения ИСУ является возможность гарантированного достижения цели управления с максимальным качеством управления на верхнем уровне и минимальным расходом полезного ресурса системы «объект управления (ОУ) + регулятор» на нижнем (исполнительском) уровне иерархической САУ.

На содержательном уровне данная возможность отражает назначение целенаправленной деятельности ИСУ в общем случае непредвиденных ситуаций управления.

При этом эффективность применения ИСУ зависит от уровня интеллектуальности разработанной системы (формы, вида и глубинного представления знаний). Важную роль при формировании уровня интеллектуальности САУ играет выбор используемого инструментария технологии ИВ для проектирования соответствующей БЗ при заданной цели управления.

Динамическое поведение ОУ и системы управления (регулятора) служит источником объективных знаний для формирования БЗ, полнота (soundness) которой зависит от достоверности извлекаемой из конкретного источника информации.

Неточность (imperfect) измерения (обусловленная объективной природой объекта) и недостоверность (unreliable) представления извлекаемой информации (например, из-за присутствия человеческого фактора в контуре управления) приводит к повышению информационного риска и возникнове- нию непредвиденных ситуаций управления, компенсация которых для обеспечения робастности управления осуществляется применением необходимого уровня ИВ.

В фиксированных ситуациях управления НР с БЗ (спроектированные с помощью оптимизатора БЗ – ОБЗ) обладают повышенной робастностью, соответствующие законы управления содержат меньше избыточной информации, используют минимальное количество датчиков и исходной информации и способны реализовать элементы самоорганизации поведения ОУ в непредвиденных ситуациях управления [18].

Следует подчеркнуть, что наличие избыточности информации в законах управления является физической объективностью, которая присутствует вследствие использования в процессах оптимизации БЗ случайного поиска в виде ГА, а также следует из законов теории информации о необходимости наличия избыточности в ненадежных каналах передачи данных с помехами.

Этот факт является неизбежной платой за возможность получить решение задачи оптимального управления существенно-нелинейными ОУ в условиях неопределенности исходной информации и многокритериальности условий оптимизации.

2.    Проблемы разработки ИСУ и технология мягких вычислений

Одной из трудностей разработки ИСУ для непредвиденных ситуаций управления и в условиях информационного риска является решение проблемы проектирования соответствующей БЗ, использующей объективные знания [19] о поведении ОУ и нечетких гибридных ПИД-регуляторов. Поэтому одной из сложных и ключевых проблем разработки основы информационной технологии проектирования ИСУ для такого широкого класса ОУ является процесс извлечения объективных знаний. На их основе осуществляется реализация этапов проектирования робастных БЗ в непредвиденных ситуациях управления для исполнительного уровня иерархической структуры управления, учитывающего в продукционных правилах БЗ реальные физические и информационные ограничения. В частности, в качестве информационных ограничений рассматриваются информационные оценки приращения риска, которые учитываются в части логической посылки «Если…» продукционных правил «Если А, То В» (см. ниже п. 3.1).

Взаимосвязи вопросов корректности (неточности) описания моделей ОУ и роль технологии ИВ рассмотрим на примере решения задач робастного интеллектуального управления на основе технологий мягких вычислений.

• 2.1.    Технология мягких вычислений

C точки зрения применения в системной инженерии технология мягких вычислений базируется на двух основных идеях: (1) на обобщении понятия числа путем введения качественной (лингвистической) шкалы, что привело к созданию нечетких множеств, нечетких чисел и лингвистических переменных с соответствующими операциями над ними; и (2) на введении понятия нечеткого логического вывода, что привело к созданию нечеткой логики с различными моделями нечеткой импликации и продукционных правил.

Обобщение понятия числа происходит за счет введения новой (субъективной) качественной шкалы и отображения в нее с помощью функции принадлежности (ФП) лингвистической аппроксимации его количественной характеристики.

Типовые ФП ц _А ( д ') , представляющие нечеткое множество А, приведены на рис. 4.

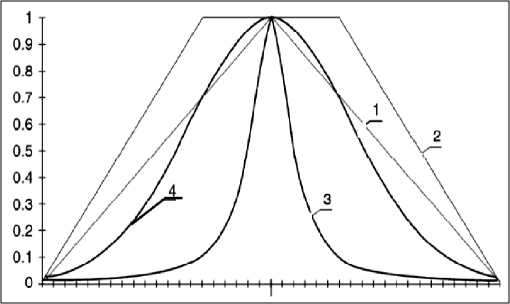
Рис. 4. Типы функций принадлежности:

1 – треугольная; 2 – трапецеидальная; 3 – Белла; 4 – гауссовская

ФП определяют степень достоверности принадлежности элемента x е X нечеткому множеству {ц _А ( x ) > 0, x е X } . Более точно, пусть X есть некоторое универсальное множество (универсум). Тогда нечеткое множество А в X определяется как упорядоченное множество пар ^А = { ( x , M a ⁽ x ))| x ^е X } , где m a ( x ) е [0,1] называется ФП элемента х к нечеткому множеству А .

ФП приписывает каждому элементу из Χ значение из интервала [0, 1], которое называется степенью принадлежности х к Α или нечеткой мерой. Поэтому нечеткая мера может быть рассмотрена как степень истинности того, что элемент х принадлежит Α . Более точные определения возможны на основе аксиоматика t-норм и t -конорм, традиционно применяемых в нечеткой логике.

Пример типовых ФП величины напряжение в виде лингвистической аппроксимации «низкое – low», «среднее - medium» и «высокое - high» на количественной шкале [ 0 100 ] показан на рис. 5.

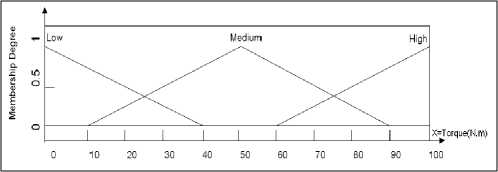
Рис. 5. Пример функций принадлежности лингвистических переменных «низкое – low», «среднее – medium» и «высокое – high» усилие

Отметим, что такие ФП описывают т.н. нечеткие множества 1-го рода.

Для расширения возможности описания неопределенности в лингвистических переменных вводятся ФП нечетких множеств 2-го рода [20], представленных на рис. 6.

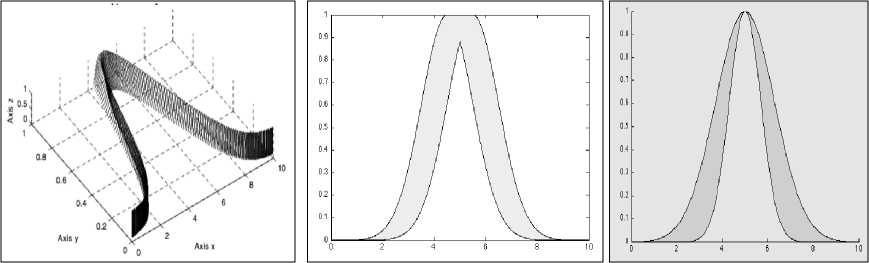
а                                   б                             в

Рис. 6. Функции принадлежности нечетких множеств 2-го рода; а – 3-мерное представление;

б – гауссовская ФП с мерой неопределенности (1); в – гауссовская ФП с мерой неопределенности (2)

Так для описания на рис. 6,б применяется ФП вида:

и

Ца ( x ) = exp <

x

σ

m g [ m 1 , m 2 ]

Ца (x ) = exP ’

x

σ

ст e^,ст2]

для представления ФП на рис. 6,в.

Одним из основных отличий нечетких множеств является наличие нестандартных операций над ними, которые позволяют осуществлять гибкие интерпретации над результатами их применения, например, в моделях нечеткого логического вывода. На рис. 7 приведен пример нестандартной операции отрицания A = — A ^ ц ^ ( x ) Сугено с ФП следующего вида:

Цу (x ) =

1 + Лца (x) ’

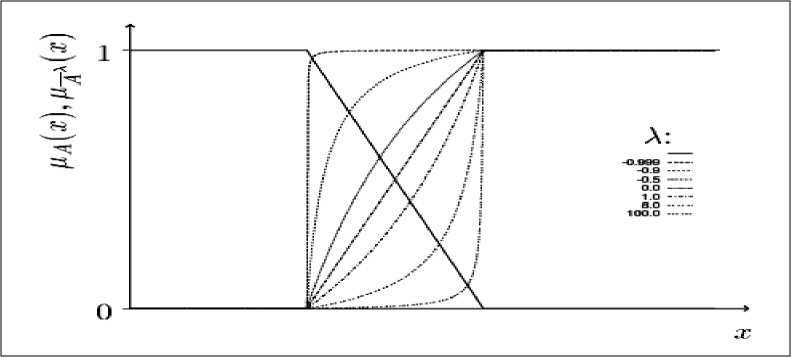
Рис. 7. График ФП отрицания Сугено

В зависимости от значения параметра λ можно усилить или ослабить отрицание, что невозможно в булевой логике.

На рис. 8 показана ситуация, в которой не выполняется закон исключения третьего.

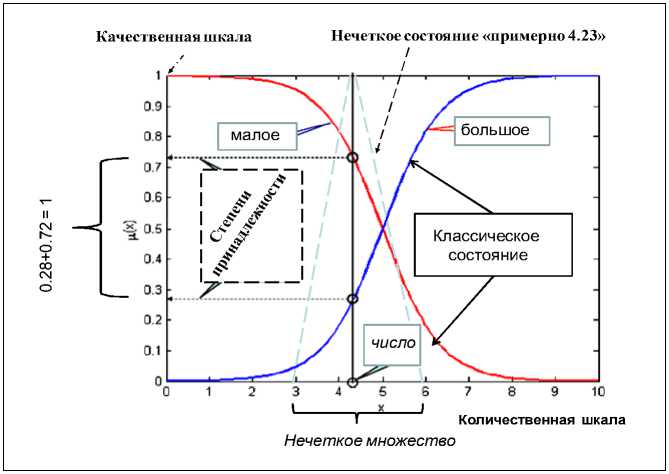
Рис. 8. Иллюстрация не выполнения в нечеткой логике закона исключения третьего

Конкретному состоянию (сингелтон) в виде числа 4.23 (одновременно «приблизительно 4», например, с треугольной ФП) на интервале [0, 10] числовой шкалы измерений соответствуют две лингвистические переменные «большое» и «малое» число со степенями принадлежности на качественной лингвистической шкале 0.28 и 0.72 (0.28 + 0.72 = 1) соответственно.

В этом случае нечеткое состояние «приблизительно 4» в виде 4.23 характеризуется двумя лингвистическими переменными «большое» и «малое» число и позволяет расширить возможности качественного описания количественной характеристики. Это приводит к нестандартному выводу о возможности одновременного рассмотрения, например, числа 4.23 на шкале [0, 10] как лингвистической переменной «большой» или «маленький» или «приблизительно 4» с различными значениями функции принадлежности на заданной качественной лингвистической шкале.

Однако, этот на первый взгляд парадоксальный факт в условиях существенной неопределенности исходной информации на практике привел к хорошим результатам.

• 2.2.    Модели нечеткого вывода

Рассмотрим основные модели нечёткого вывода, которые могут быть реализованы в ИСУ.

Правило нечёткого вывода в модели Мамдани имеет вид:

IF x1 is pj (x1) AND x2 is цj2 (x2) AND.. AND xn is pj. (xn) THEN y is ц*^, где l - номер правила; X1,.,Xn- входной вектор; цi - i -e терм-множество к -ой входной переменной, к g{1, ., n}, i g{1, ., mk }; цi,^+1 - i -e терм-множество выходной переменной; j^ -индекс, показывающий какое из терм-множеств k -ой переменной используется в правиле l . Результат нечёткого вывода в модели Мамдани определяется следующим образом:

F ^{( x} 1 , . x n ) =

ZMy-nj)

X M . n n = , ц к . ( X k )

где y _l – модальное значение нечёткого множества µ

n+1

• n + 1

; Π – используемая t-норма, М – число пра-

вил.

В модели Сугено правила имеют вид:

IF x, is Ц (x,) AND x2 is цj2 (x2) AND.. AND xn is ц n (xn) THEN y is f (x1, _, xn),

l где f – некоторая функция входного вектора. Результат нечёткого вывода в этой модели определяется по формуле:

F ⁽ x , , . x _n ) =

E м fl(xi,., xn )П n—1 ц.(x) E МП i—, ^ (x.)

Как правило, при использовании модели Сугено, в качестве функций f рассматривают полино- мы. Так, в модели Сугено 0-го порядка эта функция имеет вид: f (x,,.,xn) — a0, а в модели Суге- но 1 -го порядка f (x1,., xn

) ^— E . _— 1 a k x k + a 0 .

На рис. 9,а,б представлены идеология построения нечетких систем и логическая структура нечеткого регулятора соответственно.

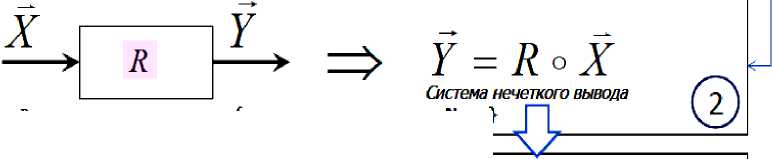
R - нечеткое отношение:{тип нечеткого вывода, М,п,ц}

GAp оптимизатор базы данных

Выбор типа нечеткого вывода

Оптимизация числа правил

Оптимизация числа лингвистических переменных(п)

Оптимизация типа функции принадлежности (ц)

Оптимизатор БЗ на мягких вычислениях

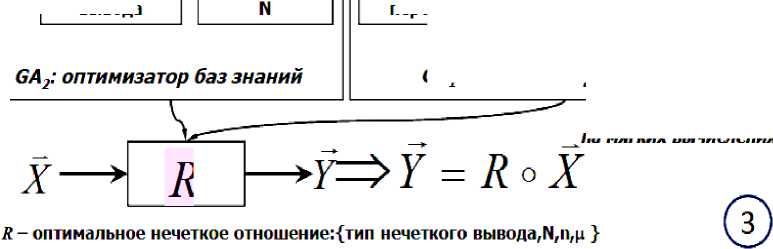
(а)

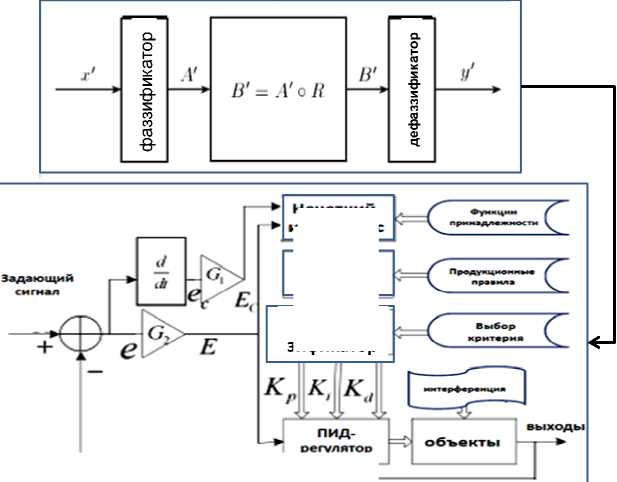
Нечетким интерфейс

Нечеткая логика

Дефаз-

(б)

Рис. 9. Идеология построения нечетких систем (а) и логическая структура нечеткого регулятора (б)

Структура моделей нечеткого вывода показана на рис. 10.

Антецедентная часть правила логического вывода Применение Т-нормы: Произведение или мин

Hi

Консеквентная часть правила логического вывода

Тип 1

Тип 2

Тип 3

Тип 4

zt = fi(*y)

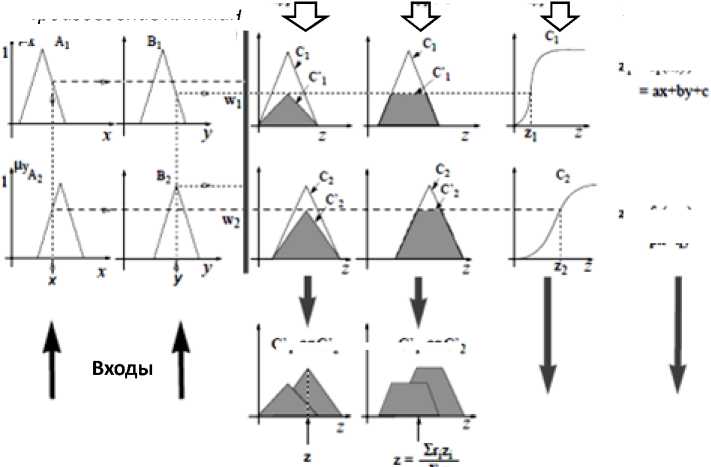
С , ОГС 2

С ;ОГС ,

Центр гравитации

Средне максимальное

_ W1Z] * W1Z2 Wj ♦ W2

Метод

Цукамото

_ w 1z 1 * w 2Z2 W] ♦ W2

Средне взвешенное

Xi ■ Ь(х.у) = px*qy*r

Рис. 10. Структуры моделей нечеткого вывода

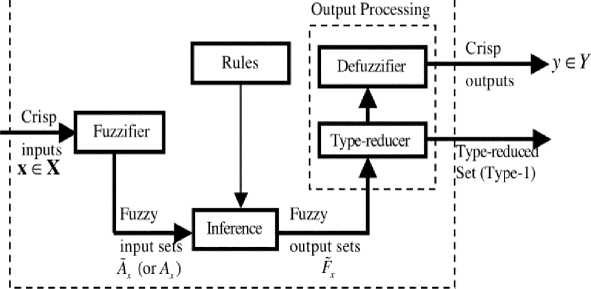
Структура нечеткого регулятора и модель нечеткого логического вывода для нечетких множеств 2-го рода приведены на рис. 11.

Type-2 FLS

(а)

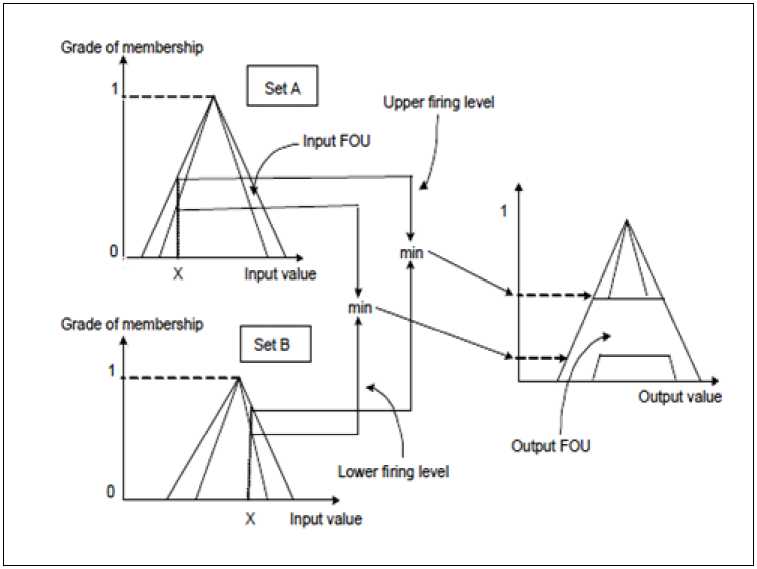
(б)

Рис. 11. Структура нечеткого регулятора (а) и модель нечеткого логического вывода (б) для нечетких множеств 2-го рода

В дальнейшем по тексту под термином БЗ понимается стандартное для теории нечетких систем управления определение БЗ в виде конечного множества продукционных логических правил (look-up table) определенной модели нечеткого вывода с конкретными типами и параметрами ФП, формирующих законы управления ОУ. Параметры и тип ФП хранятся в базе данных НР. В реальных системах нечёткого вывода допускается наличие нескольких выходных переменных, значение каждой из которых определяется независимо друг от друга.

Отметим следующие особенности, которые можно наблюдать на примере этих моделей:

Вид предпосылки правила не зависит от модели нечёткого вывода и определяется только индексами выбранных для данного правила терм-множеств. Множество всех правил образуется декартовым произведением терм-множеств всех переменных и число правил M = ^ ^ ^ k •

Вид заключения правила зависит от используемой модели нечёткого вывода, при этом некоторые модели используют терм-множества для выходных переменных, а некоторые – не используют.

Для расчёта результата нечёткого вывода всегда необходимо вычислять значения nn .Л

µ (x ) , которые будем называть уровнем активации правила l . При этом, правила с нуле-i =p j вым уровнем активации не оказывают влияния на результат.

Вычисление результата нечёткого вывода может быть организовано, как процесс накопления частичных результатов, вычисляемых для каждого активированного правила.

• 2.3.    Принципы и отличия построения нечетких систем управления на основе мягких вычислений

Здесь опишем схематично основные принципы и отличия построения нечетких систем управления на основе мягких вычислений (подробности приведены в [19]).

Нечеткие модели логического вывода на фазовом пространстве лингвистических переменных позволили разработать нечеткие ИСУ, эффективно решающие задачи управления в условиях существенной неопределенности исходной информации, слабой формализации описания ОУ, нечеткости целей управления, и т.п.

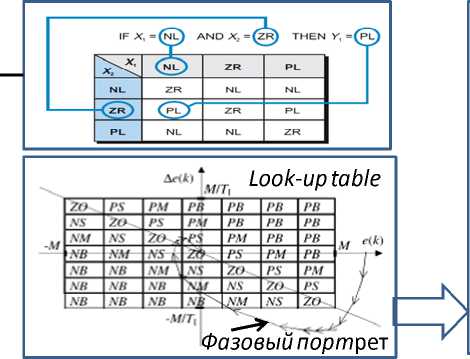
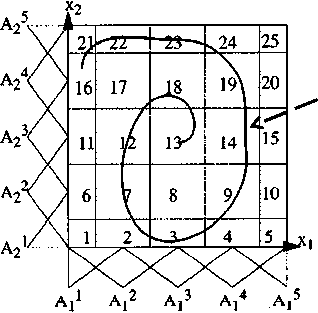
На рис. 12 схематично показана основная идея построения фазового портрета лингвистических переменных, отражающих качественные особенности динамических характеристик ОУ.

Одним из основных результатов теории нечетких систем для теории и систем управления является теорема о наличии универсального аппроксиматора, утверждающая существование возможности аппроксимации сложных слабоструктурированных ОУ конечным числом продукционных правил в БЗ в виде нечеткого регулятора [19-22].

Однако алгоритма определения такого (необходимого и достаточного) конечного числа продукционных правил не установлено и в этом смысле теорема не конструктивна.

На рис. 13 показана схема решения задачи определения необходимых параметров универсального аппроксиматора на основе оптимизатора БЗ (ОБЗ) на мягких вычислениях.

ос

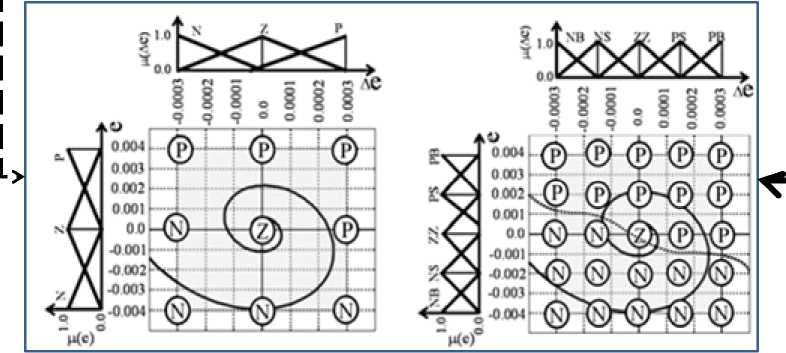
Рис. 12. Фазовый портрет лингвистических переменных

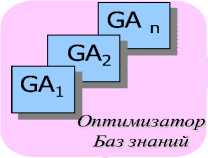
KB

IF'11 х, is ,4}” and ...x^is^'1'

N< IF"¹ x, is Л,¹'¹ and ...x„ is Л"¹

IF'™ x, is Л,¹™¹ and ...x„ is 4'™

tlienj-'¹¹ = f^u(x,.....x„) theny» = /"'(x„...,xJ then/™ = f^w(x_v...,x„)

n

Type of Fuzzy Inference

База знаний

Нечеткий регулятор

Универсальный аппроксиматор

Рис. 13. Структурная схема определения параметров универсального аппроксиматора на основе ОБЗ

Существует однозначное соответствие между структурами нечетких регуляторов и нечетких нейронных сетей (рис. 14).

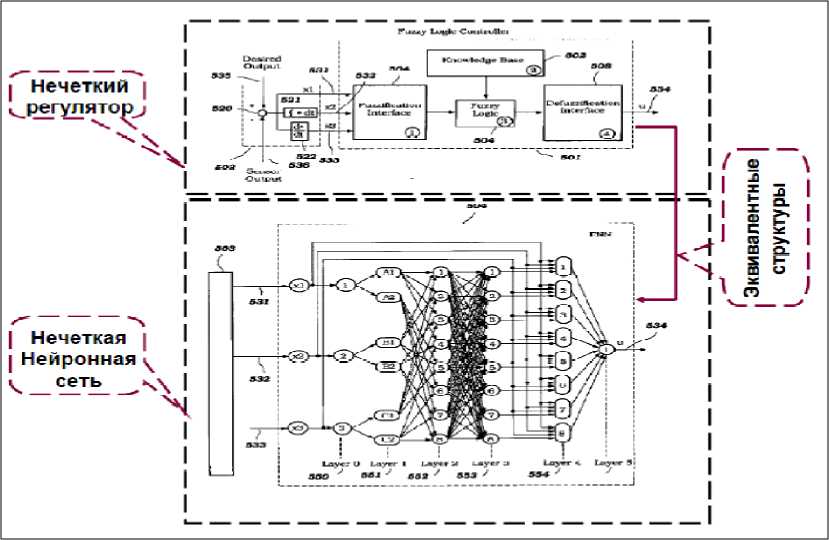
Рис. 14. Соответствие между структурами нечеткого регулятора и нечеткой нейронной сети

Данные определения и их применения в интеллектуальных НР на основе ОБЗ на мягких вычислениях рассмотрены в [19].

Одной из основных проблем эффективного применения технологии мягких вычислений в задачах управления являлось решение следующих задач:

• -    объективное определение вида ФП и ее параметров в продукционных правилах в БЗ;

• -    определение оптимальной структуры нечетких нейронных сетей в задачах обучения (аппроксимация обучающего сигнала с требуемой (заданной) ошибкой и с минимальным количеством продукционных правил в БЗ);

• -    применение генетического алгоритма (ГА) в задачах многокритериального управления.

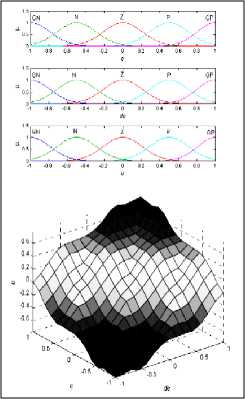
Так, например, на рис. 15 показано влияние выбора числа и вида ФП на вид поверхности нечеткого вывода [23], которые оказывают существенное влияние на решение первой из указанных выше проблем.

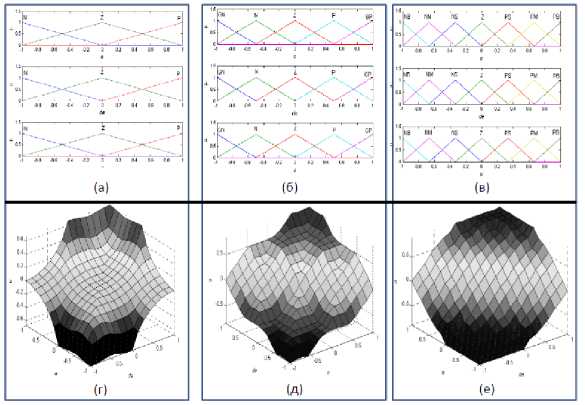
Рис. 15. Влияние числа (а) – (е) и вида (справа) ФП на вид нечеткого вывода

На рис. 16 показан результат влияния ассимметрии ФП на вид поверхности нечеткого вывода.

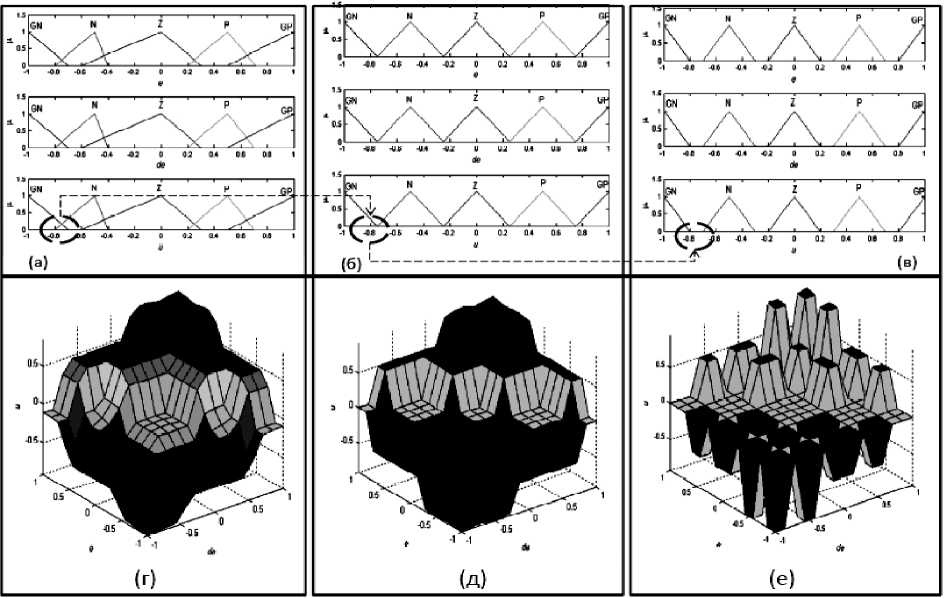
Рис. 16. Влияние ассимметрии ФП на вид нечеткого вывода

Перечисленные проблемы были решены и апробированы на основе Оптимизатора Баз Знаний (ОБЗ) с применением технологии мягких вычислений [24-26]. Разработанный интеллектуальный инструментарий позволил проектировать робастные БЗ на основе решения одной из алгоритмически трудно решаемых задач теории искусственного интеллекта – извлечения, обработки и формирования объективных знаний без использования экспертных оценок.

В данном оптимизаторе используются три ГА, которые позволяют спроектировать оптимальную структуру нечеткого регулятора (вид и число ФП, их параметры, а также число самих правил нечеткого вывода), аппроксимирующей обучающий сигнал с требуемой ошибкой.

Объединение методологий стохастического и нечеткого моделирования ИСУ в инструментарии ОБЗ позволило повысить уровень робастности проектируемых БЗ и решать сложные задачи формирования объективных знаний.

3.    Структура ОБЗ и шаги оптимизации БЗ с учетом приращения информационного риска

Оптимизатор БЗ на мягких вычислениях является новым эффективным программным инструментарием построения БЗ робастных ИСУ с использованием новых критериев оптимизации в виде новых типов функций пригодности ГА (рис. 17) [19, 26]. В качестве таковых используются термодинамические и информационно-энтропийные критерии. Входом ОБЗ является обучающий сигнал, который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, т.е. непосредственно из измерений динамических параметров физической модели ОУ.

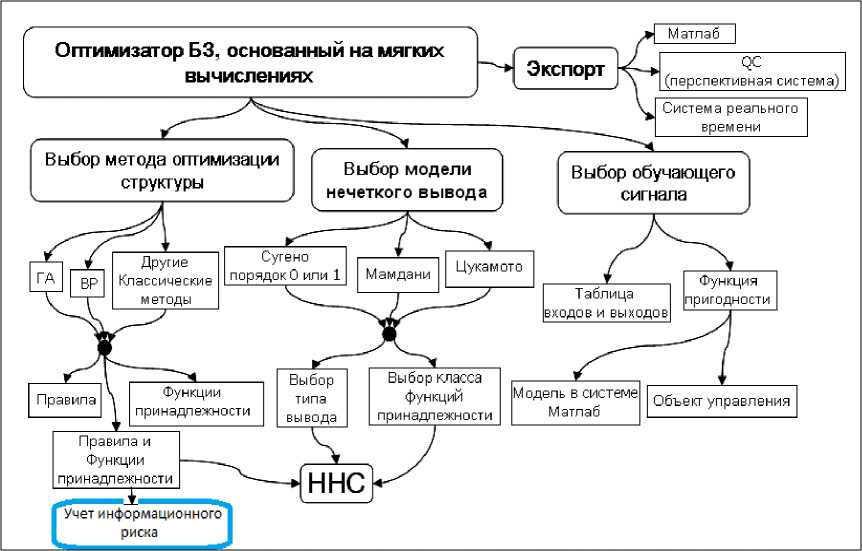
Рис. 17. Структура ОБЗ с новым блоком описания информационного риска

Следует подчеркнуть, что управляющее воздействие, формируемое при наличии сигнала, определяется степенью близости оценки и истинного значения параметра. Ошибки при этом могут порождаться как некорректностью идентификации сигнала, так и неточностью его оценивания. Решение задачи совместной идентификации и оценивания параметров сигнала при параметрической априорной неопределенности и ограничении сверху возможного числа наблюдений можно получить за счет применения адаптивного байесовского подхода к наблюдениям.

При этом общее и доступное число наблюдений в практических задачах идентификации ситуации управления и оценки ее наиболее информативных параметров всегда ограничено, что приводит к потере информации и опасности возрастания приращения информационного риска.

В связи с отмеченными фактами, рассмотрим математическую модель [19, 27] оценки приращения информационного риска для указанных условий функционирования ОУ как задачи о различении сложных гипотез.

• 3.1.    Математическая модель оценки приращения информационного риска

Рассмотрим типовую ситуацию идентификации слабо формализованной модели структуры ОУ в виде случайных параметров x = ( x 1,..., x n ) в присутствии (мешающего или маскирующего) параметра θ . Допустим, что экспериментально (в статистическом смысле) для вектора измеряемых случайных величин x = ( x 1, ^ , x n ) и неизвестного параметра 0 определена функция плотности распределения вероятностей параметров модели в виде p ( x , 0 ) (аппроксимирующая в общем случае неизвестную истинную функцию p ( x , 0 ) ).

Информационное расхождение (дивергенция) между функциями распределения вероятностей определяется мерой Кульбака-Лейблера в виде:

I ( ^p : ^p MJ ^p ( ^x , ⁰ ) ln pgl

dxd θ .

По заданным функциям потерь W(W) и распределения вероятностей p(x,0)[p(x,0)] вычис- ляется усредненный риск в виде: r

( W ² ) ( r ( W ² ) ) = {[ W ² p ( x , 0 ) dxd 0 ( jj W ^ ² p ( x , 0 ) dxd 0 ) .

Тогда информационная оценка приращения риска (снижения точности определения параметров модели ОУ из-за редукции аппроксимации истинной функции плотности распределения вероятностей, как меры корректности модели) определяется следующим выражением [19, 27, 28]:

-r (W2) 21 (p : p) < (5 = r - r ) < ^r (W2) 21 (p : p). (4)

Таким образом, (верхняя и нижняя) оценка корректности модели в виде приращения риска ( 5 = r - r ) из-за редукции данных измерения при мешающих параметрах в процессах измерения носит нелинейный характер зависимости от информационной дивергенции – расхождения (меры информированности исследователя) оценок качества модели ОУ.

Приведенный результат означает, что исходного количества информации и интуитивного представления в виде информированности исследователя может оказаться недостаточным для формирования корректной модели ОУ, а сформированная модель содержит структурные элементы неопределенности.

Следовательно, интуитивный инженерный подход к разработке приближенных (расчетных) моделей ОУ, носящий зачастую вид линейной зависимости от количества извлекаемой информации о параметрах структуры ОУ, может привести к существенному расхождению в точности и с необходимым качеством формирования корректного описания модели ОУ [29].

Приведенный пример показывает, что помимо физических ограничений, на корректность описания и достоверность извлеченных знаний из модели ОУ существенное влияние оказывают также и информационные границы на применимость разработанной модели [30].

В теории и систем управления одним из эффективных подходов снижения риска принятия решения (от неполноты описания модели ОУ) является разработка структур робастных ИСУ.

Данные структуры реализуют принцип компенсации неопределенности описания модели ОУ за счет повышения уровня интеллектуальности традиционных систем управления.

В частности, компенсация информационной неопределенности осуществляется за счет повышения интеллектуальности нижнего исполнительского уровня в виде соответствующих структур интеллектуальных регуляторов и соответственно спроектированных (с учетом в продукционных правилах информационного риска) самоорганизующихся робастных БЗ.

Таким образом, реализация данного принципа обеспечивает робастность ИСУ при неполном описании модели ОУ за счет учета в продукционных правилах проектируемых БЗ неточной (imperfect), извлекаемой из данной модели, информации и самоорганизации БЗ.

Выбор корректной модели, в первую очередь ОУ минимальной алгоритмической сложности, является важной для практики задачей. Однако сам критерий минимальной алгоритмической сложности при выборе метода описания модели ОУ требует уточнения и физического обоснования.

• 3.2.    Этапы проектирования БЗ

Нами предложены следующие этапы построения БЗ ИСУ с помощью ОБЗ.

Этап 1. Определение типовой ситуации обучения (параметры математической модели ОУ; определение внешних шумов, начальных условий, ограничений и времени задержки).

Этап 2. Построение обучающего сигнала происходит на основе стохастического моделирования поведения ОУ в типовой ситуации, проведенного с использованием математической модели ОУ и генетического алгоритма (ГА) с выбранными критерием оптимизации и областью случайного поиска.

Этап 3. Выбор модели нечеткого вывода. Пользователь конкретизирует тип нечеткой модели вывода (Сугено, Мамдани и т.д.), операцию нечеткого И (произведение или минимум), число входных и выходных переменных. В нашем случае это модель Сугено. Пусть n ₁, n ₂, n ₃ есть количество функций принадлежности, описывающих ошибку управления е, ее скорость и интеграл, тогда общее число нечетких правил будет n 1 х n ₂ х n 3 .

Само нечеткое (продукционное) правило в БЗ с учетом информационного риска выглядит сле- дующим образом:

IF e is A1 and e is B1 and J edt is C1 and information risk Др is D1THENKp = Dm, Kd = Em, Ki = Fm, где A1 ,B1,C1,D1 – функции принадлежности, описывающие ошибку управления е, ее скорость и интеграл, а также приращение информационного риска.

Таким образом, структура самого продукционного правила не изменяется, а расширяется только левая часть правила за счет добавления новой ФП для описания параметра D ₁ , характеризующий степень приращения риска.

Конечный результат нечеткого вывода в заданной БЗ вычисляется по следующим формулам:

K p

n ₁    n ₂ n ₃

EEE ^Dijk

У i=1 j=1 k=1 J n1   n2 n3

EEE -

У i = 1 j = 1 k = 1       у

; Kd =

n ₁ n ₂ n ₃

EEE ® j_t E jk

У i=1 j=1 k=1 J n1 n2 n3

EEE -

У i = 1 j = 1 k = 1       J

; Ki =

n ₁ n ₂ n ₃ EEE ® jk F jk

У i=1 j=1 k=1 J n1   n2 n3

EEE - j.

У i = 1 j = 1 k = 1       J

где ® j_t = A i ( e) ■ B j (e ) ■ C k ( e ) ■ D, ( Д р )

« ∙ » – символ операции нечеткого умножения.

Этап 4. Создание лингвистических переменных для входных значений (ошибка управления, скорость ошибки управления, интегральная ошибка управления) НР. С помощью ГА определяется оптимальное число ФП для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления их ФП (треугольная, Гауссовская и т.д.). В качестве информационного критерия оптимальности той или иной конфигурации лингвистических переменных используется максимум совместной информационной энтропии и минимум информации о сигналах в отдельности.

На рис. 18 показан пример построения лингвистических переменных с помощью ОБЗ.

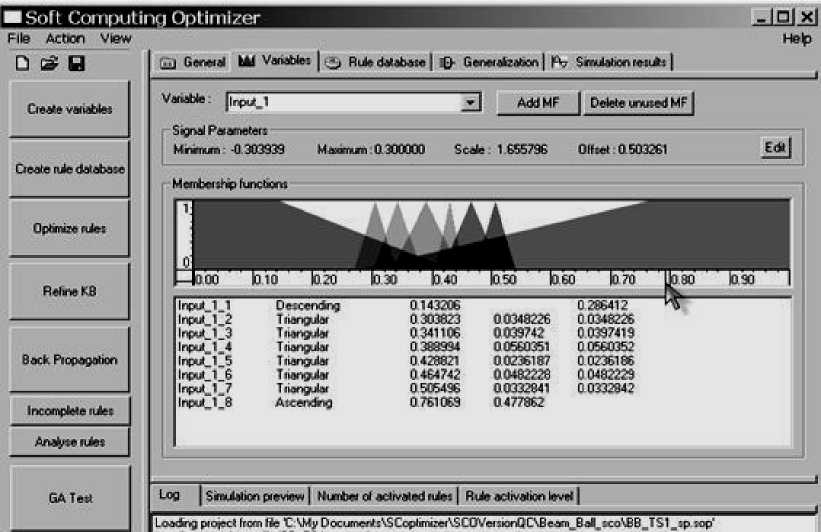
Рис. 18. Пример построения лингвистических переменных с помощью ОБЗ

Как видно из рис. 18 для описания входных значений ошибки управления ОБЗ с помощью ГА выбрал 8 ФП.

Этап 5. Создание, оптимизация и настройка базы правил. На данном этапе используется специальный алгоритм отбора наиболее «робастных правил» в соответствии с разработанными критериями. Кроме того, с помощью серии ГА находится оптимальная структура БЗ.

ОБЗ состоит из взаимосвязанных генетических алгоритмов (ГА1, ГА2, ГА3) [19, 21, 22], оптимизирующих отдельные компоненты БЗ (рис. 19).

Вкратце опишем их, согласно приведенным этапам проектирования.

Шаг 1: Выбор модели нечёткого вывода. Пользователь определяет тип нечёткой модели вывода и число входных и выходных переменных.

Шаг 2: Создание лингвистических переменных. С помощью ГА1 определяется оптимальное число функций принадлежности для каждой входной лингвистической переменной, а также выбирается оптимальная форма представления ее функций принадлежности.

Шаг 3: Создание базы правил. На данном этапе используется специальный алгоритм отбора наиболее «робастных правил» в соответствии с выбранными критериями.

Шаг 4: Оптимизация базы правил. С помощью ГА2 оптимизируются правые части правил БЗ.

Шаг 5: Настройка базы правил. С помощью ГА3 оптимизируются левые и правые части правил БЗ, т.е. подбираются оптимальные параметры функций принадлежности входных/выходных переменных с точки зрения заданной ФП. На данном этапе имеется также возможность настройки БЗ с помощью традиционного метода обратного распространения ошибки.

Итак, входом ОБЗ является ОС, который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, т.е. непосредственно из измерений динамических параметров физической модели ОУ. В частности, в качестве информационных ограничений рассматриваются информационные оценки приращения риска, которые учитываются в части логической посылки «Если…» продукционных правил «Если … То …» [19, 31].

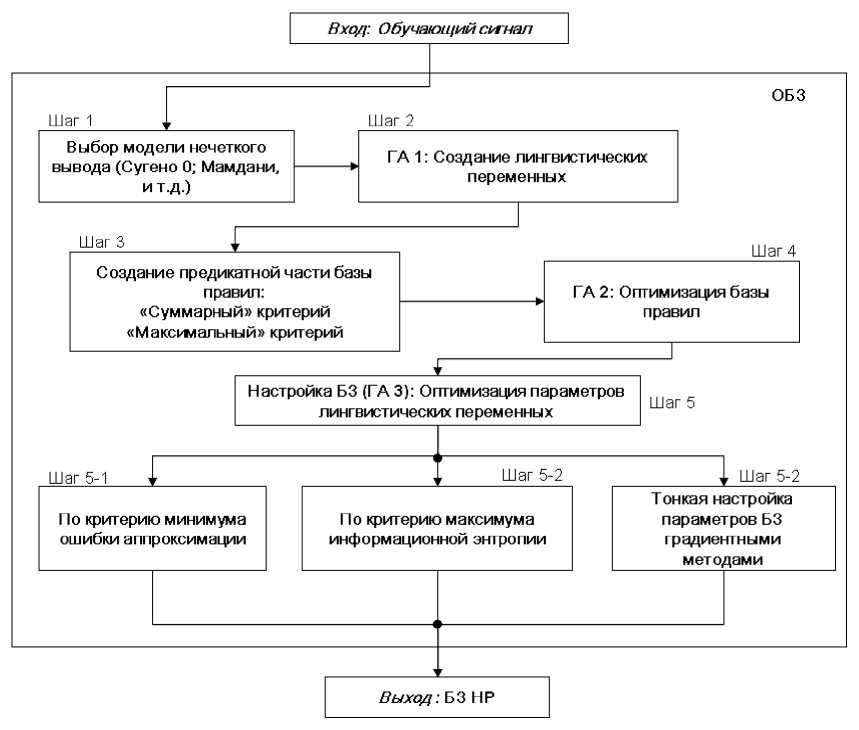
Рис. 19. Структура ОБЗ и шаги оптимизации БЗ

Например, рассмотрим традиционную структуру логического нечеткого вывода в виде продукционных правил «Если А То В», где А и В нечеткие лингвистические переменные. В НР лингвистические переменные А и В описываются соответствующим набором ФП. При этом структура логической посылки А записывается в виде:

∫ edt

Если ошибка е малая величина, скорость ошибки ė средняя величина и накопление ошибки средняя величина,

То параметры регулятора kp большая величина, kd малая величина, kI средняя величина.

Отметим, что в такой структуре оценка приращения информационного риска не учитывается.

В нашем случае структура логической посылки имеет следующий вид:

∫ edt

Если ошибка е малая величина, скорость ошибки ė средняя величина, накопление ошибки средняя величина, И степень приращения риска Δρ средняя величина,

То параметры регулятора kp средняя величина, kd большая величина, kI малая величина.

При этом информационная оценка риска Дс = Г — Г и определяется верхней и нижней границей информационных расхождений в (43).

На рис. 20 показан пример выбора лингвистической переменной для приращения риска.

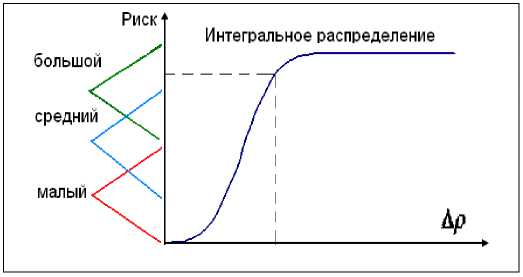
Рис. 20. Формирование лингвистических переменных в зависимости от величины оценки приращения риска

Выбирая с помощью ОБЗ (рис. 21) оптимальные ФП приращения риска в части Если А, осуществляем компенсацию риска в части То В.

Пример проектирования продукционных правил с учетом информационного риска представлен на рис. 21.

Традиционная структура продукционных правилЕ ели А То В

Если ошибка е .малая величина, скорость ошибки ё средняя величина и накопление ошибки | edt средняя величина,

То параметры регулятора к_р большая величина, кд .малая величина, kj средняя величина.

Структура с информационным риском Ар

Если ошибка е .малая величина, скорость ошибки ё средняя величина, накопление ошибки J" edt средняя величина, еличина.

То параметры регулятора к_р средняя величина, кд большая величина, комолая величина

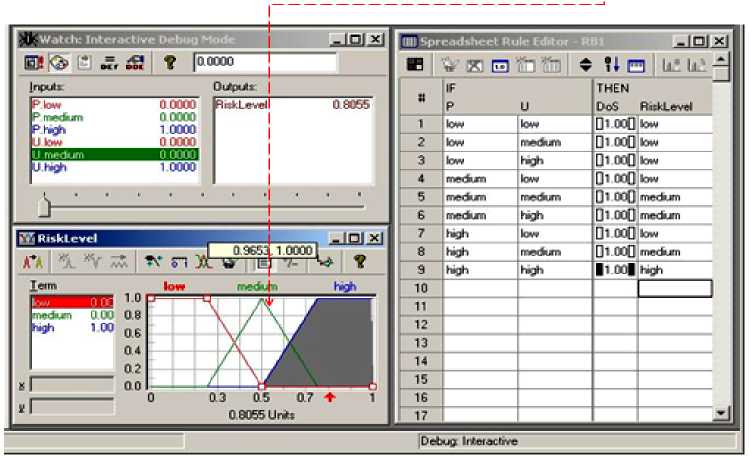
Рис. 21. Пример проектирования продукционных правил с учетом информационного риска

ОБЗ определяет оптимальные лингвистические переменные «большой», «средний», «малый». Следовательно, учет в продукционных правилах «Если А То В» величины приращения информационного риска в виде лингвистической переменной позволяет применить методологию проектирования БЗ на основе мягких вычислений с учетом информационных оценок приращения риска.

• 3.3.    Алгоритмы для оптимизации БЗ

Рассмотрим подробнее процесс оптимизации БП с помощью генетического алгоритма ГА2 (шаг 4).

(    i = M

Входом в данный блок является созданная на шаге 3 база правил (БП) { R. }    , где М - число

= 1

правил в базе для каждой выходной переменной. Для каждой выходной переменной правило R i имеет вид:

ЕСЛИ

e g A⁽ⁱ ) И e g B⁽ⁱ ) И J e g С⁽¹ ) И УРОВЕНЬ РИСКА D ^{( i} ) ^{s v} k

ТО

ЕСЛИ

sv'

входные переменные ННС e g A(1) И e g B(1) И J e g С(i) И УРОВЕНЬ РИСКА D(i) s'

ТО

ЕСЛИ

sv'

входные переменные ННС e g A(1) И e g B(1) И J e g С(i) И УРОВЕНЬ РИСКА D(i) s--V

v входные переменные ННС

ТО

кр* ) = nP* )

4----------v--'

выход 1 ННС

( i )               ( i )

D D

4----------v--'

выход 2 ННС

K<. ) = N( • ) ⁴----------v-- ' выход 3 ННС

где ( i ) – порядковый номер правила в базе прав и N _P , N _D , N _I – численные значения коэффициентов усиления ПИД–регулятора.

В соответствии со структурой рис. 19, на шаге 4 с помощью ГА2 оптимизируются правые части правил БП, определенной на шаге 3.

Функцией пригодности для данного шага служит минимум ошибки аппроксимации обучающего сигнала (ОС):

где E ₁ , E ₂ , E ₃ – суммарные квадратичные ошибки, вычисляемые для каждого выхода ННС (нечеткой системы вывода на основе нечеткой нейронной сети - ННС).

Эти ошибки вычисляются следующим образом.

• 1)    E , = ^ E , ( t k ) и E , ( t k ) = 1/2( F , (x , ( t k ), x ₂( t_fc ), x з ( t k )) - d , ( t k ))² ,

tk где x, = e; x2 = e; x3 = J edt - входные значения ННС и соответствуют значениям ошибки из ОС в момент времени t k и d1 – значение KP коэффициента усиления из ОС в момент времени tk ; и

M

У ^ - N < ^{г )}

iP z ™i i=1

где * - операция нечеткого умножения.

• 2)    E 2 = z E 2 ( t k ) , где E 2 ( t k ) = 1/2( F 2 (x , ( t k ), x 2 ( t k ), x 3 ( t k )) - d 2 ( t k ))² ,

tk где x1 = e; x2 = e?; x3 = J e, соответствует значениям ошибки из ОС в момент времени tk и d2 - значение KD коэффициента усиления из ОС в момент времени tk ; и

M

Z “ ND

У “                   ■ i=1

где * - операция нечеткого умножения.

• 3)    E 3 = Z E з ( t _t ) ,где E ( t_t ) = 1/2( F , (x , ( t_t ), x 2 ( t_t ), x ₂( t_t )) - d ₂( t_t ))² , t k

где x , = e ; x ₂ = e ; x ₃ = J e , соответствует значениям ошибки из ОС в момент времени t_k и d ₃ -значение K_I коэффициента усиления из ОС в момент времени t_k ; и

M iI

F 3 ( x , ( t k ), x 2 ( t k ), x з ( t k )) = -=4; -------, “ = A >” * B >” * C^{1, 1} * D "¹

У “,                          ■ i=1

где * - операция нечеткого умножения.

После того, как функция пригодности определена, рассматривается проблема кодирования.

Для ГА2 используется следующая структура хромосомы:

( / , 1 2 lзГ ^Х ( l , 1 2 1 3 ) i = ² ^ ( l , 1 2 1 3 ) = M , ^ ^    ^ ^      ^ ^

KP KD KI    KP KD KI       KP KD KI где (1, 12 13У=1 - бинарные строки, кодирующие значения правой части Kp, Kd , К/ правила номер

^ ^ ^

K P K D K I

, ( t = ,); ( 1 1₂ 1 ₃ ) i = ² - бинарные строки, кодирующие значения правой части K P , K_D , K I правила

^ ^ ^

KP KD KI номер 2 (i = 2) и т.д.

Далее можно запускать ГА, который находит решение, близкое к глобальному оптимуму (минимум ошибки аппроксимации ОС).

Рассмотрим задачу генетического алгоритма ГА3, используемого для тонкой настройки БЗ на шаге 5.

С помощью ГА3 оптимизируются левые и правые части правил БЗ, т.е. подбираются оптимальные параметры функций принадлежности входных и выходных переменных (с точки зрения заданной функции пригодности). В данном процессе оптимизации используются различные функции пригодности, выбранные пользователем.

На данном этапе имеется также возможность настройки БЗ с помощью традиционного метода обратного распространения ошибки.

4.    Пример применения ИТП ИСУ на мягких вычислениях с использованием инструментария ОБЗ

Применение разработанной технологи проектирования БЗ рассмотрим на традиционном для теории ИСУ примере.

Динамическая система « шарик – доска» (см. рис. 22) является весьма популярным и широко используемым примером (т.н. Вenchmark) для изучения моделей управления в теории и систем управления.

ОУ, показанный на рис. 22, представляет собой шарик, движущийся вдоль доски, ограниченной длины. Положение одной стороны доски жестко фиксировано, противоположная сторона соединена с электродвигателем, так что доска может наклоняться под действием приложенной к ней силы.

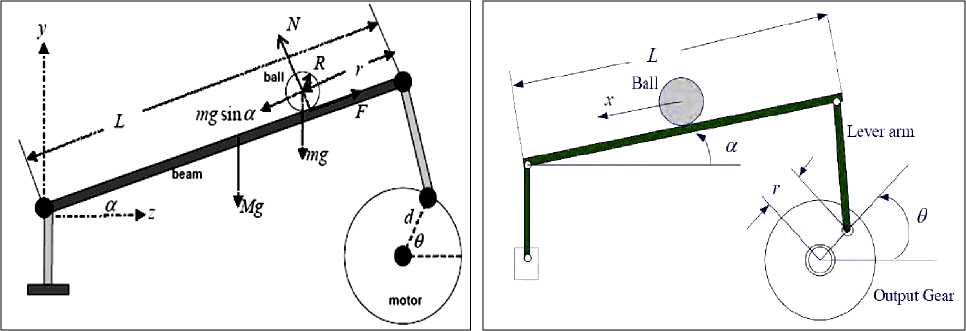
Рис. 22. Объект управления: динамическая система «шарик – доска»

Задачей управления является удержание (стабилизация) шарика в положении центра доски. При этом в ситуацию управления включены стохастические внешние воздействия, временные задержки в канале измерения состояния объекта и ограничения на максимальную силу управления и движения ОУ. Это сложная задача управления, так как шарик двигается с ускорением, нелинейно зависящим от угла наклона доски и находится в неустойчивом динамическом состоянии. Упрощенная математическая модель данного ОУ представлена следующими уравнения движения [32]:

б =

ф- 2тггб -

к

L . , )    .

mgr +— Mg cos б 2     7

J i + mr

• •r =

—

g sin

где б - угол поворота доски, б) - скорость изменения угла, б - ускорение изменения угла, соответственно; r – текущее положение шара – обобщенные координаты динамической системы; L – длина доски, M - масса доски, m - масса шара; J 1 = I a + ф , где I a - момент инерции доски (0.02 kg^ m ² ), I b - момент инерции шара (2х 10 ^{- 6} kg^ m ² ); N - сила трения; ф - сила управления.

Модели проведения реальных экспериментов [33-37] для данного ОУ представлены на рис. 23.

Рис. 23. Физические модели проведения экспериментов для рассматриваемого ОУ

Физическая модель доски представлена в виде двух равной длины поверхностей c различной шероховатостью. При управлении шарик может переходить с одной поверхности на другую, что создает неопределенность в отношении положения перемещения шарика по доске. Неровности поверхностей имеют одинаковую функцию плотности распределения вероятностей (равномерную) с разными дисперсиями, характеризующими высоту шероховатости поверхностей. При переходе с одной на другую поверхность необходимо оценить приращение информационного риска и его влияние на достижение цели управления.

Допустим, что о ( t ) – шум с равномерными функциями плотности распределения вероятностей и описывается в виде:

тогда приращение риска:

о ( t ) =

у2, 2L < r < L у., 0 < r < —L

Дс = у ₂ ² H ( б ), б = у^, H(б ) = | б ln б|

у ₂ ²

и H ( б ) описывает энтропийную меру неопределенности исходной информации о положении шарика на доске.

Выбирая с помощью ОБЗ оптимальные функции принадлежности приращения риска (который 2

зависит от отношения величин дисперсий б = —12- ) в части Если А, обеспечиваем компенсацию у ₂ ²

риска в части То В.

ОБЗ определяет оптимальные лингвистические переменные «большой», «средний», «малый» в виде, представленном на рис. 18.

На рис. 24 представлены результаты моделирования динамического поведения системы (5) при условиях (6) и (7).

ПИД

НР1

w*№^W4^

-20

>2

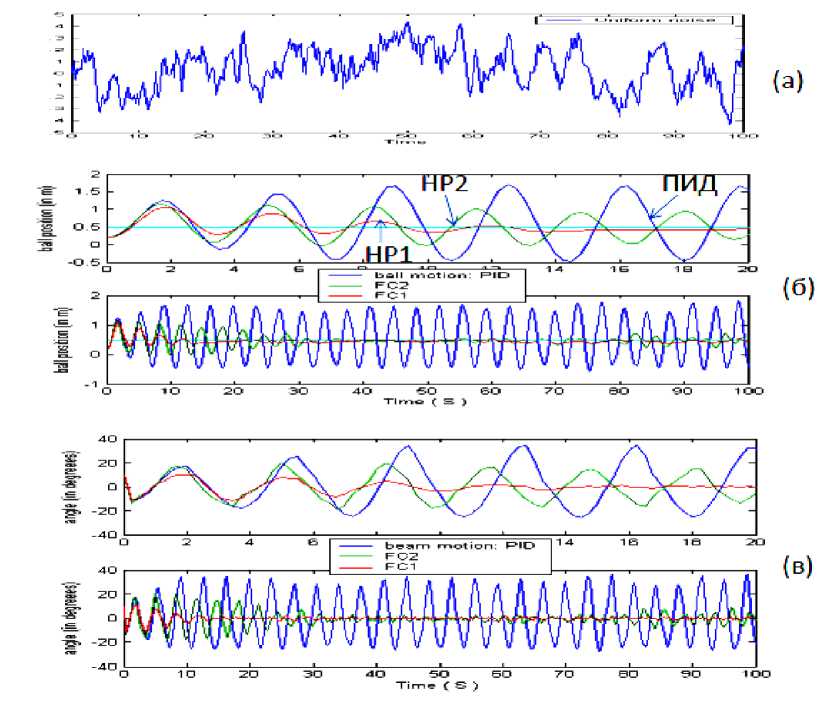
Рис. 24. Динамическое поведение системы «шарик – доска»

(а) – шум с различными дисперсиями; (б) – поведение шарика; (в) – поведение доски

На рис. 24 (а) представлена выборочная траектория неровностей поверхностей, согласно (6).

Динамическое поведение шарика как ОУ при переходе с одной поверхности на другую (см. рис. 24,а) представлено на рис. 24,б.

Применение ПИД-регулятора, как следует из рис. 24,б, не позволяет решить поставленную задачу управления; применение НР2 (FC2), БЗ которого была спроектирована без учета приращения информационного риска в продукционных правилах, также не приводит к достижению цели управления. Как следует из рис. 24,б, движение шарика к цели управления осуществляется значительно эффективнее и с меньшей потерей полезного ресурса при применении НР1 (FC1) с БЗ, учитывающей приращение информационного риска перехода с одной поверхности на другую, чем при управлении НР2 с БЗ без учета соответствующего риска и при управлении ПИД-регулятором.

На рис. 24,в показано динамическое поведение угла поворота доски. Сравнение результатов моделирования БЗ без/с учетом риска позволяет оценить предельные возможности робастности проектируемых БЗ.

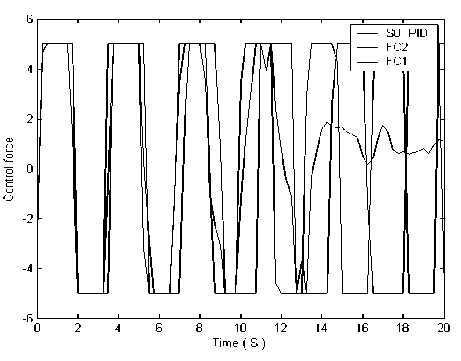
Расход полезного ресурса (см. рис. 25) оценивался в виде затрачиваемой управляющей силы и точности управления (ошибки управления и среднеквадратичной ошибки управления).

(а)

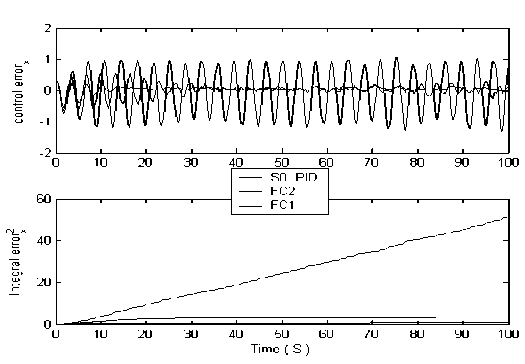
(б)

Рис. 25. Качество управления и расход полезного ресурса в системе «шарик – доска»: (а) – управляющая сила; (б) – точность управления

Представленная в даной работе технология проектирования БЗНР принципиально отличается от результатов работ [38-56].

Таким образом, добавление в логическую посылку ЕСЛИ продукционных решающих правил лингвистических переменных учета оценки приращения информационного риска в виде энтропийных оценок изменения статистического ансамбля событий дает возможность повысить надежность работы интеллектуального НР как исполнительного устройства, функционирующего в условиях непредвиденных (нештатных) ситуаций управления и неопределенности исходной информации.

Следовательно, НР1 является робастным в новой ситуации. ПИД и НР2 не справляется с задачей управления (шарик слетает с доски). НР1 показывает лучшее качество управления.

Заключение

Разработанный метод проектирования структур нечетких регуляторов на основе робастных БЗ, включающих в себя информационный риск, позволяет увеличить жизненный цикл работы ОУ и уменьшить расход полезного ресурса как ОУ, так и нечеткого регулятора.

Показано, что нечеткие регуляторы, основанные на традиционных инструментариях мягких вычислений, в которых структура нечеткой нейронной сети строится вручную экспертом, уступают в качестве управления и робастности нечетким регуляторам, учитывающим неопределенность исходной информации.

Полученные результаты позволили продемонстрировать эффективность нечетких регуляторов, как в типовых ситуациях управления, так и в широком классе нетиповых ситуаций, характеризующихся неопределенностью исходной информации.