Проектирование H-плоскостного ступенчатого сочленения двух прямоугольных волноводов

1. Расчет коэффициента отражения

Рассмотрим несимметричное H-плоскостное сочленение двух прямоугольных волноводов, изображенное на рис. 1, полагая заполнение кусочно-однородным. На интервале от z = _—м до z = 0 располагается волновод шириной a 2 , за- (1)    (1)

полненный средой с параметрами б' , ц' . В сечении z = 0 ширина волновода скачком меняется до размера a ₂, который сохраняется неизменным при z >  0. Более широкий волновод запол- (2)    (2)

нен средой с параметрами б , ц .

Волна основного типа, у которой Ey = e iYo z x п x x sin —, распространяется слева направо, Количество распространяющихся мод при z > 0 зависит от величин a 1, a2 и б(1), б(2), ц(1), ц(2). Для простоты будем считать, что в каждом из волноводом возможно распространение только основной волны с коэффициентами распространения (i = 1,2)

( i )

^Y 0 =

к ² б ⁽ i ) ц ⁽ i ) — ^ ) a ²

Из уравнений Максвелла можно выразить

магнитные составляющие поля через электриче-д ские, учитывая, что — = 0:

нХ' ) =

1 д E yi ) i юц ⁽ i ) ^д z

Разложение электрического поля по модам при z <  0 записывается в виде [1,2]:

E y

e - i ^^z + R 1 e i ^^z

м rmz . mпx

R m e m ^z sin-----,

a m=2                1

. п ж . sin— + a1

Vmn ii⁽¹⁾fJ⁽¹⁾ — 7-v⁽¹⁾ p i ^Y() z _i_ p i^{Y Y}() z у i ^Ц 0 Ц н_ж = i Y 0 — e    + R 1 e     x

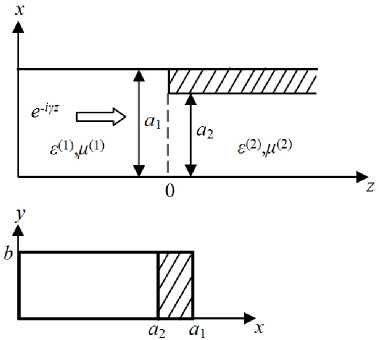
Рис. 1. Ступенька в Н-плоскости

x sin П Х + У R m r m e ^rSz sin m i x , a 1    mi 2                 ^a 1

где через R обозначен коэффициент отражения.

Постоянная распространения m -ой моды в 1-й области

г

2 (1) (1) б ц .

При z >  0 необходимо выделить слагаемое с коэффициентом прохождения T ₁ соответствующим T ₁ соответствующим распространяющейся волне[3]:

е У 2) = T 1 e^i Y q²⁾ z sin ^ x + y                  a ₂

to

+ Z Tme m=2

<²> . m п x

^{1 m} sin------, a ₂

(2) (2)        (2)

i ЮЦ о Ц H x = i У 0 T 1 ^e

i Y 0²) z sin ^ x — 2

to

— Z Tmrmermz sin m^x, a m=2                  2

где

=      J v(2) ц(2) Г	п x T 1 sin--- a 2	2 i iZ п Z„ m = 2	(2) rm- х m
. m п x х sin-----	a 2 J e '( x ') cos 0	m п x '	dx ' | .
a 2		a 2

(2) m

m п

Дифференцируя последнее уравнение по координате x , умножая его на функцию e '( x ) и интегрируя от 0 до a 2 имеем:

N I a 2

—

2 (2) (2) о ^ .

Обозначим через e ( x ) = E^ ( x , z = 0) напряженность электрического поля в сечении z = 0. При a 1 <  x <  a 2 эта функция равна нулю. Тогда используя граничные условия (ГУ) при z =0

Е У 1) = E y ²) = e ( x ),    И ® = H x ²⁾ = h ( x )

и используя свойства ряда Фурье, на отрезке [ 0, a 1 ] , можно записать [3]

y 0 ¹⁾ (1 — R 1 )

(1 + R 1 )

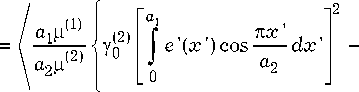
to

— i Z r m2) m = 2

a ₁

J e '( x ') cos

_____ T m п x

dx '

—

a ₂

2 ^{a 1}

1 + R 1 =       e ( x ) sin

a

п x ' .

dx , a ₁

a ₁

Rm =     e (x )sin a 10

to a 1

— i Z r m J e '( x ') cos m = 0      _ 0

m п x '

dx a1

dx '

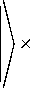
— 2

х

( m >  2).

Интегрирование по частям в правой части уравнения (3) дает, учитывая e'(x) = — e(x)

dx

e '( x ') cos      dx '

a

2 ^{a 1}

1 + R 1 = — f e ( x ) п

2 ^{a 1}

R m = e ( x ) m п

^п x ' cos dx , a ₁

m п x' cos a1

( m >  2).

Аналогично, на отрезке [ 0, a 2 ] следует

2 ar2

T1 = — f e (x ) cos

п

a ₂

T m = — f e '( x ') m п

( m

> 2).

m п x ' cos dx '

a ₂

Подставляя выражения (3), (4)

в соотноше-

ния для напряженности магнитного поля (1), (2) и приравнивая их в плоскости z = 0, получаем (0 <  x <  a 1 )

1 J                п x 2 i     Г ⁽ 1 ⁾

h0^{1)(1 —} R ^sin — + — Z   m х

Ц ⁽¹⁾ I               ^a 1 ^п m= 2 ^m

a 1

. m п xm х sin e (x ) cos a10

Последнее соотношение есть стационарный функционал относительно малых приращений функции e '( x ). Обозначив правую часть соотношения (6) через переменную F = F ( a 1 , a 2 , ц ⁽¹⁾, ц ⁽²⁾, Б ⁽¹⁾, б ⁽²⁾ ), получаем формулу для коэффици-

ента отражения

R 1 =

Y 01) — F

Y 01) + F ’

где F – выражение для правой части соот-

ношения (7), получаемой при подстановке в нее приближенного значения e ' (например, e '( x ) = A cos ^ x , где A — постоянная).

a ₂

Введем обозначения

F =

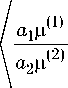
to

— i Zrm m=2

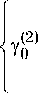
e '( x ')cos -^ x dx' a

a ₂

J e '( x ') cos

_____ T m п x

dx '

a ₂

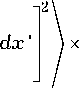
X

a ₂

j e '( x ')

n x '

cos dx '

a ₁

.

I i =

a 2 j 0

² n x , cos — dx ; a 2 J

I 2 =

a ₂ j 0

n x cos cos a2

m n x .

dx ;

a ₂

I 3 =

a ₂ j 0

n x cos cos a2

m n x .

dx ;

a ₁

1 4 =

a ₂ j 0

n x

n x

a ₁

a ₂

Интегралы, приведенные выше, вычисляются

точно и имеют следующее значение:

I i = a f ;   I 2 = 0;

I aa |   | a^m - a )

I3 = I                    I sin I 2-

( 2n(a2m - ai))    (   ai

+ |       ^a 1 a 2        | • | a 2 m + ^a 1 | .

(2n(a2m + ai))    (    ai

I 4 =f a i a 2 I sin I ( O L - O S ) ™ ) ₊

• ( 2 n ( a i - a 2 ) )    ( a i )

• + ( a i a 2 I sin ( ⁽ a i + a 2 ^{) n} |

• ( 2 n ( a i + a 2 ) )    ^ a i )

• 2.    Проектирование ступеньки в среде Microwave Studio

Подставляя значения интегралов в формулу (7), были вычислены значения коэффициента отражения при различных размерах ступеньки, учитывая, что ц ⁽¹⁾ = ц ⁽²⁾ = i. Результаты расчета приведены ниже.

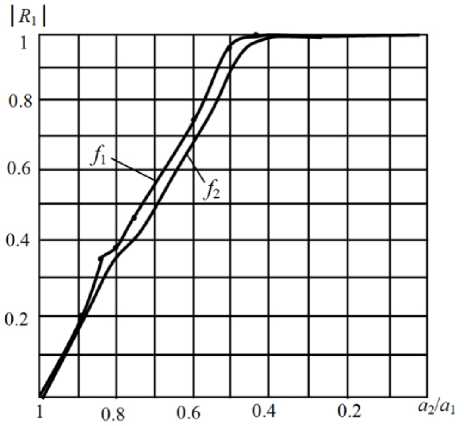
Рис. 3. s ⁽¹⁾ = е ⁽²⁾ = 10, Л = 10 ГГц, f 1 = 22 ГГц

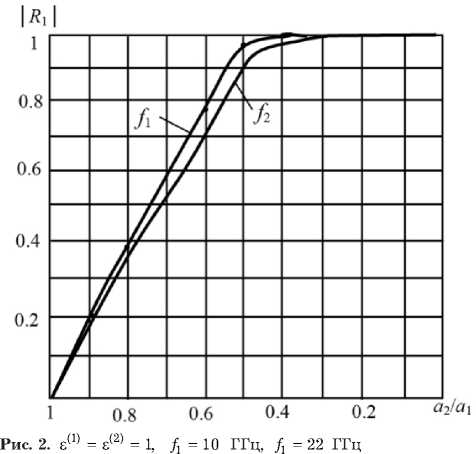
В среде Microwave Studio была смоделирована ступенька в прямоугольном волноводе размерами 23 x 10 мм при разном отношении a 2 / a i . Результаты моделирования приведены на рис. 2–9.

Результаты моделирования показывают, что с увеличением толщины ступеньки поле концентрируется в более широкой области, а коэффициент стоячей волны (КСВ), естественно, возрастает. Для подтверждения адекватности формулы (7) при моделировании были измерены значения КСВ при разных a ₂/ a ₁ на частоте 10 ГГц.

Как видно из рис. 9 расчетная кривая достаточно близко совпадает с кривой, полученной

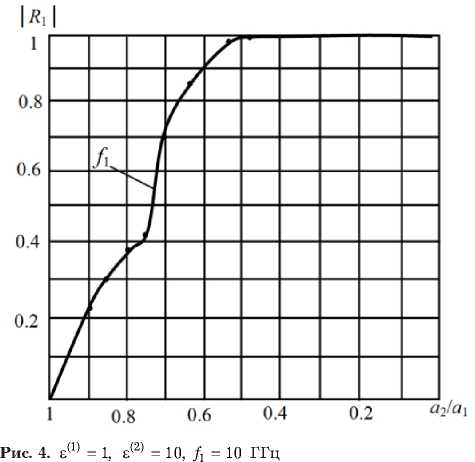
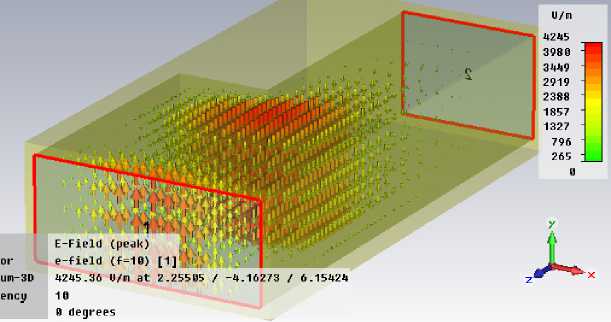
Рис. 5. Модуль поля Е при a ₂/ a ₁ = 0.4

Рис. 6. КСВ структуры при a ₂/ a ₁ = 0.2

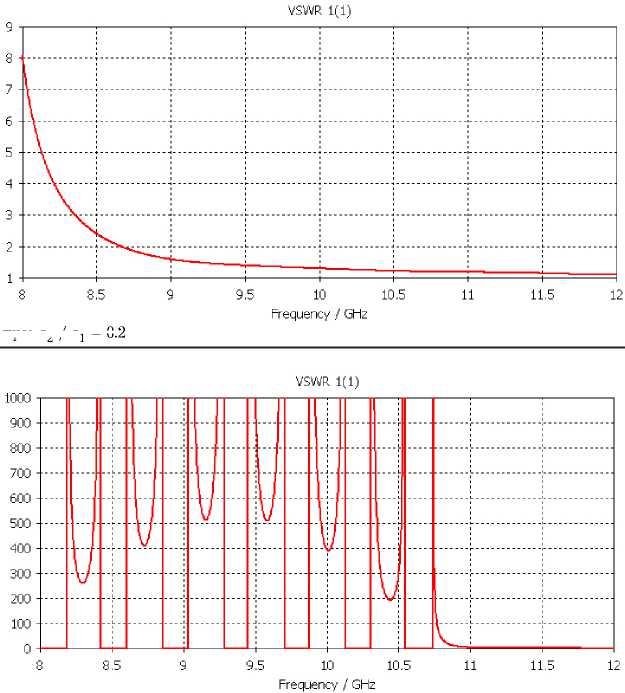
Рис. 7. КСВ структуры при a ₂/ a ₁ = 0.4

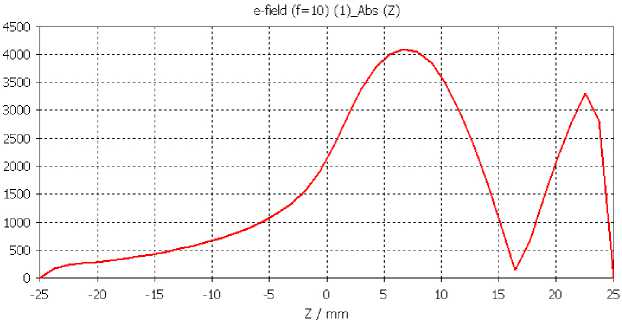
Рис. 8. Модуль поля Е вдоль оси z

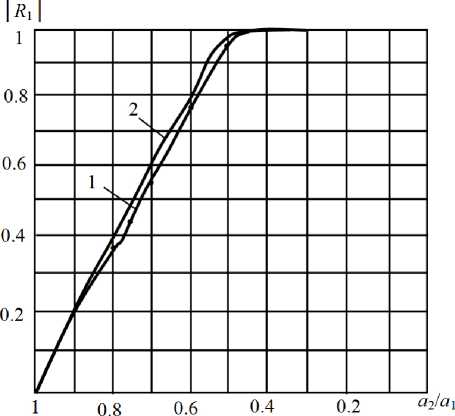
Рис. 9. е ⁽¹⁾ = 1, е ⁽²⁾ = 1, f = 10 ГГц: 1 — расчитанная кривая;

2 – результат моделирования

в результате моделирования, что подтверждает адекватность формулы (7).

Результаты статьи можно использовать при проектировании ступенчатых переходов и при проектировании других неоднородностей в прямоугольном волноводе.

Аналогичным образом может быть рассмотрено и Е-плоскостное ступенчатое сочленение двух прямоугольных волноводов.