Проектирование игольчатого дросселя с применением средств вычислительной гидродинамики

В настоящее время средства вычислительной гидродинамики широко применяются при исследовании, разработке и проектировании гидравлических аппаратов. CFD-моделирование применяется для оптимизации конструкции клапанов с точки зрения отсутствия кавитации [1–4], достижения заданных рабочих характеристик [5–10]. Кроме того, численное моделирование течения жидкости в проточной части гидроаппарата позволяет, например, оценить величину гидродинамической силы, действующей на запорно-регулирующий элемент клапана [11–13], исследовать методы снижения ее величины [14–16], а также получить статические и динамические характеристики гидроаппарата [17–19] на этапе эскизного проекта. При этом, как правило, на начальном этапе проектирования проточная часть аппаратов разрабатывается в соответствии с инженерными методиками расчета и затем совершенствуется посредством изучения гидродинамики потоков.

Данная работа посвящена разработке оптимальной конструкции игольчатого дросселя с точки зрения получения заданной пропускной характеристики и гидродинамической картины течения в проточной части клапана с определением сил, действующих на запорно-регулирующий элемент со стороны потока посредством численного моделирования течения жидкости в проточной части дросселя.

Численное моделирование течения жидкости в проточной части разрабатываемого дросселя позволит подобрать оптимальную конфигурацию проточной части, оценить нагруженность при- вода перемещения запорно-регулирующего элемента, а также проанализировать гидродинамическую картину течения жидкости в проточной части дросселя и при необходимости модифициро- вать конфигурацию иглы и седла.

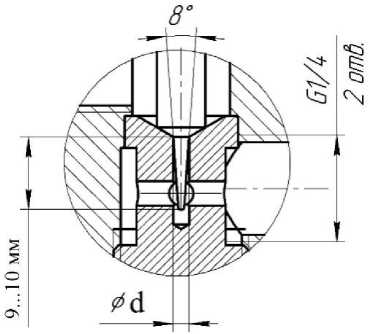
Рис. 1. Элемент проточной части исследуемого дросселя Fig. 1. Element of the flow part of the throttle

Верификация параметров моделирования и проверка адекватности подхода по выбору оптимальной конфигурации проточной части производится путем экспериментального исследования разработанного дросселя с получением его действительной пропускной характеристики.

Объект исследования

Объектом исследования является игольчатый дроссель, основные размеры проточной части показаны на рис. 1. Данный аппарат был разработан в рамках проводимого исследования при следующих исходных параметрах: рабочая жидкость – водный раствор спирта 95 %, давление питания не более p пит = 2 МПа, номинальный расход рабочей среды при перепаде давлений на дросселе Δ p др = 0,1 МПа составляет m = 40 г/с. К характеристикам клапана предъявляются следующие требования: пропускная характеристика линейная, локальные скорости жидкости в рабочем диапазоне расходов не превышают 1,5 м/c.

Материалы и методы

Для предварительного определения диаметра проходного сечения дросселя используется уравнение Торричелли [20, 21]:

Q = m a др

^{2 А} Р др ^ρ

где μ ‒ коэффициент расхода, для игольчатого дросселя составляет 0,75…0,80 [20‒25]; A др ‒ диаметр проходного сечения дросселя (отверстия).

Угол конусности определялся по максимальному ходу запорно-регулирующего элемента согласно рекомендациям [20‒25], который в данном исследовании был задан в диапазоне 9…10 мм, 70 % из которого является рабочим.

Результаты расчета по уравнению (1), а также углы конусности иглы представлены в табл. 1.

Таблица 1

Предварительные размеры игольчатого дросселя

Table 1

Preliminary dimensions of the needle throttle

Исполнение иглы	Диаметр отверстия, мм	Угол конусности, град
01	3	8
02	3,5	8

Таким образом, результаты предварительного расчета параметров дросселя показали, что по заданным характеристикам возможно два исполнения дросселя. Для определения оптимального соотношения геометрических параметров проточной части и, следовательно, рекомендуемого к изготовлению исполнения дросселя необходимо провести сравнительный анализ пропускных характеристик двух исполнений.

Зная диаметр условного прохода и угол конусности иглы, можно рассчитать пропускную ха- рактеристику дросселя, отражающую зависимость расхода через дроссель от хода иглы. Существенной проблемой при расчете такой характеристики для квадратичного дросселя является неопределенность значения коэффициентов местных сопротивлений его проточной части.

Существует две основные методики расчета коэффициента местного сопротивления дросселя. Первая основана на уравнении Торричелли (1) с учетом рекомендаций по величине коэффициента расхода [20‒25]. Вторая методика, описанная в [27], предполагает расчет коэффициента местного сопротивления в зависимости от скорости жидкости итерационным методом. Рассчитанные пропускные характеристики дросселя по этим методикам для каждого из двух исполнений показаны на рис. 2. Как видно, расчетная величина расхода рабочей жидкости через дроссель в каждом положении иглы существенно зависит от выбранной величины гидравлического сопротивления, то есть от выбранной для расчета методики. Поэтому необходимо провести численное моделирование течения жидкости в проточной части дросселя.

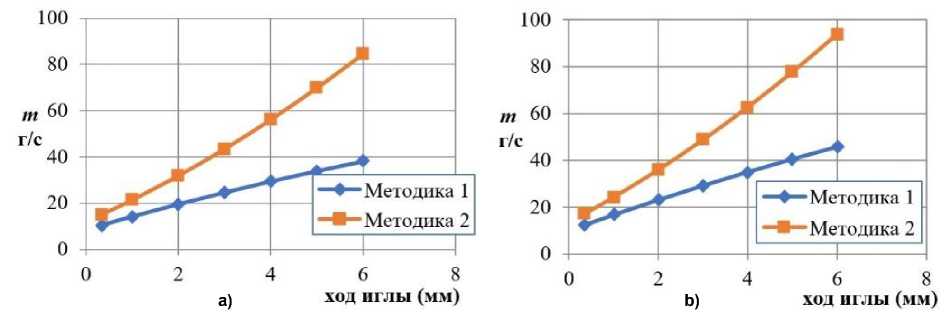
Рис. 2. Расчетные пропускные характеристики дросселя: а) исполнение 01; b) исполнение 02

Fig. 2 Calculated flow characteristics of the throttle: a) version 01; b) version 02

Моделирование течения жидкости в проточной части дросселя выполнено в программном модуле AnsysFluent, позволяющем получить пространственную картину течения воды внутри испытуемой арматуры и определить её интегральные характеристики.

Обработка геометрических моделей выполнялась в программном модуле AnsysDesign Modeler, сеточных моделей – в модуле AnsysMeshing. На основании геометрических моделей дросселя была определена и достроена область течения внутри клапана.

Модель проточной части дросселя выполнена в трехмерном варианте. Изображение модели представлено на рис. 3.

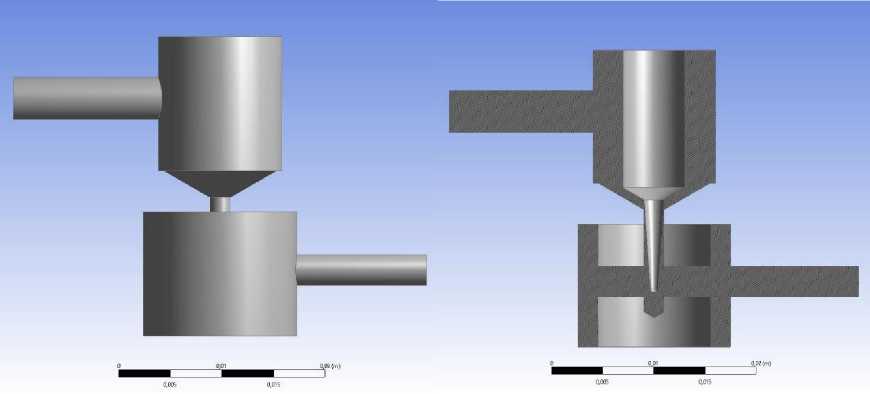
Рис. 3. Элемент проточной части исследуемого дросселя (исполнение 1)

Fig. 3. Element of the flow part of the throttle under study (version 1)

Расчетная область течения была разбита на конечно-объёмную расчётную сетку. Сетка – гибридная, состоит из многоугольников и тетраэдров во внутренних областях течения и 7 призматических слоев в пристеночной области течения. Для создания сетки использовалась расширенная размерная функция элементов – ProximityandCurvature, которая позволяет локально уточнить плотность сетки и задать нужное количество элементов.

Для расчета была использована модель турбулентности k-ε Realizable .

Согласно представленной геометрической модели исследуемого дросселя, была создана конечно-элементная расчетная сетка, представлена на рис. 4. При построении расчетной сетки использовался препроцессор AnsysMeshing.

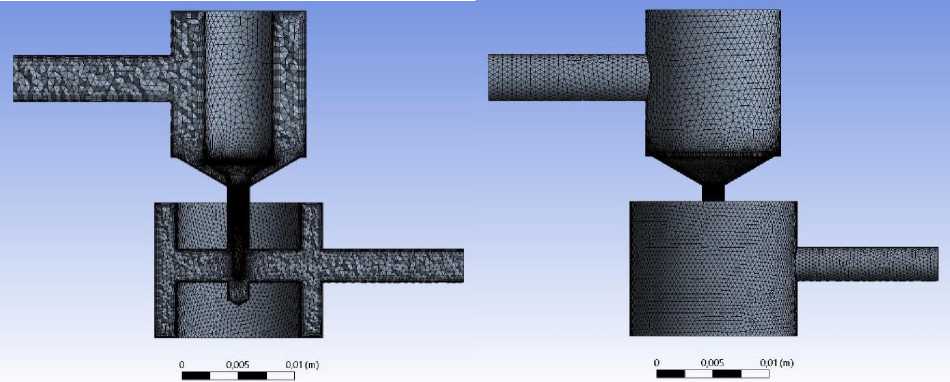
a)                                                                b)

Рис. 4. Расчетная сетка конечно-элементной модели (исполнение 1)

Fig. 4. Mesh of the finite element model (version 1)

В качестве рабочей среды принята жидкость – спирт этиловый 95 %. Значения основных свойств рабочей среды указаны в табл. 2.

Граничные условия для исследуемых случаев приведены в табл. 3.

Таблица 2

Таблица 3

Свойства рабочей среды

Table 2

Properties of the working fluid

Наименование параметра	Значение
Плотность, ρ	790 кг/м3
Коэффициент динамической вязкости, μ	0,0012∙кг/м∙с

Граничные условия

Table 3

Boundary conditions

Локация	Значения параметров
Вход в дроссель, Inlet	p = 100000 Па
Выход из дросселя, Outlet	p = 0Па
На стенке трубы, Wall	u = 0 м/с стенки гидравлически гладкие

Расчет проводился в стационарной постановке (Steady-State). При расчётах использовалась расширенная пристеночная функция (EnhancedWallTreatment), позволяющая с высокой точностью определить характер течения вблизи стенки, моделировать потоки с интенсивным перемешиванием и резкими локальными изменениями скорости. Алгоритм решения связки уравнения движения и неразрывности (Pressure VelocityCoupling) при решении выбирался SIMPLEC. Для получения точных решений использовалась дискретизация второго порядка точности (SecondOrderUpwind). Окончание расчета происходило при достижении решения уравнений импульса и неразрывности погрешностей 10–6.

Результаты и обсуждения

Результаты расчета массового расхода через дроссель представлены в табл. 4.

По данным из табл. 4 видно, что величина силы, действующей на запорно-регулирующий элемент дросселя, не превышает 6 Н и, таким образом, можно сделать вывод о ненагруженности привода запорно-регулирующего элемента.

Таблица 4

Результаты численного моделирования

Table 4

Results of numerical simulation

Исполнение дросселя	Ход иглы дросселя, мм	Массовый расход жидкости, г/с	Сила, действующая на ЗРЭ от стороны потока, Н
01	1	8,2	4,85
	4	24,6	2,13
	7	35,8	0,98
02	1	9,5	5,89
	3	22,9	3,39
	6	41,1	1,74

На рис. 5 показаны кривые пропускных характеристик дросселя в исполнения 01 и 02, полученных путем численного моделирования в AnsysFluent, а также линии тренда, построенные по линейному закону с указанием величины достоверности аппроксимации.

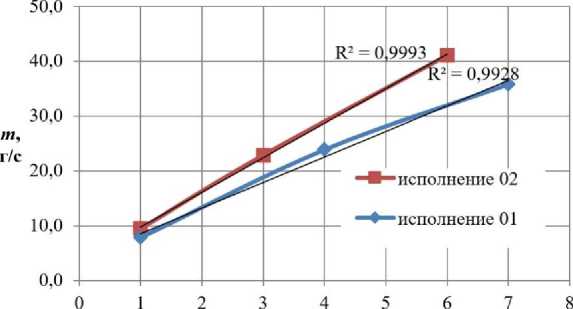
ход иглы, мм

Рис. 5. Сопоставление пропускных характеристик, полученных по аналитическим методикам и по результатам численного моделирования

Fig. 5. Comparison of flow characteristics obtained using analytical methods and the results of numerical simulation

Анализ кривых на рис. 5 показывает, что наиболее перспективными является конструкция дросселя в исполнении 02 ввиду наибольшей линейности характеристик и полного охвата диапазона регулирования по расходу.

Сравнение кривых на рис. 2 и 5 показывает, что пропускная характеристика, рассчитанная по методике 1, то есть по уравнению Торричелли (1) с учетом рекомендованных в [20‒26] величин коэффициента расхода, показывает удовлетворительную сходимость с кривой пропускной характеристики, полученной в результате численного моделирования потока через дроссель. При этом кривая пропускной характеристики, полученная аналитическим расчетом по методике 2 [27], сущест- венно отличается от кривой, полученной в результате численного моделирования.

Распределения давления и скорости в продольных сечениях дросселя изображены на рис. 6, 7. Как видно из рис. 6, давление жидкости проточной части во всех случаях превышает величину давления насыщенных паров спирта при заданных температурах, следовательно, возникновение очагов кавитации в местах локальных ускорений и разряжений исключается. Кроме того, из рис. 7 видно, что скорости во всех точках проточной части не превышают 1,5 м/с, что соответствует рекомендациям по проектированию гидравлической аппаратуры такого типа.

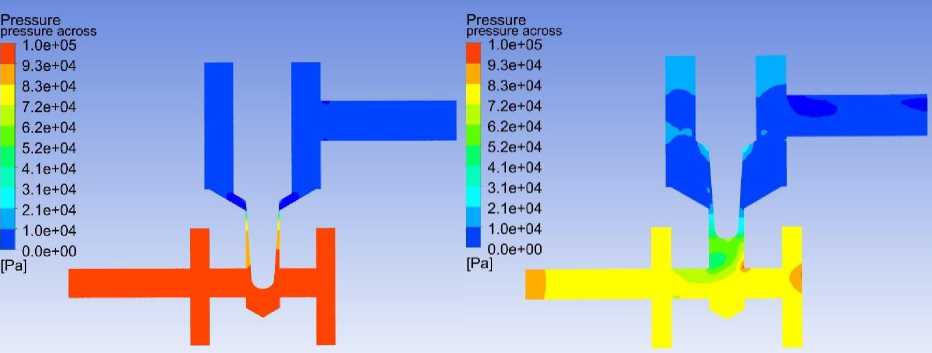
а)

b)

Рис. 6. Распределение давления в продольном сечении дросселя исполнения 02: а) перемещение иглы 1 мм; b) перемещение иглы 6 мм

Velocity velocity along 1

1.5e+01

1.3e+01

1.2e+01

1.0e+01

8.8e+00

7.3e+00

5.9e+00

4.4e+00

2.9e+00

■ 1.5e+00

• ¹    O.Oe+OO

[m sA-1]

Fig. 6. Pressure distribution in the longitudinal section of the throttle of version 02: a) needle movement 1 mm; b) needle movement 6 mm

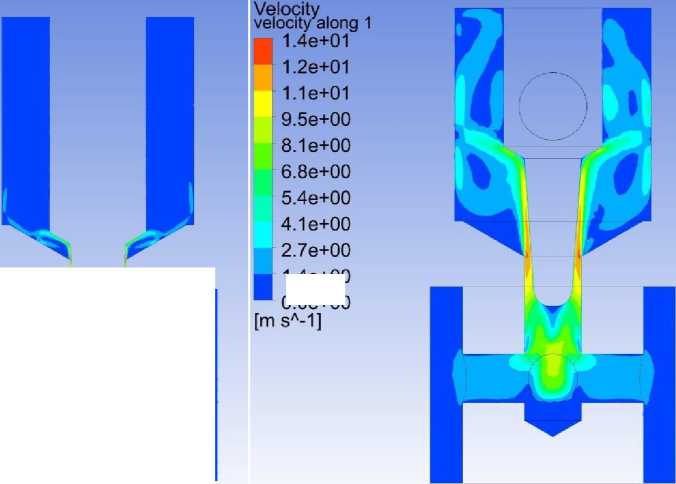
b)

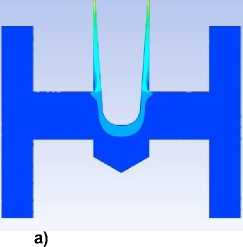
Рис. 7. Распределение скорости в продольном сечении дросселя исполнения 02: а) перемещение иглы 1 мм; b) перемещение иглы 6 мм

1.4e+00

O.Oe+OO

Fig. 7. Velocity distribution in the longitudinal section of the throttle of version 02: a) needle movement 1 mm; b) needle movement 6 mm

Спроектированный игольчатый дроссель в исполнении 02 был изготовлен и подвергнут гидравлическим испытаниям по методике, разработанной согласно ГОСТ 33257-2015, в результате которых получена действительная пропускная характеристика дросселя. На рис. 8 приведено сопоставление пропускных характеристик дросселя, полученных в результате численного моделирования и гидравлического испытания, в пределах относительной погрешности 5 %. Кроме того, на рис. 8 показана линейная аппроксимация экспериментальных данных с указанием величины достоверности аппроксимации, которая составляет R = 0,9989.

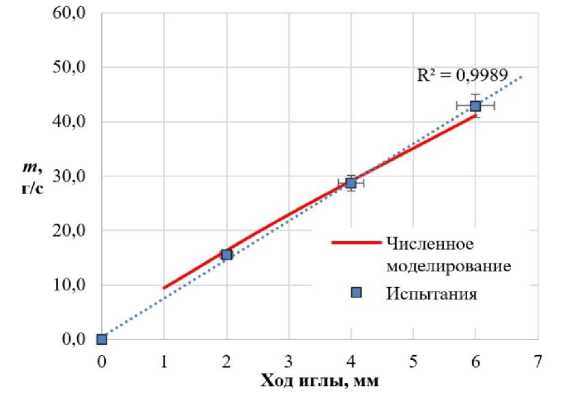
Рис. 8. Сопоставление пропускных характеристик, полученных в результате численного моделирования и экспериментальных исследований

Fig. 8. Comparison of flow characteristics obtained as a result of numerical modeling and experimental studies simulation

Как видно из рис. 8, расчетная и действительная пропускные характеристики показывают удовлетворительную сходимость. Кроме того, по линейной линии тренда, построенной по результатам испытаний, видно, что пропускная характеристика является линейной с высокой достоверностью аппроксимации в пределах рабочего диапазона хода иглы.

Исходя из полученных результатов, можно сделать следующие выводы:

• 1.    Расчет пропускной характеристики квадратичного дросселя по уравнению Торричелли (1) с учетом рекомендаций [20–25] по выбору величины коэффициента расхода показывает удовлетворительную сходимость с результатами численного моделирования.

• 2.    Применение средств вычислительной гидродинамики позволяет рассчитать величину гидродинамической силы, оценить гидродинамическую картину течения жидкости в проточной части, а также выбрать оптимальные с точки зрения заданной пропускной характеристики геометрические параметры элементов проточной части дросселя.

• 3.    Выбранные параметры моделирования течения жидкости в проточной части игольчатого дросселя позволяют рассчитать гидродинамику течения с удовлетворительной точностью, что подтверждается экспериментальными исследованиями пропускной характеристики дросселя.