Проектирование металлической индуктивной диафрагмы

• 1    Расчет параметров индуктивной диафрагмы

  • 1.1    Вывод формулы для коэффициента отражения

Металлические диафрагмы широко используются для создания волноводных фильтров, ответвителей, резонаторов и аттенюаторов.

Диафрагма представляет из себя поперечную перегородку в волноводе, устанавливаемую перпендикулярно силовым линиям электрического поля или вдоль них и создающая соответственно емкостную или индуктивную проводимость для ослабления волн определённого типа.

Для решения задачи дифракции основной волны прямоугольного волновода на диафрагмах, расположенных на стыке двух диэлектриков с различными диэлектрическими проницаемостями применяется метод частичного обращения оператора. Аналитическое решение полученных интегральных уравнений в первом приближении даёт возможность получить простые формулы для коэффициентов отражения и прохождения через емкостную диафрагму как основной волны, так и возникающих вследствие дифракции высших типов волн.

Нужно отметить практическую значимость полученных в статье результатов, так как при использовании диафрагм (емкостной, индуктивной) в качестве крепёжных элементов, например для p-i-n диодов и других активных приборов, необходимо знать, какую часть энергии неоднородность отразит, а какую пропустит. Возможно также использовать полученные аналитические выражения в системах автоматизированного проектирования устройств СВЧ и КВЧ диапазонов.

Рассмотрим дифракцию основной волны единичной амплитуды на емкостной диафрагме, сечение которой в плоскости неоднородности показано на рисунке 1.1а. На рис. 1.1б показано сечение в направлении переноса электромагнитной энергии. Щель в волноводе имеет ширину

A w = w₂

— w 1 , координату центра щели обозначим y₀ =

Wj + w₂

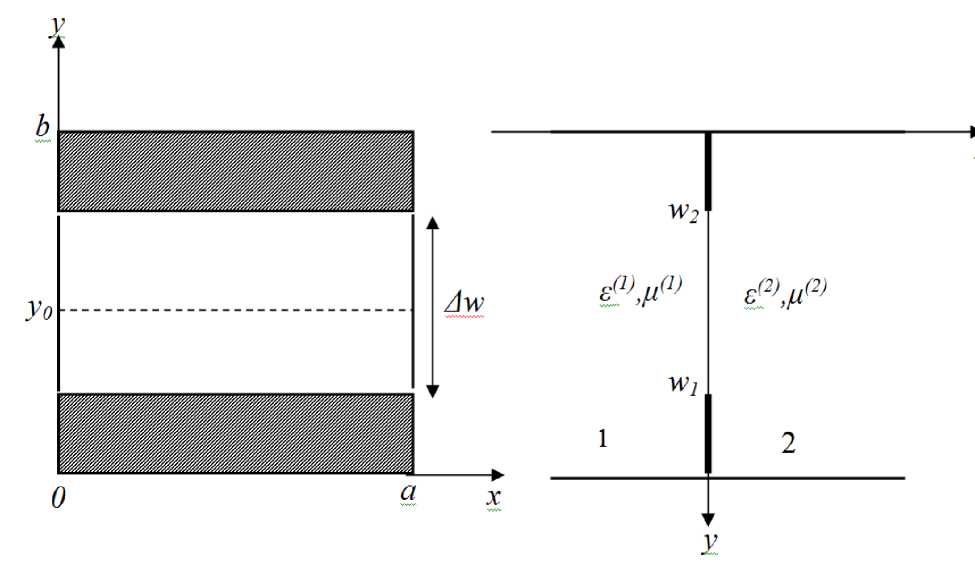
Рис. 1.1 - Емкостная диафрагма в прямоугольном волноводе

Будем считать, что падающая волна, распространяющаяся в линии передачи с идеально проводящими и бесконечно тонкими стенками, набегает из точки с координатой z = —^ , и волновод согласован при z = +^ .

Поле падающей волны возбуждает в первой среде ( z <  0 ) отраженные типы собственных волн, а во второй ( z > 0 ) проходящие волны основного и

высших типов. Поэтому электрическое поле в линии передачи, её поперечные составляющие, можно представить в виде гармоник /2, 10/.

Пусть падает волна H 10 ( n =1, m =0):

где

E y

-1) (1'z         *h(I)z                 <1)z

e 0 z + Re 0 z + ^ Rnern z n=1

E y

Te -^’z + £ t/-” n=1

z

cos

cos

h(0 =, k^s*"'^”

^-

К

^ nny ^

V b )_

^ nny ^

V b )_

2n nv

• (roc sin — ,

V a )

. ( nx ) sin —

V a )

,

(i)

n

nn

11 ь)

^-

ky i ^ i

i = 1,2 ;

, to ko =- c

- волновое число в вакууме.

При больших n можно считать

Г

nn

~

b

На основе уравнений Максвелла [1,2,3] можно записать:

d H z	д H y	= ik s Ex ,	д Ez	д E y	= ik P H x ,
д у	д z		д y	д z
д Hx	д H z	= iks:Ey,	д Ex	д Ez	= ik ^ Hy ,
д z	д x		д z	д x
д H y д z	_ дH z b y	= ik s Ez ,	д E y д z	_ дE z b y	= ik p Hz.

Откуда можно получить (1.1), используя приближение п Т дx2    ( a )

д H _{x =} h () _F

(1.1)

дz      ify(l) y

Используя

формулу(1.1),

можно

записать

выражение

для

составляющей магнитного поля:

H⁽x ) =

_{h 0} ( 1 ) 2

i kp? ¹ )

-< ) ⁽ e

,^{- ih} o ^{1 ) z}

—

to

Re h ^z _{) +} £ n = 1

R        ( 1 )

n-en z

cos

пп y

(1.2)

n

_Hx (2)

(2) ²

T

i ku2'

^-

i0

- ih '²^ e ⁰

^

-z n=1

T

n

n

r'2)z    ( плу )

e n cos I ——

ь ) •

Запишем граничные условия (ГУ) при z = 0 , у е [ w_Pw₂ ] ,

Е(У = E(2) = E(y),

Откуда получим:

w2

1 + R = T = -1 Е(у' )dy'

w1

,

(1.3)

w2

Ru = Тп =^( Е(У' )cos w1

f £) dy -.

Выражения (1.3) получили, предполагая, что ( 1 + R) суть свободный

член, а R_n - остальные коэффициенты разложения Фурье.

Используем ГУ для Н^ , определённые системой (1.2), Н⁽¹⁾ = Н⁽²⁾ при z = 0 , у g [ w_pw₂ ] , получим:

_{h 0} ( 1 )

ц ¹ )

(1 - R) -

( 1 ) 0

_{h 0} ( 2 )

ц ² )

Ц _{ih 0} ( 2 ) ц ^2ь

у1 R

£ ""Fc)cos п=1 Г п

п п у

V Tn    ( ппу

X W 2 ) cos I , п = 1 ¹ п        V b

(1.4)

.

Учитывая, что T = 1 + R , перенося T из правой части в левую в уравнении (1.4) и перегруппировав члены уравнения, можно записать:

h ( ¹ )                ( ² )               ^ч

-Уу ( 1 - R) - -Уу ( 1 + R) = i £ ц            ц              п = 1

( hr

V ^ц

+

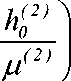
( h>

V ^ц

^“

h> J

ц 7

_{h 0} ( 1 ) 2            _{h 0} ( 2 ) 2

ц ⁽ 1 Г )   ц ^{( 2 )}_Г(_г

^

= - i X п=1

_h0 (1)²

ЦПрО)

+

Введя дополнительные обозначения, а именно:

ho =

(1)       (2)

Ц ¹ Ц ²

;

Ап =

Ah o

(1)       (2)

00 ---. ц ¹ ц^{2 2} ;

R _n cos

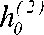
Ц2)г;(2

п п у

Rn cos

(1.5)

пуу b

2 h 0

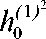
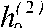
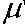
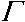
n

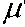
n

представим (1.5) в более компактной форме или

2(Rh„ - Ah) ho (1 + R)

2(Rh - Ah J h ₀

= — 4 i T ^A n^Rn co ^S

nny

^w 2                      x ^w 2

J E(y' )dy ' = -8^ J Е(У' A w1                         n=1 W1

cos

f nny )

I cos

I b )

| b)

dy ’.

• 1.2    Метод ортогонализирующей подстановки

Введём следующие обозначения переменных [2,3]:

п   п

Ф =—, ^ = —, bb и представим:

а ( 1 + А )         n A

A n =       — , где 5 n =   - - 1.

n             а nn

Так как Г„--при n ^ x, то можно записать: nb lim 8 A = lim 8'

2 h 0

а

^, n

(1.7)

где

4 b  h⁽ )     h ( 2^2

n h ^ ¹ )   ^ ² )

Введём нормированную реактивную проводимость B в сечении волновода при z = 0 по формуле:

2 (Rh ₀ - A h ₀ ) h o ( 1 + R)

(1.8)

Учитывая предыдущие обозначения и формулы (1.7) и (1.8), уравнение (1.6) можно записать в виде

В\Е(ф)dф = ]Г\Е(ф.)■ cos(n®)cos(nф)( 1 + 5-)1ф ,      (1.9)

а                n = 1                    n

nw,    nw7

.

где ф и 0 изменяются в пределах от -д- до —

Полученное соотношение (1.9) есть не что иное, как интегральное уравнение. По методу Швингера решение таких уравнений основано на введении новых переменных и и v , которые изменяются от 0 до п . Для данного частного случая [2,4]

cos(0) = c + scos(u) ; СО8(ф) = С + SCOs(v), (1.10)

где c = cos

( лу^

v ^b

)

cos

(A )

V 2b )

;

s = sin

( пу^ v ^b

)

sin

V

( nAw

2b

)

Далее воспользуемся соотношением

cos(n 0 )cos(n ф ) _  1^ yi cos(nu)cos(nv)

n              2       n=1

Тогда уравнение (1.9) запишется в виде:

- j E(V)d^dv = a Jodv

-1 ins + ^ cos(nu)cos(nv) + у 5 cos(nu)cos(nv) 2        n=1           n             n=1

= j Е( Ф )Т dv

(1.11)

dv.

1.3 Квазистатическое приближение

Рассмотрим первое приближение

5 _п = 0, n >  0 .

Приравнивая коэффициенты при cos(nu) , уравнение (1.11) распадается

на два:	B 1 — = - ins a   2
и	J Е( ф ) <^cos(nv)dv = 0,n >  0 .               (1.12) 0       dv

Равенство (1.12) выполняется только тогда, когда

E( v )d P = C o , dv

где C = const .

С помощью математических преобразований из (1.10) находим v

, cos( ф ) - c.    dv         sin( m )

v = arccos(----) ^ — = s       dm  J14 c- cos(ф) Y

\ V s J

Тогда Е( ф ) записывается в следующем виде:

Е(ф) =

C_ossin( ф )

s² - (c — cos( ф ))²

(1.13)

Для определения Co из (1.13) воспользуемся выражением (1.3), из которого следует, что:

С = 1 + R .

Рассмотрим частный случай, когда волновод полый (наиболее часто используется на практике)

/ ¹ ) = / ² ) = 1,

^ ¹ ) = А ⁽ 2 ) = 1,

а =

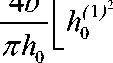
^п 0     1

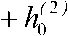
h

(1) 0

0 ^—

( П )

V a J

h = 2 h₀ ^{( 1} ) = 2 k₀²

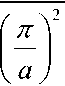
4 b а = — h ₀ ,

П так как

12 b

(1.14)

B = -а • —lns =-- h₀^ns .

2       п

Учитывая, что длина волны в волноводе:

A =

2 п

_h (1)₀

2 п

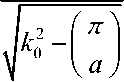
равенство (1.14) можно записать в виде:

B = - —1ns .

A

Но учитывая равенство (1.8) и то, что для воздушного волновода

A h₀ = 0 , получаем:

R = - ^B-, 2 + iB а используя равенство (1.3)

T =  ²

2 + iB

.

В общем случае, когда диафрагма находится на стыке двух

диэлектриков с разными значениями диэлектрических и магнитных проницаемостей, исходя из того, что а( 1 + 5п)       и\   1

^A n                 , ° n            ¹ ’

n

а

и обозначая

(1)2

2    h0

H   ^ 1

(2)2

^2),

коэффициенты отражения и прохождения находятся так:

inAh0 - bH2lns

R =---------------2------ ,

inh0 + bHolns

т = in(h0 + Ah0) inh0 + bH2 Ins '

Коэффициент стоячей волны находится по формуле:

К = l+Rсд 1 -|R|.

• 1.4    Расчёт параметров в первом приближении

Расчет по выведенным выше формулам проводился в системе MathCad.

Составляющие электрического поля в зависимости от φ , рассчитанного по формуле (1.13) при частоте 10 ГГц, показаны на рис. 1.2-1.4.

На рис. 1.2 показана действительная составляющая электрического поля.

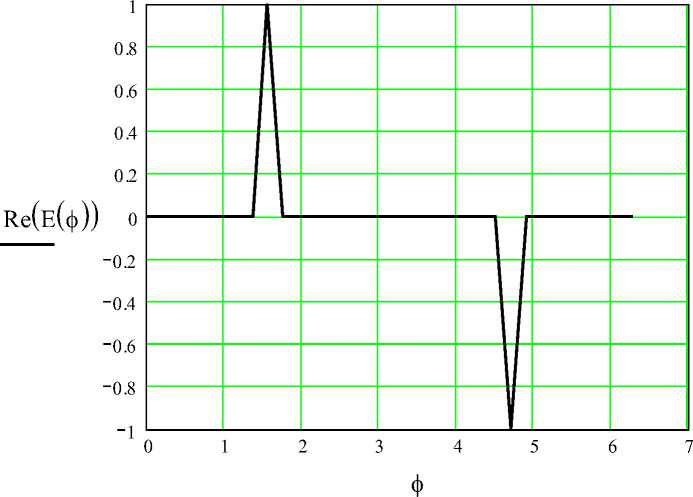
Рис.1.2 –Действительная составляющая электрического поля Е φ

На рис. 1.3 показана мнимая составляющая электрического поля.

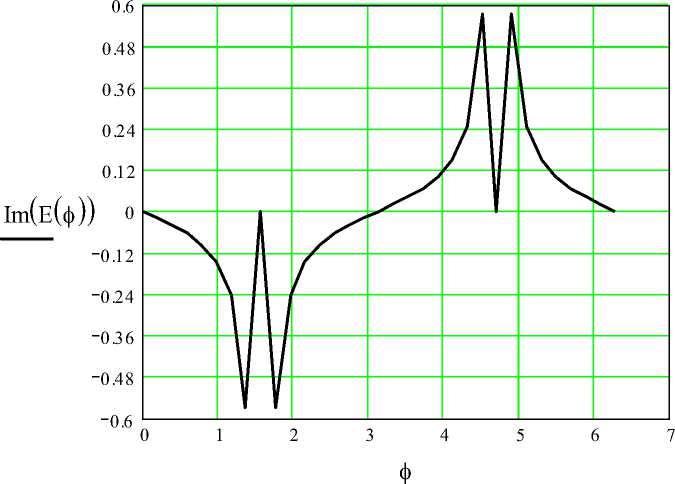
Рис. 1.3–Мнимая составляющая электрического поля Е_φ

На рис. 1.4 показан модуль электрического поля.

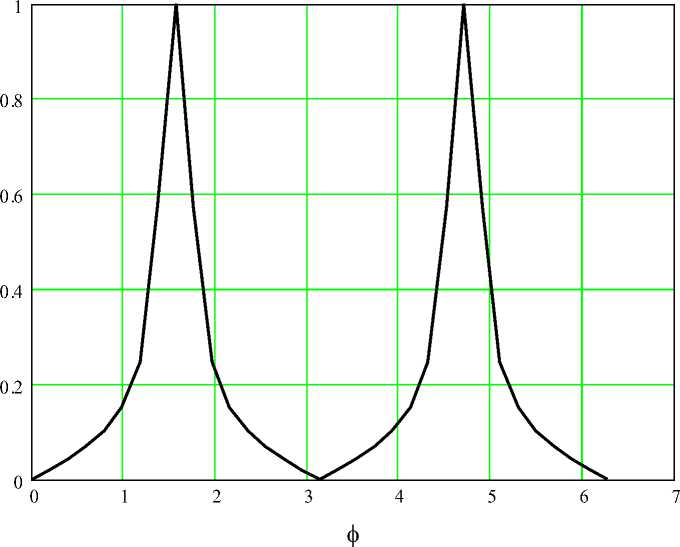
Рис. 1.4 – Модуль электрического поля

Зависимость удельной проводимости B от толщины зазора Δ w показана на рис. 1.5.

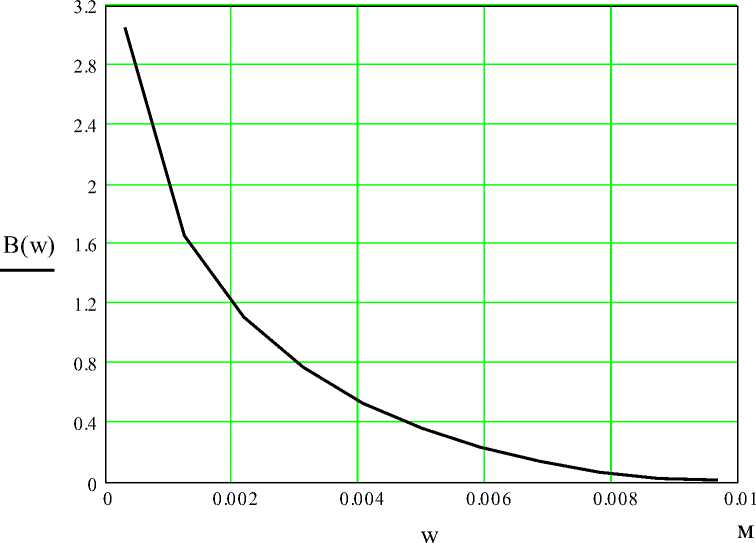
Рис.1.5 – Зависимость В от Δ w

Графики зависимости коэффициента отражения R от ширины зазора w показаны на рис. 1.6-1.8.

На рис. 1.6 показана действительная составляющая коэффициента отражения.

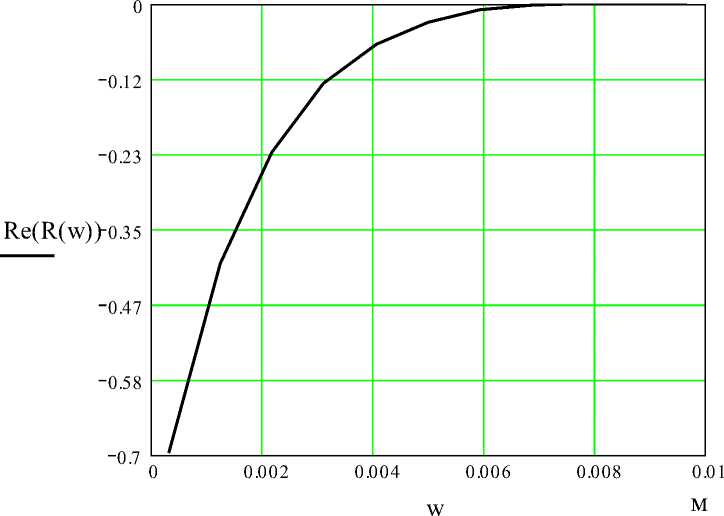
Рис. 1.6 – Зависимость действительной составляющей коэффициента отражения R от ширины зазора Δw

На рис. 1.7 показана мнимая составляющая коэффициента отражения.

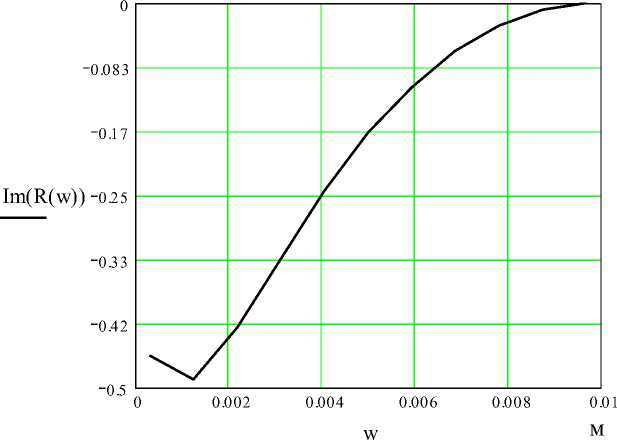
Рис. 1.7 – Зависимость мнимой составляющей коэффициента отражения R от ширины зазора Δw

На рис. 1.8 показан модуль коэффициента отражения.

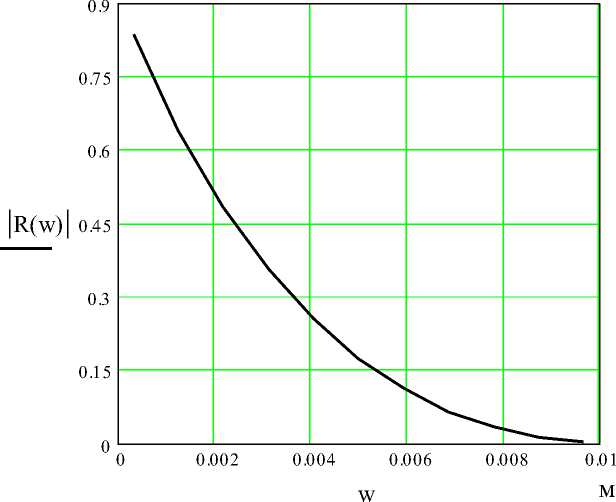
Рис. 1.8 – Модуль коэффициента отражения R от ширины зазора Δw

Коэффициент стоячей волны находится по формуле:

КСВ =

(1 +1 Д р

(1 -1 Д р'

График зависимости КСВ от ширины зазора показан на рис. 1.9.

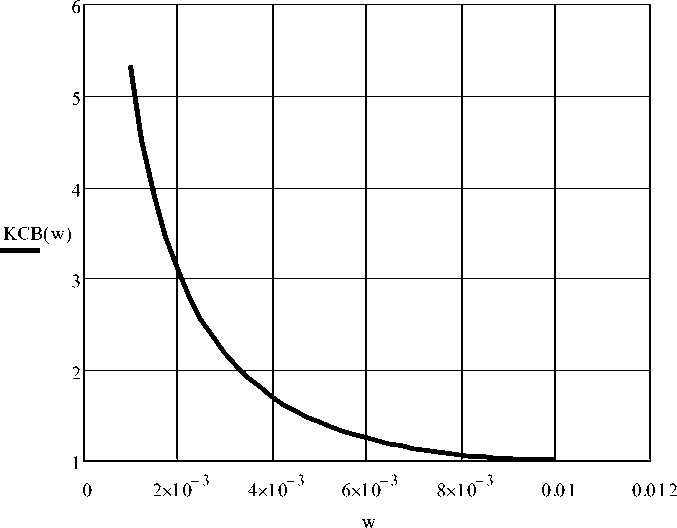
Рис. 1.9 – График зависимости КСВ от ширины зазора Δw (мм)

График зависимости КСВ от частоты показан на рис. 1.10 при J w = —.

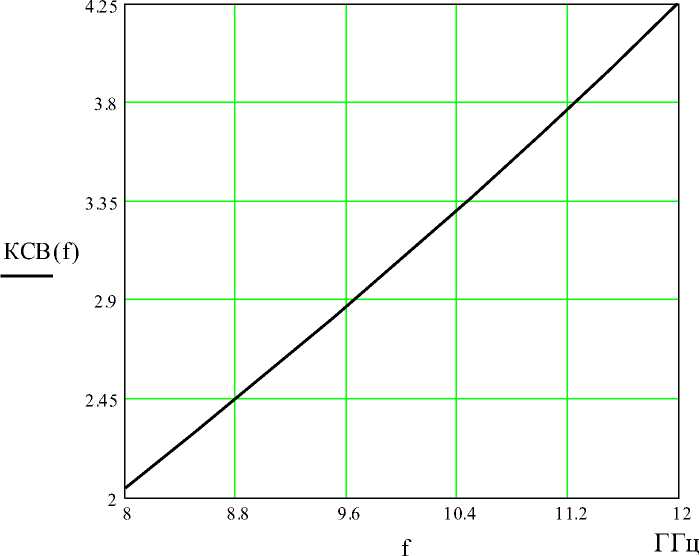
Рис. 1.10 - Зависимость КСВ от частоты (ГГц) при J w = —

• 1.5    Экспериментальные исследования

Коэффициент стоячей волны в зависимости от ширины зазора и частоты измеряется на панорамном измерителе Р2-61 по схеме, представленной на рис.1.11, в котором введены следующие обозначения:

• -     генератор качающейся частоты (1);

• -     индикатор (2);

• -     измеряемое устройство (емкостная диаграмма) (3).

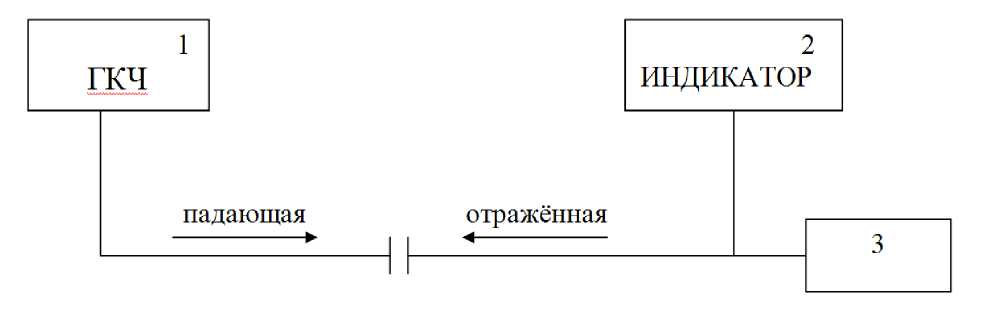
Рис.1.11 – Схема экспериментальной установки

В табл. 1.1 и 1.2 внесены результаты экспериментов.

Табл.1.1

Ширина зазора w	0.6 мм	1.3 мм	2.5 мм	5 мм	7.5 мм	10 мм
КСВ	11.2	4.3	2.5	1.4	1.15	1.01
Табл. 1.2

Частота f , ГГц	8	8.5	9	9.5	10	10.5	11	11.5	12
КСВ	2	2.3	2.6	2.86	3.15	3.4	3.7	3.97	4.25

По экспериментальным данным построим графики зависимости КСВ от ширины зазора и частоты.

Полученные экспериментальные кривые показаны на рис. 1.12 и 1.13.

На рис. 1.12 показана зависимость КСВ от ширины зазора Δ w .

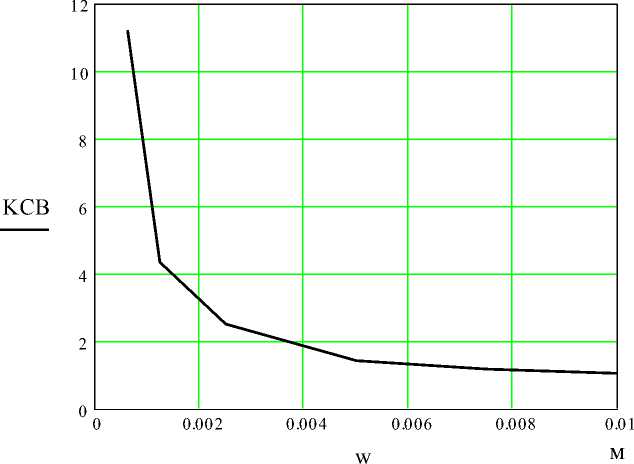
Рис.1.12 – Зависимость КСВ от ширины зазора Δ w (м)

На рис. 1.13 показана зависимость КСВ от частоты при ширине зазора

b

Δ w =

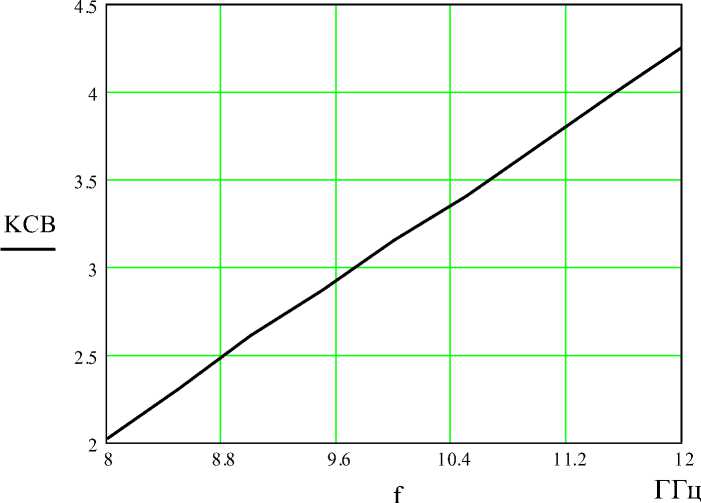
Рис. 1.13 – Зависимость КСВ от частоты при ширине зазора

b

Δ w =

Ниже приведены сравнительные характеристики расчетных и экспериментальных кривых.

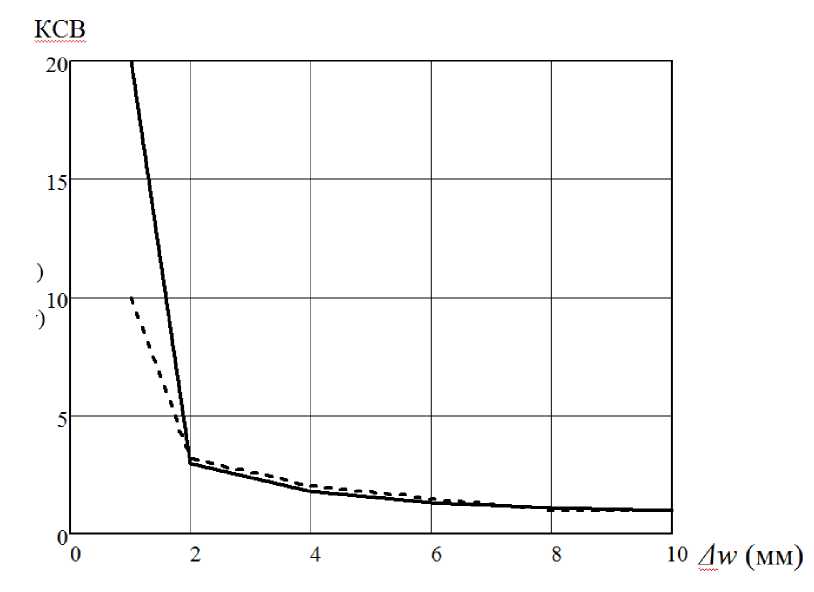
Рис. 1.14 – Зависимость КСВ от ширины зазора: сплошная -

теоретическая кривая; штриховая - экспериментальная

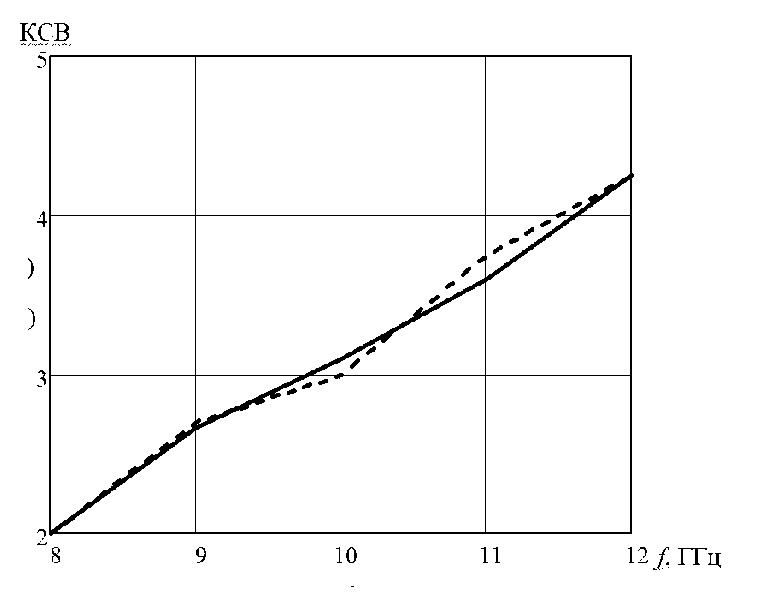
Рис.1.15 – Зависимость КСВ от частоты : сплошная -теоретическая

кривая; штриховая - экспериментальная

Как видно из рис. (1.14)и (1.15) экспериментальные и расчетные характеристики хорошо совпадают.

2 Проектирование емкостной диафрагмы в среде CST Microwave

Studio

Проведем моделирование рассчитанных диафрагм [5], для этого войдем в программу CST Microwave Studio. Смоделированная емкостная диафрагма показана на рис. 2.1.

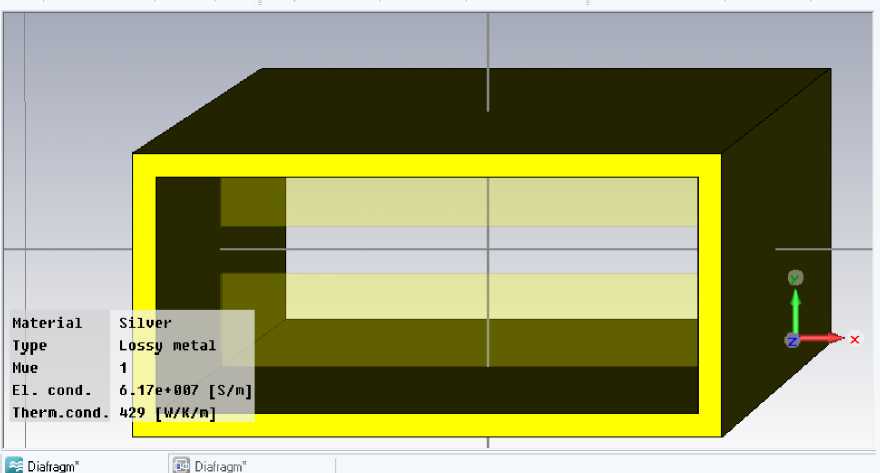
Рис. 2.1 - Волновод 23×10 мм из серебра с емкостными диафрагмами

Результаты проектирования металлической емкостной диафрагмы в прямоугольном волноводе приведены ниже.

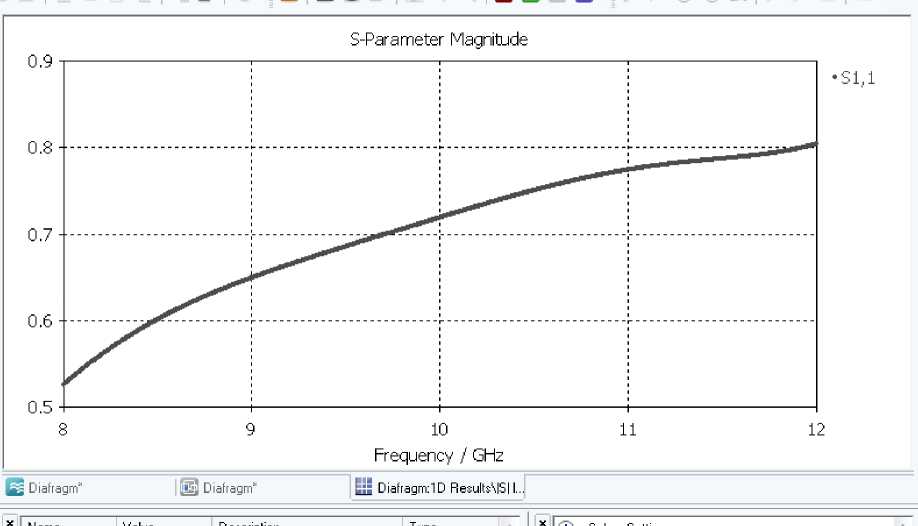
Рис. 2.2 – Зависимость элемента матрицы рассеяния S 11 от частоты для

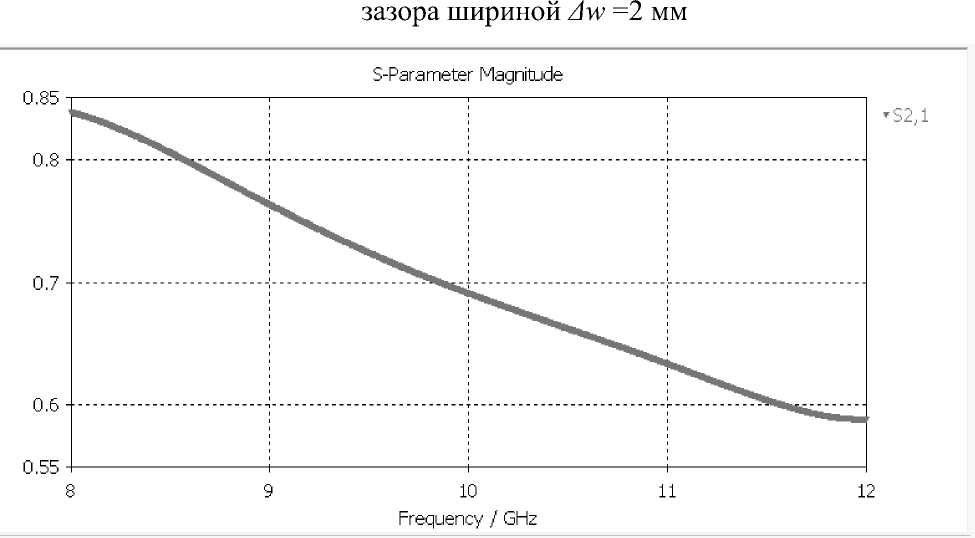
Рис. 2.3 – Зависимость элемента матрицы рассеяния S₂₁ от частоты для

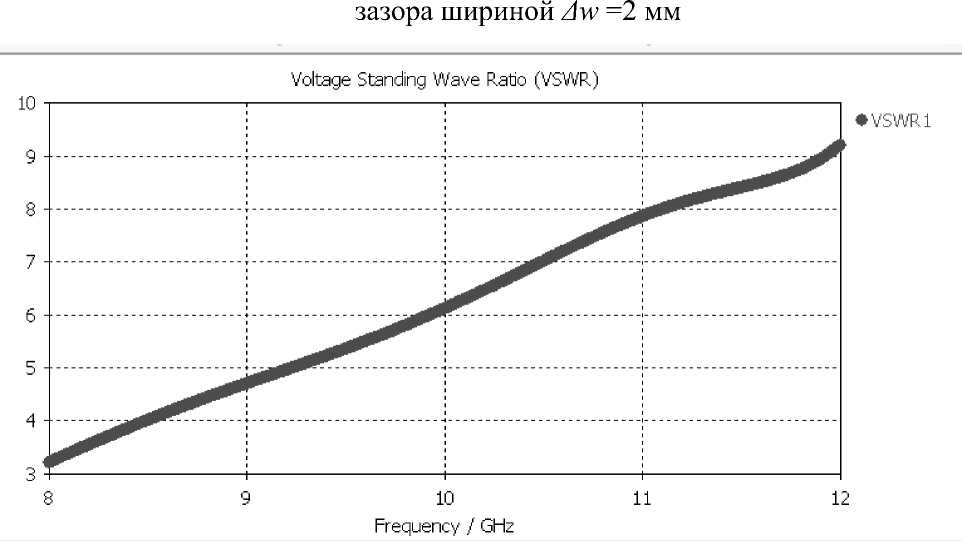
Рис. 2.4 – Зависимость КСВ от частоты для зазора шириной Δw =2 мм

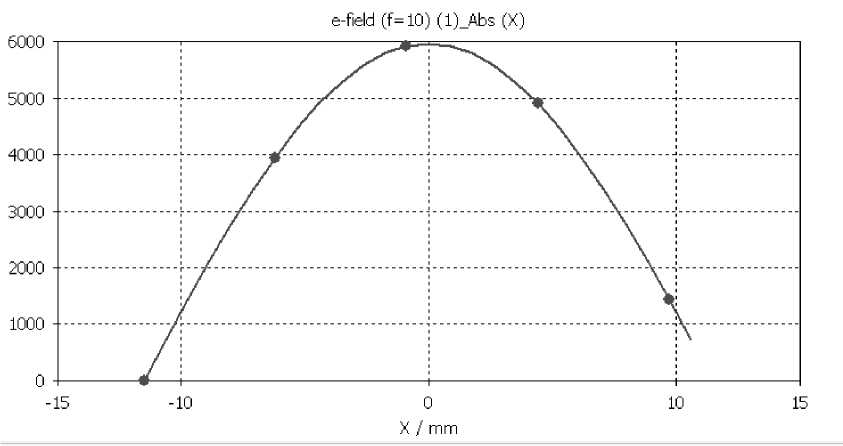
Рис. 2.5 – Модуль составляющей э/м поля Е по x координате для зазора

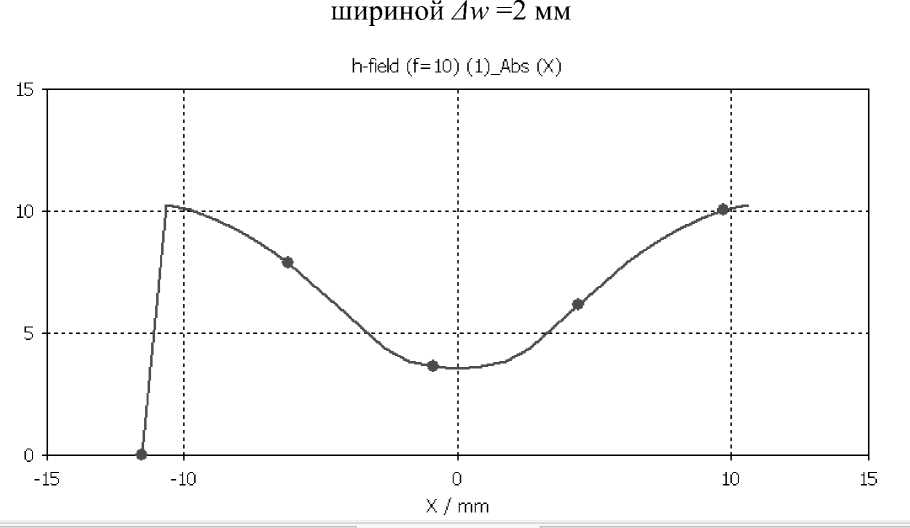
Рис. 2.6 – Модуль составляющей э/м поля Н по x координате для зазора

шириной Δw =2 мм

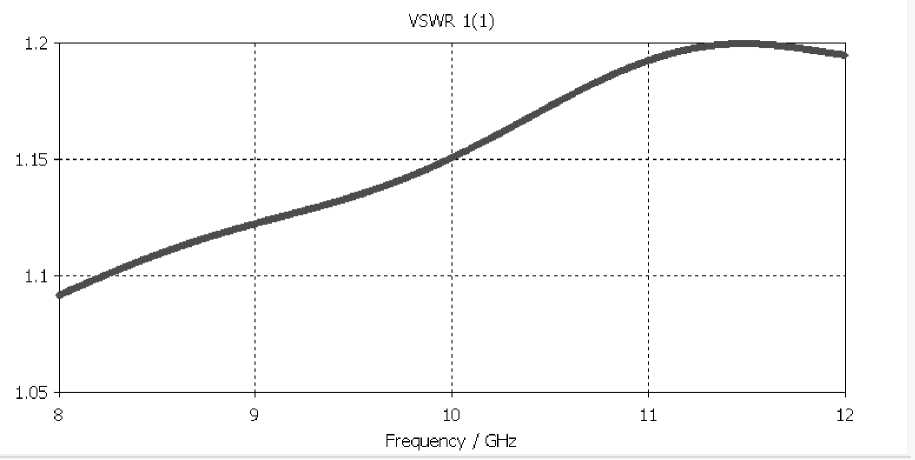
Рис. 2.7 – Зависимость КСВ от частоты для зазора шириной Δw =8 мм

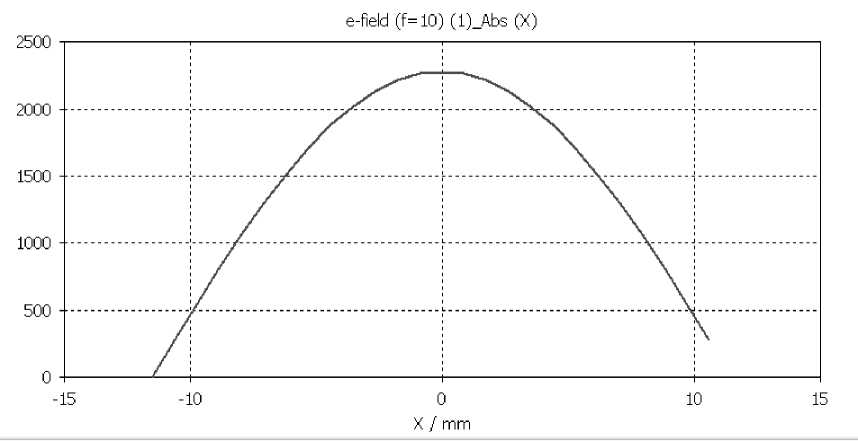
Рис. 2.8 – Модуль составляющей э/м поля Е по x координате для зазора

шириной Δw =8 мм

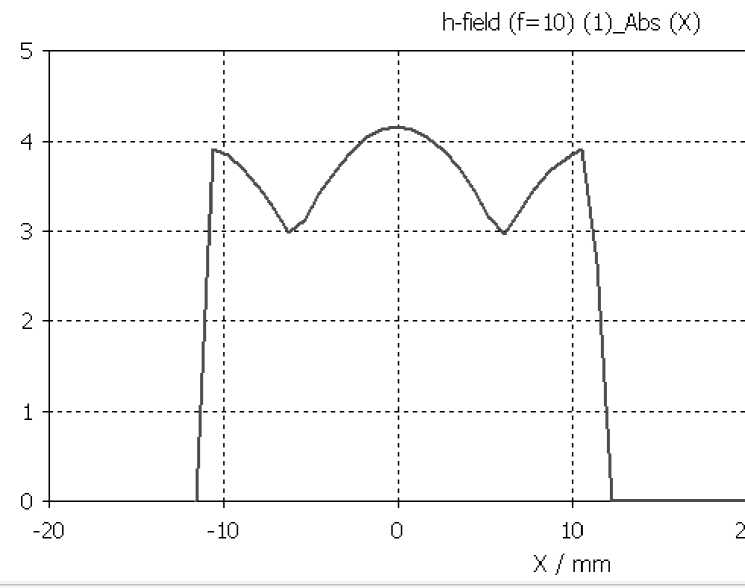
Рис. 2.9 – Модуль составляющей э/м поля Н по x координате для зазора шириной Δw =8 мм

Результаты , полученные в статье позволяют проектировать волноводные фильтры на диафрагмах и волноводные ответвители.