Проектирование широкополосных ферритовых Y-циркуляторов на сосредоточенных элементах

Возможности совершенствования технических характеристик невзаимных ферритовых СВЧ-устройств с Y-сочленением в виде переплетенных индуктивных рамок посредством поиска новых схемных решений ограничены, поскольку любые изменения схемы циркуляторов и вентилей этого типа сводятся к введению дополнительных реактивных элементов либо между общей точкой индуктивных рамок и корпусом, либо в каждое из трех плеч. Таким образом, создание новых невзаимных ферритовых устройств с улучшенными характеристиками сводится к выбору оптимального режима их работы, расчету и оптимизации параметров реактивных элементов согласующих цепей, при использовании которых требуемый режим возможно реализовать.

рассмотрением зарезонансного режима работы, поскольку он наиболее интересен в плане практического применения из-за отсутствия нелинейных эффектов при высоком уровне мощности СВЧ-сигналов.

Для произвольного идеального Y-циркулятора собственные значения матрицы импеданса Y-сочленения Z o+/— связаны с собственными значениями его матрицы рассеяния S o ₊/_ [3] соотношением (1)

^{1 + S} o + / - Гф 2пn )

Z o, + / - = i Р о — = ^- i Р о ^ct 9 |;; ⁺ ^l, (1)

• ^{1    S} o, + / - V^{2 3 )}

где p o — волновое сопротивление подводящих линий передачи; ф — фаза коэффициента прохождения сигнала со входа на выход; n = 0, +/-. Отметим, что Z o ₊j- , а также Z c , Z i и все импе-дансы, о которых говорится в тексте статьи, чисто мнимые.

В соответствии с (1) зависимости мнимой части собственных значений матрицы импеданса идеального циркулятора Z o ₊у- от ф в диапазоне 0 < ф < п имеют вид, приведенный на рис. 1.

Узкополосный циркулятор, из которого получается широкополосный циркулятор путем включения дополнительных цепей Z ₁ и Z_c , работает при ф = п. Это объясняется тем, что при ф = п схема узкополосного циркулятора имеет минимум элементов по сравнению с другими схемами узкополосных циркуляторов при ф * п, так как при ф * п собственное значение матрицы импеданса Z o * 0. Следовательно, для реализации требуемого значения Z ₀ необходимо вве-

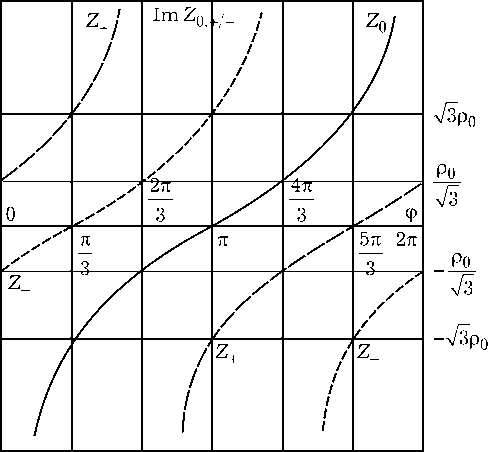
Рис. 1. Зависимость мнимой части собственных значений Z _0, + - матрицы импеданса от фазы коэффициента прохождения ϕ

	z;/ / /	Im Z+	1 1 / / / /ZL / /			7зр0 Ро
—			л		<р	7з
оз1	®3	со4	®2			03 Ро
					/	7з 7зр0
		77		/ / / / z'_! 1

Рис. 2. Зависимость мнимой части собственных значений Z + - матрицы импеданса узкополосного циркулятора от частоты ω

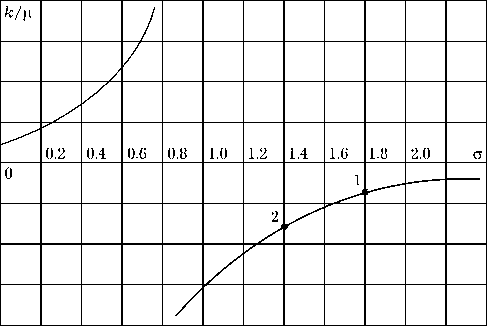
Рис. 3. Зависимость κ µ от σ

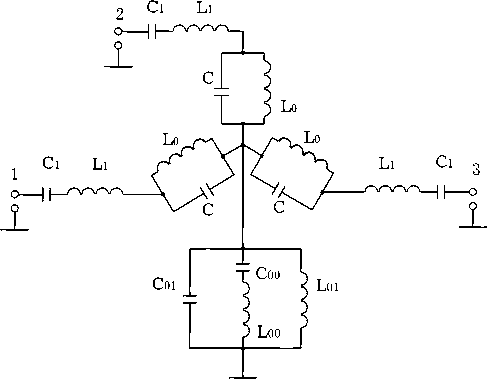
Рис. 4. Эквивалентная схема широкополосного Y-цир к улятора

дение дополнительных элементов. Зависимости мнимой части собственных значений матрицы импеданса узкополосного циркулятора Z +^' - от ω показаны на рис. 2 (ϕ = π соответствует частоте ω₂).

Согласно [3], условия циркуляции для узкополосных циркуляторов с ϕ = π и ϕ = 2π можно представить выражениями (2) и (3) соответственно:

² LC = 1,                     (2)

ω² LC = 1,                   (3)

µ2 - κ2

;

µ

ω L = - 3ρ₀ , ^µ

ω L = -

ρ 0      ,

3µ

где

L = ₂ L ₀µ _⊥ ;

µ ⊥ =

κ и µ – невзаимная и взаимная составляющие тензора магнитной проницаемости феррита µ .

Анализируя (2) и (3), можно сделать следующий вывод: при одинаковых ω индуктивность рамок L ₀ при ϕ = π в три раза больше, чем при ϕ = 2π, а емкости C при ϕ = 2π в три раза больше, чем при ϕ = π. Для остальных значений ϕ индуктивность и емкость принимают промежуточные значения. В зарезонансном режиме, при котором нормированное внутреннее поле подмагничивания σ = γ H_i ω > 1, величина κ µ является отрицательной (качественно представлено на рис. 3 [4]). Для реализации режима работы циркулятора, обеспечивающего наибольшую полосу рабочих частот при минимальном уровне прямых потерь, с учетом зависимости κ µ от частоты и соотношений (2) и (3) необходимо, чтобы циркулятор работал на верхней рабочей частоте ω₂ при ϕ = π (точка 2, рис. 3), а на ниж-

ней to i при ф = 0,2л (точка 1, рис. 3), т. е. о> 2 > to i и к/ц ( to 2 ) < к/ц ( to i ) .

Анализируя графики, приведенные на рис. 1 и 2, можно определить вид корректирующих цепей Z1 и Zc эквивалентной схемы циркулятора. В качестве Z1 необходимо использовать последовательный контур с резонансной частотой, настолько близкой к to2, чтобы на частоте ®2 отклонение от идеальных условий циркуляции, соответствующих ф = п, можно было не учитывать.

В качестве общей цепи Z_c необходимо использовать параллельно включенные последовательный и параллельный контуры, т. к. для частоты ® 2 с ф = п необходимо сопротивление общей цепи Z c = 0, а для to i с ф = 2п — соответственно Z c = ю. Эквивалентная схема широкополосного циркулятора представлена на рис. 4.

Для приближения условий циркуляции к условиям, обеспечивающим широкополосный режим работы в требуемом диапазоне частот, необходимо соответствующим образом выбрать значения элементов цепей Z ₁ и Z_c . Общая цепь Z_c позволяет получить практически любое значение импеданса без изменения условий циркуляции на частотах to i и к> 2 , в то же время при использовании в качестве Z ₁ последовательного контура значения элементов согласующей цепи Z ₁ не могут варьироваться без изменения условий циркуляции на частотах to_i и to₂ .

Анализ графика рис. 2 показывает, что при включении последовательного контура Z ₁, подобранного, как предложено выше, в каждое плечо циркулятора, на некоторой частоте to g , которая находится в интервале to i < to g < to 2 , величина Z _ будет равна 0. В то же время на частоте to₄, на которой Z ₊ = ю, можно получить условия циркуляции, соответствующие идеальным при ф = 2п/3, при соответствующей величине Z i , за счет уменьшения Z _ до уровня i V3"/3 р₀ , согласно (1). Наиболее подходящим является значение частоты to₄, при котором разница между Z ₊ и Z _ составляет в соответствии с (i) величину i V3p 0 .

Таким образом, подбором параметров контура Z ₁ могут быть достигнуты собственные значения матрицы импеданса Z ₊/_ , соответствующие условиям циркуляции, близким к идеальным, на частотах to i при ф = 0(2п), to 4 при ф = 2п/3. На частоте to 2 при ф = п значения Z ₊/_ будут соответствовать условиям циркуляции, близким к идеальным. На частоте to g при ф = п/3 значение Z _ будет

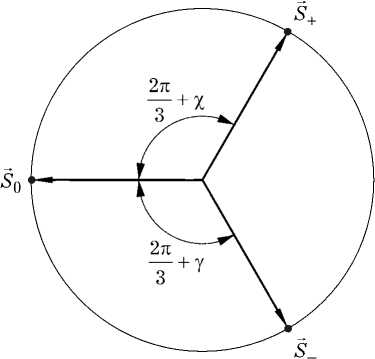
Рис. 5. Диаграмма собственных значений 5 ₊ , 5 _ и 5 ₀

соответствовать идеальным условиям циркуляции. За счет соответствующего подбора величин элементов общей цепи можно реализовать значения Z c таким образом, что на частотах to i , to 2 , to 3 , to 4 значения Z 0 будут близки к значениям, соответствующим идеальным условиям циркуляции. При несоответствии условий циркуляции на частоте to 3 идеальным необходимо изменить в небольших пределах величины элементов цепи Z ₁ таким образом, чтобы достичь близких к идеальным условий циркуляции, при этом допустимы небольшие отклонения от идеальных условий циркуляции на других частотах (to i , to 2 , to 4 )

Рассмотрим коэффициент отражения от каждого плеча циркулятора [5] в терминах собственных значений матрицы рассеяния

Г = ( 5 0 + 5 + + 5 _ )/ 3,                         (4)

где 5 0 , 5 ₊, 5 _ — собственные значения матрицы рассеяния.

На комплексной плоскости собственные значения 5 + , 5 _ и 5 ₀ можно отображать концами векторов 5 ₊, S _ и 5 0 , выходящими из начала координат (рис. 5).

Уравнение линии, вдоль которой коэффициент отражения имеет постоянное значение, в общем случае имеет вид

Г2п X - у)   Гп у)

i + 8 cos + —--- cos + х

3   2    32

, V .                                                (5)

х cos — +—Y = 9 |Г|2 ,

I3 2 J 1 1

где у, у — «углы расстройки», показанные на рис. 5.

На практике обычно |Г| < 0.i (углы расстройки X, Y малы), и уравнение (5) упрощается:

X 2 — XY + Y 2 = 9 |Г| 2 .                                   (6)

С помощью выражения (6), можно определить значения углов расстройки %, у, при которых коэффициент отражения |г| достигает своих максимальных и минимальных значений. Локальный экстремум, в котором значение коэффициента отражения минимально, достигается при X = Y. При этом векторы S ₊ и S - симметричны относительно S o . Очевидно, что минимизировать значение коэффициента отражения можно симметричным расположением любого из векторов S ₊, S - , S относительно двух других, Таким образом, при изменении параметров цепи Z ₁ для приближения условий циркуляции к идеальным на частотах № 3 , № 4 необходимо будет использовать при расчете вместо значений частот ю ^ , № 2 частоты № 1 , № 2 соответственно, на которых - Z ₊ = Z - , а на частоте № 3 оптимальная величина Z o должна быть равна - Z ₊,

• 2.    Расчет элементов эквивалентной схемы широкополосного Y-циркулятора

В соответствии с предложенной моделью широкополосного Y-циркулятора можно полагать, что эквивалентные схемы для возбуждений циркулятора собственными векторами U и U +- имеют вид, показанный на рис. 6.

С учетом (1) запишем условия циркуляции для произвольного циркулятора на частотах №₁ и № 2 соответственно (7) и (8):

' Z ₊ = i ТЗро/З;

Z - =- i V3 po/3;                              (7)

^z o =«,

^Z . = - i ^p :

< Z - = i V3 p o ;                                        (8)

• ^Z 0 = 0.

Собственные значения матрицы импедансов Z ₊ и Z _ для узкополосного Y-циркулятора с параллельным соединением емкостей C и индуктивностей рамок L ₀ определяются [3] соотношением

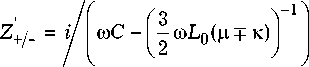
Собственные значения матрицы импедансов Z ₀ для широкополосного Y-циркулятора опре д еляются [6] по формуле

Z о = Z + 3 Z c .

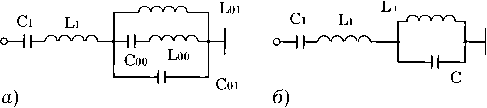
Рис. 6. Эквивалентные схемы широкополосного Y-циркулятора для синфазного возбуждения плечей циркулятора собственным вектором U о ( а ) и для возбуждений циркуля-

тора с правым и левым вращением электромагнитного поля собственными векторами U + и U - ( б )

Входящие в (10) Z ₁ и Z_c выражаются через реактивности L , C , L ₁, C ₁, L ₀₀, C ₀₀, L ₀₁, C ₀₁ (рис. 6)

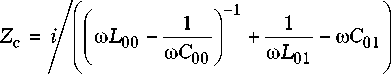
Z, = i № L - i ---, ¹          № С

Из соотношений (7), (8) с учетом эквивалентных схем рис. 6 можно записать условия циркуляции для широкополосного Y-циркулятора на граничных частотах рабочего диапазона № 1 и № 2 (13) и (14) соответственно:

• ' Z 1 + Z + = i 73ро/3;

• <    Z 1 + Z =- i V3p ₀/ 3;                          (13)

_ Z c = -.

Z 1 + Z + = i V3 p o ;

• <    Z 1 + Z - =- i V3 p o ;                            (14)

Z 1 + 3 Z c = 0.

Численное значение № 1 определяется следующим образом: по формуле (9) рассчитываются зависимости Z ₊ (№) и Z - (№); определяется частота № 1 , на которой, исходя из соотношений (8), разница между Z ₊ и Z - составляет i 2-V3/3 p o . Следовательно, из второго уравнения системы (13) Z 1 ( № 1 ) равно:

Г )

Z 1 =- I z - + i po I .                            (15)

На частоте № 4 , на которой Z ₊ = да, требуемая величина Z 1 определяется как разница между Z _ и Z - , которое, согласно (1), равно i V3/3p o . Следовательно:

Г                     1

Z 1 = I z - - i     po I ,                                (16)

По известным значениям Z ₁ ( №₁ ) и Z ₁ ( №₄ ) определяются величины L ₁ и C ₁

—

V

—

С =

(

V

—

. I . .73

i © 1 I Z — (© 1 ) + i — ро

_Л ¹

.

После нахождения величин L ₁ и C ₁

находятся

остальные значения элементов эквивалентной схемы, представленной на рис. 6, а , которые должны обеспечивать величину сопротивления Z о в соответствии с (1), т. е. Z о = ю на © 1 , Z о = о на © 2 , Z о =— i 73 р о на © 3 , Z о =— i V3/3 р о на © 4 . На частотах © 2 и © 4 сопротивление цепи Z_c мало, так как частоты © 2 и © 4 близки к резонансной частоте последовательного контура L ₀₀ C ₀₀, значит, ее сопротивление определяется в основном сопротивлением контура L ₀₀ C ₀₀. Пренебрегая сопротивлением параллельного контура

L ₀₁ C ₀₁, расчет элементов контура можно произвести

последовательного с достаточной точ-

ностью аналогично расчету Z ₁. В соответствии с (10) и C ₀₀ равны:

элементов контура (1) величины L ₀₀ и

( Г.

^L00 = i © 4

V

V

Л Л

— i Р о — Z 1 (© 4 ) I/3 77

—

^— © 2 ^{((— Z} 1 ⁽© 2 ⁾⁾/3⁾ I ⁽© 2 ^— © 4 ) 1 ,

C 00

⁽_2т        .7, .Va

VV

V1

Р о

—

Z 1

. (20)

При (11) ний

условии, находим L

что

01 и

L ₀₀

C 01 ,

и C ₀₀ известны, из из системы уравне-

для частот © 1

и

Z c = (— i 73р о — Z 1 (© 3 ))/3

Z c = *,

I © 3 ^L 01 = i

—

---—--+

^— i ^^р о ^— Z 1 ⁽© 3 )

V

+ i------ © 3 L 00

—

—

i

V1

—

,

^С о1 = ~ "

—

₊ 1 л

¹  © 1 ^L 01

.

Приведенная выше методика расчета позволяет приближенно определить значения элементов эквивалентной схемы циркулятора, обеспечива-

ющие условия циркуляции, близкие к идеальным на трех частотах. Для получения условий циркуляции, при которых величина |г| не превышает заданной величины в рабочем диапазоне частот, может потребоваться оптимизация параметров согласующей цепи Z ₁. Исходными данными для оптимизации являются численные значения элементов цепи Z ₁, рассчитанные выше, исходя из обеспечения близких к идеальным условий циркуляции на трех частотах © 1 , © 2 и © 4 . Задача оптимизации заключается в минимизации величины | Г | в диапазоне частот от © 1 и до © 2 посредством поиска оптимальных значений величин элементов цепи Z ₁. При оптимизации осуществляется уточнение значений L ₁, C ₁, при этом уменьшается величина |Г| на частоте © 3 , а на остальных частотах рабочего диапазона она увеличивается, после чего осуществляется коррекция значений частот © 1 , © 2 и рассчитываются L ₀₀, C ₀₀, L ₀₁, C ₀₁, при этом осуществляется уменьшение величины |Г| во всем рабочем диапазоне частот (© 1 , © 2 ). Оптимизацию в данном случае целесообразно осуществить с помощью методов прямого поиска [7], основанных на вариации значений L ₁, C ₁ и оценке соответствующих им значений |Г| в полосе частот (© 1 , © 2 ).

• 3.    Методика проектирования широкополосных Y-циркуляторов

Будем полагать, что исходными данными для проектирования циркулятора являются диапазон рабочих частот, величина обратных потерь в этом диапазоне и габариты циркулятора. При проектировании следует учитывать, что циркулятор должен работать при такой величине магнитного поля, которая обеспечивала бы достаточное удаление от области ферромагнитного резонанса. Проектирование включает в себя следующие этапы:

• 1.    Выбор ма р ки феррита по заданному диапазону рабочих частот.

• 2.    Выбор частоты © 2 вблизи верхней границы диапазона рабочих частот, задание значения величины ст = у H i /© > 1 на частоте © 2 и допустимой величины коэффициента отражения |Г| во всем диапазоне рабочих частот.

• 3.    Расчет величин L , C :

  • 3.1.    Расчет ц и к в диапазоне рабочих частот.

  • 3.2.    Расчет L ₀ и C из условий циркуляции (2) при ф = п на частоте © 2 .

  • 3.3.    Расчет Z ₊ / _—(©) по формуле (9) в полосе рабочих частот.

• 4.    Расчет частот ω₁, ω₃ и ω₄:

  • 4.1.    Определение частоты ω₁, на которой Z + ^' - Z ^' - = i 2 3ρ₀ /3, и по известным ω₁ и ω₂ проверка на соответствие полосе рабочих частот. При полосе меньше требуемой необходимо уменьшить величину σ и провести расчет по п. 1–4.1.

  • 4.2.    Определение частоты ω₄, на которой Z ₊^' = ∞.

  • 4.3.    Определение величин реактивностей L ₁, C ₁ последовательного контура по формулам (17), (18).

  • 4.4.    Определение частоты ω₃, на которой Z - = Z - ^' - Z ₁ = 0.

• 5.    Расчет элементов согласующей цепи Z_c по формулам (19), (20), (21) и (22).

• 6.    Расчет коэффициента отражения S ₁₁ в диапазоне рабочих частот по формуле (4) и проверка на соответствие заданным техническим требованиям.

• 7.    Оптимизация параметров согласующей цепи Z 1 :

  • 7.1.    Поиск оптимальных значений величин элементов последовательного контура в каждом плече L ₁, C ₁.

  • 7.2.    Определение частот ω^'₂ и ω₁^' (-( Z + ^' + Z ₁) = = Z - ^' + Z 1 ).

  • 7.3.    Расчет значений величин элементов цепи общего контура L ₀₀ C ₀₀ L ₀₁ C ₀₁ с учетом коррекции частот ω₁ и ω₂ до ω₁ и ω₂.

  • 7.4.    Расчет коэффициента отражения Γ в диапазоне рабочих частот по формуле (4) и проверка на соответствие заданным техническим требованиям. При соответствии величины Γ техническим требованиям – переход к п. 8, при несоответствии к подпункту 7.1.

• 8.    Разработка ТЗ на конструирование.

Заключение

Выполненные исследования позволили разработать методику проектирования широкополосных Y-циркуляторов на основе методов теории цепей. Она включает в себя два основных этапа: на первом этапе приближенно рассчитываются все численные значения элементов узкополосного циркулятора, параметров реактивностей цепей Z1 и Zc , исходя из обеспечения близких к идеальным условий циркуляции на трех частотах заданного диапазона, на втором этапе значения параметров реактивностей цепи Z1 уточняются посредством оптимизации.

Предложенная методика расчета была опробована авторами при разработке широкополосных Y-циркуляторов и вентилей метрового и дециметрового диапазонов длин волн. В метровом диапазоне длин волн макет развязывающего узла с размерами 45 × 50 × 20 мм³ обеспечивал обратные потери не менее 18 дБ при вносимых потерях не более 1,0 д Б в полосе рабочих частот не менее 45 ^, а в дециметровом диапазоне макет с размерами 17 × 24 × 14 мм³ обеспечивал обратные потери не менее 20 дБ при вносимых потерях не более 0,6 дБ в по л осе ра б очи х частот не менее 55 ^.