Проектирование силовых аддитивных конструкций: теоретические основы

Значительную часть искусственной окружающей среды составляют конструкции различного назначения. При разработке многих из них предъявляются требования достаточной прочности и жёсткости при минимуме массы. На протяжении всего развития цивилизации решение таких задач находится в триаде: материал – технология – конструкция. В зависимости от важности или новизны одного из этих компонентов устанавливается классификация конструкций: каменные, металлические, литые, клёпаные, сварные, тонкостенные и другие. Каждый из этих классов конструкций имеет свои специфические методы проектирования.

Совсем недавно появился принципиально новый метод создания конструкций – аддитивные технологии [1, 2]. Возможности этого метода и отдельных направлений его развития многообразны и сулят большой технический эффект [3]. Метод позволяет изготавливать конструкции из самых различных материалов: полимеров, металлов, керамики и всевозможных комбинаций из них [4]. Стало возможным производство монолитных конструкций с внутренними полостями, стержневыми структурами внутри оболочек и т.д.

Возникает вопрос: как наилучшим образом использовать эти новые возможности? На первых порах практическое внедрение аддитивных технологий началось с повторного изготовления существующих конструкций сложных форм, которые были ранее спроектированы по традиционным методам из изотропных материалов. Этот подход позволяет отказаться от таких сложных производственных технологий, как штамповка, литьё, сварка, механическая обработка и т.п. Однако, при этом новые технологические возможности аддитивных методов не используются в полной мере. Одна из причин такого положения состоит в том, что быстрое развитие аддитивных технологий не обеспечено должным образом теоретическими разработками. Здесь уместно напомнить известное положение из диалектики: «Теория без практики мертва, но теория указывает путь практике».

Возможности аддитивных технологий позволяют задуматься о создании сверхлёгких конструкций практически без оглядки на технологические ограничения. Поэтому, с точки зрения теории, интересно знать, как выглядит предел совершенства конструкций в каждом конкретном случае: при заданных геометрических ограничениях на размещение конструкции, условиях закрепления и действующих внешних воздействиях.

1 Задачи проектирования конструкций

В проектировании конструкций полезно выделить два основных вида деятельности: вы- бор структуры конструкции и выбор рациональных размеров её элементов. Первый вид проектной деятельности в русскоязычной литературе называется «выбор силовой схемы». Второй вид называется «параметрическая оптимизация» в связи с удобством формализации задач в терминах нелинейного математического программирования. Силовая схема предопределяет пути передачи сил. Назначение рациональных размеров элементов конструкции направлено на обеспечение условий прочности и жёсткости при минимальном расходе материала. В последнее время первый вид деятельности под влиянием зарубежной технической литературы стал обозначаться термином topology optimization – «топологическая оптимизация», а второй вид – sizing – «образмеривание».

В проектировании силовых конструкций до последнего времени существенную роль играет накопленный опыт и инженерная интуиция. Особенно это касается выбора структуры. Практика выработала два принципа проектирования, направленных на создание эффектив- ных конструкций.

Первый принцип – передача усилий по кратчайшим путям. Иногда это очень просто. Например, на рисунке 1а показана передача сосредоточенной силы P к заделке. Оптимальное решение – стержень, соединяющий точки А и B. При изменении направления силы P на некоторый угол, например, на 90°, выбор оптимальной структуры не очевиден.

а)

б)

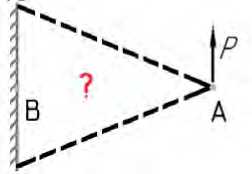
Рисунок 1 – Варианты передачи усилий в конструкции

Ещё сложнее принять решение, например, в трёхмерной задаче о выборе конструкции крыла малого удлинения. На рисунке 2 показаны два варианта решения по ориентации лонжеронов и стрингерного набора. В варианте а) прослеживается интуитивное стремление конструктора передавать воздушную нагрузку по кратчайшим путям, но при этом в длинных задних лонжеронах из-за малой строительной высоты будут возникать большие усилия в поясах. Не исключено, что схема б), которая организует передачу воздушной нагрузки через зоны крыла с большой строительной высотой, окажется более выгодной в весовом отноше- нии. Выбор оптимальной конструкции в этой задаче требует применения специальных методов [5].

Второй принцип , существенный для многих случаев нагружения, – эффективная работа одних и тех же элементов конструкции при различных вариантах нагружения. Второй принцип можно упрощённо сформулировать как обеспечение «взаимопомощи» элементов друг другу. Его хорошо иллюстрирует известная задача Разани [6]. Ферма, показанная на рисунке 3, нагружается либо силой P 1 , либо силой P 2 .

а) интуитивное решение

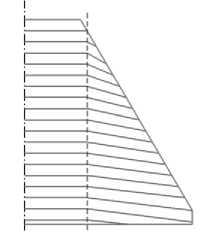
б) альтернативное решение

Рисунок 2 – Крыло малого удлинения

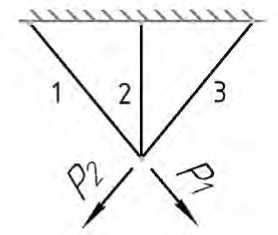
Рисунок 3 – Трёхстержневая ферма

Равнопрочная статически определимая ферма с двумя стержням 1 и 3 имеет массу больше, чем статически неопределимая неравнопрочная ферма со стержнем 2, который работает в обоих случаях нагружения и частично разгружает стержни 1 и 3 в каждом из случаев нагружения. Решение подобных задач на практике также требует применения специальных методов оптимизации.

2 Конструкции с минимальной потенциальной энергией деформации

Для демонстрации некоторых теоретических идей и методов поиска идеальных конструкций, которые могут быть эффективными в сочетании с практически неограниченными возможностями аддитивных технологий, рассмотрим задачу о проектировании конструкции с минимальной потенциальной энергией деформации [7-10]. Будем считать, что конструкция выполнена из ограниченного по массе m количества гипотетического материала c линейной зависимостью модуля упругости E и допускаемого напряжения [ ст ] от плотности р:

• (1)                                         E = р-E ,

• (2)                                                       [ ст ] = ст - р ,

где E и ст - модуль упругости и допускаемое напряжение при единичной плотности. Назначим некоторое количество материала m для создания 3D-модели, границы которой определяются заданными геометрическими ограничениями. Разобьём модель сеткой конечных твердотельных элементов. Предположим, что все исходные конечные элементы имеют одинаковые значения плотности и модуля упругости:

m

• (3)                                              ^р о i = V ’

• (4)                                                E о , = Р о ," E ,

где индекс 0 – начальное распределение материала, i – номер элемента, V – общий объём всех конечных элементов.

Рассматриваемую задачу оптимизации можно сформулировать как поиск конструкции с минимальной потенциальной энергией деформации при условии постоянства массы:

• (5)                            U —> min при m = const

Плотности конечных элементов будем рассматривать в качестве проектных переменных:

xi = pi, i = 1...n , где n - номер элемента в конечно-элементной модели. Проектные переменные pi ограниче- ны условием сохранения массы конструкции:

n

S Pi- V = m ,

= 1

где V i – объем i -го элемента.

Начальное (равномерное) распределение плотности материала в конструкции вычислим через объём конечных элементов:

P 0 i = ^m

n

■ S V i

V i = 1

Л-1

Рассчитаем напряженно-деформированное состояние (НДС) этой конструкции и вычислим эквивалентные напряжения в каждом элементе по удельной потенциальной энергии деформации:

• (9)    ^q = °1 + °2 + °2 - 2M°1 ■ °2 + °2 ■ °3 + °3 ■ °1)

Предполагая размеры элементов достаточно малыми, потенциальную энергию деформа- ции 3D-модели запишем в следующем виде:

n

° eqv о i

U = У

«2 ■ Pi" E

■ V

При вычислениях по (10) предположим также, что напряжения в конечных элементах остаются неизменными, в то время как плотности pi могут изменяться.

Воспользуемся методом множителей Лагранж а для поиска оптимальных значений плотностей элементов с учётом указанных допущений. Запишем следующую систему уравнений:

д U 1 дф

+ X"     — 0, (i = 1,2, dpi     dpi

n

...

, n );

^ ( p? ) = S p i^- V i ^{- m} = ⁰;

i = 1

где X - множитель Лагранжа, ф - вспомогательная функция, отражающая постоянство массы (7).

С учётом (10) получим:

^“

eqv _{0 i}    i

2 ■ E ■ p- n

+ X- V i = 0,( i = 1,2,

...

, n )

S p i- V - ^m = ⁰;

. i = 1

Откуда

^ρ 1 i ⁼

^σ eqv _{0 i}

2 ⋅ E ⋅ λ

Учитывая условие постоянства массы при изменении плотностей (7), новое распределение значений плотностей для каждого элемента запишем в следующем виде:

m

^ρ 1 i ^{= σ} eqv _{0 i} ^⋅ n

Усг -к

∑σeqv0i i i=1

где ρ _{1 i} - новое распределение плотностей, используемое в дальнейшем в итерационном процессе вместо исходного ρ 0 i . Отметим простой физический смысл (14): новые плотности элементов назначаются пропорционально действующим в них напряжениям.

Новым плотностям соответствует потенциальная энергия деформации U 0 1 , определяемая напряжениями σ eqv . Потенциальная энергия U 0 1 вычисляется путём подстановки плотностей ρ _{1 i} в (10). Начальное значение потенциальной энергии U 0 конструкции определяется напряжениями σ eqv и плотностями элементов ρ 0 i . Новое значение потенциальной энергии U 0 _- 1 , исходя из смысла решения оптимизационной задачи (11), будет меньше, чем исходное:

(15)                                           U 0 > U 0 - 1

При этом 3D-модель с распределением плотностей ρ 0 i даёт распределение напряжений σ 0 i , которое соответствует условиям равновесия и совместности деформаций. В теле переменной плотности (ТПП) с другим распределением плотностей ρ _{1 i} распределение напряжений σ 0 i удовлетворяет только условиям равновесия, но не совместности деформаций.

Распределению плотностей элементов ρ _{1 i} соответствует распределение напряжений σ 1 i и потенциальная энергия U 1 . В соответствии с принципом минимума энергии деформации:

^U 0 - 1 ^{>  U} 1

Перерасчёт плотностей элементов по (14) и НДС, при котором новое распределение плотностей используется в качестве исходных данных, приводит к последовательности конструкций с потенциальными энергиями

(17) U ₀ > U _{0 - 1} > U ₁ > U _{1 - 2} > U ₂ > ...

Эта монотонно убывающая последовательность ограничена снизу, поскольку энергия деформации величина положительная. Снижение значения потенциальной энергии до минимально возможного значения представляет собой поиск такого распределения плотностей, при котором конструкция обладает максимальной жёсткостью.

В процессе оптимизации плотности некоторых элементов могут обратиться в ноль, т.е. произойдёт вырождение элементов. При этом интенсивность деформации в невырожденных элементах становится одинаковой. Рассмотрим расчёт интенсивности деформаций в каждом элементе i на j+1 итерации с учётом новых плотностей, определённых по (14):

^ε j + 1 i ⁼

n

σeqvj+1i      σeqvji    i i =1

m ⋅ σ _eqvji ⋅ E

Когда напряжения c _{eqv r} становятся достаточно близкими к напряжениям c _eqv , процесс сходится, и получается следующее выражение, характеризующее интенсивность деформаций

во всех невырожденных элементах:

n

L ^C q Z ^V i

^,A= —---=--* const j       m • E

Основное расчётное соотношение итерационного алгоритма (14) при достижении сходимости, т.е. достаточно малых изменений напряжений и плотностей в каждом элементе, можно записать следующим образом, опустив номера соседних итераций:

^ eqv i P i

E с    V .

—------« const

m

Откуда следует, что найденное решение представляет собой равнонапряжённое в смысле гипотезы (2) ТПП.

ТПП с минимальной энергией деформации обладает ещё одним интересным и полезным для практических приложений свойством. Выберем из последовательности (17) «промежу-

точные» значения энергии

U 0 - 1 >  U 1 - 2 > ...

,

которые также образуют сходящуюся последовательность. Запишем выражения для этих величин, используя подстановку (14) в (10):

2 • E • m

(

• ^ c^ qq o о .

V i = 1

^ 2

• V

>

2 • E • m

(

• E ^ eqv i i

V i = 1

• V i

^ 2

> ...

n

Обозначим переменную величину E^eqv ' Vi в последовательности (22) символом Gj, i=1 j где индекс j обозначает номер итерации, и будем называть её силовым фактором, следуя [11] – «load carring factor» (LCF).

В процессе оптимизации эти величины также образуют сходящуюся последовательность

G 0 > G 1 > ^и достигают минимума в конструкции с минимальной энергией деформации.

Если не использовать конечно-элементных представлений, то величину силового фактора можно определить в общем виде как интеграл от эквивалентных напряжений по объёму конструкции:

• (23)                                            ^G = J ^CT eqv ‘ d^V

V

Силовой фактор учитывает одновременно величину внутренних усилий в конструкции и протяжённость их действия.

В простейшем случае стержневой конструкции (фермы) силовой фактор – это сумма модулей усилий N в стержнях, умноженных на их длину l

n

• (24)                                           G ,™„ = EI ^ f l' l .

i = 1

Через силовой фактор и допускаемое напряжение [ с т ] может быть вычислен теоретически необходимый объём V т стержневой или тонкостенной конструкции из традиционного материала или теоретически необходимая масса _т конструкции из материала переменной плотности со свойством (2)

V = —

^T    [ CT ]

G m_T = — ст

Чем меньше силовой фактор, тем конструкция легче. Вычислительные эксперименты показывают, что силовой фактор стержневых и тонкостенных безмоментных конструкций определяется в основном силовой схемой и относительно слабо зависит от распределения материала. Силовой фактор трёхмерных конструкций из материала с переменной плотностью сильно зависит от распределения плотностей и может уменьшаться на десятки процентов в процессе оптимизации. Интегральная величина – силовой фактор – позволяет построить эффективные, так называемые «весовые формулы», для прогнозирования и сравнения массы конструкций на ранних стадиях проектирования [12].

3 Топологическая оптимизация пространственных конструкций

На основе рассмотренного решения задачи о минимизации потенциальной энергии конструкции переменной плотности может быть предложен следующий эвристический алгоритм топологической оптимизации с учётом ограничений по прочности при многих случаях нагружения.

• 1)    В геометрические ограничения конструкции вписывается непрерывная упругая среда, разбиваемая сеткой конечных элементов типа “solid”.

• 2)    Задаются начальное распределение материала во всех элементах конструкции и минимально допустимая величина плотности элементов ^{P min} . Удобно использовать ^{Р о}i = const >  ^p mm , здесь индекс о - номер итерации. ^{P mn} может быть достаточно малой величиной, необходимой только для вычисления НДС ТПП.

• 3)    Вычисляется масса конструкции

n

• (27)                                        m o = Е Р о , " V

i = 1

.

• 4)    Назначаются механические характеристики элементов.

• 5)    Вычисляются по (1) и (2) удельные характеристики прочности ̅ и упругости предполагаемого к использованию конструкционного материала.

• 6)    Выполняется расчёт НДС трёхмерного тела на заданные внешние нагрузки.

• 7)    Вычисляются эквивалентные напряжения по определенной теории прочности, например по Мизесу, в каждом элементе для каждого случая нагружения

• ⁽²⁸⁾                            ^qv = V ^ст 2 + ^ст 2 + ^ст 3 ^-( ^СТ 1 ' ^СТ 2 + ^ст 2 ' ° "3 + ° "3 ' ° "1 )

и выбираются максимальные CT _eqv   , где j - номер итерации, i - номер элемента.

• 8)    Вычисляется интегральная характеристика – силовой фактор G n

• (29)                                     —, = E CT .V   < V

j            eqvmax ji i=1

• 9)    Определяются избытки прочности каждого элемента

  
  

Р ji ‘ ^CT n ji = —--- ст ^CT eqv max ji

Значения ^ ji <  1 означают недостаточную прочность i-го элемента.

• 10)    Выбирается минимальное значение п j min по всем элементам, и пропорциональным изменением плотностей всех элементов определяется потребная по прочности масса конструкции:

  _* m_j m j = ——

  П j min

  
  

• 11)    Вычисляются новые плотности элементов

  
  

  ^Р j + 1 i

  
  

  ^G eqv max, ji

  CT

  
  

• 12)    Если ^{P j + 1 i} <  ^{P min} i , то принимается ^{P j + 1 i   P min} i

• 13)    Вычисляется масса конструкции m 1 с плотностями элементов р 1 i ( р j ₊₁ i и масса m j в итерационном процессе):

n

• (33)                                   m 1 = £ Р1Г V

i = 1

Эту величину можно назвать массой «условно равнопрочной конструкции», так как назначение новых плотностей по (31) вызывает изменение НДС конструкции и отклонение п j min от единицы.

• 14)    Вычисляются новые модули упругости и допускаемые напряжения элементов

• (34)                                                 E j + 1i= Pj + 1i- E

• (35)    H+1 i ⁼ P j + 1i" ^CT

• 4.1    Проектирование балки

Далее весь расчёт повторяется с п. 6 до стабилизации. Для контроля целесообразно использовать условие 1- ≤ , где - малая заданная величина, например 0,01 в инженерных расчётах. Сходимость данного процесса наблюдается через 10-30 итераций в зависимости от особенностей задач.

В завершение оптимизации анализируется распределение материала и главных напряжений внутри заданных геометрических ограничений проектируемой конструкции. По результатам анализа предлагается несколько вариантов конструкций, которые могут быть изготовлены традиционными способами или с использованием аддитивных технологий. Сравнение силового и весового совершенства вариантов целесообразно делать с использованием критериев (29), (30), (31) и (33).

Приведенный алгоритм описан с подробностью, которая позволяет использовать его для реализации новой проектной парадигмы concurrent design – «технология точного попадания», описанной в [9]. Обращаем внимание на использование в нём новых для конструктора понятий «силовой фактор», «условно равнопрочная конструкция» и включение в проектный итерационный процесс известного понятия «избыток прочности» из традиционных поверочных расчётов в технологии эволюционного проектирования. Все эти три понятия имеют чёткое математическое описание. Наблюдение за изменениями указанных критериев в итерационном процессе обладает, по нашему мнению, большим обучающим потенциалом.

4 Примеры

В качестве простого примера проектирования и изготовления аддитивной конструкции рассматривалась балка, предназначенная для испытаний на трёхточечный изгиб. Геометри- ческие ограничения балки, условия опирания, нагрузка и схема разбиения на элементы даны на рисунке 4. Здесь же показано распределение плотности материала на второй итерации. Оптимальное по критерию равнопрочности распределение плотности материала в ТПП показано на рисунке 5.

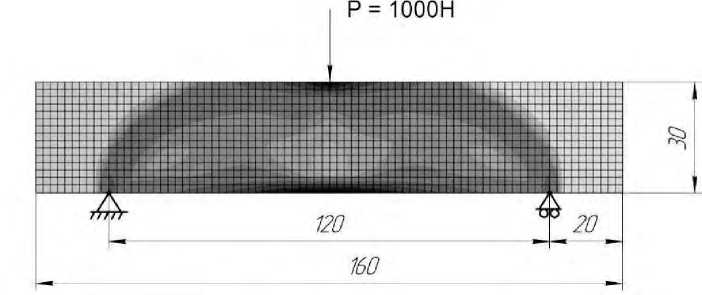
Рисунок 4 – Плоская проектная задача

Рисунок 5 – Распределение плотностей в элементах конструкции

Структура конструкции, показанная на рисунке 6, может быть выбрана по этой информации как рациональная. Силовой фактор этой фермы имеет величину G truss = 0,221x10 6 Н • мм, что превышает показатель равнопрочного ТПП G _тпп =0,201 x 10 6 на величину Д=9%.

На рисунке 6 показано испытание спроектированной и изготовленной аддитивной конструкции на трёхточечный изгиб до разрушения.

Рисунок 6 – Испытание рациональной аддитивной конструкции

Одновременно с фермой в едином технологическом процессе изготавливались стандартные образцы для снятия механических характеристик материала. Расчёт по методу конечных элементов разрушающего усилия для фермы по этим характеристикам дал удовлетворительное совпадение результатов.

Рассмотренная топологическая оптимизация плоских конструкций в настоящее время достаточно проработана для использования на практике. Другие возможные модели ТПП, отличные от (1) и (2), и интересные примеры решений можно найти в [13, 14].

Замечания о терминах.

В рассмотренном примере для описания эффективности проектов на вербальном уровне использованы термины «оптимальная» и «рациональная» конструкции. На наш взгляд, термин «оптимальная» уместно использовать когда чётко определены: целевая функция, проектные переменные и ограничения. Термин «рациональная» используется в современной технической литературе широко и не однозначно. Довольно часто он используется при принятии проектных решений с учётом многих факторов и многих параметров, которые хотелось бы получить в виде max или min. То есть речь идёт о компромиссах или множестве Парето, даже если оно и не упоминается ни в какой форме. В ряде случаев «рациональным» решением объявляется выбор из двух-трёх возможных вариантов. Поэтому в каждом конкретном тексте этот термин требует пояснений. Лучше всего, когда есть оценка предела совершенства, полученная из упрощённой или идеализированной задачи. Тогда о степени «рациональности» технического решения можно судить по «penalty» - уступке или недобору эффективности проекта по сравнению с идеалом. Например, коэффициент полезного действия тепловой машины определяет её эффективность по сравнению с идеальным циклом Карно. В нашем примере – это отношение реальной массы конструкции к теоретической, вычисляемой через силовой фактор.

• 4.2    Проектирование пространственной конструкции

  Рассмотрим пример проектирования пространственной конструкции для передачи крутящего момента М=10 8 Н ⋅ мм внутри прямоугольного параллелепипеда ABCDEFGH, с размерами AB=100, АD=500, АЕ=1000 (см. рисунок 7).

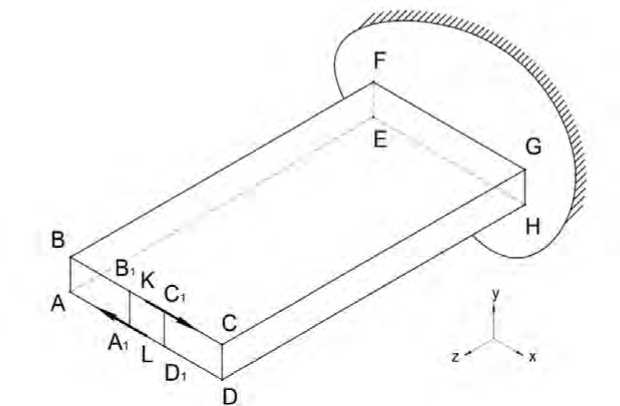
Рисунок 7 – Пространственная проектная задача

Нагрузка считается приложенной в виде пары сил в точках K и L. Закрепление конструкции возможно на площадке EFGH. Эта задача моделирует с определёнными упрощениями проектирование неподвижной части крыла самолёта с изменяемой стреловидностью. На ри- сунке 8 штриховкой выделена та часть крыла, в которой можно разместить силовую конструкцию. Вопрос в том, какой она должна быть?

В качестве простых решений задачи могут быть предложены интуитивно два варианта конструкций: а) круговая замкнутая цилиндрическая оболочка с поперечным сечением, вписанным в квадрат А1В1С1D1 и б) цилиндрическая оболочка с тем же прямоугольным попе- речным сечением.

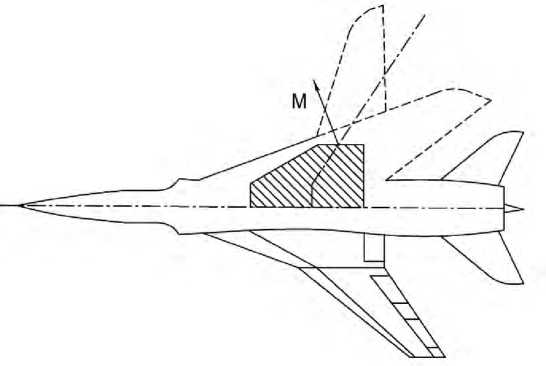
Рисунок 8 – Фрагмент силовой конструкции крыла с изменяемой стреловидностью

При расчёте касательных напряжений в этих оболочках по формуле Бредта и эквивалентных напряжений по Мизесу σ eqv = τ 7 3 получается одинаковая (!) величина силового фактора оболочек G = 3,46 ∙10 9 Н ⋅ мм для вариантов (а) и (б). Крутящий момент М в виде пары сил P=M/KL может быть передан на круговую оболочку с помощью кольца диаметром d=KL, материал которого работает с переменными усилиями в одноосном состоянии. Дополнительный силовой фактор кольца в задаче имеет величину Δ G = 1 M ⋅ π = 0,079 ⋅ 10 ⁹ Н ⋅ мм.

В итоге силовой фактор конструкции в виде цилиндрической оболочки с кольцом (шпангоутом) на свободном торце составляет G = 3,54 ⋅ 10 9 Н ⋅ мм.

Соответственно крутящий момент в виде пары сил может быть передан на квадратную тонкостенную оболочку с помощью торцевой стенки и пары стержней B 1 C 1 и A 1 D 1 с дополнительным силовым фактором Δ G = 0,137 ⋅ 10 9 Н ⋅ мм. Силовой фактор квадратной конструкции с зашивкой на свободном торце составляет G = 3,60 ⋅ 10 ⁹ Н ⋅ мм.

Таким образом, при одинаковых габаритах конструкция с квадратным сечением неожиданно оказывается несколько менее эффективной, чем круговая, несмотря на большую «световую площадь». Разница составляет менее 2%, и поэтому имеет только теоретический интерес.

Аналогичные расчёты тонкостенных конструкций с прямоугольными поперечными сечениями с соотношениями «ширины к высоте» B 1 C 1 /CD = 2/1 и BC/CD = 5/1 дают величины силового фактора конструкций соответственно G 2/1 = 2,79 ⋅ 10 9 и G 5/1 = 2,41 ⋅ 10 9 Н ⋅ мм.

Эти результаты также представляются несколько неожиданными – увеличение «световой площади» прямоугольных поперечных сечений в 2 и 5 раз даёт уменьшение силового фактора по сравнению с круговой и квадратной конструкцией только на 22,5% и 33% соответственно. В подобных ситуациях перебора вариантов конструкций представляет интерес знание предела совершенства – идеального решения.

С этой целью рассмотрим решение обсуждаемой модельной задачи с использованием алгоритма топологической оптимизации (раздел 3, пункты алгоритма 1-14). В качестве исходных данных использовались следующие характеристики конструкционного материала: плотность ρ=2,8 г/см 3 , модуль упругости Е=70000 МПа, коэффициент Пуассона μ=0,3, допускаемое напряжение [σ]=300 МПа. Эквивалентные напряжения вычислялись по критерию Мизеса. Расчёты НДС выполнялись в системе ANSYS с использованием кубических элементов Solid-65 с размером ребра 0,1CD. Узлы на плоскости EFGH считались закреплёнными по трём степеням свободы.

На рисунке 9 показано равнопрочное в смысле (20) распределение материала в конструкции. Эти картины отчётливо показывают, как крутящий момент в виде пары сил на первых 10% оси Z конструкции трансформируется через массивную часть в полую конструкцию переменного (увеличивающегося) сечения. Начиная примерно с 80% оси Z, передача крутящего момента в оптимальной конструкции постепенно перестраивается в бимоментную струк- туру у заделки.

Рисунок 9 – Оптимальное распределение материала

В качестве начального распределения плотностей принималась постоянная величина во всех элементах. На рисунках 10, 11, и 12 показано по итерациям j : изменение силового фактора G; массы условно-равнопрочной конструкции m j и массы потребной по прочности mJ; минимального коэффициента избытка прочности .

Потребность в довольно большом числе итераций объясняется «сильной» статической неопределимостью ТПП, представленного набором элементов. Изменение плотности и связанного с ней модуля упругости каждого элемента вызывает изменение распределения напряжений во всех остальных.

Величина силового фактора в полученной идеальной конструкции меньше, чем во всех рассмотренных интуитивно-рациональных конструкциях, таблица 1. Это означает её превосходство по способу передачи усилий.

Таблица 1 – Величины силового фактора

G квадрат , Н "  мм	^круг , Н "  мм	G прямуг.2 /1 , Н "  мм	G прямоуг. /1 1 , Н " мм	G 0 р t , Н " мм
3,60 ∙109	3,54∙109	2,79∙109	2,41∙109	2,29∙109

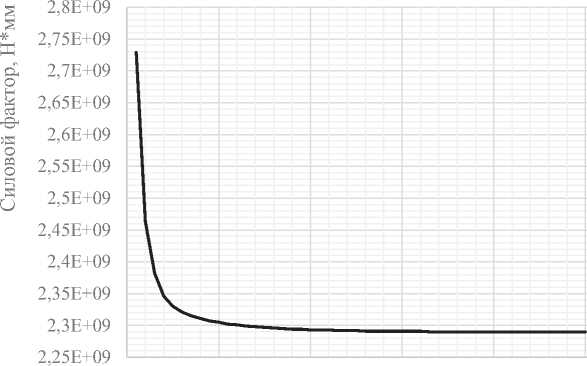
0         10        20        30        40        50        60

Номер итерации

Рисунок 11 – Изменение силового фактора в процессе оптимизации

34,00

32,00

30,00

20,00

28,00

26,00

24,00

22,00

Номер итерации

Рисунок 12 – Изменение масс в процессе оптимизации

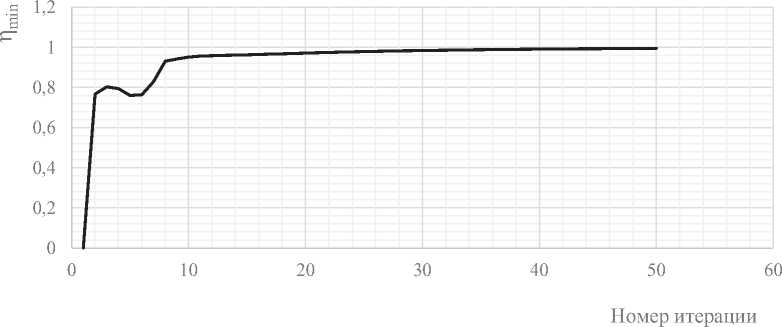
Рисунок 13 – Изменение минимального коэффициента избытка прочности в процессе оптимизации

Заключение

Рассмотренный алгоритм проектирования и примеры показывают, что оптимизационная модель в виде ТПП позволяет решать две самостоятельные задачи. Во-первых, получать количественную оценку предела совершенства конструкции с точки зрения минимизации её массы. Во-вторых, показать её рациональную силовую схему.

Пример с трёхмерной конструкцией показывает насколько перспективна разработка аддитивных технологий, которые позволяли бы создавать изотропные и анизотропные материалы переменной плотности в широком диапазоне её значений. На микроуровне это могли бы быть рациональные стержневые или ячеистые структуры с возможностями задавать поперечные сечения стержней и толщины ячеек. Заметим, что примерно так устроены такие совершенные конструкции, как кости животных, особенно птиц.

Работа выполнена при поддержке Министерства науки и образования Российской Федерации в рамках реализации программы повышения конкурентоспособности Самарского университета среди ведущих образовательных и научных центров на 2013-2020 годы.

Автор благодарит А.А. Павлова и С.А. Павлову за подготовку иллюстративных материалов.