Проектирование учебной дисциплины "Математика" в контексте требований образовательного стандарта к подготовке бакалавров технических направлений

усвоения, обеспечивающей математическую подготовленность студентов, достаточную для достижения заявленных образовательных целей.

Согласно федеральным государственным образовательным стандартам высшего образования содержание учебных дисциплин определяется самими учебными заведениями, которые, ориентируясь на примерные образовательные программы, примерные программы учебных дисциплин, разрабатывают и обновляют основные профессиональные образовательные программы. Такой подход, расширяющий самостоятельность вуза, составителя рабочей программы конкретной учебной дисциплины, в то же время требует ответа на вопрос: «Как в условиях общего сокращения времени на изучение учебных дисциплин и его существенного перераспределения в сторону самостоятельной работы студентов оптимизировать содержание обучения и уровни его усвоения для достижения предусмотренных стандартами образовательных результатов?»

Для реального выполнения требований стандартов разработчи- кам образовательных программ, составителям рабочих программ учебных дисциплин прежде всего необходимы:

• 1)    способы, процедуры установления более четких и обоснованных связей между составляющими содержания учебных дисциплин образовательной программы;

• 2)    однозначные формулировки уровней усвоения элементов содержания обучения (дисциплинарных целей), наиболее значимых для формирования компетенций студента и выпускника по конкретному направлению подготовки;

• 3)    механизмы оценки степени достижения сформулированных дисциплинарных целей.

Цель настоящей статьи – продемонстрировать возможный подход, позволяющий обоснованно проектировать учебную дисциплину «Математика» в системе подготовки будущих бакалавров по техническим направлениям.

Под проектированием учебной дисциплины нами понимается процесс определения содержания обучения, конкретизации образовательных целей и разработки сопряженного с ними оценочного механизма на основе объективированных методов анализа и дифференциации учебного материала, направленного на успешное освоение студентами основной профессиональной образовательной программы, достижение конечных целей подготовки.

Анализ нормативных документов, научно-методических работ и исследований, а также результаты поискового эксперимента привели к выводу о возможности проектирования учебной дисциплины «Математика» на основе системно-технологического подхода (А.А. Маши-ньян, Н.В. Кочергина, А.Ф. Ан и др.) [5, 1]. Применительно к задачам нашего исследования данный подход позволяет:

• 1)    в содержательном аспекте количественно обосновать значимость элементов математического содержания для успешного освоения общепрофессиональных и специальных дисциплин образовательной программы;

• 2)    в процессуальном аспекте выстроить последовательность процедур и алгоритмов конкретизации образовательных целей, выделения учебного материала, содержание и уровни усвоения которого студентами направлены на успешное освоение базовых и профессионально ориентированных дисциплин, достижение промежуточных и конечных целей подготовки.

Осуществление данного подхода при отборе содержания, выборе методов и средств обучения опирается на дидактические нормы, в качестве которых нами выделены принципы фундаментальности, профессиональной направленности обучения, внутри- и междисциплинарных связей.

Механизм реализации системнотехнологического подхода включает процедуры проектирования целей и содержания учебной дисциплины, основанные на применении объективированных способов анализа значимости учебных элементов. Результаты такого анализа позволяют исследователю, методи- сту, преподавателю принять решение относительно объема содержания обучения и уровня его усвоения, отражаемое в программах учебных дисциплин и содержании оценочных процедур.

Инструментом анализа, позволяющим получить количественные оценки значимости элементов содержания дисциплины «Математика», являются следующие использованные нами методы и процедуры.

• 1.    Анализ примерной программы дисциплины «Математика» для технических направлений подготовки с использованием метода матриц логических связей для получения количественных характеристик значимости элементов содержания – частоты использования и частоты обращения [4, 8]. Данный метод обеспечивает наблюдаемость экспертных решений и, таким образом, объективизацию отбора учебных элементов, выделения содержания обучения, наиболее существенного для усвоения с точки зрения системности и ориентированности на целостный конечный результат.

• 2.    Фиксация междисциплинарных связей дисциплины «Математика» на основе построения матриц логических связей математики с физикой и блоком профессиональных дисциплин. В результате выделяются элементы математического содержания, на которые опирается учебный материал базовых и профильных дисциплин. Например, для образовательной программы подготовки бакалавров по направлению «Радиотехника» такими элементами содержания являются темы «Векторы. Линейные операции над векторами. Скалярное, векторное и смешанное произведения векторов», «Дифференциал и производная функции», «Производные и дифференциалы высших порядков», раздел «Интегральное исчисление функций одной переменной», раздел «Дифференциальное исчисле-

• ние функций нескольких переменных», «Ряды Фурье. Интеграл Фурье. Преобразование Фурье», раздел «Обыкновенные дифференциальные уравнения».

• 3.    Проводится опрос ведущих преподавателей общенаучных и выпускающих кафедр для получения экспертных оценок значимости элементов содержания математики для освоения студентами базовых и профессионально ориентированных дисциплин. В нашем исследовании профессорско-преподавательскому составу кафедр, участвующих в реализации образовательных программ по направлениям «Радиотехника» и «Приборостроение», предлагалось по пятибалльной шкале (1, 2, 3, 4, 5) оценить каждый элемент содержания дисциплины «Математика» из списка тем примерной программы относительно степени его значимости в профессиональной подготовке бакалавров радиоэлектронного профиля. В результате обработки данных опроса 34 респондентов каждому элементу математического содержания ставилась в соответствие средняя оценка его значимости.

В результате анализа выделены учебные элементы математики, на усвоение содержания которых (по показателю частоты использования) опирается большее число тем по сравнению со средним значением частотности (0,2) [1]. К ним относятся темы «Множества.

Математика – базовая дисциплина инженерно-технического образования по всем направлениям и специальностям

Действительные числа. Функция» (0,74), «Числовые последовательности. Предел функции. Бесконечно малые функции. Эквивалентные функции» (0,6), «Дифференциал и производная функции. Производная сложной и обратной функций» (0,52), «Неопределенный интеграл. Основные методы интегрирования» (0,8), «Определенный интеграл. Формула Ньютона – Лейбница. Вычисления интегралов» (0,47); «Дифференциальные уравнения первого порядка» (0,5) и некоторые другие.

Анализ показал, что в видении экспертов приоритетными для освоения профессионально ориентированных дисциплин являются элементы содержания математики, относящиеся к разделу «Линейная алгебра и аналитическая геометрия» в части операций над векторами (средняя оценка значимости 4,0), «Дифференциал и производная функции» (4,6), «Неопределенный интеграл. Основные методы интегрирования» (4,7), «Определенный интеграл. Вычисления определенных интегралов» (4,8), «Дифференциальные уравнения первого порядка. Задача Коши» (4,5), «Дифференциальные уравнения высших порядков. Линейные дифференциальные уравнения» (4,5) и др. Следует отметить, что умения применять аппарат дифференцирования и интегрирования функций создают условия для успешного изучения студентами не только дисциплин

Наш любимый Муром-городок

математического блока и физики, но и профессионально ориентированных курсов – «Электромагнитные поля и волны», «Электродинамика и распространение радиоволн», «Радиотехнические цепи и сигналы» и др. Значительным прикладным потенциалом обладают темы «Комплексные числа» (4,4) и «Функции комплексной переменной» (3,9), являющиеся математическим инструментарием дисциплин «Основы теории цепей», «Радиотехнические цепи и сигналы», «Функциональное моделирование радиоэлектронных устройств».

Сравнение количественных оценок значимости элементов математического содержания по результатам опроса преподавателей, анализа матриц логических связей математики с дисциплинами образовательной программы, собственной матрицы логических связей дисциплины «Математика» позволяет обоснованно дифференцировать совокупность учебных элементов математики, необходимых для успешного освоения общепрофессиональных и специальных дисциплин. Следовательно, в рамках отве- денного бюджета времени целесообразно существенное увеличение его доли на усвоение студентами выделенного содержания обучения, которое должно быть усвоено в учебном процессе на достаточно высоком уровне.

На основе анализа оценок значимости учебных элементов математики отбирается комплекс заданий для использования на практических занятиях, при самостоятельной работе студентов, в содержании оценочных процедур. В него помимо типовых учебных задач по математике входят задания, для выполнения которых требуются умения применять усвоенные математические методы, процедуры и алгоритмы в нетиповых, субъективно новых для студентов условиях. Такие задания рассматриваются нами и как мотивационно значимое средство обучения, стимулирующее активное освоение учебного материала (предполагающее продуктивную деятельность), и как дополнительный инструмент оценочных процедур, позволяющий определить степень усвоения наиболее значимого математического содержания. На- пример, студентам, обучающимся по направлениям радиоэлектронного профиля, на практических занятиях, при самостоятельной работе могут предлагаться следующие задания:

• 1.    В электрической цепи резистор подключен к выводам источника постоянного тока, электродвижущая сила которого ε и внутреннее сопротивление r . Оцените, при каком значении сопротивления R резистора выделяющаяся на нем мощность будет максимальной?

• 2.    Электрический проводник имеет форму лепестка, ограниченного дугами окружностей ( х – 2)² + у ² = = 4, х ² + ( у – 2)² = 4. Определите площадь лепестка.

• 3.    Изолированному проводнику сообщен заряд q ₀. Вследствие несовершенства изоляции проводник постепенно теряет заряд. Скорость потери заряда в данный момент пропорциональна наличному заряду проводника. Определите, какой заряд останется на проводнике по истечении времени t , если за первую минуту потерян заряд Q .

С учетом работ Б. Блума, В.П. Беспалько, В.М. Соколова [7], для диа-

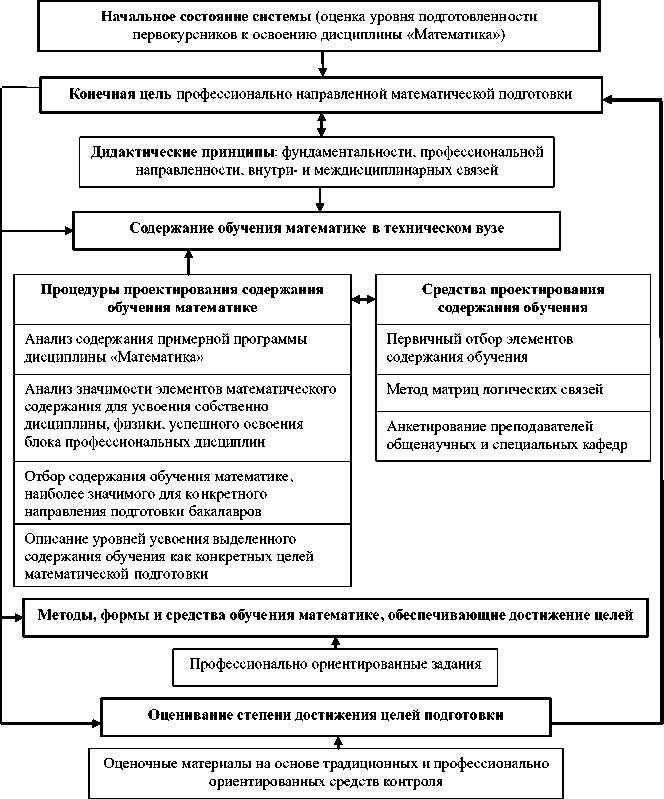
Модель методической системы подготовки по математике в техническом вузе

гностики степени усвоения содержания обучения математике предлагается механизм, включающий:

– таксономию уровней усвоения содержания обучения, ориентированную на повышение объективности оценивания результатов подготовки с дифференциацией деятельности обучающегося [3]. Раскрыты основные признаки усвоения учебного материала на уровнях узнавания, воспроизведения и применения математического содержания, способов действий в привычных условиях (репродуктивная деятельность) и использования ранее усвоенной информации, способов действий в новых, нетиповых для субъекта ситуациях, условиях (продуктивная деятельность);

– оценочные материалы на основе традиционных (задания в тестовой форме, учебные задачи)

и профессионально направленных средств контроля, при отборе которых учитываются результаты оценок значимости элементов математического содержания для фундаментальной подготовки и успешного освоения блока профессиональных дисциплин.

Предлагаемый подход реализован в рамках методической системы обучения математике студентов технического бакалавриата, модель которой приведена на рисунке. Выделим некоторые особенности системы.

Первое. Оценка уровня подготовленности первокурсников к освоению дисциплины «Математика».

Отсутствие в результатах единого государственного экзамена информации о том, какие именно задания выполнил ученик, не позволяет преподавателям, обучающим сту- дентов на первом курсе, судить об уровне их подготовленности к усвоению конкретных разделов вузовской математики. Для определения этого уровня выполняется процедура входного контроля. При отборе содержания оценочных заданий акцент делается на учебные элементы с высокой частотой использования и темы, которые в первую очередь необходимы для успешного освоения вузовского курса математики.

Второе. Описание конкретных (семестровых, внутрисеместровых) целей математической подготовки, сопряженных с соответствующими оценочными средствами на основе предложенной таксономии уровней усвоения содержания обучения [3].

Согласно этому описанию, студент должен демонстрировать:

– узнавание учебного элемента (определения, понятия, правила, утверждения, теоремы, алгоритма) среди совокупности близких по содержанию (смыслу) учебных элементов;

– умение использовать с опорой только на собственную память математические процедуры, алгоритмы и методы, наиболее значимые для освоения базовых и профессионально ориентированных дисциплин;

– умение обоснованно применять базовые математические понятия, процедуры, алгоритмы, методы для решения прикладной задачи;

– умение использовать математическую модель исследуемого объекта, давать математическое обоснование принимаемого решения.

Третье. Отбор содержания обучения математике для конкретного направления подготовки с учетом количественных оценок значимости учебных элементов по результатам анализа матриц логических связей и экспертных оценок преподавателей.

Четвертое. Перераспределение времени, выделяемого на практические занятия и самостоятельную работу студентов в сторону увеличения его доли на усвоение выде- ленных элементов математического содержания.

Пятое. Использование с учетом оценок значимости учебных элементов профессионально направленных заданий на практических занятиях, при самостоятельной работе студентов, в содержании оценочных процедур.

Предлагаемый подход к совершенствованию подготовки по математике в техническом вузе позволяет методистам, преподавателям количественно оценить значимость и обоснованно выделить учебный материал дисциплины «Математика», содержание и уровни усвоения которого направлены на успешное освоение профессионально ориентированной части обучения по конкретному направлению бакалавриата, формирование предусмотренных федеральными государственными образовательными стандартами компетенций выпускника.