Проективно-евклидова связность в изображении горизонтальных плоскостей

В статье продолжается обсуждение общей теории перспективы Б. В. Раушенбаха. Показано, что проективно-евклидовы связности (сохраняющие геодезические) в изображениях горизонтальных плоскостей как при классическом центральном проектировании на картинную плоскость, так и при проектировании на сферу с последующей разверсткой в квадрат, не являются даже эквиаффинными. Рассмотрены возникающие при этом билинейные формы и линейные операторы в изображении.

Б. В. Раушенбахом экспериментально подтверждается, что зрительное восприятие пространства и плоскостей в нем существенно искажает прямые линии в кривые (в отличие от классической теории перспективы, основанной на центральном проектировании пространства на «картинную» плоскость) [3]. Эти данные позволяют выделить зоны прямой и обратной перспектив. В зоне обратной перспективы евклидова плоскость, по утверждению Б.В. Раушенбаха, изображается плоскостью Лобачевского постоянной отрицательной кривизны. Это подразумевает, что прямые — геодезические аффинно-евклидовой плоскости изображаются геодезическими в образе, что приводит к задаче привнесения, по крайней мере, аффинной связности в зрительный образ за счет проектив-ного(геодезического) отображения [2, с. 165] евклидовой плоскости. Для этого нужна полная математическая модель отображения, что мы и делаем на основе работы [1].

• 1.    Общие замечания по нахождению проективно-евклидовой связности.

Рассматриваются отображения горизонтальных плоскостей z = Z 0 * 0 (абсолютно симметрично выглядят отображения вертикальных плоскостей у = у 0 * 0):

• —    на плоскость Оху (при h = 1), которое описывается формулами (ось О^ = Оу, О р = Oz):

и               z .

^ = ——, П =----, х +1 > 0;   (1)

х + 1 х + 1

• —    на сферу с последующим отображением проекции на квадрат О ^п , X = 1 формулами:

^ = arctg , р = arctg —, х + 1 > 0. (2) X + 1 х + 1

Системы координат Oхуz, О^, О^р — прямоугольные в Е 3 , на картинной плоскости ^ 2 и в квадрате

л

--<

Я

^ <  2

к л

,

^^^^^.

— < п < —

2        2

соответственно. Заметим, что при отображении (2) точки р = 0 отвечают бесконечно

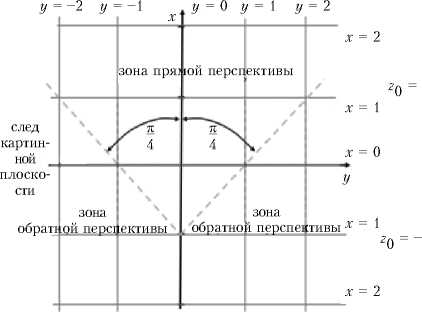
удаленным точкам горизонтальных плоскостей z = Z o (линия горизонта), а граничные точки квадрата — предельной «рамке» изображения (рис. 1).

В силу двухмерности многообразий тензор кривизны заменяется тензором Риччи:

R = RS..=3IS     S

^ij    ^Sij иs1 ij Ui1 Sj + s k s k

^{+ 1} sk ¹ ij ¹ ik ¹ sj ■

На исходной «горизонтальной» плоскости z = z o * 0 введем координаты точки М:

х¹ = х + 1 >  0, 2

_^х  = у.

У = ^-1

а) изображаемая полуплоскость

л

У = -2

У = ²

линия след картин!

У = 1

;лед картинной плоское

- 2

ой 1

■ горизонта У = О

2 = 2 о (х + 1 геодезической

> О) с координатной сетью

б) изображение полуплоскостей 2 = 1 и 2 = -1 с координатной геодезической сетью

на

плоскости О<;ц

У = О

У = 3

X =

X = у =

X = л 3 2

^У = 3

У =

2 у = 1

2 = 1

2 =-1

У =

О

О

■ зона прямой перспективы

У =

У =

-1,5

линия горизонта

предельная «рамка» изображения

в) изображение полуплоскостей 2 = 1 и 2 = -1 с координатной геодезической сетью в квадрате О ^ц

Рис. 1

Прямоугольные координаты в изображении точки М:

функции — класса С2 с якобианом, отличным от нуля. Уравнения геодезических пря-

^^в

^^в

и¹ = и¹(х¹х²),

2    2  12

и = и Ст х ).

мых с геодезическим параметром t имеют вид:

х¹ = b^lt + x Q

При этом предполагается,

что эти

Не предлагая геодезичность параметра t за-

ранее, из уравнения геодезических линий в изображении d^u1     ь du du1   . du1

г Гц= X dt2      7 dt dt       dt с учетом (6 — 7) приходим к тождествам по Ьг:

[d_i}u^k + r¹_pd_iu^sd j U ^р ) b*b³ = ( Х д^¹ ) b¹ .

Из них следует, что:

• 1.    X = 0, т. е. параметр t — геодезический в изображении.

• 2.    Э^ ур* + Г ^р 8^y u^s 6 у уи ^р = 0 — уравнение для нахождения коэффициентов Г ¹ связности.

С учетом симметрии d ij U^k и переброса симметрирования по 1, / на s, р последние уравнения принимают вид:

д;м¹ + Г ¹ diu^sд ,и ^р = 0.       (8)

Ч          ( sp ) ¹ J

Из уравнения (8) ясно, что Г ¹ не определяются однозначно и требуется задание тензора кручения. Поэтому мы будем искать сразу симметрическую аффинную связность из соотношений:

^R = ( ^Rd ) =

д ^у U + Г ^рд^ и⁵ д у и ^р = 0,

Г * = Г* 5р      р5 .

2. Геометрия изображения плоскости

z = Z o * 0 на картинной плоскости.

С учетом (5) при центральном проектировании (1) горизонтальной плоскости на картинную формулы (6) принимают

вид:

¹ = ^р u² = ^, х¹ >  0.     (10)

Вычисляя Г ¹ из (9), находим, что

X

Г

^z 0

2x j ^z 0

остальные Г ¹ = 0.

Из формул (4) находится тензор Риччи:

(

^^^^^.

I ^г 0

^z 0

t *¹ ) ²

г 0

, „    2    „

Д = det R = — > 0.

^г 0

Таким образом, уже при классическом центральном проектировании геометрия горизонтальной плоскости не является даже эквиаф-финной, т. е. при параллельном переносе в проективно-евклидовой связности (11) площади не сохраняются, хотя геодезические остаются прямыми с сильно искаженной метрикой и без сохранения параллельности.

Билинейная форма тензора Риччи (12) оказывается эллиптического типа, а его симметрическая часть с матрицей

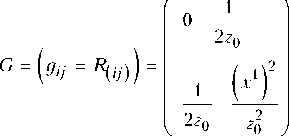
g =--- < 0 — гиперболического. (13)

4 ^z q

Билинейные формы R и G порождают одну и ту же квадратичную

ф (а) = Д2 zo L

1 2 z ^ a а

+ ( д ¹ ) ² ( а² ) ²

и конус изотропных (самосопряженных) направлений состоит из двух прямых:

1) я2 = 0 (образ прямых || Ох);

2)Д =- ^ . 2 ^z 0

Учитывая, что косая часть R

^Е = ( ^еч = ^КЫ )

— ( 0 ,1

2zo ^ 1 0J

тоже порождает невырожденную билинейную форму, на картинной плоскости в координатах (х1, х2) возникают линейные операторы с матрицами:

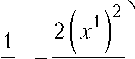
3      3z0

Л = s - ¹G =

I

В = s ^ R =

^^^^^M

2 I

,

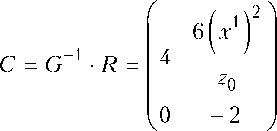
с очевидными зависимостями В = E + А, С = Е + А^-1 и им обратные. Заметим, что собственными векторами всех этих операторов служат векторы изотропных направлений квадратичной формы ф ( а ) .

На самом деле это вытекает из структуры матрицы R билинейной формы, т.е. если

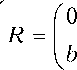
_   а + b Г О

, то G =

2 1 1

1 I

I , У )

2с где у =-----, а + b

а - b Г О 1 s =

2 ( - 1 О

и

Л = s^{- 1}G = —-

а + b Г 1 у

b - а I О - 1

собственные направления оператора А совпадают с изотропными направлениями квадратичной формы ф ( а ) и определяются векторами

- Г¹) - Л) р = и р₂ = • ¹ ( 0 ) ² ( - 2 )

В силу структуры матрицы А этот линейный оператор порождает единственный скалярный инвариант

J = det А

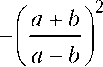
< О

вне зоны ti² - b² = 0,     (18)

т. е. оператор А меняет ориентацию на противоположную и площади умножаются на 2

Г а + Ь )

а — Ь

•

3. Геометрия изображения плоскости z = z ₀ ^ 0 на квадрат О^ц.

В данном случае формулами изображения служат

1          , . ^х 2               2        1

и = arctg —, и = arctg -°, х >  О

и аналогичные вычисления дают значения Г , R:

Г

Г

2х 2

Г 12

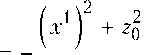
^{х 2} О

22 = ^-

2Х1

² О

остальные Г = О,

^ 0 ^- ( ^ ) ² - ²-^0

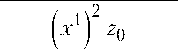
д =

2      )

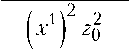
(Щг2

,

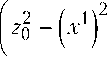
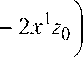
Геометрия по сравнению с п. 2 стала во многом более сложной, так как образ плоскости и прямых на ней ограничен, геодезические линии лишь в частных случаях (рис. 4, 6 [1] и рис. 1 в данной работе) прямолинейны (интервалы), при параллельном переносе площадь (косое произведение) не сохраняется, тензор Риччи — смешанного типа, и если обозначить х1 = Х0 > 0 — корень уравнения А = 0, то хо = -2О + V2 2о ,         (21)

зоны типа R в зависимости от х¹ и 2 0 (от х² они не зависят) делятся по признаку (рис. 2):

_е А < 0 _е А > 0 _х 1

^{0         х} 0

А < 0 — гиперболического типа;

А > 0 — эллиптического типа

Рис. 2

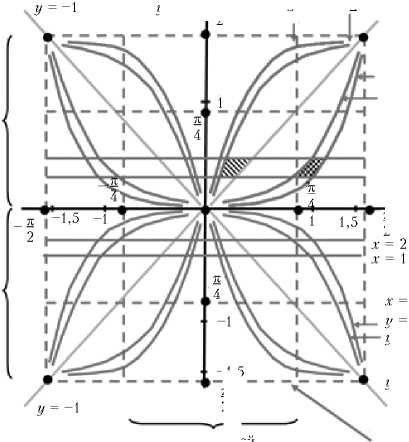
В квадрате О ^р это выглядит так (рис. 3):

^^^^^в д < д = д >

^^^^^в

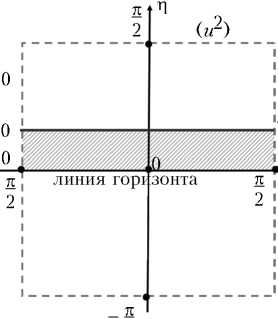
предельная «рамка» — изображения г0

п о = ^arcts — (² 0 >  ⁰ ) ^х 0

^ё («з

Рис. 3

Р 0

- arctg

Г ¹ 1

I 72 + 1 J

для Z 0 <  0,

Плоскости z = Z0 в R₃ этим зонам отвечают (рис. 4):

т. е. П 0 зависит только от знака Z 0 . Напоминаем, что Z 0 > 0 отвечает плоскостям выше уровня глаз, а Z 0 < 0 — ниже этого уровня.

Мы не можем дать какое-либо разумное физиологическое объяснение (в отличие от конуса перехода прямой перспективы в обратную в статье [1]).

Такая нессимметрия по знаку z скорее всего связана с построением модели на последнем этапе развертывания сферы в квадрат.

Математически никаких противоречий нет, так как уравнение Д = 0 в области с единственным ограничением х ¹ • Z 0 ^ 0 (т. е. включающее и проектирование Е 3 при х¹< 0) имеет корни

X

	•
	(ЖЖЖЖЖЖЖЖЖ д = х 0 д < 0
	' х2

Рис. 4

Х 0 = -Z 0 ± V2 ^ = -2 0 ( 1 ± V2) ,

<                ₂₍.                 ₁            (24)

Р 0 = arctg -° = ^-arctg

_            х₀          1 ± V2

Но в положительном полупространстве X i > 0 уравнение (24) дает разные значения

для х₀ и Р 0 :

На плоскости z = Z 0 положение X 0 ( Д = 0) зависит от Z 0 (и |^0|, и знака sign Z 0 ), но в

хо = koi (V2 - 1), < хо = ко (V2 + 1),

П о = arctg

П о = arctg

V2 - 1’ 1

V2 + 1’

2 о >  ^о ;

^г о <  ^о -

квадрате

(^

Р 0 = arctg

Г 1

I V2 - 1 J

При этом изображается полуплоскость (х¹ > 0, х²) при Z 0 > 0 в области квадрата П > 0, а при Z 0 < 0 — в области П < 0 (рис. 5)

для Z 0 >  0,

^^^^^в

^^^^^в

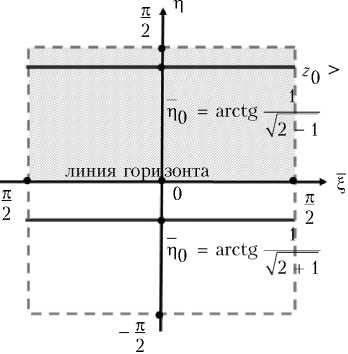
а) изображение ( х ¹ >  0, х ² ) при Z 0 > 0

Л	р
2
1                                                                                          1 1 1		1 z0 " 0 1 1
1 1 линия гори	зонта	1
л 1	0	1 л ^
2 |___________________________		_____1 2
।
		1 __1
л ^^^^^в   ^^^^^в

б) изображение ( х ¹ >  0, х ² ) при Z 0 < 0

Рис. 5

Из формул (16), (17) и (20) следует, что в данном случае

а + b

( ^{х 1} - ^z 0 ) ² 2 ( ^Х ) ² 2 о

Во всех точках вне запретных форма G — гиперболического типа, так как д = det G =

( а + b ) 2

( ^{х 1 - z} 0 )

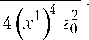
а - b _ ³ ( ^{х 1} ) ^{2 + 2 x 1 z} 0 ^{- z} 0 ^ _ ( ^{х 1} ) ^{4 -} ( ^z 0 ) ⁴

2           2 (Х) zo              (х1) z0

и поэтому

Скалярный инвариант (18) имеет значение

J =

-

( ^{x 1} - ^z o )

² ( ^¹ ) ⁴ - ^{( z} o ^{) 4 z} o ( ж^{1 - z} o ) ²

3 ( x¹ ) + 2x¹z o

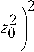
< o

при

1 , „ x * Z o

и x¹ * ^{- Z o + 2 |Zo1}

■

т. е. изотропные направления тензора Риччи определяются векторами

Р1 _

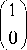
Р 2

(х1 + zo ) [( х1 )2

^{+ z} 0

^z 0 ( ^z 0 ^{- х 1} )

■ (26)

Вырождение симметрической части, G, про-

л исходит при X1 - Zo, П = и возможно только при zo > 0, а вырождение косой части, s, при других значениях:

_ж 1 _ ^{- z} o ^{+ 2}|^z o|

,

n o

= <

_ 3 arctg—

I zo|

1 arrtg — ^z o

при z o >  o,

при z o <  o.

Если этот инвариант считать скалярной кривизной в изображении плоскости z - Z o * o, то она отрицательна, но непостоянна, и геометрия только локально может быть приближена к геометрии Лобачевского.

Характер геометрии плоскости изображений лучше определять не глобальным свойством непересечения геодезических, а более локальным — дефектом геодезического многоугольника. В обсуждаемой нами модели существуют четырехугольники в плоскости О ^р , в которых сумма углов меньше 2 л , например, в образе прямоугольника А 1 (а, Ь), А 2 (2а, Ь), А з (2а, 2Ь), А₄(а, 2Ь), а в образе трапеции В 1 (а, Ь), В 2 (а, с), В-₃(ка, кс), В₄(ка, кЬ) сумма углов равна 2 л , так как этот образ — прямоугольник в плоскости О ^р .