Проективные симметрии пятимерных пространств

Работа посвящена обзору инвариантно-групповых методов в 5-мерных теориях электромагнитного, гравитационного и других физических полей. Обсуждается имеющая многочисленные геометрические и физические приложения проблема исследования многомерных псевдоримановх многообразий, допускающих алгебры Ли инфинитезимальных проективных преобразований, более широкие, чем алгебры Ли инфинитезимальных гомотетий.

Проективное преобразование псевдоримаиова многообразия М^п с проективиой структурой П сохраняет проективную структуру П и переводит геодезические линии снова в геодезические [1,56].

Векторное поле X на псевдоримаиовом многообразии (М, д) с проективной структурой П называется бесконечно малым проективным преобразованием, или проективным движением, если локальная однопараметрическая группа локальных преобразований, порожденная этим полем в окрестности каждой точки т е М, состоит из (локальных) проективных преобразований, т. е. автоморфизмов проективной структуры П.

(Zx.g"・),* = 2%)9,* + %* 9 j + gjk 屮",(I)

где 夕一 функция от т\ называемая определяющей фуикцией проективного движения X [1].

Уравнение (I) можно записать в виде двух соотношений:

(обобщенное уравнение Киллинга) и

九勿j,k = 2,仇j『\k + 仇k 夕,j + 9jkR〃

(уравнение Эйзеихарта). Если g = const, то есть div X = const, то век торное поле X сохраняет аффинную связность и, следовательно, является бесконечно малым аффинным преобразованием, или аффинным движением.

Аффинное движение X является бесконечно малой гомотетией, или гомотетическим движением. если hij = const • 仇 j* ii бесконечно малой ігзометриеп. пли ігзометрическіім движением, если 坛 j = 0 [1].

1.    Проективные преобразования многомерных пространств

Теория групп проективных преобразований псевдоримановых пространств является одним из активно развивающихся разделов дифференциальной геометрии, имеющих приложения в теоретической и математической физике, в теории дифференциальных уравнений и анализе.

Проективные преобразования систематически возникают при исследовании симметрий уравнений математической физики. Достаточно упомянуть, что алгебра Ли инфинитезимальных точечных симметрий уравнения Кортевега-де Фриза является подалгеброй проективной, точнее, аффинной алгебры Ли, а уравнение Риккати можно рассматривать как псвоеобразную реализацию" группы проективных преобразований на прямой [2].

Концепция теории групп была предложена Э. Галуа во время его работы над алгебраическими проблемами. К. Джордан нашел дальнейшее применение теории групп. Теория непрерывных групп была основана Софусом Ли. Исследуя возможность использования расширенных методов Галуа для решения задач, связанных с интегрированием дифференциальных уравнений, Ли обнаружил новый тип групп, которые он назвал непрерывными группами преобразований (в наше время они называются группами Ли).

Впервые задача определения римановых пространств V ^п, допускающих непрерывные группы проективных преобразований, рассматривалась С. Ли и затем учеником Г. Дарбу М. Кёнигсом для случая двумерных поверхностей. Дальнейшее развитие теории проективных преобразований и проективных движений (инфинитезимальных проективных преобразований) в пространствах с линейной связностью связано с именами многих известных математиков - Э. Картан, Л.П. Эйзен-харт, М.С. Кнебельман, И.А. Схоутен, К. Яно, И.П. Егоров, Г. Врэнчану, Ш. Кобаяси и др.

Проблема проективных преобразований в V ^п тесно примыкает к проблеме геодезических отображений псевдориманывых пространств, которая в разное время рассматривалась Е. Бельтрами, У. Дини, Т. Леви-Чивита, Г. Фубини, Л.П. Эйзенхартом, П.А. Широковым. А.З. Петровым, Н.С. Синюковым, А.С. Солодовниковым, В.И. Голиковым, Г.И. Кручковичем, А.В. Аминовой и др. [1].

Как известно, в пространствах постоянной кривизны Sn проективная группа совпадает локально с проективной группой псевдоевклидова пространства, т.е. с группой дробно-линейных подстановок, и зависит от п(п + 2) параметров.

В пространствах Vп непостоянной кривизны порядок проективной группы не превосходит число п(п- 2) + 5 [8], причем в большинстве случаев эта группа состоит из преобразований подобия (гомотетий) или изометрий.

В 1903 г. в пЗаписках Туринской Академии наук11 вышла работа Г. Фубини ПО группах геодезических преобразованийп [9], которая положила начало систематическому определению и изучению пространств с положительно определенными метриками, допускающих проективную группу более широкую, чем группа гомотетий. Позже А. С. Солодовников ( [10], 1956 г.) продолжил исследования Г. Фубини; в трудах Фубини и Солодовникова содержится классификация собственно римановых пространств Vn, п > 3, по (локальным) группам проективных преобразований, более широким, чем группы гомотетий.

Выводы Фубини и Солодовникова опираются на предположение о положительной определенности рассматриваемых метрик. Снятие условия знакоопределенности значительно усложняет задачу и требует принципиально нового подхода к ее решению (см., например, [11-19,33-36]).

В 1987 г. вышла работа А. В. Аминовой [37] (см. также [38]), где в рамках метода подвижного репера была развита техника косонормального репера, которая дала ключ к решению задачи в псевдоримановых пространствах общего вида. В работах А.В. Аминовой [11-19] были найдены все лоренцевы многообразия размерности п > 4, допускающие иегомотетические инфинитезимальные проективные и аффинные преобразования, и для каждого из них - максимальная проективная и аффинная алгебра Ли, включая гомотетическую и изометрическую подалгебры.

Подобная задача для псевдоримановых пространств произвольной сигнатуры ранее не рассматривалась.

Поэтому представленное в данной работе исследование проективно-групповых свойств пятимерных псевдоримановых пространств общей сигнатуры в случае невырожденной характеристики Сегре производной Ли метрического тензора (так называемых жестких ^-пространств) является актуальной задачей, имеющей важное теоретическое и прикладное значение.

2.    Инвариантно-групповые методы в 5-мерных теориях физических полей

В теоретической физике за последние годы значительно возрос интерес к использованию геометрических свойств многомерных, в частности, 5-мерных пространств.

В 1919 г. Т. Калуцей была предложена идея геометризации электромагнитного поля в духе эйнштейновской теории тяготения с помощью увеличения на единицу числа пространственных координат; сейчас в литературе 5-мерная теория называется теорией Калуцы-Клейна. Заслуга Клейна состоит в обобщении линеаризованного варианта теории К ал у цы на общий случай.

В теории Калуцы-Клейна мир описывается 5-мерным псевдоримановым пространственновременным многообразием с квадратичной дифференциальной формой dl2 = 9@户dxadx^     (а, В = 1,…，5).

(2.1)

Пятнадцать компонент 5-мерного метрического тензора определяют десять компонент 4-мерного метрического тензора и четыре компоненты векторного электромагнитного потенциала. Оставшаяся пятнадцатая компонента метрического тензора описывает некоторое скалярное поле.

В качестве уравнений поля используются 5-мерные уравнения Эйнштейна

1        X        с

(2.2)

Rq，b ——2 да.в R + Ag@户=xQa户, где Qdg есть 5-мернніі тензор эііергіш-іімпульса виешиеп материи. Из этих ура.вііеішп стедутот аналоги 4-мерных уравнений Эйнштейна с тензором энергии-импульса электромагнитного поля и уравнения Максвелла. В качестве уравнений движения частиц берутся 5-мерные уравнения гео дезических

d²T ^a         dd d^ ⁷

(2.3)

d/2 =——户7 ~dT~dT где Г駒7 — 5-мерные символы Крпсто(1)(1)еля. Теории с размерное工ъто пространства больше пяти и с полевыми уравнениями, аналогичными уравнениям Эйнштейна, называются теориями типа Кал у цы —— Клейна.

В 1921 году Калуца и Клейн показали, что при определенных условиях (таких как цилин-дричиость ： dgij /дт⁵ = 0, i,j = 1,..., 4) добавление 5-го измерения можс'т объяснить появление электромагнитного поля. Проблема заключается в том, что хотя сама модель является геометрической, условия типа цилиндричности не являются геометрическими. Эта проблема была частично решена Эйнштейном и Бергманом, которые в своей статье 1938 года предположили, что пятое измерение компактифицируется в небольшую окружность S¹, так что в полученном цилиндрическом 5D пространстве-времени R⁴ х S¹ зависимость от т⁵ макроскопически незаметна.

В работе [39] было показано, что если во всех определениях векторов, тензоров и т.д. заменить R4 на R4 х S1 то условия типа тпіліііідрпчііостп станут полиостьто геометрическими.

В работе А.П. Трунева [40] была развита модель фундаментальных взаимодействий на основе теории Кал у цы - Клейна в 5-мерном пространстве.

В работах [41] и [42] рассматривается (4— ( і)-мерііое пространство-время с топологией Т х V³ х V& где V³ ii V^d — однородные ii ігзотропиые подпространства 、 причём V^d (внутреннее подпространство) компактно. Выбран упрощенный сценарий эволюции рассматриваемой модели: задается временная зависимость масштабных факторов подпространств V³ и V^d, приближенно соответствующая полученным ранее решениям уравнений Эйнштейна. На этом фоне исследуются возмущения метрики с одним индексом 4-мерного подпространства Т х V³ и одним индексом внутреннего подпространства V^d. Сжатие масштаба внутретшего пространства (что необходимо для согласования с наблюдениями в настоящее время) приводит к возникновению в 4-мерном физическом пространстве массивных полевых мод рассматриваемых возмущений, которые гипотетически связываются с наличием темной реликтовой материи во Вселенной.

Теорема о соответствии теории Калуцы-Клейна 4-мерной эйнштейновской теории гравитации, взаимодействующей с электромагнетизмом, доказана в [43]. Получено точное решение вакуумных уравнений Эйнштейна в 5-мерном пространстве, представляющее собой решение Боннора 4-мерной теории Эйнштейна-Максвелла. Найденное решение описывает массивный источник, обладающий магнитным и дипольным моментами.

Стабильность вакуумных решений многомерных уравнений Эйнштейна (а значит, сохранение планковских размеров внутреннего пространства) в механизме спонтанной компактификации за счет эффекта Казимира достигается путем чрезмерного увеличения числа полей внешней материи.

Для преодоления этого недостатка в [44] предложено использовать механизм нарушения калибровочных симметрий с помощью петель Вильсона, активно используемый в теории суперструн. Рассмотрена космологическая модель

曲2 =心2 -哈⑴而气--b2(t)(dx5)2 (，,/ = 1,..., 3), содержащая внешние SU(2)-калибровочиые поля и взаимодействующие с ними спиноры. В правой части 5-мерных уравнений Эйнштейна содержится тензор энергии-импульса, соответствующий однопетлевым вакуумным флуктуациям спинорных и калибровочных полей. Полученная из 5-мерных уравнений Эйнштейна система уравнений для параметров @(。и b(。допускает стабильное решение при сравнительно малом числе спинорных полей.

В статье [45] рассматривается 5-мерная космологическая модель с безмассовой 5-пылью в качестве источника. Зависимость от т5 не учитывается, однако феноменологически вводится известный казимировский потенциал. Показано, что уравнения такой модели допускают решение, в котором три пространственных измерения расширяются во времени, а дополнительное измерение стягивается, причем скорость этих процессов определяется количеством 5-пыл и во Вселенной. Строится обобщение на случай произвольного числа тороидальных дополнительных координат. Проводится обсуждение влияния потенциала Казимира на космологические сценарии и возможные его изменения, связанные с наличием во Вселенной тяжелых фермионов.

В статье [46] рассмотрено уравнение геодезических в 5-мерной космологии Калуцы-Клейна. В качестве основного результата декларируется установление на качественном уровне того факта, что 5-скорость и другие величины в рассматриваемом случае будут зависеть не только от времени, но и от массы частицы. При сопоставлении полученных космологических уравнений с 4-мерным и уравнениями в случае материи в виде идеальной жидкости получен аналог метрики Фридмана-Робертсона-Уокера. Приводятся рассуждения о природе и динамике гравитационной постоянной.

В [47], [48] предложена новая интерпретация 5-мерной теории, согласно которой дополнительные слагаемые в 5-мерных вакуумных уравнениях Эйнштейна G^/ = 0 для метрик вида ds2 = e"Cdt2 - e"C(dT2 + dy2 + dz2) - e^^ d-ф2, содержащих произвольные функции 〃(力,3) и “(力,3), отождествляются с правой частью соответствующего 4-мерного уравнения для идеальной жидкости:

G^ = 8ттС[(р - р) 〃 нu” - 」 д>].

Показано, что подобное отождествление приводит к правильным зависимостям давления р и плотности р от времени для некоторой не зависящей от ^ метрики (5-мерная метрика де Леона), являющейся решением уравнений указанного вида, 4-мерный сектор которой соответствует фридмановской модели пространственно-плоской Вселенной, заполненной излучением. Для другой предложенной в этих работах метрики выбором свободного параметра удается добиться соответствия на гиперплоскостях ^ = const с пространственно-плоскими моделями Фридмана как в случае излучения, так и в случае пылевидной материи.

В общей теории относительности четырехмерное пространство-время, наделенное симметриями в форме бесконечно малых преобразований, играет исключительно важную роль.

В своей книге «Пространства Эйнштейна» проф. А.З. Петров дал классификацию четырехмерных пространств-времен на основе их (локальных) групп изометрий, то есть их алгебр Ли векторных полей Киллинга. В работе [79] обсуждались алгебраические и геометрические свойства этих алгебр Ли, были вычислены базисы пятимерных алгебр Ли векторов Киллинга, найденных в книге А.З. Петрова, и рассмотрены приложения.

В пятимериой теории Калуцы-Клейна подробно обсуждается 4。проекция 5。уравнений геодезических. Предложена классификация 5-геодезических, представленных с помощью деформированного 5-конуса. При некоторых предположениях 5D уравнения геодезических дают уравнения движения Лоренца для заряженной частицы. Собственная масса и собственный заряд вводятся как новые параметры частиц; предложены формулы для массы и заряда [80].

Пятимерная общая теория относительности с источниками, которые являются пятимерными точечными частицами или струнами, была исследована в качестве поучительной модели для изучения классических теорий К алуцы-Клейна. В работе [81] получены уравнения поля и уравнения движения пробной частицы, при этом внимание было уделено только тем решениям, которые изо-метричны в дополнительном измерении. Получены выражения для гравитационной и инерционной масс, электрического заряда и скалярной массы. Пробные частицы и источники рассматривались как нити, намотанные на компактное дополнительное измерение; одиночная нить является источником поля, которое является изометрическим или приближенно изометрическим вдоль дополнительного измерения. Предложены некоторые подходы, могущие привести к реалистичной теории Калуцы-Клейна.

В статье [82] рассматриваются векторы Киллинга в пятимерном статическом пространстве. Общие проблемы, касающиеся, в частности, существования и максимального числа векторов Киллинга, изучались в работах по геометрии (см., например, К. Яно [83]).

В физических приложениях векторы Киллинга используются во многих задачах (см., например, А. Коли и Дж. Таппер [84]), включая задачи, связанные с гравитацией.

В [124] доказан факт жесткости для групп, действующих на псевдоримановых многообразиях с сохранением непараметризованных геодезических.

В работе К.М. Буданова и А.Я. Султанова [122] получено каноническое разложение произвольного инфинитезимального аффинного преобразования расслоения Вейля второго порядка над дифференцируемым многообразием со связностью полного лифта. Найдены необходимые и достаточные условия, при которых векторное поле является инфинитезимальным аффинным преобразованием.

В работе А. Фиаловски [125] изучалось пространство модулей всех комплексных 5-мерных алгебр Ли, реализуемое как стратификация по орбифолдам, связанным скачкообразными деформациями. Орбифолды задаются действием конечных групп на простых комплексных многообразиях. Используемый метод определения стратификации основан на построении версальных деформаций алгебр Ли, которые позволяют идентифицировать естественные окрестности элементов в пространстве модулей.

В [126] показано, что подходящее двойное расширение конечномерной неразложимой контактной алгебры Ли снова является контактной алгеброй Ли. В частности, за исключением семейства 5-мерных неразложимых контактно-разрешимых алгебр Ли /5,35, любая 5-мерная неразложимая контактно-разрешимая алгебра Ли может быть получена как двойное расширение 3-мерной алгебры Ли. Семейство /5,35 можно обобщить на семейство (4п + 1)-мериых неразложимых контактноразрешимых алгебр Ли, которые не могут быть получены ни как подвес симплектической алгебры Ли коразмерности 1, ни как двойное расширение контактной подалгебры Ли коразмерности 2.

В работе Л. Галл и Т. Мохаупт [127] разработан формализм, позволяющий систематически строить суперсимметричные теории в зависимости от сигнатур пространства-времени. Используется алгебра суперсимметрии, которая получается путем удвоения спинорного представления, это позволяет обобщить симплектические майорановские спиноры. Для случая, когда спинорное представление является комплексно неприводимым, R-симметрия действует только на внутреннем пространстве. Показано, что возникающие при построении связные группы есть SO(2), SO(1,1), SU (2) ii SU (1 , 1). В качестве приложения построены пре образования суперсимметрии ii суперсимметричные лагранжианы для пятимерных векторных мультиплетов при произвольной сигнатуре «,б). В этом случае группами 足 симметрии являются SU (2) ил и SU (1, 1), в зависимости от того, несет ли спинорное представление кватернионную или паракватернионную структуру. Для евклидовой сигнатуры скалярные и векторные кинетические члены различаются по относительному знаку, что согласуется с известными результатами.

Хорошо известно, что пятимерная теория Калуцы-Клейна обеспечивает геометрическую основу для объединения гравитации и электромагнетизма. Также в этой теории были найдены решения солитонного типа (см., например, Дж. Гросс и Дж. Перри [85]). Вот почему важно исследовать обобщенные векторы Киллиига в 5 。 пространствах.

В работах Ашфак X. Бохари и Асгар Кадир [86] изучался конкретный ряд изометрических векторов Киллинга, полученных из четырехмерного линейного элемента при его определенной параметризации. Аналогичная проблема была решена Крамером Д., Стефани X., МакКаллумом М. [87], и Э. Херлт, Рчеулишвили Г. [88], где для некоторых линейных элементов были получены генераторы групп изометрий в пятимерном пространстве.

В теориях типа Калуцы-Клейна пятимерное пространство выделяется благодаря тому, что из всех многомерных пространств именно в этом пространстве полное многообразие М ⁵ вместе с многообразием типа Калуцы-Клейна М⁴ х S¹ удовлетворяют классическим уравнениям Эйнштейна-Виттена. Отметим, что решение системы уравнений

g* дк 祐 + .阪％ g* + gkj дг^к = Ф.船 для конформных векторов Киллинга приводит к более ясному пониманию природы ограничений на 955 для групп ігзометрип [89].

В [90] было исследовано поведение малых возмущений метрики Калуцы-Клейна в пятимерном пространстве-времени, получены решения уравнений для амплитуды метрических возмущений при условии постоянства возмущений в пятом направлении. Небольшие возмущения отождествляются с гравитационными волнами.

В статье [91] с помощью жордановых матриц была представлена алгебраическая классификация симметрических тензоров второго порядка в пятимерных лоренцевых пространствах типа Калуцы-Клейна. Показано, что возможными типами Сегре являются [1,1111], [2111], [311], [гг111] и их вырождения. Найден набор канонических форм для каждого типа Сегре. Также изучаются возможные непрерывные группы симметрий для каждой канонической формы.

Римановы симметрические пространства имеют следующие два класса пространств в качестве своих естественных обобщений: (А) класс GS-пространств (обобщенно-симметрические римановы пространства), (В) класс GPS-пространств (обобщенные поточечно-симметрические римановы пространства). О. Ковальский [92] показал, что отношение включения (А) С (切 между этими двумя классами является строгим.

В работе [93] утверждается, что в размерности 5 класс (А) и класс (В) должны совпадать.

В работе [94] представлен новый подход к алгебраической классификации симметричных тензоров второго порядка в 5-мерном пространстве-времени. Найдены возможные типы Сегре для симметричного двухвалентного тензора. Получен набор канонических форм для каждого типа Сегре. Также сформулирована теорема, в которой собраны некоторые основные результаты, касающиеся алгебраической структуры тензора Риччи в 5-мерном пространстве-времени.

Существование так называемого «фантомного» скалярного поля в некотором римановом пространстве V4. для которого э ( 1 )( 1 ) ектіівііып теігзор эііер-гіш-іімпульса Т (我) обраттіается в нуль в пятимерной теории Калуцы-Клейна, исследуется с помощью условий интегрируемости соотношений вида Ф 屮;" =кФ 支 Ф 「 + bg^ найденных в [95].

В работе [96] исследованы генераторы групп конформных движений, допускаемых метрикой

曲 ² = 9ii(z) 必 ² — dz² — 933 ( z)d 〃 ² — (дз3(/) sin² “ + 955(2) cos² “ ) d^2-

2955( ， ) cos ^d^d^ — g55(z)d^.

Наличие конформных векторных полей Киллинга позволяет описать законы сохранения для бес-след овых тензорных величин (см. например, Т. Фултон, Ф. Рорлих, Л. Виттен [97]).

Пятимерное риманово многообразие представляет особый интерес в теориях Калуцы-Клейна (см. Э. Виттен [98]). Кроме того, решение обобщенной системы приводит к более глубокому анализу ограничений, которые были наложены на <755 в работе Рчеулишвили Г. [99] при поиске ряда изометрических киллинговых полей.

В работе [100] описывается классификация римановых пространств с пятимерной группой движений с точки зрения решения уравнений Дирака. Идентифицирован класс пространств, в которых уравнение Дирака не допускает полного разделения переменных; точные решения уравнения Дирака получаются в этих пространствах методом некоммутативного интегрирования.

В [101] получена предельная диаграмма для классификации Сегре в 5-мерном пространстве-времени, расширяющая недавнюю работу по пределам тензора энергии-импульса в общей теории относительности. Некоторые результаты Героча [102] о границах пространства-времени в общей теории относительности распространяются на пятимерное пространство-время Ка-луцы-Клейна.

В статье [103] рассматривался метрический тензор однородного изотропного 5-мерного псев-дориманова пространства, разрешающий соответствующие уравнения Эйнштейна в случае, когда пространственная компонента является плоской, сферической или псевдосферической.

Новая 5-мерная классическая единая теория поля типа Калуцы-Клейна формулируется с использованием двух отдельных скалярных полей. Показано, что предложенная процедура решает проблему изменчивости параметра гравитационной связи без требования конформной инвариантности. Соответствующие уравнения поля обсуждаются с учетом возможной индукции градиентов скалярного поля электромагнитными полями.

В работе [104] получен новый предел соответствия, в котором уравнения поля приводят к обычным уравнениям Эйнштейна-Максвелла без условия постоянства скалярного поля.

В [105] геометрическая модель гравитационного взаимодействия с электромагнитным полем в аффинно-метрическом пространстве с кручением и неметричностью представлена как динамика пустого 5-мерного аффинно-метрического пространства. Гравитационное и электромагнитное поля в модели выражаются через метрический тензор 5-мерного пространства-времени. Уравнения теории выводятся из вариационного принципа с использованием формализма (4+1)—расщепления. Получены точные сферически симметричные решения системы полевых уравнений предложенной теории и исследованы их возможные эффекты в астрофизике и физике элементарных частиц.

В статье [106] рассматриваются 5-мерные группы Ли с м ногозначным и функциями Казимира. Показано, что в случае, когда группа Ли состоит из существенно многозначных функций Казимира, пространство орбит коприсоединенного представления является неполу хаусдорфовым, что позволяет сформулировать критерий идентификации этих групп. Полные инволютивные множества функций Казимира извлекаются для всех вещественных пятимерных алгебр Ли, и по этому критерию идентифицируются две алгебры Ли с нехаусдорфовым пространством орбит.

В [107] изучается множество однородных геодезических пятимерных обобщенных симметрических пространств и находятся несколько интересных вариантов поведения геодезических.

В рамках пятимерной теории гравитации рассмотрены пространства, которые допускают семейство максимально симметричных трехмерных подпространств. Для этих пространств строятся пятимерные вакуумные уравнения Эйнштейна и вводится пятимерный аналог массовой функции. Соответствующий ей закон сохранения некоторого заряда приводит к пятимерному аналогу теоремы Биркгофа. Отсюда следует, что для рассматриваемых пространств условие цилиндричности реализуется динамически. Для некоторых полученных метрик условие регулярности приводит к замкнутости пятой координаты. При этом оказывается возможным связать величину периода пятой координаты с сохраняющимся зарядом. Обсуждается проблема разделения динамических степеней свободы скалярного и гравитационного полей, полученных в результате редукции исходного пятимерного действия к четырехмерному виду, и связанная с этим проблема конформной неоднозначности калибровки 4-метрики. Параметризация скалярного поля и 4-метрики, приводящая к конформно-инвариантной теории взаимодействующих скалярного и гравитационного полей, представляется автору статьи наиболее естественной [108].

Последние разработки в теории струн позволяют предположить существование дополнительных пространственных измерений, которые не являются ни малыми, ни компактными. Основой множества космологических моделей бран является та, в которой поля материи ограничены бранным миром, заключенным в пять измерений (объем). Используя основные результаты алгебраической классификации симметричных тензоров второго порядка в 5-мерном пространстве-времени ([91], [94], см. выше), авторы работы [109] представили две теоремы, содержащие некоторые результаты об алгебраической структуре симметричных тензоров второго порядка в 5D Показано, как можно по индукции получить классификацию и канонические формы симметричного тензора второго ранга на n-мер пых ( 几 >  5) пространствах, исходя из классификации в 5D пространствах, представить типы Сегре и соответствующие канонические формы в nD. Эта классификация важна в контексте n-мерных бранных миров. а ， также в рамках 11D супергравитатпш ii 10D теории суперструн.

В работе [НО] изучена структура расслоении Зейферта на односвязных 5-многообразиях. Полученные результаты используются для построения метрик Эйнштейна с положительной кривизной Риччи на указанных многообразиях.

В [111] рассматриваются пятимерные космологические модели в геометрии Лиры с зависящей от времени калибровочной функцией. Получены точные решения пятимерных вакуумных уравнений, обсуждаются их свойства.

В работе [112] проведено исследование некоторых отношений между алгеброй Ли бесконечно малых конформных преобразований касательного расслоения с синектическим лифтом римановой метрики и алгеброй Ли бесконечно малых проективных преобразований.

В работе А. С. Киселева [113] получен ряд решений для пятимерной изотропной космологической модели, построенной на базе ОТО. Материя, заполняющая Вселенную, представлена в виде идеальной жидкости. Показано, что в рамках пятимерной космологии можно объяснить современные наблюдаемые данные о характере эволюции Вселенной. В работе [114] того же автора получены космологические решения в рамках обобщенной теории Калуцы-Клейна для случая пятимерного пространства Римана-—Вейля. Материя в виде идеальной жидкости индуцирует неметричность пространства-времени. Утверждается, что такая теория дает адекватное описание современного этапа эволюции Метагалактики. В рамках пятимерной геометрической теории получен ряд решений для модели, описывающей самогравитирующую идеальную жидкость в пятимерном пространстве с неметричностью типа Вейля [115].

В [116] дан краткий обзор псевдоримановой геометрии пятимерного однородного пространства с конформной группой 。 (4 , 2). Описана топология пространства и обсуждается его связь с конформно компактифицированным пространством Минковского. Описана компактификация с помощью геометрии сферы Ли. Отмечается возможное применение теории START Хайме-Келлера с использованием ее предшественника - 5-оптики Ю.Б. Румера.

В работе [117] исследуются 5-мерные псевдоримановы многообразия, снабженные почти па-раконтактной структурой, которая является аналогом почти контактной структуры в римановой геометрии. Предполагается, что кривизна и аффинор структуры коммутируют. Эти многообразия допускают совместимую косимплектическую структуру в смысле П. Либермана. Найдены явные выражения для связности, кривизны, кривизны Вейля и тензора Риччи. Классифицированы многообразия с контактным потенциалом Риччи и локально плоские многообразия. Описаны все связные односвязные группы Ли, допускающие левоинвариантную структуру. Изучаемые многообразия являются пространствами Уокера - многообразиями с параллельным изотропным распределением, однако классификационная теорема Уокера не применяется.

В работе Й. Микеша [118] пятимерное риманово многообразие М5 с неприводимой SO(3)-структурой рассмотрено в качестве примера абстрактного статистического многообразия. Дока-：заио. что если М5 является статистическим мпогообра：зпем постоянной кріівігзиы. то метрика ри- манова многообразия является метрикой Эйнштейна. Показано, что пятимерная евклидова сфера с неприводимой 5О(3)-структурой не может быть сопряженным симметричным статистическим многообразием. Получены некоторые результаты для пятимерного риманова многообразия с почти интегрируемой 5О(3)-структурой. Доказывается, в част пости, что тензор интегрируемой SO(3)-структуры на пятимерном римановом многообразии является гармоническим симметричным тензором и определяет первый интеграл третьего порядка уравнений геодезических. Рассмотрены некоторые топологические свойства пятимерных компактных и конформно-плоских римановых многообразий с неприводимой 5О(3)-структурой.

В работе [119] методы Т.Т. Думитреску, Г. Фестуччиа и Н. Зейберга [120] обобщены на 5-мерные римановы многообразия М; изучена связь между геометрией в М и числом решений обобщенного спинорного уравнения Киллинга, полученного из 5-мерной супергравитации. Существование одной пары решений связано с почти контактными метрическими структурами. Обсуждается случай М = S¹ х М 4 где М расслоено подмногообразиями со спетпіалыіыми кватертшон-келеровыми свойствами. В случае двух пар решений замыкание подалгебры изометрий, порожденной решениями, требует, чтобы М было S3 ил и Т 3-расслоением на римановой поверхности. Предложена новая суперсимметричная теория для N = 1 векторного мультиплета на К-коитактиом многообразии, допускающая решения спинорного уравнения Киллинга.

В работе Л. С. Ладке, В. К. Джайсвал и Р. А. Хиваркара [121] получены два пятимерных точных решения для пространства-времени типа I Бианки в теории гравитации / (R,T ) в предположении о постоянном параметре замедления и законе вариации параметра Хаббла, соответствующих двум различным космологическим моделям, сингулярной и неособой; для обеих моделей обсуждается их физическое поведение.

В работе [123] исследовался жесткий предел 5 。 конформной супергравитации с минимальной суперсимметрией на римановых многообразиях. Необходимым и достаточным условием существования решения является существование конформного вектора Киллинга. Обсуждается, при каких обстоятельствах допускается кинетический член Янга-Миллса в действии векторного мультиплета.

Работы авторов ( [24]- [31]) посвящены решению задачи определения всех 5-мерных жестких ^-пространств А» т.е. псевдоримановых многообразий (М⁵,д) произвольной сигнатуры с (невырожденной) характеристикой Сегре х = { 『 i , •••,『 “} ,『 1 , •••,『 “ Е N, ri + ... + г^ = 5 , и вещественными собственными значениями производной Ли ^х9 метрики g в направлении инфинитезимального преобразования X, допускающих (иегомотетические) проективные и аффинные движения (т.е. инфинитезимальные проективные и аффинные преобразования), и для каждого из них - определение структуры соответствующих максимальных проективной и аффинной алгебр Ли, включая классификацию ^-пространств "221 типа {221} по максимальным алгебрам Ли проективных и аффинных преобразований, более широким, чем алгебры Ли гомотетий.

Решение этой задачи основано на разбиении пространств (М5, g) по типам в соответствии с алгебраической структурой билинейной формы 九 = Lx g и включает несколько этапов ( [128][131]). В итоге получены следующие основные результаты:

Полностью решена задача определения 5-мерных жестких ^-пространств "» т. е. 5-мерных псевдоримановых пространств (М5,g), допускающих нетривиалыіые решения 九=соnst • g уравнения Эйзеихарта с вещественной невырожденной характеристикой Сегре %. Для каждого из найденных ^-пространств получены о6ш,не решения уравнения Эігзенхарта： каждому решешпо отвечает квадратичный первый интеграл уравнений геодезических. Найдены формы связности и кривизны 5-мерных пространств Нх. Получены необходимые и достаточные условия постоянства кривизны жестких һ-пространств. Описаны свойства определяющих функций проективных движений и ковариантно постоянных симметричных тензоров в жестких һ-пространствах. Установлены необходимые и достаточные условия существования в 5-мерном пространстве негомотетического проективного движения заданного типа %. Показано, что аффинная алгебра Ли в жестком 九- пространстве непостоянной кривизны состоит, самое большее, из гомотетий. Доказано, что если 5-мерное жесткое ^-пространство допускает иегомотетическую проективную алгебру Ли 4, то эта алгебра содержит подалгебру Hr-i инфинитезимальных гомотетий размерности г - 1.

3.    Классификация 九-пространств типа {221} по алгебрам Ли проективных и аффинных движений

В работе [32] дана классификация ^-пространств "221 непостоянной кривизны по (иегомоте-тическим) алгебрам Ли инфинитезимальных проективных и аффинных преобразований; перечислены все проективно-подвижные ^-метрики типа {221} и указаны размерности, базисные элементы и структурные уравнения действующих в них максимальных проективных алгебр Ли. Доказана следующая теорема.

Теорема 1 Если 5-мерное һ-пространство "221 mu na { 221 } непостоянной кривизны:

g = 61(/2 — /і)2(/з — /і) (2Adx1dx2 - А² ( ²    +     ¹      (ch;²)²) +

J2 ^-/і    ./3 ^-/1/

6 2 ( / i - /2 ) 2(/з - /2) (2Bd_x3 d;⁴ -炉( -Д- +         (d ， ⁴)] +

J1 - J2   J3 -/2/       /

⁶3^(/1 ^- / з ^{) 2 ( /} 2 ^- /3^)2(d;5)2,

夕=/і + /2 + (1/2)/з, где /і = £і,2 + (1 -£і)сі, /2 = £2,4 + (1 -£2^2, /з = 〃(，5), Q, С2-const, А =印(；1 + 丁(；2)) + 1 -印， B = £2 (，3 + ®(，4)) + 1 — £2； £і, £2 принимают независимо значения 0 или 1, 61,62,63 = ±1, 丁 —функция ,2, ® — функция ,4, допускает негомотетическое проективное движение, то это пространство и действующая в нем максимальная проективная алгебра Ли Р определяются указанными далее формулами, где 石 一неаффинное проективное движение,石 一неизометрическая инфинитезимальная гомотетия,石 一инфинитезимальная изометрия.

I . Н-пространства " 221,1 непостоянной кривизны ( £ 1 = £ 2 = 1, / 3² + 丁 ‘2 + сУ² = 0).

• I . A . Функции / з ，丁 и с являются решениями уравнений

  /3 _ Q + b /2 + b/з + с

(( ， ²)² + b ， ² + e) 丁" + 3(;² - q + b) 7 ‘ = 0,

((;4)2 + b,4 + e) J'+ 3(;4 - q + b) J = 0, где Q,b,e — постоянные, связанные условием q — b(e — b) = 0; /3 = 0. Размерность проективной алгебры, Ли dimP = 1. Алгебра Р ііАі/тяні/т(і на проективііое ск^кторное поле e1 = {(3q — 2b — ;2)(;1 + 7) - (,22 + b,2 + e) 7 '}% + (,22 + b,2 + e)%+

{ (3q - 2b — ,⁴)(,³ + e) - (,4² + b,⁴ + e" } d3 + ( ， 42 + b,⁴ + e)d4 + /³ +:/³ + ^С %.

/3

• I . B .    Фуіі/ки^ш / 3 , ^т 〃® илшот вид

Со     G     Q

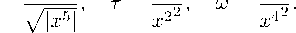
При Со = 0 (/3 = 0 丿 размерность прссктизн (心 алгебры, Ли dim Р = 2. базис в Р вклю^іает проективное векторное поле

B 1 = - ;²(;¹ + 7 )& + ,22% - ,⁴(,³ + ⑴川 3 + ,4². - 2,5/385

и инфинитезимальную изометрию

Е 2 = — 2/1di + т²% — 2т3дз + £4^4 — 2x535.

Структурное уравнение имеет вид

• [Е 2 ,Е і ]    = Е і .

При /з = 0 добавляе. тся тра hcaxrilx Е з = 85. В .力 〃 а к с л t рше dim Р = 3. Р 〃 а а lant/ а ? а ，力 а ♦                                                 и

Е i (/ з = 0). Е2 ” Ез- 〃川.〉"〃 м [Е і ,Е з ] = 0, [Е2, Е3] = 2Е3. к           и и

• I .C. ◎/〃?,"〃& 丁 &  G /ada? 。机 с 忍 расе 〃 с7 〃 бами

3а/Ь

7 = a

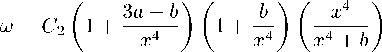
3а/Ь

/ з = 0.

Размерность проективной алгебры Ли dim Р = 2. Базис в Р состоит из проективного движения

Е i = { (3q — 2b — x²)(x1 + 丁 ) — x² (x² + b) 丁 ‘ } di + x²(x² + b)%+ n

{ (3q — 2b — x⁴)(x³ + g) — x⁴(x⁴ + b) 〃} дз + x⁴(x⁴ + b)d4 + (3q — 2b)x⁵d5.

и піраіісляіі^и-и Е 2 = д^: [Е2, Е1] = (3q — 2b)Е2. и

• II . H-пространства "221,2 непостоянной кривизны ( £1 = 1, £2 = 0, /2 = С2 = const, /32+ 丁 ‘2 = 0).

• II . A . He no с!поянн ( ія ф у 〃如罔 ия / 3 з ( и)ается і/равнени е.м

• / з’’ _ 3         / з + 。

=

/3²    2 /2 + 3а(/з — C2) — с2

Е i = {— x²(x¹ + т) — (x² + 3а + C2)(x² — с?)т ‘ } di + (x² + 3а + cz)(x² — С2 )% —

( C2x³ + x⁴)d3 + (3а + C2)x⁴d4 + ^{( / з + 3 a +} ， ^{( / з} ^2) %

/3

и дв e 机 pa 〃 сляи.ии Е 2 = дз, Е з = 84. Сп %рt/ 汇〃 z? /рны е t /равнения: и       и

[Е і ,Е 2 ] = С2Е2, [Е і ,Е з ] = Е 2 — (3а + с ? )Е з , [Е 2 ,Е з ] = 0.

• II .B. Постоянна,я фі/нкі^ия /3 = 0.

  т = G

  
  

  (1+Т2 )(1 - и ) ^1+а/С2,

  
  

где а = const. Размерность проектиспіой алгебры Ли dim Р = 4. Ба^іи: в Р вклю^іает проективное векторное поле

Е i = { (а + 2c2 — x²)(x¹ + т) — x²(x² — C2 )т ‘ } ді + x²(x² — С2 )82+

((а + C2)x³ — x⁴)d3 + (а + 2c2)x⁴d4 + (а + 2c2)x5d5

и три трансляции Е 2 = дз, Е з = &  и Е 4 = 为， и       и        и

[Е2,Еі] = (а + С2)Е2, [Ез,Еі] = -Е2 + (а + 2с2)Ез, [Е4,Еі] = (а + 2с2)Е4, остальные скобки Ли равны нулю.

• III . Н-пространства Н221,3 непостоянно 位 кривизны 但 1 = £2 = 0, А = В = 1, /1 = ci а /2 = С2 — постоянные, /3 = const).

Фі/и/кі^ия /з является реіиениелі і/р ( івнешія

/3' _ 2 /з — ^c1 — ^c2 — ^а

/32 = (/з-С1)(/з-С2), где а — пос!поянн(ія. Размерное"іъ проективной алгебры Ли dimP = 5. Алгебра Ли Р 〃〃机闵〃？〃〃а 外а проективное движение

Е i = ((3а + ci + 2c2 ) ^1 - ^²)di + (3а + 2ci + С2 ) ^²д2+

((3а + 2ci + C2 ) ^³ — т⁴)дз + (3а + ci + 2c2 ) £⁴?4 + ——— "|‘ 『 ³ ---C2185

/з u пять трансляций Е2 = di, Ез = 82, Е4 = дз u Е5 = 84. и       и       и        и

Структурные уравнения алгебры Ли Р имеют вид

[Е2,Е1] = (3а + ci + 2с 2 ) Е 2 ,   [Е3, Е]] = —Е2 + (3а + 2ci + С2 ) Ез,

[Е4, Еі] = (3а + 2ci + c2)Е4,   [Е5, Еi] = — Е4 + (3а + ci + 2c2)Е5, остальные скобки Ли равны нулю.

Заключение

Статья носит обзорный характер по теме ^пИнвариантно-групповые методы в пятимерной теории физических пол ей^п, что объясняет обширный список литературы. Появление подобного обзора, заполняющего известный пробел, стало необходимым. Идя навстречу пожеланиям рецензента, мы расширили часть обзора, касающуюся полученных авторами этой статьи результатов, описывающих симметрии пятимерных искривленных пространств в форме проективных движений, сохраняющих геодезические. В частности, исследованы 5-мерные жесткие ^-пространства Н221, Н32, Н41 ii Н5. т.е. псевдоримаиовы мтюгообравня (М⁵,g) проігзволыюп сигнатуры с (невырожденной) характеристикой Сегре х = { 『 1 ,...,『 左 } ,『 1 ,...,『 左 Е N, ri + ... + г ^ = 5 , и вещественными собственными значениями производной Ли Lx g метрики g в направлении инфинитезимального преобразования X, допускающие инфинитезимальные проективные и аффинные преобразования. Для каждого из них определены структуры соответствующих максимальных проективной и аффинной алгебр Ли, включая классификацию ^-пространств Н221 типа {221} по максимальным алгебрам Ли проективных и аффинных преобразований, более широким, чем алгебры Ли гомотетий. Доказательства утверждений можно найти в цитированной литературе.