Прогноз риска развития опухоли с учетом регуляторных механизмов организма человека и процесса ангиогенеза

В последние десятилетия противодействие смертности от онкологических заболеваний в развитых странах стало одним из приоритетов в сфере медицины и биомедицинских исследований [1, 2]. Изучение воздействия негативных факторов среды обитания и образа жизни на возникновение раковых опухолей является неотъемлемой частью онкологических исследований. Это направление науки имеет огромное значение в свете все возрастающего числа случаев раковых заболеваний по всему миру. Негативные факторы среды и образа жизни могут значительно увеличивать риск возникновения рака, и поэтому изучение их воздействия имеет важное практическое значение для создания эффективных стратегий по предотвращению и лечению рака.

Научные исследования показывают, что загрязнение окружающей среды токсичными веществами, тяжелыми металлами и прочими химическими соединениями может значительно увеличить риск развития рака у людей. К одному из таких факторов можно отнести алюминий, широко используемый

Чигвинцев Владимир Михайлович – кандидат физико-математических наук, научный сотрудник отдела математического моделирования систем и процессов (e-mail: ; тел.: 8 (342) 237-18-04; ORCID: .

металл в различных отраслях промышленности, который попадает в окружающую среду через производственные процессы, утилизацию отходов и продукты повседневного использования. В частности, исследователи рассматривают потенциальную роль алюминия в модуляции молекулярных путей, участвующих в прогрессировании рака толстой кишки, таких как эпителиально-мезенхимальный переход и апоптоз [3]. В исследованиях сообщалось о способности биоаккумуляции алюминия потенциально индуцировать канцерогенез молочной железы, вызывая нестабильность генома [4].

Негативные факторы среды обитания и образа жизни оказывают существенное влияние на возникновение раковых опухолей как напрямую, так и опосредованно – через снижение функциональности защитных механизмов организма. Нарастание уровня алюминия в организме человека приводит к нарушениям структуры и функции костной и нервной тканей, репродуктивной системы, системы кроветворения, а также в системе иммунного ответа.

Одним из ключевых аспектов изучения воздействия негативных факторов на развитие рака является определение механизмов, через которые эти факторы воздействуют на клетки организма и организм в целом и вызывают изменения, приводящие к развитию опухолей. Это включает в себя изучение генетических аспектов, эпигенетических механизмов, влияния окружающей среды на метаболические процессы и др.

Техногенные факторы среды обитания могут привести к патоморфозу, ухудшить течение и исход онкологического заболевания [5]. Испытывают влияние указанных факторов и регуляторные (иммунная и нейроэндокринная) системы; проведенные исследования показывают, что техногенные химические факторы оказывают негативное воздействие на функционирование данных систем [6–8].

Иммунитет играет определяющую роль в процессах развития новообразования. В организме человека в течение его жизнедеятельности возникают аномальные клетки, которые в ходе дальнейшего роста могут образовывать раковые опухоли, но благодаря работе иммунной системы в большинстве случаев они прекращают свой рост. Показано, что функциональные нарушения иммунной системы являются одной из главных причин высокого уровня заболеваемости злокачественными новообразованиями [9, 10].

В экспериментах in vitro и in vivo трудно понять взаимосвязь между влияющими факторами, поэтому сложно объяснить механизм онкогенеза с учетом взаимодействия элементов иммунитета при изменении поступления питательных веществ за счет ангиогенеза. Применение методов математического моделирования позволяет исследовать как внутренние связи различных элементов, так и взаимодействия между элементами системы в целом [11–13]. Основная проблема математического моде- лирования роста опухоли с учетом ангиогенеза заключается в многомасштабности и многофакторности этого процесса.

Целью исследования является оценка риска развития раковой опухоли с использованием прогностической математической модели для описания динамики аномальных клеток ткани с учетом влияния механизмов ангиогенеза и реакции иммунной системы в условиях воздействия химических факторов среды обитания.

Материалы и методы. Динамика прогрессирования опухоли обусловлена результатами соперничества между субпопуляциями за доступ к глюкозе, которая является ключевым источником энергии и основным строительным материалом опухолевых клеток. В контексте механизмов защиты организма от неконтролируемого роста аномальных клеток рассматривается воздействие комплекса элементов иммунной системы с учетом регулирующего влияния эндокринной системы. В качестве основных характеристик клеток, существенных для описания механизмов образования опухолей, выделяются скорость деления, продолжительность жизни клеток, максимальная плотность образуемой ткани, антигенность и уровень потребления глюкозы.

Из-за сложности процессов иммунного ответа, учитывая нейроэндокринную регуляцию, в работе используется ряд гипотез и предположений. Одной из основных гипотез является идея о равномерном распределении клеточных популяций в представительной области ткани органа в любой момент времени [14]. Кроме того, предполагается, что изменения любой переменной модели зависят от текущих значений всех переменных, что означает, что последние содержат информацию об истории процесса.

Принимается предположение о регуляции иммунного ответа сигнальными белками, находящимися в трех основных тканевых объемах: головном мозге (гипофизе, гипоталамусе), брюшной полости (надпочечниках) и в органе-мишени. Взаимодействие между пространственно удаленными органами учитывается с помощью введения временного запаздывания. Регуляторное воздействие иммунной и нейроэндокринной систем имеет отсроченный характер, поскольку требуется время на передачу сигналов от органов-источников к целевому органу.

Защитные механизмы активируются после контакта макрофагов и опухолевых клеток, порожденных мутацией нормальных клеток. Процесс устранения аномальных мутировавших клеток сопровождается синтезом информационных молекул, таких как цитокин интерлейкин-1 [15].

Изменение уровня интерлейкина-1 приводит к изменению скорости образования интерлейкина-2 Т-хелперами, что вызывает изменения в скорости синтеза гормона кортиколиберина путем воздействия на гипоталамус. Кортиколиберин воздействует на переднюю долю гипофиза, что приводит к изме- нению скорости секреции адренокортикотропного гормона (АКТГ). АКТГ, циркулируя в крови, в свою очередь, влияет на активность надпочечников, регулируя выделение кортизола. Изменение уровня кортизола вызывает обратную реакцию в секреции АКТГ и интерлейкина-1 [16].

Интерлейкин-2 оказывает стимулирующее воздействие на процесс производства NK-клеток [17], цитотоксических T-лимфоцитов [18] и В-клеток [19, 20]. NK-клетки производятся костным мозгом и осуществляют механизм уничтожения аномальных клеток в начальной стадии иммунной борьбы с раковыми образованиями. NK-клетки неспецифичны по отношению к аномальным клеткам, и для их работы используется механизм распознавания «свой – чужой».

Большая часть возникающих аномальных клеток подвергается нейтрализации на начальной стадии защиты организма без активации специфического иммунного ответа. В разрабатываемой модели учтено подавляющее воздействие кортизола [21, 22] и стимулирующее влияние интерлейкина-2 на интенсивность производства NK-клеток [23]. Специфический адаптивный иммунитет в основном связан с производством антител В-клетками, которые блокируют жизнедеятельность аномальных клеток, а также с уничтожением аномальных клеток цитотоксическими T-лимфоцитами [23, 24]. Указанные иммунные клетки начинают активное размножение после получения сигнала о наличии популяции аномальных клеток за счет стимулирующего влияния интерлейкина-2. Когда специфические клетки достигают определенной численности, начинается производство антител В-клетками [25] и выход цитотоксических Т-лимфоцитов в кровеносную и лимфатическую системы. Способность иммунных клеток бороться с аномальными клетками подавляется кортизолом [26]. Наличие постоянного стрессора (кортизола) приводит к снижению активности натуральных киллеров, замедлению размножения Т-лим- фоцитов, предназначенных для уничтожения аномальных клеток, и препятствует нормальному производству антител.

Система кровеносных сосудов играет основную роль для поступления питательных веществ (углеводов), необходимых для поддержания жизнедеятельности всех тканей в организме человека. В результате ангиогенеза происходит формирование новых сосудов, которые постепенно распространяются, создавая новую местную кровеносную систему. В онкологической медицине активно исследуется использование антиангиогенной терапии [27, 28], которая приводит к уменьшению поступления питательных веществ в опухоль и замедлению ее роста. Недавние исследования показывают, что на процесс ангиогенеза могут влиять различные факторы [29], приводя к структурным изменениям сети кровеносных сосудов.

Поступление питания от артериол к клеткам происходит за счет диффузии питательных веществ сквозь межклеточное пространство. При недостатке питательных веществ клетки органа начинают выделять фактор роста эндотелия сосудов (VEGF), который стимулирует рост капилляров от артериол [30, 31]. Наличие капилляров в ткани значительно увеличивает ее проницаемость для питательных веществ и позволяет восполнить недостаток. В модели рост капилляров описывается за счет локального изменения пористости ткани.

Графическое представление, отображающее основные взаимосвязи между переменными модели, включает комплекс взаимосвязанных элементов иммунной, нейроэндокринной систем и клеток органа, составляющих систему кровеносных сосудов, приведено на рис. 1.

Исходя из представленной выше схемы взаимодействия, математическую модель можно представить в виде системы из 19 обыкновенных дифференциальных уравнений первого порядка с запаздывающим аргументом.

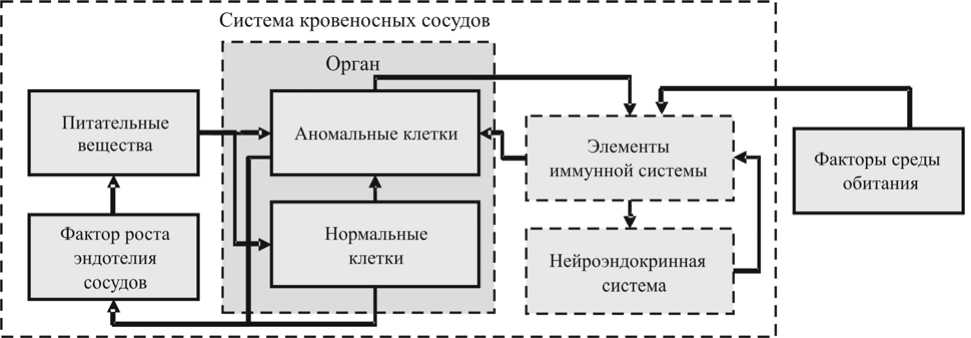
Рис. 1. Схема функционирования иммунной и нейроэндокринной систем при развитии раковой опухоли

Для описания изменения концентрации аномальных клеток с учетом иммунной регуляции используется следующее уравнение, при этом учитывается параметр антигенности, их видимость для различных клеток иммунитета (коэффициенты уравнений определяются при идентификации модели с использованием данных экспериментов in vivo и / или in vitro ):

■ = kmC + C m 'll 1--— I dt c c      k2m + pJ

• -    k з С т С м Н ( S^m - k 4 ) -

• -    k 5 C A C m H ( S m - k 6 ) - k m C m -

• -    k,c_NKc m 1 1 - k₉ CK ⁽ t~ T\ I H(S m - k ₁₀) -

• 8 NK c (     9 1 + CK (t - T) J V 10;

• - k_uC_CTLCm 1 1 - k₁₂   CK ⁽ t ~ T ). I H(S^m - k ₁₃) -

• 11 CTL c (     121 + CK (t - T) J   v 13;

Nm

14 CpCp, где ρ – совокупная плотность клеток органа, кле-ток/мл;

C _c ^m – концентрация аномальных клеток органа в окрестности расчетной точки, клеток/мл;

S^m – видимость для элементов иммунной системы (антигенность) аномальных клеток органа (нулевое значение соответствует характеристике нормальной клетки), б/р;

C M – концентрация макрофагов (моноцитов), клеток/мл;

C A – концентрация антител, мМЕ/мл;

C NK – концентрация NK-клеток (естественные киллеры), клеток/мл;

C K – концентрация кортизола, нанограмм/мл;

C_CTL – концентрация цитотоксических Т-лимфоцитов, клеток/мл;

C_P – концентрация питательных веществ, мг/мл.

Для описания образования новых аномальных клеток используется первое слагаемое. При этом для установления верхней границы деления аномальных клеток вводится дополнительная характеристика – максимальная плотность образуемой ткани. Второе слагаемое описывает уничтожение аномальных клеток макрофагами, при этом выделяется сигнальный белок интерлейкин-1. Для описания процесса нейтрализации аномальных клеток специфическими антителами используется третье слагаемое.

Четвертое слагаемое характеризует естественную смерть аномальных клеток, значение коэффициента определяется из значения продолжительности жизни аномальной клетки. Пятое слагаемое представляет собой описание уничтожения аномальных клеток органа-мишени при помощи NK-клеток. Уничтожение происходит при контакте инфицированной клетки с NK-клеткой. Кортизол оказывает подавляющее воздействие на активность NK- клеток, и его воздействие имеет запаздывающий характер из-за времени, необходимого для доставки из надпочечников к органу-мишени.

Для описания уничтожения аномальных клеток цитотоксическими Т-лимфоцитами используется шестое слагаемое в правой части уравнения. Уничтожение происходит после контакта аномальной клетки с цитотоксическим Т-лимфоцитом. Кортизол также оказывает угнетающее действие на работу цитотоксических Т-лимфоцитов. Для описания эффекта накопления данного типа клеток в лимфатических узлах до достижения определенного уровня используется функция Хевисайда. Последнее слагаемое описывает смерть аномальных клеток при недостатке питательных веществ.

Описание изменения иммунологических и нейроэндокринных элементов выполнено с помощью балансовых уравнений вида:

dC^ = Vk+ c -Yk- C - , (2) dt ix,iy,i jx,jy,j, где kX+iCyi - слагаемое, описывающее увеличение скорости изменения концентрации показателя Cx за счет воздействия влияющих факторов Cy,i;

k-Cyj - слагаемое, описывающее уменьше- ние скорости изменения концентрации показателя Cx за счет воздействия влияющих факторов Cy,i.

Вид уравнений (2) и значения их параметров приведены в статье, описывающей рост опухоли с учетом регуляторных систем [32].

Для описания изменения концентрации питательных веществ используется следующее уравнение, соотношение учитывает уменьшение концентрации за счет поглощения питательных веществ аномальными и здоровыми клетками:

dCP dt

m я 15 V^C    Л-16 V^ST ,

где C_ST – концентрация здоровых клеток органа, клеток/мл;

C _c ^m – концентрация аномальных клеток органов в окрестности расчетной точки, клеток/мл.

Изменение концентрации фактора роста эндотелия сосудов (VEGF) описывается соотношением, учитывающим выработку белка аномальными и здоровыми клетками органа при недостатке питательных веществ, а также механизм естественного клиренса:

^dC VEGF dt

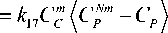
N

18 ST P P 19 VEGF ^,

где C_c^m – концентрация аномальных клеток органов в окрестности расчетной точки, клеток/мл;

C_ST – концентрация здоровых клеток органа, клеток/мл;

C_p – концентрация питательных веществ, мг/мл; N

C_p – граничная концентрация питательных веществ необходимых для поддержания жизнедеятельности клеток, мг/мл.

Изменение пористости ткани, моделирующее рост капилляров под действием фактора роста эндотелия, характеризуется следующим уравнением: соотношение описывает стимуляцию роста фактором роста эндотелия сосудов и естественную деградацию сети капилляров:

dt   k 20 C VEGF   ^k 21 , D >  D N ,

где C _VEGF – концентрация фактора роста эндотелия сосудов VEGF, МЕ/мл;

D – пористость ткани, связанная с наличием капилляров в ткани и тканевой жидкостью, б/р;

D _N – пористость ткани, выше которой можно говорить о наличии капиллярной сети, и которая может послужить началом роста новых капилляров, б/р;

D – пористость ткани в окрестности расчетной точки, б/р.

Скорость изменения концентрации аномальных клеток, обусловленная делением, в произвольной точке органа можно описать диффузионным уравнением следующего вида, основное направление роста ориентировано на область с наименьшей плотностью ткани:

dСCm dt

,~ d

= - k^D,

где C_c^m – концентрация аномальных клеток органа в окрестности расчетной точки, клеток/мл.

Диффузия глюкозы в ткани описывается следующим дифференциальным уравнением в частных производных, при описании учитываются механизмы перемещения при растворении в тканевой жидкости и с помощью капиллярной сети:

dСP dt

5 C

= - k 23 D— ^p- , d x

где C P – концентрация питательных веществ, мг/мл.

Факторы роста эндотелия сосудов имеют тенденцию диффундировать от области с более высокой концентрацией к области с более низкой концентрацией. Проницаемость тканей играет важную роль в диффузии VEGF. Диффузия концентрации факторов роста эндотелия сосудов определяется следующим уравнением, описывающим движение белка VEGF от клеток с недостаточным питанием до стенок капилляров с целью стимуляции их роста:

^dC VEGF = Ъ ГХ ^{d C} VEGF dt         ²⁴     d x   ’

где C _VEGF – концентрация фактора роста эндотелия сосудов VEGF, МЕ/мл.

Идентификация модели выполнена с использованием имеющихся в литературе экспериментальных данных, полученных при исследовании процесса возникновения и роста аномальных клеток в тканях почек, значения параметров модели приведены в таблице.

Параметры математической модели динамики роста аномальных клеток ткани с учетом влияния механизмов ангиогенеза и реакции иммунной системы

Параметр	Значение	Источник
k 1	2,35·10–11 (1/клеток·день)	[33]
k 2	1,2·107 (клеток/мл)	–
k 3	10–14 (мл/клеток·день)	–
k 4	0,85 (б/р)	–
k5	8,6·10–10 (мл/мМЕ·день)	[34]
k 6	0,7 (б/р)	–
k 7	0,0043 (1/клеток·день)	[35]
k 8	2,5·10–17 (мл/клеток·день)	[36]
k9	0,5 (б/р)	–
k10	0,5 (б/р)	–
k11	6,6·10–18 (мл/клеток·день)	[36]
k 12	0,5 (б/р)	–
k 13	0,8 (б/р)	–
k 14	0,046 (мл·клеток/мг·день)	[37]
k15	3,6·10-3 (мг/клеток·день)	[37]
k 16	1,5·10-3 (мг/клеток·день)	[37]
k 17	8,3·10-7 (мл·МЕ/клеток·мг·день)	[38]
k 18	6,5·10-7 (мл·МЕ/клеток·мг·день)	[38]
k 19	0,0019 (1/день)	[38]
k20	0,0135 (мл/МЕ·день)	[38]
k 21	7,13·10-3 (1/день)	[38]
k22	0,02 (мм/день)	–
k 23	0,83 (мм/день)	–
k24	1,2 (мм/день)	[39]

Для использования модели при описании онкогенеза в других органах необходимо определить значения указанных коэффициентов на основе эмпирических данных, отражающих специфику клеток данного органа.

Взаимодействие между популяциями клеток и информационными молекулами организма основано на клонально-селективной теории, законе действующих масс, а также использовании характеристик взаимодействия и марковских процессов рождения и гибели.

Нарушения функционального состояния иммунной системы рассматриваются на примере производящего иммунные элементы костного мозга, изменения в работе которого происходят в связи с химической контаминацией алюминием.

Изменение функциональности костного мозга влияет на скорость продукции различных клеток врожденного и приобретенного иммунитета, что впоследствии приводит как к количественным (изменение количества иммунных и вспомогательных клеток иммунной системы), так и качественным изменениям в состоянии иммунитета (снижение функциональной активности). Эволюция функциональных нарушений иммунной системы описывается уравнением, исходя из принятой гипотезы об аддитивности скоростей изменения функциональности систем от химических факторов, и записывается следующим образом:

dF lx \

— = aF + bl -1, (9) dt xN где a – коэффициент, отражающий скорость роста нарушения функциональности иммунной системы F за счет естественных механизмов, 1/год;

b – коэффициент, описывающий интенсивность воздействия негативного фактора (алюминия) на нарушение иммунной системы F , 1/год;

x – доза алюминия, поступающего в организм человека;

x^N – нормативное (предельно допустимое) значение негативного фактора (алюминия);

x – скобки Маколея (Macaulay brackets): (X^х) = max( x ,0).

Уравнение (9) дает возможность приближенного описания эволюции функциональных нарушений и учитывает процессы макроуровня – естественное старение, восстановление, накопление нарушений продуцирующей функции за счет ненормативных потоков веществ. Пример использования эволюционного подхода для учета влияния оксида алюминия на накопление функциональных нарушений иммунной системы приведен в статьях [40, 41].

Для решения поставленной задачи Коши используется неявный численный метод Рунге – Кутты третьего порядка (РадоIIА); данный алгоритм принадлежит к группе алгоритмов, используемых для решения жестких систем дифференциальных уравнений с запаздывающим аргументом. Так как скоростные характеристики изменения описываемых показателей отличаются порядком величин, для оптимизации процесс расчета разбит на три разновременных этапа в порядке увеличения скоростных характеристик: эволюция системы кровеносных сосудов, возникновение новых аномальных клеток, процесс регуляции иммунной и нейроэндокринной систем. Область моделирования была разбита на 1000 × 1000 ячеек.

Численное моделирование проведено в двумерной постановке на тестовом образце почечной ткани. Почки являются одним из органов накопления алюминия, после костной и нервной ткани, и основным – для выведения его из организма. Алюминий повреждает не только структуры клеток, но и сами клетки, обладая прямой цитотоксичностью, вызывая некроз эпителиальных клеток почечных канальцев. Снижение выделительной функции почек ведет к увеличению концентраций алюминия в организме и усилению его негативного влияния на иммунную систему.

Для количественной оценки риска развития раковой опухоли используется метод Монте-Карло. Для выбранных значений функциональной поврежденно-сти иммунной системы проведена серия численных расчетов, в ходе которых случайным образом задавались следующие параметры, характеризующие свойства аномальных клеток: скорость деления, время жизни, максимальная плотность образуемой ткани, антигенность и потребление глюкозы.

Результаты и их обсуждение. Динамика изменения численности аномальных клеток во многом определяется случайным процессом возникновения и свойствами образовавшихся в результате мутации аномальных клеток. Из анализа результатов проведенных исследований следует, что процесс развития может протекать по различным сценариям. Представленная модель позволяет описать динамику различного типа онкогенеза с учетом ангиогенеза, например, опухоли с различной скоростной характеристикой деления аномальных клеток. На рис. 2 показана динамика изменения концентрации раковых клеток при «солидном» виде опухоли с низкой скоростью деления аномальных клеток.

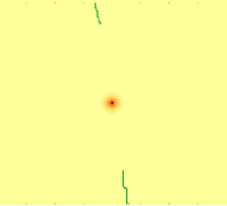
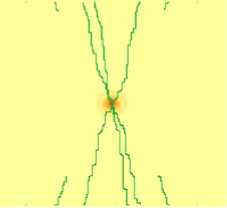
46-й день

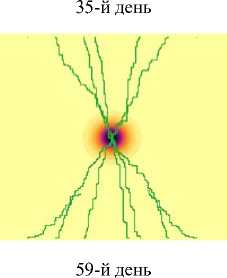
Рис. 2. Динамика роста «солидной» опухоли с низким параметром скорости деления

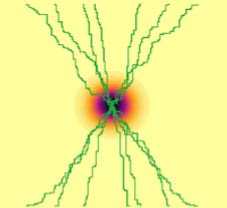
91-й день

Модель позволяет учитывать особенности ангиогенеза при быстром росте опухоли. В данном случае из-за значительного недостатка питательных веществ происходит значительное выделение белка роста, что ведет к хаотическому росту сосудов. Результаты моделирования для «солидной» быстрорастущей опухоли представлены на рис. 3.

Модель позволяет также исследовать особенности динамики роста опухоли с учетом различной функциональности иммунной системы. На рис. 4 и 5

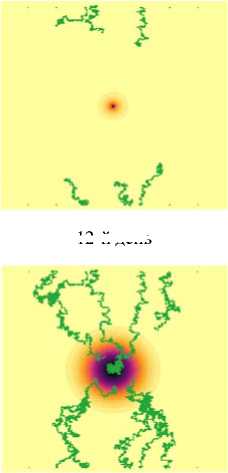
12-й день

20-й день

Рис. 3. Динамика роста «солидной» опухоли с высоким параметром скорости деления

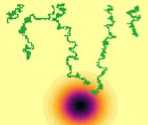
15-й день

25-й день

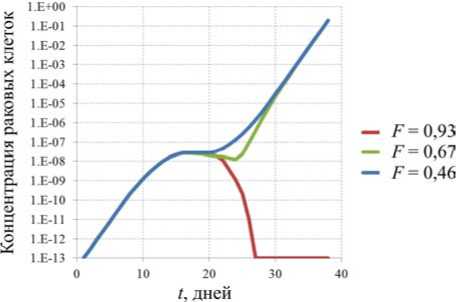
Рис. 4. Динамика роста опухоли с высоким параметром

представлены результаты расчетов роста быстрой и медленной опухоли с учетом различной функциональности иммунной системы. Функциональность для сценарного расчета определялась из решения эволюционного уравнения (формула (9)), рассматривался срез значений функциональности в возрасте 40 лет при различной пожизненной экспозиции алюминием. При суточной дозе 0,4 мг/кг в сутки функциональность иммунной системы составила F = 0,93. Функциональность F = 0,67 и F = 0,46 достигается при дозе 4 и 40 мг/кг в сутки соответственно.

Исходя из полученных результатов, при минимальном повреждении иммунной системы F = 0,93 в обоих сценариях происходит уничтожение раковых клеток без явных проявлений симптомов заболевания. При среднем уровне повреждения иммунной системы F = 0,67 и тех же начальных условиях динамика изменения концентрации аномальных клеток в первом сценарии приводит к образованию опухоли; во втором сценарии медленное развитие раковой опухоли позволяет вовремя выработать нужное количество иммунных элементов. При значительном поражении иммунной системы F = 0,46 происходит неограниченное деление аномальных клеток, которое приводит к достижению опухоли критических размеров, т.е. образование выходит за границы органа, и можно говорить о наступлении стадии метастазирования.

С использованием имитационного моделирования на основе метода Монте-Карло проведено 500 численных экспериментов, в результате которых набрана статистика, позволяющая оценить риск развития раковой опухоли. Результаты моделирования показаны на рис. 6; анализируя график, можно увидеть, что при функциональности иммунной системы меньше F = 0,4 риск возникновения опухоли равен 0,495, что может привести к смертельному исходу в случае, если не будет оказано медицинское вмешательство. Таким образом, даже при полной дееспособности иммунной системы F = 1 риск возникновения опухоли с данным набором параметров отли- скорости деления с учетом функциональности иммунной системы

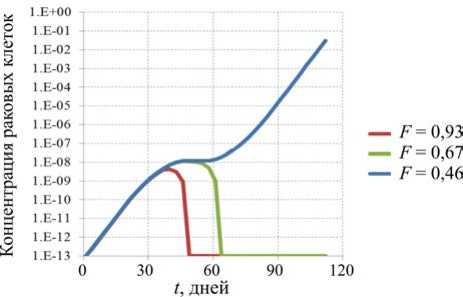
Рис. 5. Динамика роста опухоли с малым параметром скорости деления с учетом функциональности иммунной системы

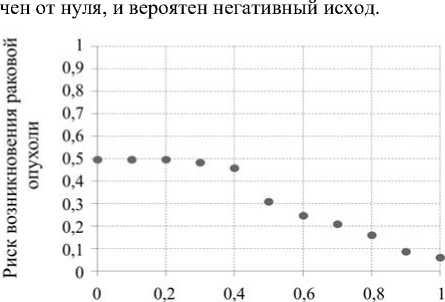
Функциональное нарушение иммунной системы

Рис. 6. Результаты моделирования исходов динамики роста раковой опухоли с учетом влияния функциональности иммунной системы

Выводы. Предложенная прогностическая математическая модель позволяет качественно описать процесс возникновения и изменения количества аномальных клеток с учетом механизма ангиогенеза, быстрые и медленные процессы образования и роста опухолей. Предложен подход для оценки влияния химических факторов среды обитания на динамику онкологической опухоли. Проведена оценка влияния параметров, определяющих состояние организма (иммунной системы), и характеристик аномальных клеток на течение и исход онкологического заболевания. Использование данного подхода позволяет определить элементы, функциональность которых в первую очередь определяет ход онкологического процесса. Приведенная модель представляет собой упрощенное описание сложных взаимодействий многочисленных регуляторных систем, происходящих при формировании опухоли и процессах ее развития. Однако она дает возможность анализа взаимодействия множества регуляторных систем, связанных с данными процессами. В отличие от лабораторных наблюдений за образцами, которые позволяют уви- деть только опухолевые структуры на момент отбора тканевых образцов, математическое моделирование позволяет определить принципы динамической эволюции опухоли и условия формирования каждой культуры аномальных клеток.

Изучение воздействия негативных факторов среды обитания на возникновение раковых опухолей имеет важное социально-экономическое значение. Это позволяет прогнозировать распространение раковых заболеваний, а также разрабатывать эффективные меры по предотвращению этих заболеваний и улучшению качества жизни населения, проживающего на территориях с неблагоприятным состоянием среды обитания.

Финансирование. Результаты получены при выполнении государственного задания Министерства науки и высшего образования Российской Федерации на выполнение фундаментальных научных исследований (проект FSNM-2023-0003).