Прогноз рождаемости при моделировании роста численности населения

Проблема прогнозирования роста численности населения является одной из ключевых, решаемых в рамках анализа демографической ситуации. На уровне отдельных популяций (стран, регионов, м^ъшш-пальных образований и т.п.) в основе прогнозирования лежат модели, описывающие динамику естественного прироста населения с учетом миграционных процессов. Для глобального прогнозирования роста народонаселения в масштабе Земли используются более сложные модели, основанные на теории гиперболического роста и демографического перехода.

Впервые проблему математического описания закономерностей роста населения и «возможного» перенаселения Земли поднял известный экономист

Томас Роберт Малыше. Главным постулатом своей теории Мальтус считал следующую закономерность: «Население, если не метать его свободном)' воспроизводству, удваивается каждые 25 пет, иначе говоря - в геометрической прогрессии. В то же время объемы ресурсов, необходимых для поддержания жизни, растут лишь в прогрессии арифметической» [Malthus. 1798] Такое утверждение приводило к ограничению роста народонаселения и появлению эффекта перенаселения.

Б середине XX в. теория Мальтуса была опровергнута серией исследований в области изучения глобальных демографических процессов, начало которым было положено Форстером [Foerster, Мж Mora, Amiot, 1960] и Хостером (1975). ГЪлучсн-ныс эмпирические модели переросли в теорию дс-

电 Кирьянов Д. А., 2016

мографического перехода, что повлияло как на теоретические представления о демографических процессах, так и на использование прикладных методов прогнозирования роста народонаселения.

Современные представления о глобальных де-мографических процессах с позиции формального описания феномена демографического взрыва к демографического перехода были сформулированы СП Капицей [1992-1999].

Следует отметить, что современные исследования в области моделирования демографических процессов вполне допускают использование «классических» подходов, основанных на экспоненциальных логистических функциях роста, для описания динамики численности на ограниченных временных отрезках для относительно небольших (в масштабе человечества) групп населения. В работах А.В₊ Коротаева, А С. Малков 乱 Д₊А. Халтуриной (2005-2012) представлен критический анализ методов математического моделирования роста народонаселения. В частности, в работе «Математическая модель роста населения Земли, экономики, технологии и образования» авторы выделяют границы применимости различных теорий для демографического прогнозирования [Коротаев. Мал- кое. Халтурина* 2005].

Модели роста численности населения

Математические методы^ основанные на классических теориях

Численность населения является универсальной мерой практически всех социально-экономических процессов, протекающих в обществе, доступной для непосредственного измерения, наблюдения и анализа. Поэтому именно этот локауте ль был и является объектом внимания исследований в об* ЛДСТИ изучения социальных, экономическихР исторических и прочих процессов.

В основе классического представления процесса роста численности населения лежит закон сохранения. который позволяет представить изменение численности населения в виде дифференциального уравнения где N - число людей： В - число рождений； D -число смертей в единиц времени.

Представленное уравнение описывает т₊н. естественное движение населения, свойственное «закрытым системам». Учет миграционных перемещений позволяет переписать (1) б виде

——В — Г) — divJ %         (2)

dt где N - число людей; В - число рождений; D -число смертей в единицу времени; вектор J соот ветствует миграционному потоку.

Исследования в области демографии показывают. что все переменные правой части зависят от многих других социальных параметров, и в том числе от «человеческого фактора» - принятия решений отдельными людьми, слабо поддающегося формализации. Таким образом, единственным пока доступным подходом ЯВ.1ЯСТСЯ макроописание, не вдающееся в мелкие детали демографического процесса и описывающее дннамнку больших людских масс, для которых влияние человеческого фактора заметно ниже.

В XIX в** при моделировании численности населения человек рассматривался как биологический ВИД, что ЯВЛЯЛОСЬ основанием ДЛЯ ВОЗМОЖНОГО ИСПОЛЬЮБЗНИЯ моделей ПОПУЛЯЦИОННОЙ динамики [Ризниченко, 2002].

Базовой моделью* описыБающей динамику популяции ЖИВОТНЫХ, является логистическая модель. предложенная Вер?аольстом [VerhulsL 1838];

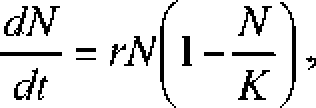
которую можно также представить в виде

К .

Логика уравнения ⑶ такова: роадаемость at является постоянной ； таким образом, число рождений В = U]N пропорционально численности по-п ) 'ляции, естественная смертность 如 также считается постоянной, а квадратичная добавка bN± в выражении для полной смертности D 二 a 〕 N+b№ возникает нзз ограниченности ресурса* не позволяющей популяции бесконечно расти. Коэффициент b называют коэффициентом внутривидовой конкуренции.

Динамика поп ) ^гляции. описываемая логистическим уравнением, имеет еле 冲 ощий вид. Вначале, когда численность популяции мала, наблюдается экспоненциальный рост с показателем г = а 】一 / Затем, по мере заполнения экологической ншші, рост замедляется и. в конечном счете, численность популяции выходит на постоянный уровень К, который определяет равновесное состояние численности при заданных ресурсных ограничениях и определяет пределы ее роста.

Другой известной популяционной моделью ЯВ" ляегся модель Лотки-Вольтерра [Вольтерра. 1976丄 известная как «хищник-жертва». Она описывает динамику популяций двух взаимодействующих видов, один из которых является основной пищей для другого, и состоит из двух уравнении вида (1)

—-Ах- Вху 小                          (4)

где X - численность жертв, у - численность хищников, А, В, С, D - коэффициенты.

Данная модель демонстрирует циклическою динамику. Рост численности жертв приводит к росту хищников, рост хищников вызывает сокращение жертв, сокращение жертв ведет к сокращению хищников, а при малом количестве хищников жертвы вновь начинают бурно размножаться.

Модели логистического роста и «хищник-жертва» для решения задан прогнозирования численности населения имеют очень ограниченное прикладное значение, так как человеческая популяция обладает способностью к преобразованию условий существования, а это приводіп к снижению влияния внешних условий на динамику численности.

Тем не менее, в обзоре [Коротаев, Малков, Халтурина, 2005] выдвигается тезис, что модель (4) находит новое, нетрадиционное применение в демографических моделях. В частности, она может быть применена для описания колебаний численности населения, обнаруженных практически у всех аграрных обществ [Капица, 1992]. В роли жертвы выступает население, а в роли хищника -социальная нестабильность, войны, голод, эпидемии, вероятность возникновения которых увеличивается по мере того, как растущее население приближается к потолкут несущей способности.

Модели ги перболи чес ісого роста

В основе теории гиперболического роста народонаселения лежит эмпирическая закономерность, обнаруженная Форрестером, Мора и Эм йотом в 1965 году [Foerster, Von, Mora, Ainiot, I960]. Они провели статистическою оценку^р демографически 工 данных и обнаружили, что кривая роста населения Земли лучик всего а ппроксимируется кривой 上，            (5)

где С и tn - константы, причем S - соответствует 13 ноября 2*)26 г. Согласно этой фор 風 у ле в этот день численность человечества должна уйтм в бесконечность.

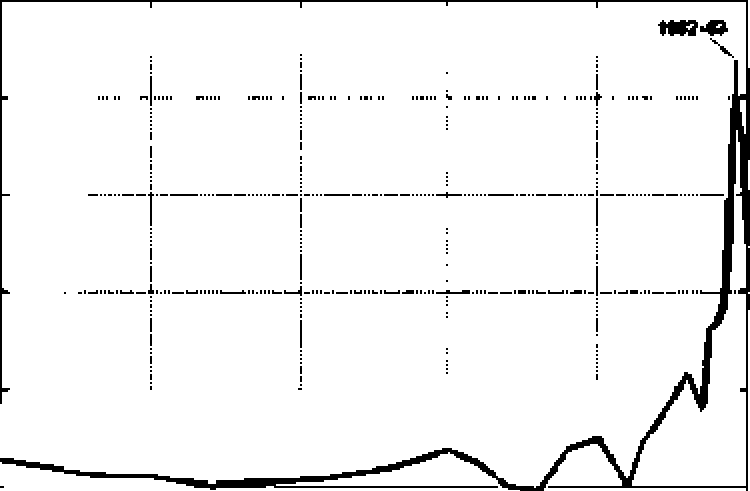
Обна руженна я Форестером за кономерность была оп}ғбликована в I960 г., в то время, когда гиперболическая зависимость выражалась наиболее явно. Начиная с 60-х гг. XX в., реальная динамика народонаселения Земли стала все больше отходить от гиперболической кривой, и к настоящему времени темпы роста населения резко понизились (рис 1).

*кк зр      nt      WW      1ИР      ЗИП

Рис+ L Темпы роста населения Земли

Наблюдаемое снижение темпов роста численности населения получило название глобального демографического перехода. Описание Этого явления является предметом многих современных исследований в области демографического анализа и прогнозирования. При этом исследователям и решается двойственная проблема ： описание явления гиперболического роста, который наблюдался в течение многих тысячелетий и демографического перехода с временным масштабом десятки лет.

Наиболее фундаментальными работами в области глобальной демографии, описывающим и демографические процессы и дающими ответы на оба поставленных вопроса, по праву считаются работы СП Капицы [1992, 1999].

В отличие от демографических моделей, строящихся на биологических предположениях типа (1)-(4). что рост населения пропорционален самому населению, то есть, по сути, в предположении, что рождаемость и смертность мало меняются, со временем Капица предлагает использовать квадратичную зависимость для скорости роста dN N² 力 c

Уравнения вида (6) хорошо изучены и их решения известны как режимы с обострением. Характерная черта таких уравнений состоит в том, что в некоторый конечный момент времени to решение уходит в бесконечность.

Что же касается самого уравнения ⑹， то его решением как раз н будет полученная эмпирически формула (5), где 厶 зависит от начальных условий. Таким образом, уравнение (6) удовлетворительно описывнет эмпирическую зависимость (5) и может выступать в роли модели демографического процесса.

Причиной явления гиперболического роста, по мнению С П. Капицы, является социальная сущность самого человека, которая обеспечивает информационный обмен между отдельными индивидами.

Поскольку рост человечества, согласно уравнению ⑹， зависит исключительно от размера популяции к не зависит ни от каких внешних условий к ресурсных ограничений, то логика диктует искать причину демографического перехода также внутрн человека, поскольку никакие ресурсные ограничения не могли на протяжении тысячелетий остановить процесс роста* да и в нынешнее время переход происходит не из-за ресурсного кризиса, так как поду^гшевой доход постоянно расгет. Для Капицы особо важным параметром видится характерное время жшнм человека т = 42 года, определяемое «внутренней предельной способностью системы человечества и человека к развитию» [Капица_к 1992].

Для того чтобы описать демографический переход. Капица предложил уравнение, полученное на основе (5) и (6): dN

⑺

力 （ "-E ） ‘ 十 г

где т- характерное время жизни человека*

Полученное уравнение уже нс даст обострения -ухода решения в бесконечность. Напротив, при такой модификации численность населения стабилизируется на уровне 10-12 млрд чсл.? что согласуется с прогнозами демографов.

Тем нс мснсс, ни основное уравнение (6), НИ его модификация (7), описывающая эффект дсмо-графическ0ro перехода, не раскрывают сути действующих законов, оставаясь на феноменологическом уровне констатацией обнаруженной эмпирической закономерности. С математической точки прения, имеющиеся демографические данные - это реализация некоторого процесса, интегральная кривая, а равнения (6) и (5) эквивалентны, по-скольк5г одно является дифференциальной формой записи другого.

Обоснование причин возникновения явлений гиперболического роста и демографического перехода является предметом критики феноменологической модели С П. Капицы и. вместе с тем* мотивацией ученых для проведения исследований в этой области.

Интересен подход к моделированию численности народонаселения, основанный на предположении о возможности перехода сознания человека меж^ двумя мирами - тонким и плотным, в ре-зультате процессов рождения и смерти. В религии это явление принято называть реинкарнацией. Мо-делЬк предложенная Л.М. Гиндилисом [2001] объясняет феномен гиперболического роста и демо-графическ0ro перехода циркуляцией населения меж^ мирами.

Материалистические объяснения указанных феноменов возникают при рассмотрении взаимного влияния численности населения и создаваемых им технологий. Наиболее математизированной и разработанной работой в этой области представляется исследование Майкла Кремера [Kremer* 1993]一 В нем представлены сразу несколько моделей, с разных сторон описывающих процесс взаимного роста численности населения и уровня технологии. Представленные Кремером модели указывают на существенную роль экономических факторов при объяснении изменений рождаемости и смертности. В итоге работа М. Кремера дала очень серьезное и правдоподобное описание гиперболического роста населения Земли, опираясь, преаде всего, на экономические механизмы и давая при этом не худшие результаты, чем теория С П. Капицы. Однако в той части, где она касалась демографи ческого перехода, ее объяснение все еще нельзя считать достаточным, даже несмотря на сильное усложнение модели и введение нескольких дополнительных параметров.

Попытка объяснить явление демографического перехода, найти объективные причины пределов роста была предпринята в работах А+В. Подлазова [2001]+ Он, с одной стороны, видит причины гиперболического роста в совместном процессе роста человечестБа и технологии, а с другой - причин)' демографи ческого перехода он ищет в самом естестве человека“ его биологических параметрах и продолжительности жизни. Модель гиперболического роста АВ Подла зов записывает в виде

⑻

— = NP, di где N - численность населения, а Р - уровень технологии.

В отличие от М. Кремера, для которого технологии -это средство производства продукта А В. Подлазов видит роль технологий иначе. Он вводит понятие жизнесберегающие технологии Роль технологий он видит в предотвра щении смерти и продлении жизни безотносительно того, каким образом это достигается - за счет производства пищи или за счет религиозных норм морали.

Развитие жизнесберегающих технологий приводит к сохранению здоровья, следствием чего является снижение смертности и увеличение продолжительности жизни. Особенно этот факт проявляется при рассмотрении динамики младенческой смертности. Вместе с тем, развитие технологий приводит к изменению демографических уста-новоЕС следствием чего является снижение рождаемости.

Анализ большой статистической выборки убедительно показывает, что рост уровня образования населения в ходе модернизации, наряду с развитием медицинских технологий к системы социального обеспечения, является веющим фактором сни- жения по сравнению с обществами, уже завершившими демографический переход, к которым относится и Россия, влияние образования и здравоохранения на рождаемость особо велико для стран третьего мира. При этом появление и распространение новых медицинских технологий возможно только в результате развития сферы образования. Образование, с одной стороны, позволяет населению ознакомиться со средствами рефляции рождаемости, а с другой - меняет ценностные ориентации людей, что отражается и на репродуктивных установках [Коротаев. Малков. Халтурина. 2005].

Таким образом, современное представление о динамике населения в условиях демографического перехода при гиперболическом росте основано на взаимодействии трех важных показателей - численность населения, уровень технологии и уровень П ) амотности. При ее простоте и малом количестве параметров модель с высокой точностью описывает совместную динамику всех трех показателей в рассматриваемом интервале с начала нашей эры по нынешнее время. При этом показано, что определяющим признаком, характеризующим демографический переход, является снижение рождаемости.

Прогнозирование рождаемости

Выполнение практических расчетов по прогно-зированию численности населения для небольших, в сравнении со всей человеческой популяцией, территориях (страны, регионы) связано с построением системы балансовых уравнений притока и оттока населения для отдельных возрастных групп. В демографии такой подход принято называть методом передвижки возрастов.

Одной из задач, связанных с применением метода передвижки возрастов, является оценка числа родившихся за каждый временной период прогно-зіфования (обычно год). Для решения этой задачи стандартным является метод, основанный на коэффициентах рождаемости по возрасту матери. При этом население других возрастных групп в расчетах не участвует. В свете представленного обзора по теории гиперболического роста и демографического перехода прирост населения определяется всей половой и возрастной струкілрой, определяющей демографические установки.

Для исследования этого утверждения была выполнена статистическая обработка данных о половой и возрастной структуре населения Пермского края за период 2010-2014 гг. в разрезе муниципальных образований.

Дизайн исследования заключался в выявлении влияния структуры населения на рождаемость с использованием регрессионного анализа. В качестве обучающей выборки использовались данные за 2010 г., а проверка построенных моделей выполнялась по данным за последующие годы. На основании полученных моделей проводится оценка качества предсказания и устойчивости полученных зависимостей.

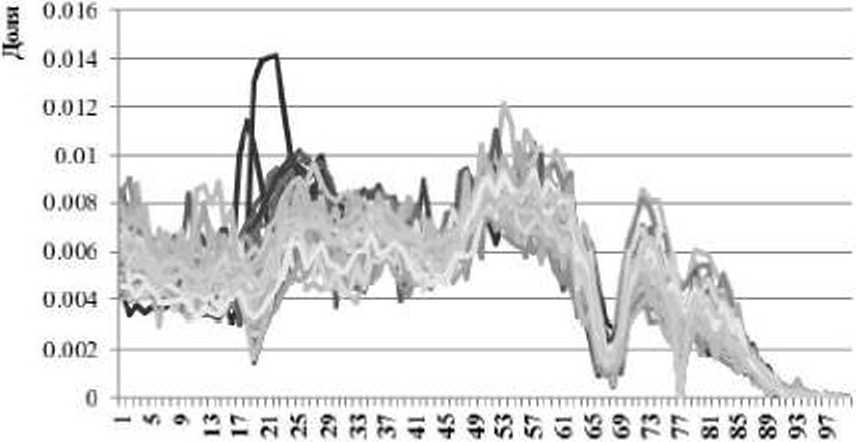
Обучающая выборка представляет собой данные о структуре населения млниципальных образований Пермского края в 2010 г. На рис. 2 приведено распределение данных в разрезе однолетних возрастных групп для лп жчин и женщин.

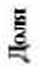
0.014

0 012

0.01

0.008

0 006

0 004

0.002

О

Возраст

Boipaci

б)

Рис. 2. Распределение струкпры населения в разрезе однолетних возрастных групп: а - ьіужчины, б - женщины

Из рис. 2 видно, что структура населения распределена существенно неравномерно, как по возрастным группам, так и по территориям. Для выявления структурных закономерностей было выполнено преобразование данных методом главных компонент. В табл. 1 приведены величины собственных значений, превышающих 1.

Большое количество записей в табл. 1 свидетельствует о наличии большого количества переменных в исходных данных, слабо корреллирую-щих между собой. Такое обстоятельство затрудняет выбор структур связанных переменных в исходных данных. Для сокращения числа использованных главных компонент, описывающих вариации данных, воспользуемся методом «каменистая осыпь». На рис. 3 приведен графнк «каменистой осыпи».

Из ірафика, представленного на рис. 3, следует, что для описания структурных связей между переменными в исходной матрице данных достаточно использовать 5 главных компонент.

М73-М83, F23, F25-F32, F36, F52, F53, F70-F84;

• -третья ГК М5, М23, М26, М28, М34, М3 9, М41, F3 3-F3 5, F3 9, F40, F42, F45;

• -четвертая ГК Ml8, М59, М61, F37, F55-F59, F61;

пятая ГК М16-М17, F16-F17, F41-F43.

Из матрицы исходных данных можно выделить ряд структурных закономерностей по связям с главными компонентами:

• -первая ГК М1-М4, М6-М15, М42-М55, М57-58, М65-М69, М72, М84-М85, F1-F15, F18-F22, F24, F44, F46, F47, F49, F50, F60, F62-F69;

• -вторая ГК М19-М22, М24-М2 5, М27, М29-МЗЗ, М3 5-М3 8, М40, М56, М60, М63, М70-М71,

Таблица 1

Значение собственных значений, превышающих 1

Фактор	Собственное значение	% общей дисперсии	Накопленное собственное значение	Накопленный % дисперсии
1	43.30946	25.47615	43.3095	25.47615
2	35.35243	20.79555	78.6619	46.27170
3	16.84322	9.90778	95.5051	56.17948
4	10.89335	6.40785	106.3985	62.58733
5	5.65951	3.32912	112.0580	65.91645
6	5.06011	2.97654	117.1181	68.89299
7	4.29375	2.52574	121.4118	71.41872
8	3.74957	2.20563	125.1614	73.62435
9	3.15774	1.85749	128.3191	75.48185
К)	2.95707	1.73945	131.2762	77.22130
11	2.81128	1.65370	134.0875	78.87500
12	2.50926	1.47604	136.5968	80.35103
13	2.47746	1.45733	139.0742	81.80836
14	2.22304	1.30767	141.2973	83.11603
15	2.04168	1.20099	143.3389	84.31702
16	1.89586	1.11521	145.2348	85.43223
17	1.83186	1.07757	147.0667	86.50980
18	1.70568	1.00334	148.7723	87.51314
19	1.55018	0.91187	150.3225	88.42501
20	1.48753	0.87502	151.8100	89.30003
21	1.37761	0.81036	153.1877	90.11038
22	1.28131	0.75371	154.4690	90.86409
23	1.23813	0.72831	155.7071	91.59240
24	1.16820	0.68717	156.8753	92.2795 8
25	1.09664	0.64508	157.9719	92.92466
26	1.05847	0.62263	159.0304	93.54729

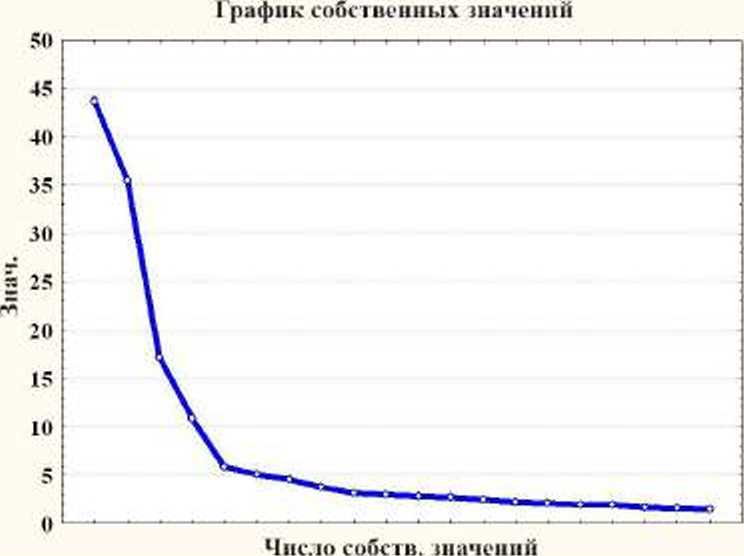
Рис. 3. График «каменистая осыпь»

Анализ связей исходных переменных с после

дующими главными компонентами не позволяет выявить значимых структурных закономерностей. Для получения моделей зависимостей влияния структуры населения на рождаемость был выполнен линейный множественный регрессионный анализ на главные компоненты. При этом в качестве зависимых переменных использовалась рождаемость, дифференцированная по полу, а в качестве независимых - значение главных компонент для каждого муниципального образования Пермского края. Параметры полученных моделей приведены в табл. 2-3.

Из табл. 2-3 видно, что влияние населения, находящегося в фертильном возрасте, на рождаемость наблюдается только для рождения мальчи- ков, причем это влияние не является определяющим. Большую часть дисперсии рождаемости описывается главными компонентами L 3, 5, которые в основном характеризуют либо детское население, либо население старших возрастов* Из этого следует* что рождаемость определяется не только и не столько наличием женщин и мужчин фертильного возраста, а демографическими установками, кото рые формируются за счет преобладания в структуре населения детей и взрослых старших возрастов. Такое утверждение является спорным с точки зрения классической демографии, но в рамках проведенного анализа может быть использовано в качестве аргумента, подтверждающего высоесий вклад демографических установок и мотиваций в увеличение роадаемости.

Таблица 2

Парамет]>ы регрессии для рождаемости мальчиков МО (R2=0*41)

	БЕТА	Стандартная ошибка БЕТА	В	Стандартная ошибка В	t(49)	Уровень значимости
Свободный член			0,006316	0.000124	51.119528	0.000000
Фактор 1	0.418702	0.109417	0,000477	0.000125	3,826647	0.0003 69
Фактор 3	0 3 36600	0.109417	0.0003 84	0.000125	3.076292	0.00 3 42 5
Фактор 5	0,273 345	0.109417	0.000312	0.000125	2498187	0.015888
Фактор 2	0 223686	0.109417	0,0002 5 5	0.000125	2.044 3 3 7	0.046313

Таблици 3

Па]>аметры ] ) егрессии для ] ) ояиаемости девочек Ғ0 (К=0*47)

БЕТА Стандартная ошибка БЕТА В Стандартная ошибка В t(50) Уровень значимости Свободный член - 0.006101 0.000111 55.018828 0.000000 Фактор 3 0.456760 0.103129 0.000496 0.000112 4.429010 0.000052 Фактор 1 0,403099 0.103129 0.00043 R 0,000112 3.90X680 0.0002S0 Фактор 5 0.311611 0.103129 0.0003 3 8 0.000112 3.021564 0.003 957 девочек по обдающей выборке.

Предсказанные м наблюдаешве значешя Завмсиыая перемен.: МО

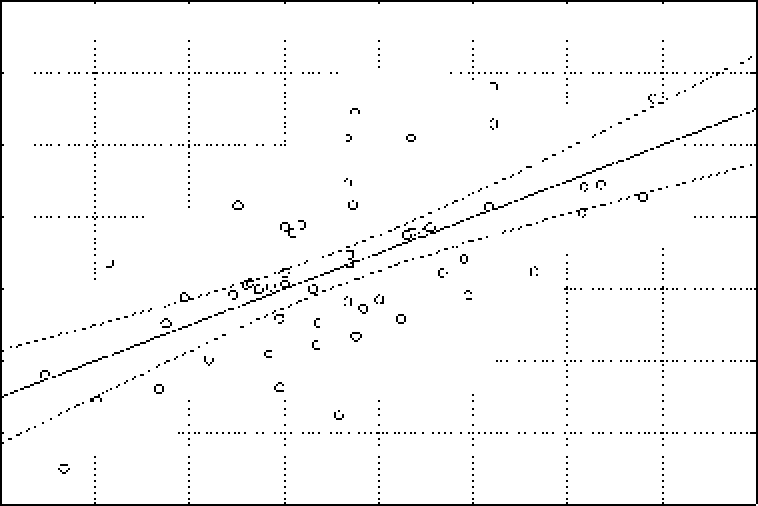
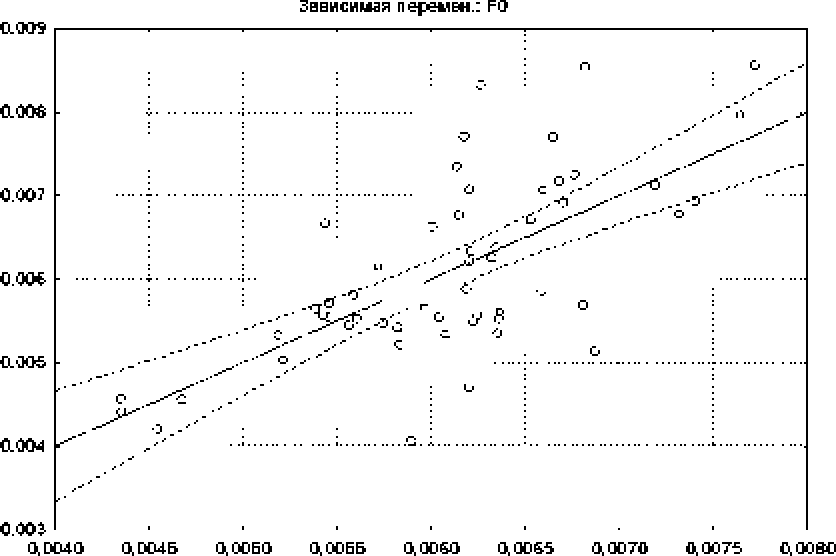
На рис. 4 представлена диип ) амма рассеивания прогнозных значений рождаемости мальчиков и

Q.D1O 口口峭 0.О0Ө

I Q.DQ7

J 口口 06

О.ОСЙ

0 3                           R 口陋口 4

Предек, качения                  | доверит. |

Предсвязанше и маблюдаеше значения

Прщ^ск. хачЁния                 「 и 、 ад% Aoeeptn. I

б)

Рис. 4. Диаграмма рассеивания прогнозных значений рождаемости по обучающей выборке:

а)

а - малвчикн, 6 - девочки

Результаты прогнозирова ння не дают основание утверждать о высоком качестве модели (R2=O,41 для мальчиков, R‘=U,47 для девочек). Следовательно, за счет структуры населения мы можем объяснить меньше половины дисперсии рождаемости.

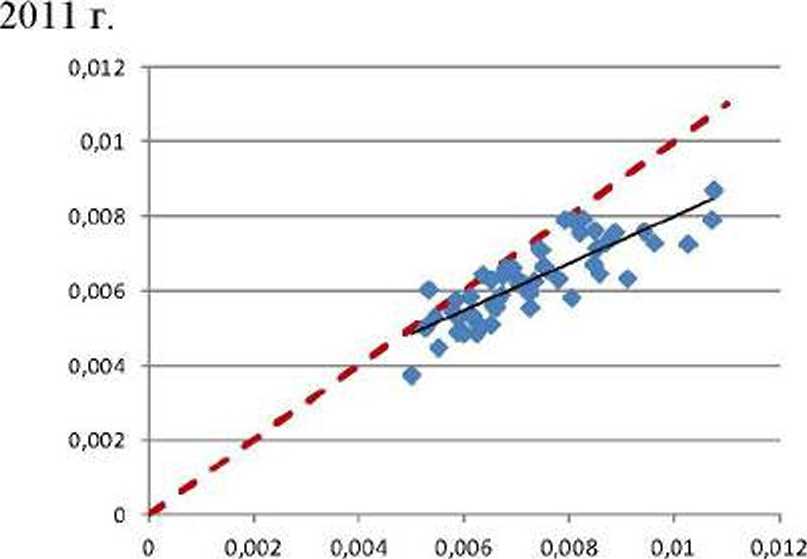
Проверка устойчивости пожженных зависимостей выполнялась на данных за 2011-2014 гг. На рис. 5 приведены диаграммы рассеивания для предсказания рождаемости мальчиков и девочек за

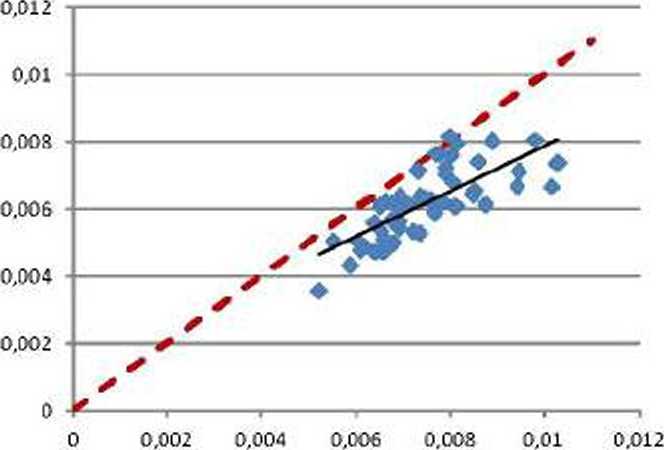
На рис. 6 приведены диаграммы рассеивания прогнозных значений рождаемости мальчиков и девочек за 2014 г.

а)                                                        б)

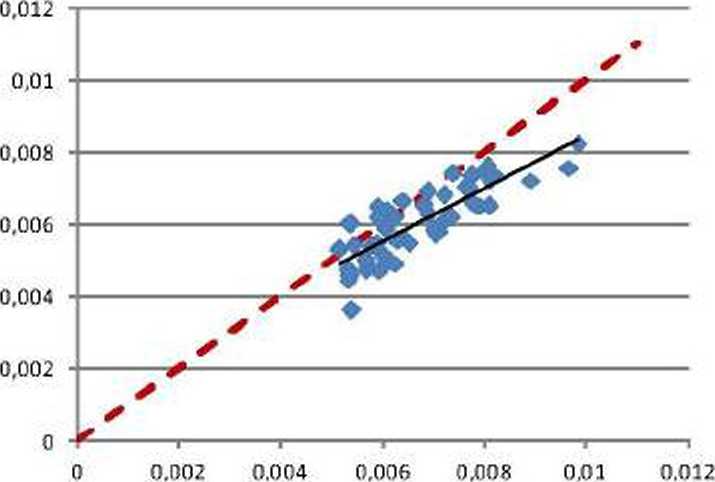
Рис. 5. Графики предсказанных и реальных значений рождаемости мальчиков и девочек за 2011 г.: а - мальчики (R2=0.154), б - девочки (R2=0.391)

а)                                                       б)

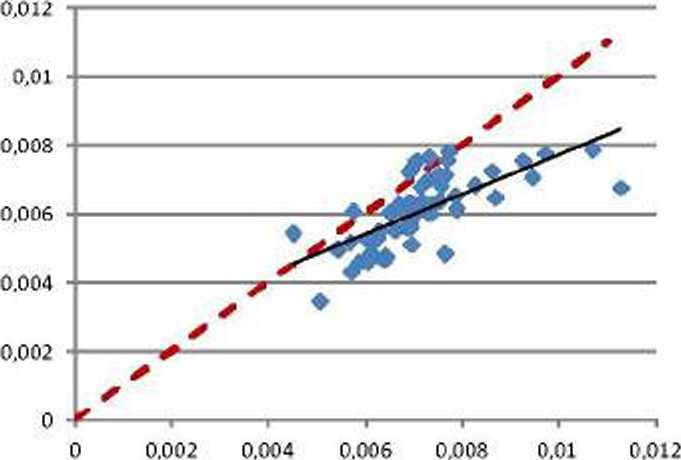
Рис. 6. Графики предсказанных и реальных значений рождаемости мальчиков и девочек за 2014 г.: а - мальчики (R2=0.128), б - девочки (R2=0.046)

Сопоставление рис. 4-6 показывает, что в целом полученная зависимость обладает устойчивостью во времени, по крайней мере, за пятилетний период, в рамках которого проводилось настоящее исследование. Вместе с тем. следует отметить, что качество предсказаний падает по мере удаления от временного периода, соответствующего обучающей выборке, причем модель дает заниженные оценки. Это говорит о том, что использование по-щ-чаемых моделей в результате регрессионного анализа имеет ограниченный диапазон использования и может быть применим для прогнозирования не более чем на десять лет.

В демографии такого рода прогнозные оценки широко распространены при выполнении прогнозов в промежутках времени іиеаду переписями населения, которые проводятся примерно один раз в десять лет. При этом каждая перепись населения позволяет верифицировать полученное модели и обеспечить их корректное применение на следующее десятилетие.

Заключение

В ходе выполнения работы был изучен ряд тп бликаций ученых по теме «моделирование наро донаселения», которые отражают современные представления о демографических процессах, протекающих в глобальном (мировом) масштабе. В исследованиях конца XX - начала XXI в. делается вывод о независимости роста численности населения от ресурсного обеспечения, при этом рост численности населения определяется уровнем жизнесберегающих технологий и грамотности. В условиях глобального демографического перехода существует мировая тенденция к снижению рождаемости и стабили:з<щии численности.

На более мелких масштабах на рассмотрение процесса роста численности населения, существен-ную роль играет роадасмость. которая определяет способность населения к самовоспроизводству. Стандартный метод расчета числа рождений определяется долей женщин фертильного возраста в структуре населения и является основой для выполнения большинства демографических прогнозов. Моделирование зависимостей рождаемости от половозрастной структуры населения на примере Пермского края не подтверждает данного утверждения. Более того, роль женщин фертильного возраста по влиянию на рождаемость значительно ниже, чем влияние других возрастных групп.

Таким образом, полученные результаты свиде-Т^ЛЬСТБуЮТ в целом о ВЛИЯНИИ структуры населения на коэффициенты рождаемости, но при этом нс полностью объясняют вес вариации. Поиск факторов. которые могли бы улучшить сам}г модель и качество предсказаний является предметом дополнительных углубленных исследований.

Би бл иограф и чески й список

Волылерра 8 Математическая теория борьбы за существование / под ре 工 Ю. М. Свирежева. М: Наута, 1976. 287 с.

Гиндине *?А£ Рост народонаселения в модели с реинкарнацией // Дельфис. 2001. № 26 С 55-6 L

Капица С Я. Математическая модель роста населения мира // Математическое моделирование. 199Z Г 4, №6 С 65-79.

Капица С П. Сколько людей жило, живет и б\^гдет жить на земле, М.: Наука, 1999+117 с.

Коротаев А.В., Малков А С., Халтурина Д А. Мате-мапіческая модель роста населения Земли, экономики, технологии и образования. М., 2005, 41 с

Подлая 4 氏 Основные уравнения теоретической 口 емогра 巾 ии и модель глобального демоцзафиче-ского перехода: препринт / Институт прикладной математики им. МВ Келдыша РАН. М* 200 L № 88. 16 с.

Резниченко Г.Ю. Лекции по математическим моделям б биологии. Ижевск. 2002. Ч. 1. 232 с₊

Foerster, Von 笈， Mora P., n\AAmiot L Doomsday: Friday, 13 November, AD 2026 // Science. 1960. Vol 132. R 1291-1295.

Kremer, 力金 Population Growth and Teclmological Change: One Million BC to 1990 // The Quarterly Journal of Economics. 1993. Vol. 108. P. 681-716,

Xia!thus, Г. Population ： The First Essay, Aim Arbon Ml: Universih⁷ of Micliigan Press, 179g.

Verhulsl F+F Notice sur la loi que la population suit dans son accroisscmcnt // Corr. Math. Et Phys. 1838. Vot 10. P. 113-121

Об авторе

Кирьянов Дмитрий Алексаңдрович. к.т.н. заведующий отделом математического моделирования систем и процессов

доцент кафедры экологии человека и безопасности жизнедеятельности

ФГБОУВО «Пермский государственный национальный исследовательский университет» 61499" Пермь, ул. Букирева, 15