Прогнозирование адаптационного потенциала травянистых многолетников

Природная среда влияет на формирование экобиоморф травянистых многолетников. Габитус варьирует в зависимости от эколого-фитоценотических условия обитания вида. Знание особенностей формирования продуктивных признаков растений в зависимости от факторов местообитаний, позволяет рассчитать продуктивность вида в различных сообществах, и тем самым, оптимизировать ресурсные изыскания в отношении хозяйственно-ценных видов. Обсуждается построение многофакторной регрессионной модели и вероятностные оценки точности решения задачи, характеризующие как степень взаимосвязи формирования продуктивных признаков растений и экологических факторов среды, так и информационную ценность биометрических баз данных.

МАТЕРИАЛЫ И МЕТОДЫ

Для построения модельной структуры экобиоморф, использовались геоботанические описания и база биометрических данных модельного вида Thalictrum minus L. (Белых, 2012). Из 7 пунктов расположенных на территории Южной Сибири от 82° 56' до 104° 14' восточной долготы. В качестве данных для определения параметров    абиотических факторов       использовался свободно распространяемый архив высот SRTM [, разрешение 3″ (ок. 90 м) по широте и долготе], на основе которого в каждой точке исследуемой территории оценивались параметры: высота над уровнем моря (метры), крутизна склона

(радианы), экспозиция склона (радианы), освещенность по сомкнутости крон, проективное покрытие травостоя.

В работе предлагается подход с позиций системного анализа, а именно многофакторное прогнозирование, основанное на том, что для оценки формирования продуктивных признаков предлагается многофакторная регрессионная модель (Рис. 1).

По каждому фактору были созданы прогнозные модели с применением базы экспертных данных. По последним моделям делаются прогнозы, результаты которых используются в многофакторной модели.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

При построении модели множественной регрессии отбор факторов, включаемых в уравнение регрессии, является одним из основных условий ее качества, заключающегося в соответствии формы модели теоретической концепции и в точности предсказания на рассматриваемом интервале времени наблюдаемых значений переменной уравнением регрессии (Клиланд, 1974; Антонов, 2004). Отбор факторов при построении модели множественной регрессии обычно осуществляется на основе качественного теоретико-экологического и статистического анализа тенденций изменения рассматриваемых процессов. На этапе обоснования модели регрессии возникает проблема выбора оптимального состава независимых факторов среди ряда альтернативных вариантов.

Наш подход предполагает первоначально включить в модель все отобранные на этапе теоретического анализа факторы. Уточнение их состава производится на основе анализа характеристик качества построенной модели, одной из групп которых являются и показатели, выражающие силу влияния каждого из факторов на независимую переменную y. При этом в модель включаются все факторы, отобранные в ходе теоретического анализа проблемы. Для этого варианта модели рассчитываются значения оценок коэффициентов модели, их стандартные ошибки и значения t- критериев Стьюдента. Затем из модели удаляется незначимый фактор, который характеризуется наименьшим значением t- критерия, и таким образом формируется новый вариант модели с уменьшенным на один числом факторов. При этом в модели может быть несколько незначимых факторов. Этап отбора факторов можно считать законченным, когда остающиеся в модели факторы являются значимыми. Если при этом полученная модель удовлетворяет критериям адекватности, то процесс построения модели считается завершенным в целом. В настоящей работе для прогнозирования эволюционного потенциала биоморф были рассмотрены: модель множественной линейной регрессии и нелинейные степенные регрессионные модели.

Для оценки экологических особенностей изучаемого вида Thalictrum minus L.

первоначально были использованы разработанные ранее региональные экологические шкалы, на основе увязки показателей обилия растений и определенных экологических факторов. При этом основой для составления экологических показателей служит правило экологической индивидуальности растений Л.Г. Раменского, согласно которому растения каждого вида имеют свою определенную амплитуду по отношению к действию любого экологического фактора (Цыганов, 1983).

На первом этапе анализа влияния экологических факторов рассматривались следующие факторы 7 местообитаний вида Thalictrum minus L. : x1 – высота над уровнем моря, x2 – общее проективного покрытие, x3 – сомкнутость крон, x4 – содержание гумуса в почве, влияющие на развитие следующих индикационных признаков: y1 – высота растения (см), y2 – длина листа (см), y3 – ширина листа (см), y4 – средняя длина междоузлий (см), y5 – длина соцветия (см), y6 – диаметр стебля (мм), y7 – содержание сапонинов.

Были оценены показатели статистической связи между каждой из объясняемых (зависимых) переменных yj и указанным набором объясняющих переменных – факторов или регрессоров xi. В качестве таких показателей были выбраны парные коэффициенты корреляции, точечные оценки которых приведены в таблице 1.

Данные корреляционного анализа по районам Южной Сибири (таблица 2) дают хорошую картину. Высокие значения коэффициентов корреляции между всеми показателями развития растений yj и x2 , x4 свидетельствуют о прямой связи анализируемых характеристик с общим проективным покрытием и содержанием гумуса. Именно эту связь можно описывать линейными регрессионными моделями. Такие факторы, как местоположение и освещенность дают устойчивую линейную связь со всеми характеристиками растений.

Этап моделирования влияния экологических факторов местообитаний: x 1 , x 2 , x 3 , x 4 , на характеристики растений: y 1 , y 2 , y 3 , y 4 , y 5 , y 6 , y 7

состоял в построении эконометрических моделей линейной парной и множественной регрессий с анализом и обсуждением полученных результатов.

Линейные модели, построенные по методу наименьших квадратов (МНК), по 7 ценопопуляциям имеют вид: y1 =56,46-0,031 x2 +10,86 x3 +8,98 x4 , R²= 0,72; y2 =20,97-0,41 x2 +4,92 x3 +4,07 x4 ,   R²= 0,92;

y3 =47,11-1,06 x2 -3,85 x3 +8,25 x4 ,    R²= 0,93;

y4 =15,34-0,33 x2 +3,31 x3 +3,17 x4 ,    R²= 0,82;

y5 =-11,12+0,29 x2 -13,68 x3 +3,59 x4 , R²= 0,82; y6 =0,63-0,01 x2 +0,03 x3 +0,16 x4 ,      R²= 0,75;

y7 =1,35-6,89 x2 -0,309 x3 -0,01 x4 ,      R²= 0,87.

Здесь коэффициенты оцененных регрессий характеризуют среднее абсолютное изменение у , когда соответствующий регрессор меняет свои значения на одну единицу (в единицах измерения х и у ). Показатели степени пригодности построенных моделей – коэффициенты детерминации R² свидетельствуют о хорошей подгонке данных. Так, если содержание гумуса ( x4 ) увеличить на 1%, то ширина листа ( y3 ) увеличится на 8,25% от среднего значения.

Таким образом, данная модель позволяет прогнозировать поведение травянистых многолетников в условиях интродукции при увеличении освещения и технологических способах регулирования агроэкологических условий.

Построение нелинейной степенной модели для факторов, имеющих большую связь с результирующими показателями, привело к следующим результатам: y1 =3,66 x2 ^0,76 x4 ^0,14,     R²= 0,81;

y2 =77,66 x2 ^-0,77 x4 ^1,06, R²= 0,87;

y3 =431,22 x2 ^-1,32 x4 ^1,52, R²= 0,92;

y4 =11,33 x2 ^-0,28 x4 ^0,81, R²= 0,74;

y5 =0,006 x2 ^1,84 x4 ^0,36,    R²= 0,97;

y6 =0,16 x2 ^-0,04 x4 ^0,92,    R²= 0,86;

y7 =0,63 x2 ^0,24 x4 ^-0,13,     R²= 0,21.

Степень подгонки данных достаточно высока, о чем свидетельствует коэффициент детерминации R2. В этих моделях показатели степени представляют собой эластичности параметров растений по факторам x2 – общего проективного покрытия и x4 – содержания гумуса. Так, при увеличении общего проективного покрытия на 1% от своего среднего значения, высота растения y1 увеличивается на 0,76% от своего среднего значения, а при увеличении содержания гумуса на 1% – эта высота увеличится лишь на 0,14%, и т.д. Соотношение между содержанием сапонинов (y7) и общим проективным покрытием (x2) и содержанием гумуса (x4) слабо выражено, так как степень подгонки данных нелинейной моделью составляет лишь 21%.

Описанные закономерности могут служить валидным критерием для экологического мониторинга природных территорий.

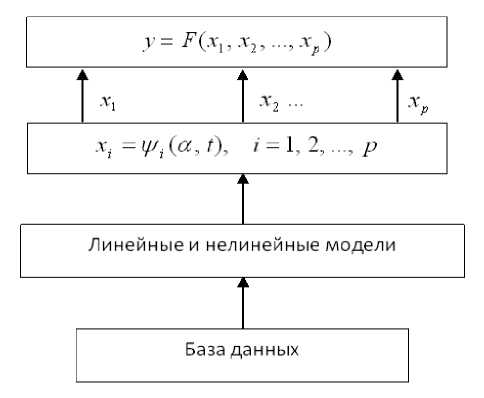
Рисунок. 1 Общая схема многофакторного прогнозирования потенциала экобиоморф в зависимости от эколого-ценотических условий произрастания

Здесь y - значение прогнозируемого показателя; F - функция регрессии; Ψi - прогнозные функции для факторов; α - набор параметров функции Ψi ; xi - значение i -го фактора; p - число факторов; t – время.

Таблица 1 : Значения корреляции по южносибирским ценопопуляциям

	y1	y2	y3	y4	y5
y1	1
y2	0,904777	1
y3	0,912376	0,981526	1
y4	0,93939	0,921638	0,934133	1
y5	0,876739	0,810747	0,86017	0,813384	1
y6	0,946365	0,950927	0,957607	0,886652	0,892822
y7	-0,05812	-0,21907	-0,10473	-0,28265	0,116764
x1	0,081948	0,257989	0,086232	-0,00538	-0,17005
x2	0,802913	0,809302	0,812063	0,761778	0,893388
x3	-0,1399	0,002627	-0,1378	-0,0033	-0,40433
x4	0,844582	0,916477	0,922106	0,865237	0,887956

Продолжение Таблицы 1.

	y6	y7	x1	x2	x3	x4
y6	1
y7	-0,03876	1
x1	0,151386	-0,32737	1
x2	0,781306	0,039502	0,049753	1
x3	-0,12405	-0,88195	0,544696	-0,37013	1
x4	0,855691	-0,08901	0,0675	0,963096	-0,24856	1

Таблица 2 : Результаты наблюдений по ценопопуляциям различной эколого-географической приуроченности

	y 1	y 2	y 3	y 4	y 5	y 6	у 7	x 1	x 2	x 3	x 4
Танзыбейская	193	43	62	32	59	1,56	1,06	850	95	0,6	14,3
Онинская	160	32	48	22	54	1,38	1,22	520	74	0,3	9,1
Бегрядинская	111	26	31	13	20	0,83	1,15	1200	68	0,6	7,1
Абазинская	100	20	25	15	26	0,58	1,08	450	64	0,6	6,3
Канжульская	106	23	33	16	18	0,64	1,20	475	62	0,3	6,8
Кошелюхинская	151	29	42	20	57	1,08	1,26	500	95	0	11,8
Капказакская	134	21	26	17	22	0,73	1,17	700	62	0,5	5,2

ЗАКЛЮЧЕНИЕ

Для прогнозирования адаптационного потенциала биоморф травянистых многолетников в градиенте эколого-фитоценотических условий предложено многофакторное прогнозирование, основанное на том, что для оценки, развития продуктивных признаков формирующихся под влиянием эколого-ценотических факторов местообитаний, предлагается многофакторная регрессионная модель.

Созданная многофакторная модель оценки перспективности адаптационного потенциала биоморф травянистых многолетников, исходя из решаемой задачи, выбранных моделей и сведений экспертов, позволяет прогнозировать формирование продуктивных признаков в зависимости от местоположения площади, условий освещенности, густоты стояния травостоя и богатства почвы.

В работе показано, что для прогнозирования формирования продуктивных признаков достаточно учитывать небольшое количество факторов (сомкнутость крон, густота травостоя и содержание гумуса), обеспечивая при этом необходимую точность прогноза.