Прогнозирование динамики потребления электроэнергии в России на основе линейной многофакторной модели

Развитие энергетики в целом и электроэнергетики в частности, выражающееся не только в увеличении объёмов потребляемой энергии, но и в расширении её источников и повышения эффективности производства, во многом определяет темпы экономического роста страны. По сравнению с другими видами энергоносителей, электроэнергия используется во всех сферах человеческой деятельности, является ключевой движущей силой роста мировой энергетики.

Так по данным Росстата, динамика потребления электроэнергии в Российской Федерации за период с 2006 по 2014 г. свидетельствует о положительной тенденции, что в свою очередь поднимает вопрос о решении таких проблем как: нерациональное и избыточное потребление электроэнергии и повышение эффективности её использования. На 2014 год этот показатель равен 1059041,8 ГВт\ч.

Проблемы математического моделирования объёмов потребления электроэнергии в условиях современного развития оптового рынка электроэнергии и мощности приобретают особое значение. В силу штрафных санкций со стороны поставщиков при отклонении реального потребления от заявленного ранее, крупные энергопотребители заинтересованы в составлении точных заявок планируемого объёма потребления энергии на оптовом рынке электроэнергии и мощности. Производители электроэнергии заинтересованы в прогнозах энергопотребления с целью оперативного реагирования на колебания спроса и оптимального развития инфраструктуры [1]. От достоверности построенных прогнозов потребления электроэнергии во многом зависят эффективность решений по управлению энергопотреблением, возможности экономии энергоресурсов и экономичность режимов работы всей энергосистемы в целом.

Из работы [1] были выделены следующие факторы, которые могут влиять на показатель потребления электроэнергии в РФ:

• •    x₁ - Численность населения со среднедушевыми денежными доходами ниже величины прожиточного минимума \ За период, миллион человек

• •    x₂ - Индекс цен производителей промышленной продукции: Производство, передача и распределение электроэнергии \ Темп роста к предыдущему периоду, 1991г=1

• •    x₃ - Экспорт: электроэнергия \ За период, гигаватт-час

• •    x₄ - Средние цены производителей на продукцию: газ горючий природный (естественный) \ За период, рублей за 1000 кубических метров

• •    x₅ - Средние цены производителей на продукцию: нефть добытая \ За период, рублей за тонну

Таблица 1

Выбор факторов для модели

Фактор	Причина включения в модель
x 1	C экономической точки зрения оказывает воздействие на процесс потребления электроэнергии. Чем выше значение фактора, тем ниже потребление электроэнергии.

x 2	Потребление электроэнергии промышленными производствами зависит от индексов промышленного производства, производств важнейших видов промышленной продукции, индексов цен на энергоресурсы, непосредственно определяющие тарифы на электроэнергию.
x 3	Дополнительный фактор
x 4	ГЭС – ресурсы газовых электростанций
x 5	ТЭС – ресурсы тепловых электростанций

Из числа доступных временных рядов выберем управляемые x₂ [2], x₃ и неуправляемые x₁ , x₄ , x₅.

Широко распространенным методом повышения социально-экономических показателей является информационная поддержка принятия решений, позволяющая при помощи экономических (эконометрических) моделей прогнозировать развитие систем и выбирать решения, ведущие к наибольшему росту их эффективности.

Для моделирования социально-экономических систем применяются:

• •    Трендовые модели (ТрМ, развитие системы показывается через тренд её основных показателей [3])

• •    Линейные многофакторные модели (ЛММ, зависимость факторов и критериев)

• •    Авторегрессионные модели (АвРМ, зависимость от предыдущих состояний временного ряда)

• •    Модели в пространстве состояний (МПС, зависимость от состояния внешней среды)

Наиболее подходящими для задач прогнозирования считаются факторные модели: линейная многофакторная модель и модель в пространстве состояний [4]. Прогнозирование по модели предполагает выбор факторов ( x_i ), напрямую или косвенно влияющих на критерий ( y ), выбор вида модели, построение модели, проверку на возможность прогнозирования, определение горизонта прогнозирования и экстраполяцию построенной модели.

В качестве критерия ( y ) разумно выбрать потребление электроэнергии в стране (За период, гигаватт-час). Для исключения влияния размерности данных нормируем их по формуле

'         •V-mmCt.-G))

• X. (Г) =----;—г^-----гг-

• max(x,(t))-min(x,(f))

где x_t - элемент временного ряда, min( x, ( t ) ) - минимальное значение элемента временного ряда, max( x , ( t )) - максимальное значение элемента временного ряда.

Традиционным является анализ предварительно выбранных факторов с точки зрения их взаимной корреляции. Факторы с высокой взаимной корреляцией подлежат исключению из большинства моделей.

Анализ факторов показал, что из числа выбранных ничего исключать не нужно – все коэффициенты корреляции находятся в пределах допустимых значений.

Построим линейную многофакторную модель потребления электроэнергии и рассчитаем коэффициенты модели методом наименьших квадратов (МНК, минимизируем квадрат разности статистических данных и расчетных):

^(O^+S^XO

S^Cv^tO-J^O))1 -* ”™ где a0 – независимый коэффициент, ai – коэффициенты влияния i-х факторов xi(t) в момент времени (номер года) t на значение критерия.

Минимизацию произведем с помощью мастера поиска решения в MSExcel . В результате получены следующие коэффициенты ЛММ модели: a₀ = 2,5211; a₁ = -1,7374; a₂ = -0,9706; a₃ = -0,0966, a₄ = -0,2675, a₅ = -1,1309, где наиболее значащим факторам стал x₁ , далее по значимости влияния на критерий идут x₅иx₂ Квадратичная погрешность аппроксимации ЛММ S = 0,0620 (Рис.1).

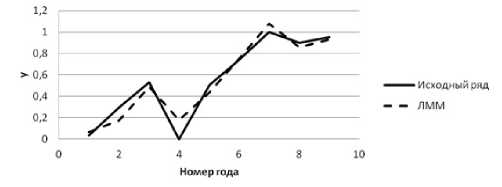
Рис. 1. Аппроксимация исходных данных ЛММ

Из рис.1 видно, что модель неплохо аппроксимирует данные и ее можно использовать для проведения прогноза, но также проверим возможность использования АвРМ.

Авторегрессионные модели 1-го, 2-го и 3-го порядков имеют вид:

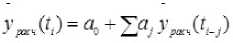
где: N – порядок модели; a₀ , a₁ – коэффициенты модели.

При помощи мастера «поиск решения» MS Excel получаем коэффициенты:

Авторегрессионная модель 1-го порядка: a₀ = 0,1332, a₁ = 0,9821; квадратичная погрешность аппроксимации S = 0,3024.

Авторегрессионная модель 2-го порядка: a₀ = 0,1625 , a₁ = 0.6928, a₂ = 0,3 квадратичная погрешность аппроксимации S = 0,3034.

Авторегрессионная модель 3-го порядка: a₀ = 0,1879 , a₁ = 1,044, a₂ = -1,3783, a₃ =1,6866; Квадратичная погрешность аппроксимации S = 0,1301. (Рис.2)

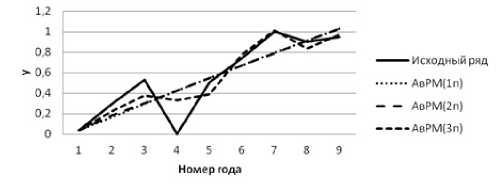
Рис. 2 Аппроксимация исходных данных АвРМ

Проанализировав график АвРМ разного порядка, можно сделать вывод, что наиболее хорошо аппроксимирует исходные данные модель с порядком N =3, где её квадратичная погрешность аппроксимации ниже, чем у остальных.

Соберем все квадратичные погрешности аппроксимаций в одну таблицу (Таблица 3).

Таблица 2

Погрешности аппроксимации всех моделей

Модель	ЛММ	АвРМ 1-го порядка	АвРМ 2-го порядка	АвРМ 3-го порядка
s	0,0620	0,3024	0,3034	0,1301

Так как целью настоящей работы является поддержка принятия решений по уменьшению энергопотребления в будущем, нас интересуют не только погрешность аппроксимации, но и прогнозные свойства получаемых моделей (Рис.3). Для проверки возможности прогнозирования применим широко распространенный метод постпрогноза [5], заключающийся в расчете реакции системы по модели при известных рядах факторов на протяжении нескольких последних лет. Как показано в работе [6], увеличение интервала постпрогноза позволяет определить также горизонт прогнозирования.

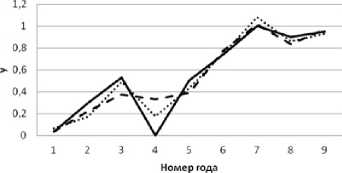
Рис. 3 Анализ приближения моделей к y(t)

Для всех вышеописанных моделей произведем расчет постпрогноза на 1, 2 и 3 года (Рис.4).

Постпрогноз линейной многофакторной модели

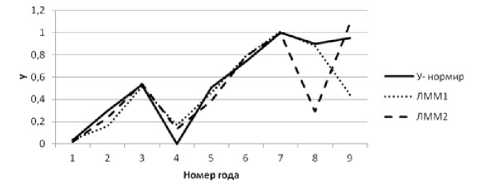
Рис. 4 Постпрогноз по ЛММ

На рис 4. изображены постпрогнозы только на 1 и 2 года, так как график на 3 года отклонился далеко от этих значений по оси y до -49.

Постпрогноз авторегрессионной модели 3-го порядка (Рис.5).

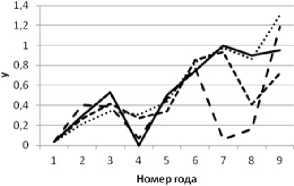
^^^— Исходный ряд|у)

.......УрасчАвРМ(1)

- -—- ¥расч АеРМ(2)

--Урасч АвРМ(З)

Рис. 5 Постпрогноз АвРМ

Таблица 3

Отклонение постпрогноза различных моделей от исходных данных

Модель / Постпрогноз	1 год	2 год	3год
ЛММ	-46,8%	12,5%	-4660,8%
АвРМ(3п)	27.0%	-31,8%	19,8%

Исходя из данных в таблице 4, можно сказать, что наименьшую погрешность при постпрогнозе на 3 года имеет АвРМ, наихудшую ЛММ, однако авторегрессионная модель непригодна для исследования реакции системы на изменения факторов, потому что не учитывает влияние факторов на критерий и не позволяет рекомендовать управленческие решения. Исходя из этого, горизонт прогнозирования необходимо ограничить двумя годами.

При постпрогнозе на 2 года погрешность ЛММ лучше, чем у АвРМ третьего порядка, это значит, что данные постпрогноза на 2 года у ЛММ выглядят более правдоподобно по отношению к исходным данным. Это позволяет выбрать именно её для дальнейшей работы.

Спрогнозируем развитие системы в зависимости от влияния неуправляемых факторов x₁ , x₄ , x₅ и управляемых x₂ , x₃ .

Тенденцию развития этих факторов определим, сравнивая в пределах горизонта прогнозирования ряд значений фактора и его приближения линейной x ( t ) = a + b * t и квадратичной x ( t ) = a + b * t + c * t ² моделями. Коэффициенты этих моделей также найдем с помощью МНК с применением мастера поиска решения. Выбор вида трендов определим с помощью величины достоверности аппроксимации R² (Таблица 4).

Таблица 4

Выбор вида тренда для факторов по R ²

x i	Лин.	Квадр.
x 1	0,3487	0,9453
x 2	0,4441	0,9992
x 3	0,94	0,9521
x 4	0,922	0,9442
x 5	0,1263	0,7536

Из всех R² для управляемых и неуправляемых факторов была выбрана квадратичная тенденция развития.

Спрогнозируем все факторы на 2 года исходя из выбранной модели (Таблица 5)

Таблица 5

Прогноз факторов на 2015 и 2016 г.

x расч	2014	2015	2016
x 1	0,1129	0,5443	1,2088
x 2	0,1806	-0,058	-0,4438
x 3	0	-0,4321	-0,9778
x 4	1	1,0456	1,0405
x 5	0,841	0,647	0,3198

Полученные прогнозом значения факторов подставим в нашу модель ЛММ и, используя рассчитанные коэффициенты модели ( a₀ - a₅ ) получим прогнозное значение критерия на 2015-2016 год.

Прогноз энергопортебления на 2015-2016 г. линейной многофакторной моделью, при спрогнозированных неуправляемых ( x₁ , x₄ , x₅ ) и управляемых ( x₂ , x₃ ) факторах представлен на Рис.6.

При любом развитии неуправляемых факторов энергопотребление в стране снижается.

Теперь изменим на ± 5% тенденции развития неуправляемых факторов, и получим прогнозы развития системы на 2 года (Рис.7).

Из-за большого количества вариаций управления тре- мя факторами (27 значений), для удобного восприятия на графике оставлены значения худшей и лучшей ситуации при x1 ± 5%.

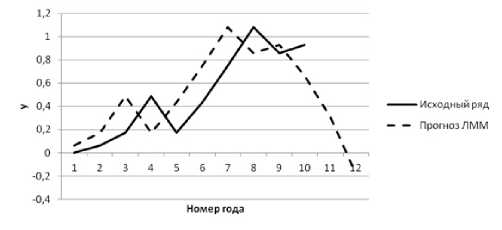
Рис. 6 Прогноз критерия (y) по ЛММ

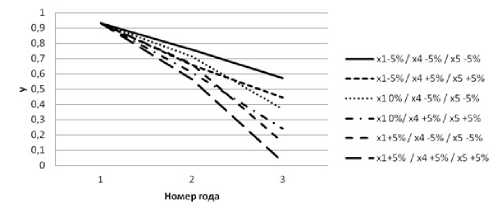
Рис. 7 Прогноз критерия при малых изменениях неуправляемых факторов

Наихудшим вариантом развития ситуации при неуправляемых факторах является уменьшение x₁ , x₄ , x₅ на 5%. Наилучшим является обратное увеличение всех факторов на 5%, при котором достигается уменьшение критерия на 1113%.

Исследуем возможность компенсации негативного влияния неуправляемого фактора путем изменения управляемых факторов x₂ , x₃ . Для этих факторов, образом аналогичным описанному выше, так же были определены тенденции развития (Таблица 4). Изменяя факторы на ± 5%, получим прогноз развития системы на 2 года вследствие решения ЛПР.

Наилучшим результатом изменения управляемых факторов является сочетание из x₂ - 5%, x₃ -5%, что приводит к значению критерия 0,52209. Он на 8,9% лучше, чем в наихудшем варианте развития системы без управления.

При этом значение 0,52209 меньше, чем 0,57331 (наихудший вариант развития событий при неуправляемых факторах). Следовательно, даже при наихудшем сочетании изменений тенденций неуправляемых факторов, ЛПР в состоянии не только сохранить позитивную тенденцию развития системы, но и улучшить ее на 70,6%.

Проверим значимость факторов и их оправданность включения в модель. Целью изменения факторов является снижение потребления электроэнергии (Таблица 6).

Таблица 6

Проверка и объяснение выдвинутых гипотез

Фактор	Гипотеза	Резуль-тат	Возможное объяснение
x 1	Чем меньше численность населения с среднедушевым денежным доходом ниже прожиточного минимума, тем энергопотребление больше.	Да	Население может позволить увеличить потребление электроэнергии исходя из своих доходов.

x 2	Чем больше темп роста индекса цен производителей промышленной продукции, тем меньше будет потребляться электроэнергии населением.	Да	Индекс цен производителей влияет на тарифы предоставляемых услуг. Соответственно, чем больше индекс, тем дороже тарифы. Чем дороже тарифы, тем меньше население будет использовать электроэнергию.
x 3	Чем больше экспорт произведенной электроэнергии, тем меньше энергопотребление.	Нет	Увеличивая экспорт электроэнергии, мы не уменьшим её потребление, так как население по-прежнему использует его на прежнем уровне. Увеличивая экспорт, необходимо будет увеличивать и производство электроэнергии.
x 4 , x 5	Чем больше цены на ресурсы для электростанций, тем меньше потребление электроэнергии.	x 4 - Да x 5 - Н 5 ет	Возможное объяснение кроется в рамках глобального спроса и предложения в нефтегазовой экономике[7].

Проведя исследования, можно сделать следующие выводы:

• •    Основной фактор, который в значительной степени оказывает влияние на энергопотребление – это x₁ (Численность населения со среднедушевыми денежными доходами ниже величины прожиточного минимума). Так как этот фактор является неуправляемым, то его уменьшение сильно скажется на энергопотреблении - оно увеличится, что повлечет за собой строительство новых электростанций для увеличения объема производства электроэнергии в лучшем случае или увеличение цен на тарифы в худшем.

• •    Фактором x₂ можно замедлить повышение энергопотребления в стране, путем его увеличения.

• •    Фактор x₃ не оказывает существенного влияния на потребление электроэнергии.