Прогнозирование и классификация индекса качества грунтовых вод с использованием регрессионных моделей обучения

Наличие воды, необходимой для орошения, бытовых и промышленных целей, обеспечивается за счет грунтовых вод во всем мире. Из-за демографического бума и высоких темпов индустриализации спрос на пресную воду значительно вырос за последние не- сколько десятилетий. Поставки и качество грунтовых вод в большей степени страдают из-за быстрой урбанизации, чрезмерного использования и ненадлежащего удаления мусора, особенно в городских районах развивающихся стран, таких как Индия. По оценкам ВОЗ качество воды является основной причиной 80% болезней человека [5]. После загрязнения качество грун-

• ©    Кертикеян Махамуни - научный сотрудник кафедры вычислительной техники

• ©    Рошан Джеймс - научный сотрудник кафедры вычислительной техники

  
  
  
  
  
  

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

товых вод невозможно восстановить путем удаления загрязняющих веществ из источника. Таким образом становится крайне важным регулярно проверять состояние грунтовых вод и сохранять их с соблюдением достаточных мер предосторожности.

Одной из практических альтернатив управления является внедрение показателей качества воды для обеспечения полной оценки параметров качества воды как в поверхностных, так и в грунтовых водах. Состояние качества воды можно изучить с помощью математического инструмента, известного как индекс качества воды, который основан на важных факторах качества воды, таких как мутность, содержание органических веществ, температура, электропроводность, pH и следы металлов. Индекс качества воды показывает, является ли вода чистой, немного загрязненной или сильно загрязненной по шкале от 0 до 100. Алиас и соавт. [2] обнаружили, что антропогенная деятельность частично загрязнила реку. Пробы воды, взятые в восьми точках вдоль реки Семеных, также были сильно загрязнены фосфатами и фекальной кишечной палочкой [4]. Сложность задачи измерения каждого из этих параметров грунтовых вод связана с большими затратами и трудоемкостью процесса.

В течение последних трех десятилетий для оценки качества грунтовых вод для питьевых целей применялись различные подходы с использованием моделей искусственного интеллекта (ИИ), что повышало эффективность по сравнению с статистическими методами [1; 2; 4; 11; 12; 15; 23]. Моделирование на основе искусственного интелекта быстро генерирует значения индекса качества воды и исключает расчеты субиндексов. Кроме того, методы машинного обучения успешно использовались в Индии для определения параметров качества воды.

Джалори и соавт. [17] использовали модель дерева решений для прогнозирования пяти показателей качества воды. В другом исследовании [20] для построения точной стратегии прогнозирования качества воды для «умного сельского хозяйства» была рекомендована глубокая двунаправленная простая рекуррентная единица. Для прогнозирования качества воды Шафи и соавт. [29] предложили четыре алгоритма машинного обучения для классификации качества воды, 25 параметров использовались в качестве входных параметров в одинарной упреждающей нейронной сети [6]. Tyagi и соавт. использовали четыре различные модели машинного обучения для прогнозирования индекса качества воды иранской реки Карун. Автор использовал модель регрессии опорных векторов с различными ядрами.

Методы искусственного интеллекта, такие как метод опорных векторов (МОВ), метод наименьших квадратов (МНК) и искусственная нейросеть (ИНС)

[16; 22], также использовались для прогнозирования индекса качества воды в реке. Хотя метод опорных векторов представил отличный прогноз, недостатком было то, что требовалось протестировать четыре функции ядра, прежде чем определить лучшую. Также требуется множество параметров, каждому из которых необходимо присвоить оптимальные значения. Среди алгоритмов искусственного интелекта у искусственной нейросети есть несколько недостатков, включая низкую мощность прогнозирования, когда тестовые данные находятся за пределами диапазонов обучающих данных в небольшом наборе данных. Для решения этих проблем был разработан ANFIS [9].

В [24], поскольку для сбора данных требуется больше датчиков, авторы использовали только 10 факторов, что дорого обходится. Другие доступные регрессионные модели в статье тоже игнорируются. Модель, на которую приходится более 99,5% изменчивости данных, была разработана Газзазом и соавт. [14] для прогнозирования индекса качества воды. Они использовали 23 характеристики для прогнозирования индекса качества воды с использованием датчиков интернет-вещей. Однако они не могут предсказать растворенный кислород (РК) в реальном времени.

Для прогнозирования индекса качества воды используются лабораторные тесты и модели искусственного интелекта. Однако каждая модель имеет некоторые ограничения и работает с разными наборами данных [26; 27]. Анализ временных рядов или статистические методы используются в обычных процедурах моделирования качества грунтовых вод. Эти методы работают на предположении, что зависимые и независимые переменные также связаны между собой. Им часто требуются данные для удовлетворения определенных статистических требований, таких как нормализация и т.д.. С другой стороны, модели, основанные на искусственном интелекте, не должны делать никаких предположений о данных. Азад и соавт. [8] использовали адаптивную нейро-нечеткую систему вывода ( ANFIS ) для прогнозирования параметров качества воды. Согласно их исследованиям, модель ANFIS имела наилучшую точность в прогнозировании электропроводности и жесткости воды на этапе тестирования с R ² = 0,98, RMSE = 73,03 и MAPE = 5,16. Гибридная искусственная нейронная сеть (ГИНС) с моделью генетического алгоритма была разработана Жангом и соавт. [32] для водоочистных сооружений в Китае, которые использовали 45 местоположений. Прогнозируется, что за счет увеличения предоставленных обучающих данных производительность модели гибридной искусственной нейронной сети увеличится с 0,71 до 0,93 по параметру R ².

Основная цель данного исследования – спрогнозировать индекс качества воды для штата Тамилнад с ис-

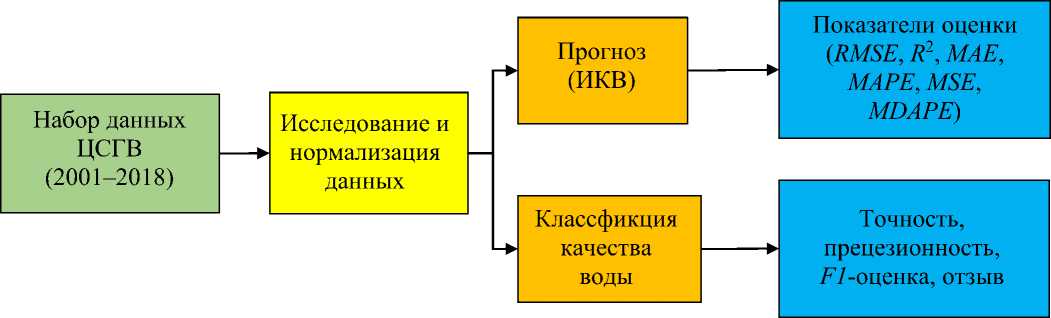
Рис. 1. Cтруктура модели прогнозирования индекса качества воды с использованием методов машинного обучения

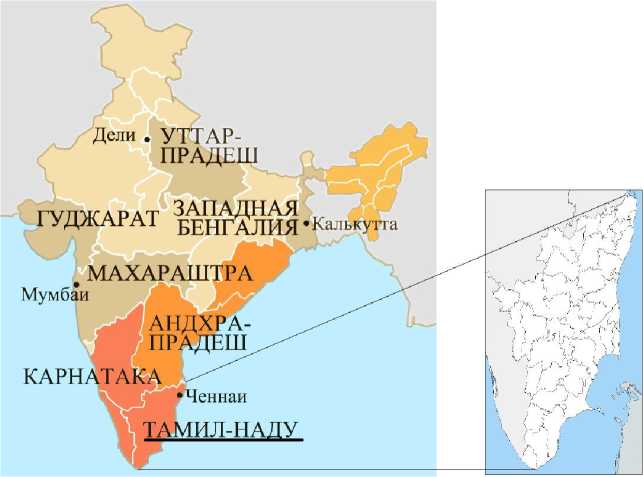
Рис. 2. Исследуемые районы штата Тамилнад

пользованием данных Центрального совета по грунтовым водам (ЦСГВ) и определить качество грунтовых вод в нескольких районах.

Материалы и методы

Целью данного исследования является внедрение различных моделей машинного обучения для прогнозирования показателей качества грунтовых вод. На рис. 1 показана структура моделей машинного обучения для базы данных ЦСГВ.

Область исследования

Значения параметров качества грунтовых вод для районов штата Тамилнад (рис. 2), соответствующие 2001–2018 годам, были получены от Центральной комиссии по грунтовым водам Индии. ЦКГВ собрала эти образцы в конце засушливого сезона, перед началом сезона дождей. В зависимости от штата это будет либо в апреле, либо в мае. Всего по районам Тамилнада было собрано 3619 единиц данных.

Подготовка данных и расчет индкса качества воды

Отсутствие данных в наборе данных было устранено и была применена нормализация. Чтобы поместить набор данных в пространство меньшей размерности с отличной разделимостью по классам и свести к минимуму чрезмерную подгонку, используется анализ главных компонент (АГК), который является «неконтролируемым» методом. Он игнорирует метки классов и стремится определить основные направления, которые максимизируют дисперсию в наборе данных. Результаты анализа главных компонент используются для выбора индексных скважин с целью долгосрочного мониторинга качества грунтовых вод. Основываясь на нескольких параметрах качества воды, индекс качества воды выдает единое значение, которое выражает общее качество воды в определенном месте и в определенное время. Здесь для расчета индекса качества воды использовались 10 переменных, таких

Таблица 1

W i и RW по параметрам качества воды

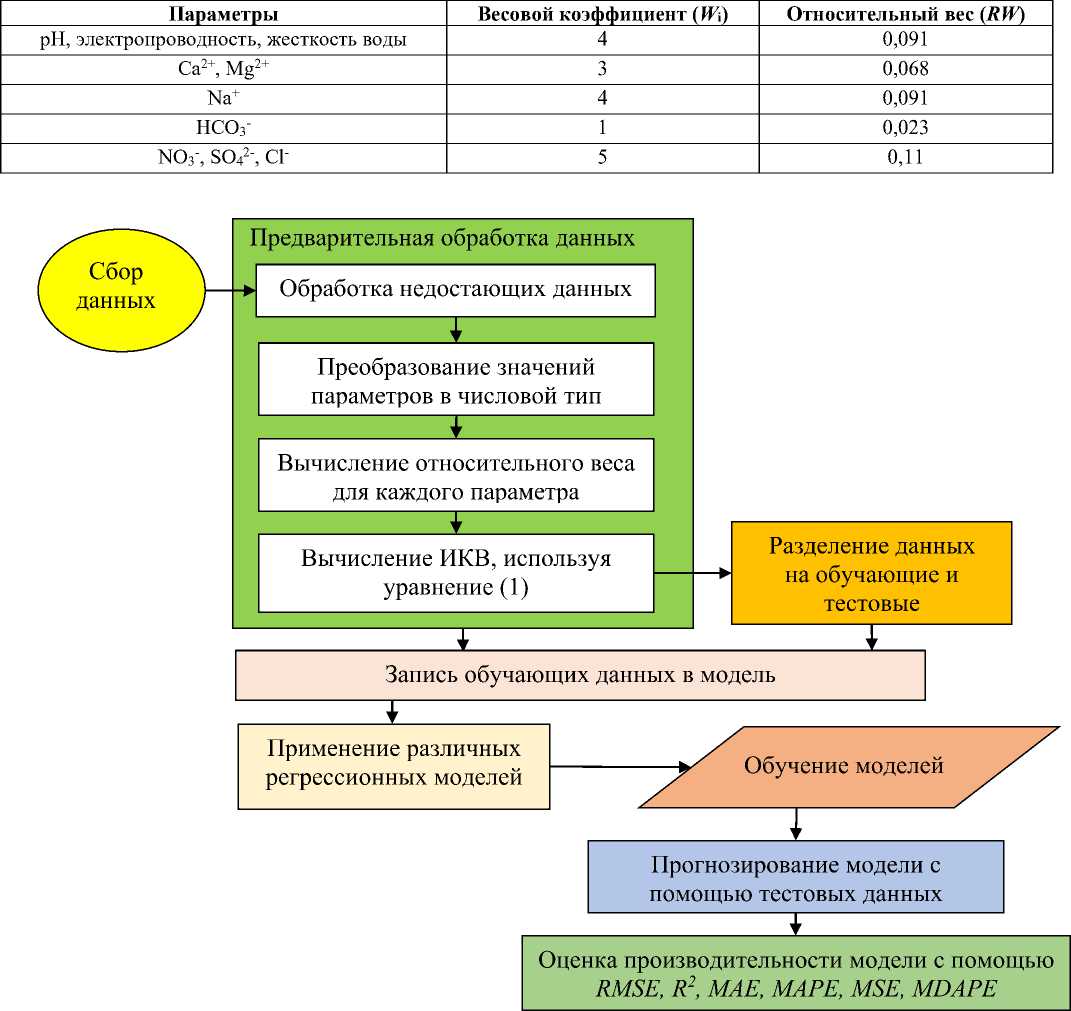
Рис. 3. Предлагаемая структура для прогнозирования индекса качества воды

как электропроводность, жесткость воды, Ca2+, Mg2+, Na+, HCO3-, NO3-, SO42- и Cl-. Для расчета индекса ка-частва воды, который измеряет качество грунтовых вод для орошения и потребления человеком используется уравнение

EN q xw

ИКВ =    'N'  ‘ ,               (1)

W где Wi – это весовой коэффициент, представляющий собой отношение между константой пропорциональности и стандартным значением параметра качества воды qi [13; 31]. Относительный вес (RW) показан в уравнении:

RW =

w

En  , i=1 w'

где S – стандартное значение i -го параметра качества воды по данным ВОЗ [3]. Табл. 1 показывает вес и относительный вес ( RW ) параметров качества воды.

Модели машинного обучения

Мы внедрили различные алгоритмы регрессии для прогнозирования индекса качества воды, как показано на рис. 3. В регрессионном анализе используются независимые переменные для описания взаимосвязи между целевыми и предикторными переменными.

Параметры качества воды

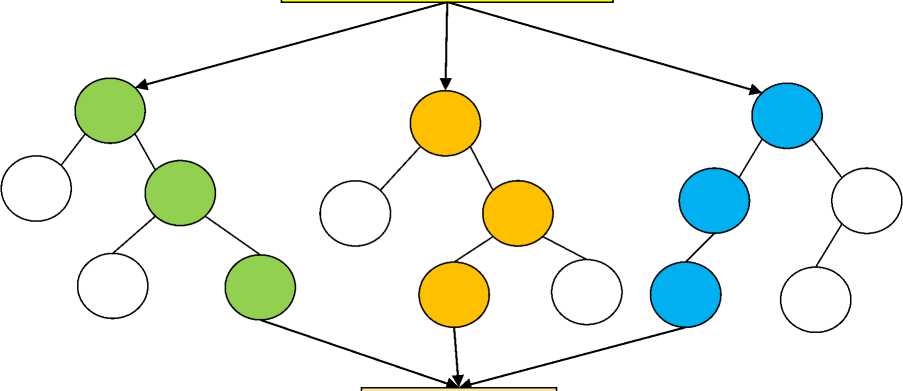
ИКВ

Рис. 4. Модель дерева решений для прогнозирования индекса качества воды

Линейная регрессия (ЛР)

Метод статистической регрессии, называемый линейной регрессией, используется в прогнозном анализе. Это один из простых алгоритмов, использующих регрессию для иллюстрации связи между непрерывными переменными. Алгоритм линейной регрессии использует независимую переменную V i и зависимую переменную V d [28]:

V d =Р о + P 1 V + ... + в n V„ ,              (3)

где значение точки пересечения Р_о и Р_; ( i =1, 2, .., n ) представляет собой коэффициенты параметров индекса качества воды; n – количество параметров равное 10.

Регрессия опорных векторов (РОВ)

В регрессии опорных векторов входной вектор для пространства x проецируется на многомерное пространство.    Этот    метод    выполняется    с соответствующей нелинейной функцией ядра, представленной символом f(x). Благодаря улучшенным методам оптимизации, которые можно использовать с различными переменными и ядрами, регрессия опорных векторов имеет положительную репутацию в плане эффективности прогнозирования.

Следующее уравнение представляет собой оценщик регрессии опорных векторов, где w действует как вектор весов, а b представляет смещения оценщика:

f РОВ = w ( x ) + b.               (4)

Регрессия XG Boost (XGB)

Алгоритм XG Boost основан на алгоритме повышения градиента. Двумя значительными улучшениями являются член регуляризации в его целевой функции, который делает ее менее склонной к переобучению, и использование целевой функции с уравнением Тейлора, которое позволяет XGB более точно определять функцию потерь [32].

Регрессор наименьшего угла (РНУ)

Регрессор наименьшего угла определяет связь между двумя атрибутами и движется в направлении, перпендикулярном атрибутам.

Регрессия Байесовского хребта (РБХ)

Регрессия Байесовского хребта, одна из наиболее практичных форм байесовской регрессии, вычисляет вероятностную модель проблемы регрессии. Формула коэффициента гребневой регрессии определяется с помощью квадрата величины коэффициента [24]:

Р хребет = min || У - X Р| |2 + X |в| |2 (5) с настраиваемым параметром X .

Случайный древовидный регрессор (СДР)

Древовидный регрессор использует несколько деревьев решений для выполнения задач регрессии и классификации, как показано на рис. 4.

Эластичный чистый регрессор (ЭЧР)

Лассо и хребет используются в линейной эластичной чистой регрессии для упорядочивания регрессионных моделей. Эта тактика сочетает в себе процедуры регрессии и лассо для улучшения регуляризации статистических моделей.

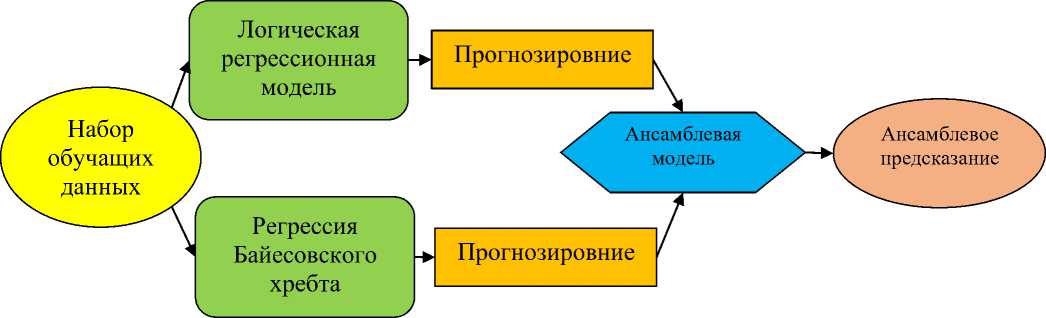
Рис. 5. Ансамблевая модель для прогнозирования индекса качества воды

Таблица 2

Показатели производительности с помощью анализа главных компонент

Методы МО	С анализом главных компонент
	RMSE	R2	MAE	MAPE	MSE	MDAPE
Линейная регрессия	0,87	0,9984	0,1739	0,0029	0,7605	0,1152
Регрессия опорных векторов	21,21	0,0757	9,4664	0,2475	450,14	10,0573
Регрессия XG Boost	2,08	0,991	1,5108	0,0345	4,3509	1,8831
Регрессор наименьшего угла	0,87	0,9984	0,1739	0,0295	0,7605	0,1152
Регрессия Байесовского хребта	0,87	0,9984	0,174	0,0029	0,7605	0,1151
Случайный древовидный регрессор	3,16	0,9794	2,4404	0,0587	10,0126	3,1838
Эластичный чистый регрессор	21,57	0,0444	17,5259	0,813	465,39	22,5727
Ансамблевая модель	0,31	0,9980	2,771	0,09	9,7687	4,878

Ансамблевая модель (АМ)

Еще одним популярным алгоритмом машинного обучения является ансамблевая модель. В ней различные модели машинного обучения объединяются для прогнозирования результата. В нашем исследовании байесовская и логическая регрессия (рис. 5) объединены для прогнозирования индекса качества воды, поскольку может оказаться, что две модели будут иметь более низкие значения RMSE .

Результаты и обсуждение

Результативность различных моделей

Различные модели машинного обучения, такие как линейная регрессия, регрессия опорных векторов, регрессия XG Boost , регрессия наименьшего угла, регрессия Байесовского хребта, случайный древовидный регрессор, элестичный чистый регрессор и ансамблевая модель, были применены к набору данных. Производительность каждой модели оценивается с использованием следующих показателей:

Корень от средней квадратичной ошибки ( RMSE ) =

У N ( i прогноз . - 1измер .)²

R 2=   „-----------------------;

• У, _t ( i измер . - i прогноз .)² Средне - квадратичная ошибка ( MSE ) =

• У N J i измер . - i прогноз .||²

N

;

Средняя абсолютная погрешность ( МАЕ ) = У N ||i прогноз . - i измер .| |

N

;

Средняя абсолютная погрешность в %( МАРЕ ) = У N 1| измер . - прогноз .||

N

;

Средняя абсолютная погрешность производительности ( MDAPE ) =

= средн .

У N ( измер . - прогноз .) измеренное

• 100.

/v¹ N и-                       2"

У   i измер . - 1 прогноз .

N

;

Показатели производительности, включая RMSE , R² , MAE , MAPE , MSE и MDAPE , были рассчитаны с использованием и без использования анализа главных компонент, соответственно, как показано в табл. 2 и 3. Ансамблевая модель превзошла другие модели и аналогичные исследования с точки зрения ошибки RMSE . Анализ главных компонент помогает в ин-

Линейная регрессия

Регрессия опорных векторов

Регрессия XG Boost

Регрессор наименьшего угла

Регрессия Байесовского хребта

Случайный древовидный регрессор

Эластичный чистый регрессор

Ансамблевая модель

Линейная регрессия

Регрессия опорных векторов

Регрессия XG Boost

Регрессор наименьшего угла

Регрессия Байесовского хребта

Эластичный чистый регрессор

Ансамблевая модель

д

Случайный древовидный регрессор

Линейная регрессия

Регрессия опорных векторов

Регрессия XG Boost

Регрессор наименьшего угла

Регрессия Байесовского хребта

Случайный древовидный регрессор

Эластичный чистый регрессор

Ансамблевая модель

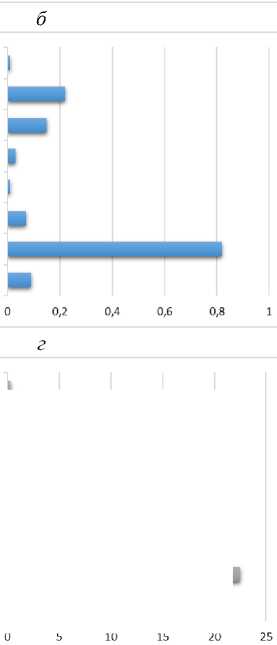
е

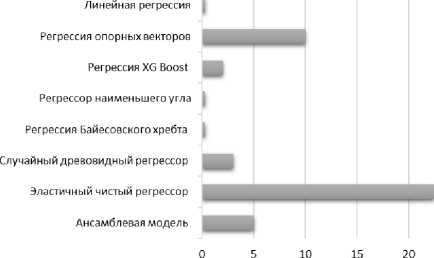
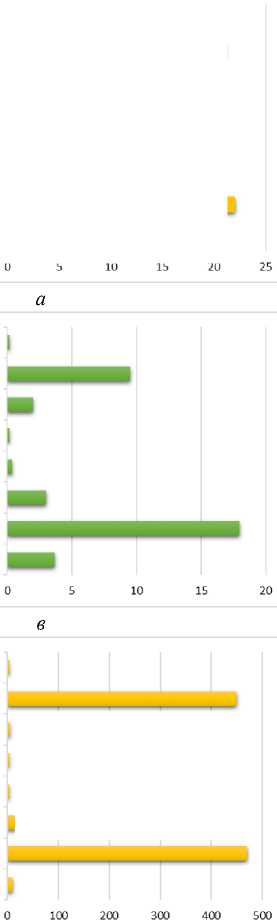
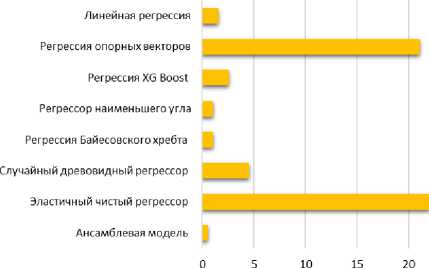
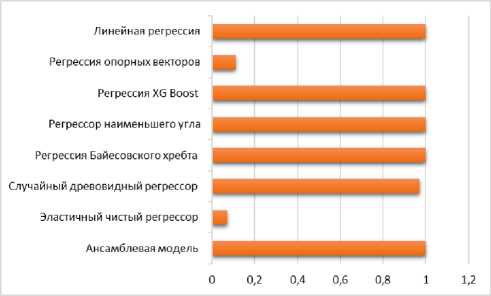
Рис. 6. Показатели производительности с анализом главных компонент: a – RMSE ; б – R² ; в – MAE ; г – MAPE ; д – MSE ; е – MDAP

Таблица 3

Методы машинного обучения	Без анализа главных компонент
	RMSE	R2	MAE	MAPE	MSE	MDAPE
Линейная регрессия	0,0000030	0,9999	0,0000024	0,00000004	9e^-12	0,0005
Регрессия опорных векторов	1,71	0,9936	0,9918	0,0513	2,92	0,79
Регрессия XG Boost	1,85	0,9925	1,3413	0,02543	3,42	1,46
Регрессор наименьшего угла	0,0000035	0,9666	0,0000026	0,00000004	8,41e^-12	0,0035
Регрессия Байесовского хребта	0,0000028	0,9999	0,0000024	0,00000004	7,84e^-12	0,0035
Случайный древовидный регрессор	3,6585	0,9708	2,4907	0,04974	13,38	2,7
Эластичный чистый регрессор	21,1777	0,0238	17,3209	0,05363	448,49	21,17
Ансамблевая модель	0,0000024	0,9999	0,0000022	0,00000004	0,0000033	0,0001

Таблица 4

Сравнительный анализ различных моделей машинного обучения для прогнозирования индекса качества воды

Ссылка	Модель	Параметры	Прогноз	RMSE
Лам Цуен, Гонконг [7]	Дополнительная древовидная регрессия	Биологическая потребность в кислороде, мутность, фосфаты	ИКВ	3,74
Водосбор Талара, Иран [9; 10]	Байесовские деревья аддитивной регрессии	Биологическая потребность в кислороде, мутность, фосфаты, pH, нитраты, электропроводность, растворенный кослород, химическая потребность в кислороде	ИКВ	2,71
Варта [19]	Искусственная нейросеть	Общая минерализация, жесткость воды, нитраты, марганец	ИКВ	0,62450
Деревня Сычик (17 вырытых колодцев) [28]	Искусственная нейросеть	CO, pH, Ca, Mg, и K, SO 4 2-	ИКВ	0,651258
Район Райпур, Чхаттисгарх, Индия [30]	Глубокое обучение	Общая минерализация, Ca2+, Mg2+, NO 3 ˉ и PO 4 3-	ИКВ	1,254
Предлагаемая работа	Ансамблевая модель (логическая и байесовская регрессия)	pH, электропроводимость, жесткость воды, Ca2+, Mg2+, Na+, HCO 3 -, NO 3 -, SO 4 2- и Cl-	ИКВ	0,00000286

Показатели производительности без анализа главных компонент

терпретации данных, хотя и не всегда выявляет значимые закономерности. На рис. 6 и 7 изображены показатели производительности в графическом виде.

Для преобразования многомерных данных в низкоразмерные данные часто используется анализ основных компонент (АОК). Многие коррелированные переменные в исходном наборе данных часто могут быть преобразованы в небольшое количество некоррелированных переменных [21; 25]. Хотя анализ основных показателей упрощает сложные многомерные данные, в этом исследовании все параметры качества грунтовых вод важны для определения индекса качества воды, и, следовательно, анализ основных показателей не дает лучших результатов.

В табл. 4 показан сравнительный анализ различных моделей машинного обучения для прогнозирования индекса качества воды. В [7] авторы исследовали эффективность дополнительной регрессии деревьев (ДРД) для прогнозирования индекса качества воды для реки Лам Тьюз и предложили среднеквадратичное отклонение 3,74 для комбинации входных параметров, таких как биологическая потребность в кислороде (БПК), мутность и концентрация фосфатов. Судхакару и соавт. [30] был сделан прогноз индекса качества воды на основе глубокого обучения для 226 проб грунтовых вод, взятых из Аранга округа Раджпур, Чхаттисгарх, Индия, и получено значение RMSE 1,254. В [18] модель искуственной нейросети применена к 17 вырытым колодцам, и получено значение RMSE 0,651258. Авторы [9] предложили гибридную модель байесовских деревьев аддитивной регрессии и получили RMSE 2,71. Авторы [19] использовались пять параметров, вместе с искусственной нейросетью для реки Варта в Польше. RMSE модели 0,62450. На рис. 8 показано значение RMSE, полученное исследователями с ис- пользованием различных моделей машинного обучения.

Классификация индекса качества грунтовых вод для штата Тамилнад

Ансамблевые модели в дальнейшем используются для классификации областей качества грунтовых вод в штате Тамилнад на основе индекса качества воды. В табл. 5 показан диапазон индекса качества воды и соответствующая ему отметка класса.

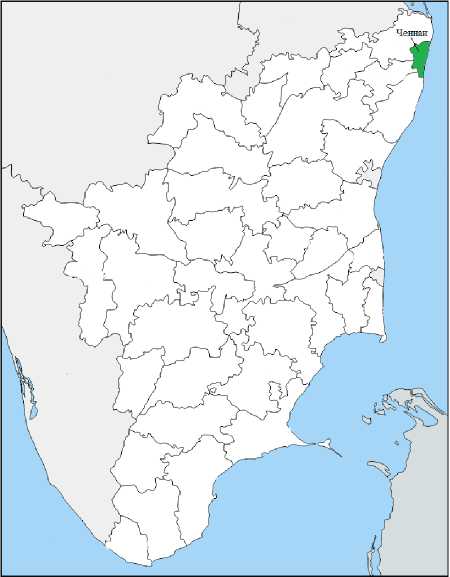
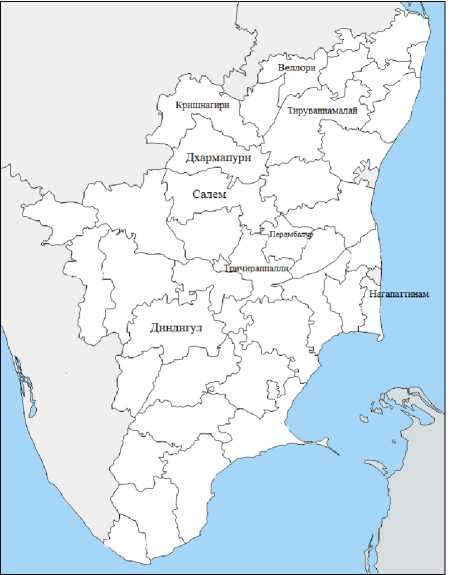
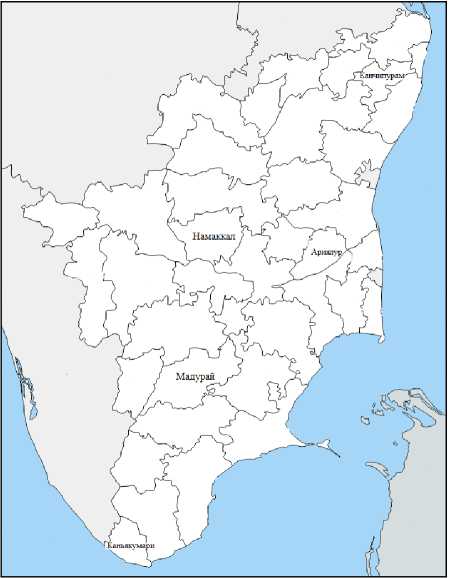
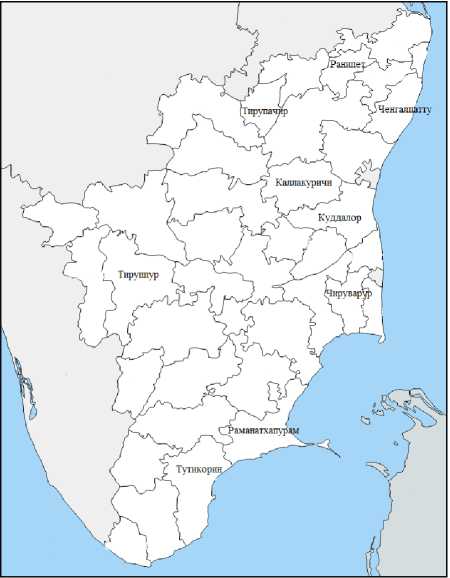
На рис. 9 показаны районы, в которых качество грунтовых вод находится в отличном и умеренном состоянии. Отмечено, что в некоторых частях Ченнаи грунтовые воды отличного качества с индексом качества воды ниже 25, а такие районы, как Кришнагири, Салем, Дхармапури, Тируваннамалай, Тричи, Динди-гул и Нагапаттинам, попадают под категорию умеренного качества. На рис. 10 показано, что Канчипурам, Намаккал, Каньякумари и Мадурай относятся к категории хороших по индексу качества воды, а такие районы, как Тутикорин, Раманатхапурам, Куддалор и Ченгалпатту, относятся к категории плохих соответственно. Это показатели качества грунтовых вод с использованием индекса качества воды в различных местах штата Тамилнад.

На рис. 11 показаны районы, попадающие в категорию «очень плохо» по индексу качества воды. К этой категории относятся районы Тирунвелели, Тен-каси, Вирудхунагар, Тени, Шивагангай, Пудукоттай, Коимбатур, Нилгирис, Эроде и Виллупурам.

В табл. 6 показаны показатели производительности для ансамблевой модели. Замечено, что для графика, соответствующего категории «отлично», получена точность 96%. Значение точности составляет 96% и для классификации округа «хорошо», обнаружено, что

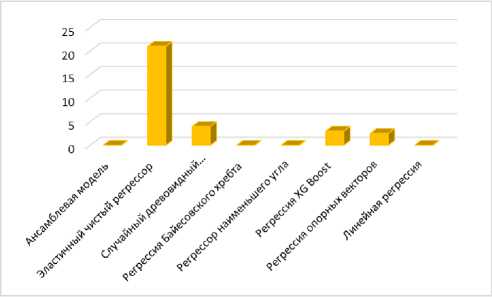
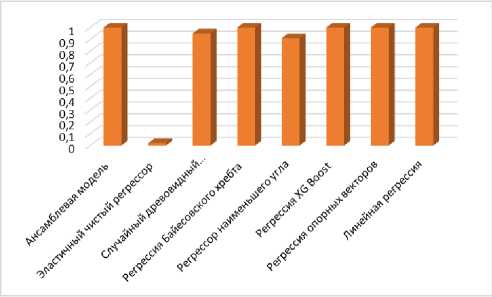
б

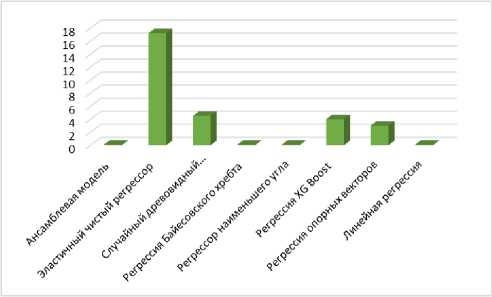
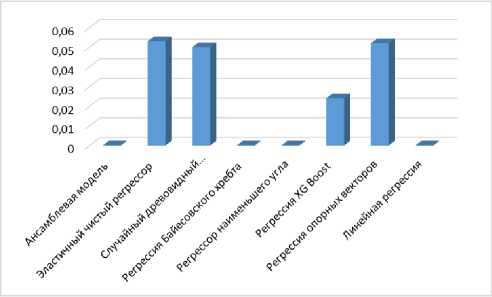
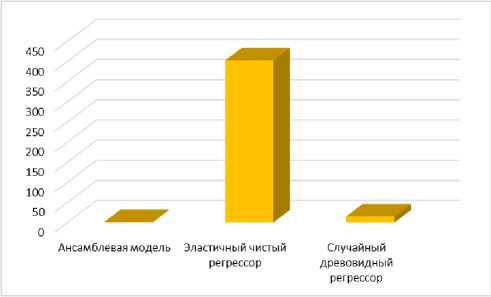
Рис. 7. Показатели производительности без

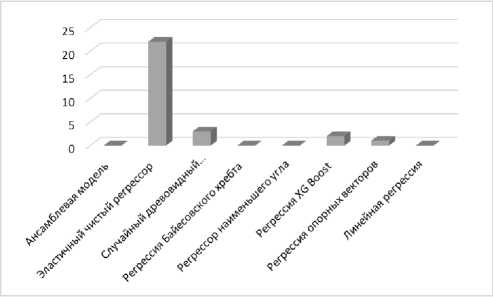
е анализа главных компонент: a – RMSE; б – R2;

в – MAE ; г – MAPE; д – MSE ; е – MDAPE

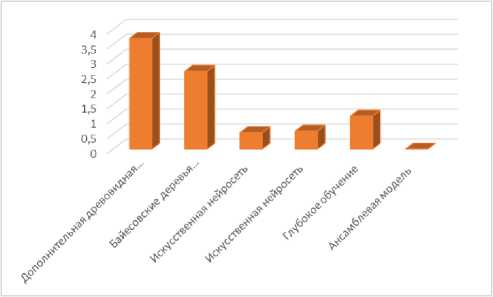
Рис. 8. Значения RMSE , заданные различными моделями машинного обучения

Таблица 5

Диапазон значений и отметок индекса качества воды

№ п/п	Оценка ИКВ	Качество грунтовых вод
1	<25	отлично
2	26–50	хорошо
3	51–60	умеренно
4	61–75	плохо
5	76–100	очень плохо

а                                                       б

Рис. 9. Районы, относящиеся к категориям: а – отлично; б – умеренно по качеству грунтовых вод

а                                                       б

Рис. 10. Районы, относящиеся к категориям: а – хорошо; б – плохо по качеству грунтовых вод

Таблица 6

Определение метрик для классификации ансамблевой модели

Категория Точность Прецизионость Отзыв F1-оценка Отлично 0,96 0,96 1,00 0,98 Хорошо 0,96 0,97 0,92 0,94 Умеренно 0,96 0,94 0,96 0,95 Плохо 0,96 0,94 0,94 0,94 Очень плохо 0,96 0,96 0,95 0,95 отзыв и оценка F1 максимальны для классификации «отлично».

Заключение

В этом исследовании восемь моделей машинного обучения использовались для прогнозирования качества грунтовых вод на основе индекса качества воды. Модели проверяются с использованием показателей качества, таких как RMSE , R² , MAE , MAPE , MSE и MDAPE . Замечено, что ансамблевая модель дала наименьшую среднеквадратичную ошибку порядка 2,8 ⋅ 10 ^{- 6} во время тестирования. Отмечено, что ошибка меньше по, сравнению с другими моделями и другими предыдущими исследованиями. Модель будет полезна для прогнозирования ряда дополнительных биохимических и физико-химических характеристик грунтовых вод используемых для питья. Результаты этого исследования могут быть усилены путем сравнения производительности моделей машинного обучения с моделью Deep с учетом различных входных гидрохимических параметров. Далее ансамблевая модель используется для классификации областей на основе значений индекса качества воды.

River water quality index prediction and uncertainty analysis: A comparative study of machine learning models // Journal of Environmental Chemical. – 2021. – Vol. 9, No. 3 –

P. 105–109.

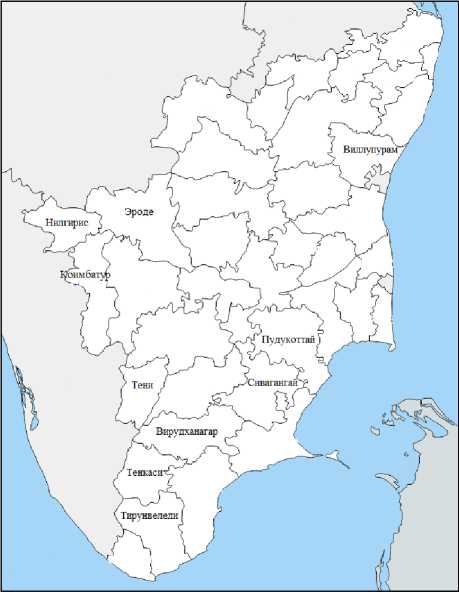
Рис. 11. Районы, относящиеся к категории «очень плохо» по качеству грунтовых вод

Artificial neural network modeling of the water quality index for Kinta River (Malaysia) using water quality variables as predictors // The Marine Pollution Bulletin. – 2012. –

Vol. 64. – Р. 2409–2420.