Прогнозирование ключевых показателей розничной сети во времени

Большое количество проведенных исследований по управлению товарными запасами, реа- лизации маркетинговой политики, стратегическому планированию в сфере розничной торговли посвящено адекватному прогнозированию спроса на товар. Значимость прогнозирования является неоспоримой, тем более в период бурного роста данных о состоянии экономики и иных сфер жизни современного общества. Необходимо подходить комплексно к анализу существующей на предприятии системы управления запа- сами, к оценке состояния информационных систем, наличия необходимых данных, а также к выявлению состава факторов, влияющих на спрос на тот или иной товар.

Ранее проведенное исследование [1] позволило выделить ряд ключевых факторов, влияющих на спрос. Поэтому их включение как показателя в математическую модель спроса является обоснованным решением и увеличивает точность получаемого результата. Однако здесь возникает важное обстоятельство: при прогнозировании спроса на конкретный товар лицо, принимающее решение, не может знать будущих показате- лей для ряда факторов, которые являются ключевыми. Следовательно, для расчета прогноза спроса на товар необходимо рассчитать прогноз ключевого (экзогенного) фактора, включенного в основную модель. От точности модели прогнозирования фактора зависит точность всей системы прогнозирования в целом. Данный подход актуален для исследования особенностей функционирования сложных экономических и технических систем, в настоящем исследовании – в системе товародвижения в розничной торговле.

Описан процесс построения моделей прогнозирования для двух основных факторов, которые влияют на покупательский спрос, – эндогенный ключевой показатель по отношению к работе розничного предприятия (количество покупателей (чеков) в магазине) и экзогенный (температурный режим). Их использование обусловлено высокой степенью значимости влияния показателей на работу торговой сети. Количество чеков – это формальный показатель эффективности магазина, температурный режим – показатель, который чаще всего влияет на размер покупательского потока и спрос на конкретные виды товаров. Конечно, каждый из этих показателей имеет уникальную природу и к каждому необходимо подходить, используя разные теоретические и практические основания. Но для их прогнозирования будет использоваться единый инструментарий анализа временных рядов, в том числе современные наработки в этой области. Будет проведен сравнительный анализ методов прогнозирования для каждого из интересующих нас факторов, выявлена лучшая модель с точки зрения установленного показателя качества и сделаны выводы о прогностической способности каждой модели. Рассматриваемые модели могут использоваться, как было сказано выше, как в общем комплексе системы прогнозирования товарного спроса на предприятии розничной торговли, так и независимо – для составления необходимых планов и для выработки необходимых тактических мер. Это обусловлено тем, что рассматриваемые показатели несут значимую информацию сами по себе: корректное предсказание тем- пературного режима позволяет регулировать ценообразование по некоторым видам товаров, а количество и динамика чеков сообщают о результатах проведенных маркетинговых мер.

Основным направлением исследования является построение методологии ключевых показателей, определяющих структуру спроса в розничной торговле. Для решения этой задачи будет использован инструментарий анализа временных рядов.

Методы исследования временных рядов

И сходя из характера переменных, можно отметить, что при прогнозировании должны применяться методы анализа временных рядов с четко выраженной сезонностью. При этом состав методов будет определен современными теоретическими и практическими достижениями в этой области.

Для прогнозирования временных рядов в настоящем исследовании будут использоваться:

• -    модель экспоненциального сглаживания, которая традиционно используется в прогнозировании временных рядов так же, как и ARIMA;

• -    ARIMA-моделирование, реализованное с помощью алгоритма Хиндмана – Хандакара [2];

• -    модель комплекснозначного экспоненциального сглаживания, представляющая одну из современных разработок в области анализа временных рядов [3; 4];

• -    вычислительный       продукт

Prophet,     разработанный     компанией

Facebook. По сути, данный алгоритм является аддитивной регрессионной моделью с определенным набором дополнительных факторов для вычисления сезонности и учета кратковременных важных изменений (праздников) [5];

• -    байесовские структурные временные ряды, являющиеся сочетанием нескольких подходов к анализу временных рядов, основанных на теории Байеса. Метод дорабатывается и используется для прогнозирования компанией Google [6].

Большой набор используемых методов объясняется тем, что результатом исследования может являться не просто выбор лучшего метода, но и построение их сочетания в случае целесообразности данного решения. Перед тем как приступить к описанию проведенных расчетов, в краткой форме опишем теоретические предпосылки выстраиваемых алгоритмов.

Модель экспоненциального сглаживания (ETS)

В настоящее время модели экспоненциального сглаживания разной спецификации и интегрированная модель авторегрессии – скользящего среднего (ARIMA) – наиболее популярные инструменты для прогнозирования временных рядов. Оценить классификацию и значение классических временных рядов можно в работе [7].

Идею экспоненциального сглаживания отражает самая простая спецификация – модель простого экспоненциального сглаживания:

y t = ay t-1 + ⁽1 - a)y t-i , (1) где y_t - прогнозируемое значение временного ряда в момент t, y_t-1 - фактическое значение временного ряда в момент t — 1, а -параметр сглаживания, принимающий значения от 0 до 1. Следовательно, речь идет о процедуре «сглаживания» исходного ряда, которая позволяет увидеть изменения в тенденциях. В развернутых спецификациях оцениваются и другие возможные компоненты – сезонности и ошибки.

В нашем исследовании модели экспоненциального сглаживания строятся с помощью математической модели пространства состояний. Метод пространства состояний используется достаточно часто на практике, в том числе для математического моделирования систем, поскольку задает составляющие исследуемого объекта, которые функционируют самостоятельно [8]. Это означает, что у нас есть 30 вариаций моделей экпоненциального сглаживания, каждая из которых содержит три компоненты – ошибка, тренд и сезонность, или (E,T,S). В состав моделей входит, например, часто используемая в анализе временных рядов модель Хольта – Винтерса. В пространстве мо- делей существует два глобальных класса. Первый – модели аддитивные, которые имеют следующую форму:

fyt = ^Vt-i + et                       (2)

Ivt = Fvt—i + get где yt - фактическое значение временного ряда в момент t, vt - вектор состояний, который содержит в себе компоненты (E,T,S), ш- заданный измерительный вектор, F - матрица переходов, g - вектор, который содержит в себе постоянные сглаживания и et - ошибка модели, распределенная нормально.

Второй класс – мультипликативные модели – описывается с помощью логарифмов аналогично предыдущей форме:

(y t = ^ех Р ^(ш' logO t-i ) ⁺ log(l + ^et))

I log(v t ) = Flog(v t-i ) + log(1 + ge t )

В данном случае ошибка 1 + et распределена логнормально.

Выбор лучшей модели из пространства осуществляется с помощью информационных критериев: используется информационный критерий Акаике, который для класса данных моделей выражен в следующей формуле:

AIC = —2 log(L) + 2к,                (4)

где L - максимизированное значение функции правдоподобия модели, к - общее количество параметров модели. Выбор модели осуществляется по наибольшему значению информационного критерия.

Модель авторегрессии – скользящего среднего (ARIMA)

Модель ARIMA имеет стандартную спецификацию вида yt = с + a^t-i +■■■ +apyt-p+ +P1et-1 +-----+ ^qet-q + et, где yt-1,..., yt-p - предыдущие фактические значения временного ряда, сдвинутые от фактического на лаг от 1 до р, et-1, ..,et-q – предыдущие ошибки модели, сдвинутые от фактической на лаг от 1 до q,c - константа модели^ - прогнозное значение временного ряда.

По сути, ARIMA-моделирование заключается в корректном подборе спецификации модели ARIMA(p, d, q), где d - порядок разности временного ряда, при котором ряд для соответствующих разностей оказывается стационарным. Часто поиск корректной спецификации модели является трудоемкой и нетривиальной задачей. И в целях автоматизации данной рутинной процедуры существует алгоритм Хиндмана – Хандака-ра. Обобщенно, алгоритм является иттера-ционной процедурой, которая, изменяя параметры модели р, d и q, минимизирует значение скорректированного информационного критерия Акаике.

Информационный критерий Акаике и скорректированный информационный критерий Акаике для ARIMA характеризуются следующими формулами:

AIC = —2 log(L) + 2(р + q + к + 1),

AIC_c = AIC +

2(р + q + к + 1)(р + q + к + 2)(7)

+      Т — р — q — к — 2, где L - максимизированное значение функции правдоподобия модели; к = 1, если константа по модели с Ф 0 и к = 1, если верно обратное. Данный информационный критерий разработан и используется для выбора лучшей из нескольких статистических моделей.

Соответственно, для всех ARIMA-моделей в данном исследовании используется алгоритм Хиндмана – Хандакара как инструмент минимизации издержек на создание прогнозной системы. Для отражения определенных эффектов в ARIMA-моделировании также используются дополнительные регрессоры. Вид изначальной функции меняется на следующий: y_t = c + a₁y_t - ₁ + - + a_py_t - _p + ⁺ P 1^et-1 + -----+ ^ q^et-q ⁺                    (8)

+^ i % i + — + Ш к Х к + e t , где X 1 ,^,X k - дополнительные регрессоры, введенные в модель. Здесь могут быть использованы разные наборы признаков для улучшения качества прогноза. Это может быть, например, наличие праздника, ряды Фурье для отражения сезонности и многое другое в зависимости от контекста задачи.

Если оценивать прикладной характер метода, то ARIMA является одним из наиболее часто используемых инструментов анализа временных рядов, в том числе, например, при прогнозировании самого то- варного спроса, что можно увидеть в работе [9].

Модель комплекснозначного экспоненциального сглаживания (CES)

Модель комплекснозначного экспоненциального сглаживания берет в свою основу понятие комплексного числа X + iy, где X и у - числа на вещественной прямой, а i - мнимая единица (i ² = —1).

В теории, для строгого определения принципов моделирования, вводится понятие «информационный потенциал» р_t как ненаблюдаемая составляющая временного ряда, влияющую на состояние видимых значений y_t . Две вещественные переменные объединяются в одну комплексную y_t + iр_t . Соответственно, общий процесс описывается следующей функциональной формой: y t + iP t = Ш, ej,                    ⁽⁹⁾

где Q - множество комплексных значений, выбранных для моделирования комплексной переменной y_t + iр_t .

Объединяя идею информационного потенциала и простую модель экспоненциального сглаживания, приходим к следующей формуле:

^yt+1 ^{+ iр}t+1 = ^(ao ^{+ ia}1⁾⁽ y t ^{+ i} P t^{) +} + ⁽ 1 — a o + i — ia^ t + iр_t ⁾ , где y_t - прогнозная оценка временного ряда, р_t - оценка значения информационного потенциала, a₀ + ia 1 - комплексный параметр сглаживания.

Так же, как и модель экспоненциального сглаживания, комплекснозначное экспоненциальное сглаживание имеет базовую статистическую модель пространства состояний. Ее форма выражена в следующем виде:

y t = l t-1 ^{+ e}t

I t = l t-1 — (1 — a 1 )C t-1 — a 1 P t + a_oe_t,  (11)

^ct = ^lt-1

где y_t - фактическое значение временного ряда, l_t - уровень временного ряда, c_t - информационная компонента при наблюдении в момент t. В компактной форме это можно записать следующим образом:

С    y t = ш v_t-1 + ^et

I V t = Fv t-1 + qр t + ge t

Видно, что форма аналогична форме экпоненциального сглаживания (2).

Модель Prophet

В отличие от модели экспоненциального сглаживания и ARIMA-моделирования алгоритм, реализованный в системе Prophet, имеет другое теоретическое основание. В теории модель, которая легла в основу Prophet, раскладывается на ряд компонент: $ t = g t + s t + h t + ^et ,                  ⁽¹³⁾

где g_t - трендовая компонента, s_t - сезонная компонента и h_t - компонента, которая отражает в себе информацию по праздничным периодам и другим нерегулярным событиям.

По сути, алгоритм работает подобно обобщенной линейной модели, общая спецификация которой выражена следующим образом:

д(Е(У)) = ^ o +f i (x i ) +            (14

+ ^f2^(x2 ) +-----+ f m^(xm ).

Формула (14) своим видом напоминает стандартную множественную линейную регрессию, но основное ее отличие состоит в замене стандартных линейных компонент P j X ij на нелинейную функцию f j от аргумента X ij [10]. Это означает, что трендовая составляющая,^ является суммой функций от временных промежутков, которые настраиваются либо вручную исследователем, либо автоматически при определении точек изменения тренда и величины изменения скорости тренда в этот момент - (s j , 8 j ) При этом в рамках данной статьи мы используем кусочно-линейную трендовую компоненту g_t.

Для моделирования сезонной компоненты s_t используютсяследующие процедуры:

• 1)    для определения существующей годовой сезонности применяются ряды Фурье;

• 2)    для описания существующей недельной сезонности используются фиктивные переменные.

Компонента ht определяется с помощью индикаторной переменной для каждого праздника (или значимого дня). В том случае если изменения целевой переменной yt, приуроченные к конкретному празднику, имеют место быть в некотором диапазоне дней длиной L, то данный диапазон считает- ся        указанным        праздником:

Z(tlte [tk;tk+L\) = 1.

Для оценки модели используется один из итерационных методов численной оптимизации второго порядка – алгоритм Бройдена – Флетчера – Гольдфарба – Шанно или BFGS-алгоритм [11, с. 391–392].

Байесовская структурная модель временных рядов (BSTS)

Байесовский подход к решению задач как статистики, так и эконометрики значительно отличается от подхода классической теории вероятностей. Главным образом, особенность подхода состоит в том, что вероятность события определяется в первую очередь наполненностью информации о рассматриваемом явлении. Это дает большое преимущество по сравнению с положениями классической теории – уже на малых выборках возможно делать выводы о явлении, уточняя вероятность исходов по мере появления новой информации [12].

Байесовские структурные временные ряды – еще один метод анализа временных рядов, который можно отнести к моделям пространства состояний. При этом он сочетает в себе инструменты байесовского подхода, развитые на текущий период. Моделирование состоит из трех основных этапов:

• 1.    Применение фильтра Калмана.

• 2.    « Spike-and-slab » метод выбора переменных (метод имеет малую распространённость в русскоязычных научных источниках, поэтому в данной статье используется оригинальное название).

• 3.    Байесовская модель усреднения.

Ввиду достаточной сложности в данной статье алгоритм не приводится в полной формулировке. Наиболее подробно байесовский подход к прогнозированию временных рядов описан в теоретической работе [13]. Здесь приведены несколько общих понятий и характеристика методов, а также последовательность их применения для выхода на нужный результат.

В данном случае структурная модель временного ряда определяется следующим образом:

y_t = Z [ a_t + е

• ^{t t t t} ,                                (15)

»t+i = Ttat + Rt^t где yt - значения ряда, a t - скрытая переменная состояния. Матрицы Zt, Tt и Rt характеризуют известные и неизвестные параметры, оцениваемые в модели. Как видно, структура похожа на аналогичные формы, приведенные для моделей экспоненциального сглаживания.

Обычно для работы с моделями пространства состояний применяют фильтр Калмана [14]. Фильтр рекурсивно рассчитывает прогнозное распределение f (a_t+i \y_i:t), объединяя f(^tlyi:t—i) вместе с y_t , при этом используя стандартный набор формул, который логически сводится к алгоритму линейной регрессии. Процедура сглаживания Калмана преобразует выходные значения фильтра для получения распределения f( ^a t\y_1: n ), где ^п -количество элементов во временном ряде для каждого момента t. Так как по предпосылкам модели все составляющие имеют гауссовскую природу, то fMy i-.t-i ) и f ⁽ a_t\y i: _n) - это многомерные нормальные распределения со средней ^_t и дисперсией D_t . Фильтр Калмана собирает информацию о временных рядах по мере итеративного движения по списку пар (^_t. D t ). Сглаживание Калмана используется для распределения информации о более поздних наблюдениях последовательно по более ранним парам (^_t. D_t).

Идея « spike-and-slab » заключается в том, чтобы снизить количество подаваемых на вход структурной модели признаков. Для реализации метода вводятся несколько специальных обозначений: у_к = 1, если Р к ^ 0 и Y k = 0, если Р к = 0, где Р к - коэффициенты при регрессионных признаках. Обозначают также P y как пространство коэффициентов Р, где р_к ^ 0. «Spike-and-slab » подход выражен в оценке априорного вероятностного распределения:

= P i (P y \ Y, °2)P 2tee \ Y)P 3⁽ Y). ^{

Маргинальное распределение p₃(y) задается с использованием распределения Бернулли:

V-П к - ^ k ^k \ _я ,)' ■-. (17)

Уравнение (17) можно упростить, о чем подробно сказано в работе [15].

Дальнейшие обозначения, определяющие строки и столбцы матрицы, -Q- ⁱ для симметричной матрицы a ^-i , где Y k = 1. Тогда условные априорные распределения f(1/a ² \Y') и f(P_y\o_e.Y) могут быть выражены условной сопряженной парой: P_y\ ⁽ ^ e >Y)~R (b_y,^²(^ y ⁱ) ⁱ), i         V ss                               ⁽¹⁸⁾

^2\y~g{2’T)’

где G(r,s) - гамма-распределение со средним r/s и дисперсией r/s ² .

Определяется уравнение   yt = yt — ZtTat, где Zt- матрица наблюдений структурной модели с PTxt, равным 0 (здесь и далее xtи X - признаки, определенные алгебраически и матрично). Также определяется у* = yt:n, где у*- этоубез компоненты временного ряда.

Совместное апостериорное распределение по Р и &£, условное по Y, доступно по следующим формулам:

P y \e e ,Y,y ^t ~N(fi y ,° ² (y y ^-i) ⁱ ),

(19) ^\Y.y - ~ ^G { 2 .^S{).

где достаточные статистики могут быть записаны в следующем виде:

v-¹ = (x ^T x) y + a ^-1 ,

Р у = (У у-уЧ х⁷’/-+ a^b y ) ,

N = v + п,                          (20)

sS y = ss + у *Т у * + b y a -^ b y —

• -P^P y .

По причине сопряженности, можно маргинализировать по величинам P y и 1/0 2 , чтобы получить

\a ^-i \² f(Y)

• Y\y * ~C(y * )   ^y т¹^ .             (21)

IVy-^ssy- где C(y*) - нормализированная константа, которая зависит от y*, но не зависит от Y.

Далее совокупность всех параметров модели, за исключением Р и 0 2 . обозначается через 9. Апостериорное распределение модели, которое описано выше, оценивают с помощью цепей Маркова методом Монте-Карло [11, с. 506–509]. Сам алгоритм разбивается на следующие шаги:

• 1.    Симуляция латентного уровня а из /(а|у,0,^,ст_е ² )с использованием метода на основе фильтра Калмана, описанного в работе [15].

• 2.    Симуляция 9 ~f (0|у, а, ^, ff_e ² ).

• 3.    Симуляция итоговых параметров Р и о % с помощью цепей Маркова со стационарным распределением f(p,a ^ ² ly,a,9).

Таким образом, прогнозирование временного ряда осуществляется на основа- нии оцененного апостериорного распределения, что соответствует парадигме байе- совского вывода.

Ряды Фурье (FS)

Ключевой теоретической предпосылкой, позволяющей с некоторым приближе- нием моделировать сезонность, является применение рядов Фурье в качестве независимой переменной практически во всех описанных выше методах. Обоснованность применения метода в данном качестве обу- словлена не только аналитически в рамках данной статьи, но и во многих других источниках. К примеру, ряды Фурье применя- ются для прогнозирования в технических сферах: в моделировании показателей надежности авиационной техники [16], в математической формализации технического состояния зданий [17] и мн. др. Также широко применение в задачах эконометри- ческого прогнозирования: как прогноз продаж [18], так и для оптимизации поставок [19]. Ограничимся кратким описанием идеи этого метода.

Использование рядов Фурье является частью спектрального анализа. Суть этого анализа состоит в том, чтобы представить временной ряд как сумму определенного оценка параметров ап и bn с помощью метода наименьших квадратов. Для решения задачи прогнозирования ключевых показателей, при использовании рядов Фурье, важно регулировать параметр к для получения качественного результата.

Метрика качества прогнозной модели

Для оценки качества применяемых методов в первую очередь исходный ряд разделяется на обучающий и тестовый: на обучающем отрезке рассчитывается модель, на тестовом - вычисляется заданный показатель качества. В случае с рассматриваемыми факторами требуется краткосрочное прогнозирование на срок не более 14–21 дня. Это значит, что, учитывая длину временных рядов за 8 лет, допустимо разбить обучающую и тестовую выборки в соотношении 9 к 1. При частом регулярном пересчете параметров модели подобный подход является оправданным.

Очень важным вопросом при моделировании процессов является выбор функционала, который следует минимизировать или максимизировать в зависимости от контекста задачи. Так как в данном случае речь идет о прогнозировании, необходимо рассмотреть существующий функционал для задач прогнозирования. Наиболее популярные и простые функционалы - это метрики качества прогнозов, основанные на отклонении прогнозного значения от фактического: (У — У). Ввиду того, что исследуются показатели временных рядов с достаточно одно- значным течением процесса, то применяются именно простейшие методы оценки качества [20]. Кроме того, большая часть мето- вида частот, называемых гармониками: к

дов, рассмотренных выше, основаны на этих

^yt = «о

+

У (ап cos nt + bn sin nt),

n=1

принципах при расчете модельных параметров. Соответственно в нашем исследовании принято решение выбрать за основную мет-

где t - является характеристикой периода временного ряда в виде значений длины единичной окружности (например, для 12месячной сезонности значение для января t = 0, для декабря t = 11я/6), к определяется количество членов в частичной сумме ряда. По сути, здесь решается регрессионная задача для заданного вида Фурье-функции и

рику качества корень квадратный от средне-

квадратической ошибки модели (RMSE):

RMSE =

(yt

n

—

y t ) ²

где y_t - прогноз целевой переменной, y_t -фактическое значение целевой переменной,

n - количество дней в тестовом периоде,

RMSE - корень квадратный от среднеквадратической ошибки модели в тестовом пе-

риоде.

В качестве дополнительной метрики для оценки качества выбирается средняя абсолютная ошибка в процентах (МАРЕ ):

П

МАРЕ =1^

t=i

y t

—

yt

y t

х 100%

Эти две метрики позволяют объективно оценить точность модели на тестовой

выборке и сравнить используемые методы. Кроме того, каждая из предложенных метрик позволяет интуитивно оценить ошибку моделей и сделать выводы о ее качестве.

Таким образом, описаны основные

инструменты, с помощью которых производится прогнозирование ключевых переменных, оказывающих влияние на работу розничного сектора. Среди них как классические методы, применяемые на практике, так и новые методы анализа временных данных, которые стоит использовать для решения указанной задачи, одновременно тестируя их на эффективность. Тестирование проходит с помощью оценки метрик качества, на основе которых можно сделать выводы о точности методов. В следующем разделе приведены результаты прогнозирования показателей и оценка эффективности моделей.

Результаты исследования

П редставим результаты расчетов прогноза ключевых показателей с помощью моделей анализа временных рядов, способных обоснованно аппроксимировать такие важные показатели для ритейла, как температурный режим и количество чеков.

Температурный режим: анализ и прогнозирование

Влияние температурного режима на работу розничной торговли является очевидным, особенно для товаров повседневного спроса. Погодные условия влияют как на характер, так и на интенсивность покупок. Четкая сезонность спроса по многим видам товаров выделяется не столько по категориям «зима», «весна», «лето» и «осень»,

сколько по конкретным проявлениям погоды. Например, в жару употребляют больше освежающих напитков, в холодную погоду

летом покупательский поток ограничен для магазинов на окраине города и т.п.

Прогнозирование погодных условий, в том числе температурного режима, – в достаточной степени изученная научнопрактическая задача [21]. Поэтому при разработке системы прогнозирования товарного спроса целесообразно использовать данные из специальных сервисов по прогнозированию погоды – «Яндекс. Погода», «Google. Погода», «rp5» и др. Подобные сервисы имеют открытый API (англ. application programming interface – «программный интерфейс приложения»), достаточно просто интегрируются с внутренними системами предприятия. Тем не менее существуют некоторые ограничения в их применении:

1. Достоверность прогноза погоды может быть обеспечена только на ограниченное количество дней вперед (например, для Яндекса – до 10 дней). Поскольку цикл заказа может превышать установленные ограничения, это может быть проблемой при прогнозировании спроса.

2. Использование внешних систем может привести к дестабилизации информационной системы предприятия в том случае, если внешний сервис будет какое-то время неисправен.

Поэтому представляется целесообразным строить внутренний прогноз температурного режима, используя описанный инструментарий анализа временных рядов. Это позволит учитывать стабильные тенденции, которые существуют при изменении температурного режима на рассматриваемой местности.

Для временного ряда температур действует несколько предположений:

- имеет место четкая годовая сезонность – это является главной компонентой при прогнозировании;

- ряд имеет сигмоидальную структуру, что позволяет успешно использовать ряды Фурье в качестве дополнительных предикторов.

Для построения прогнозов используется выборка ежедневных средних температур в районе города Ижевска на основании

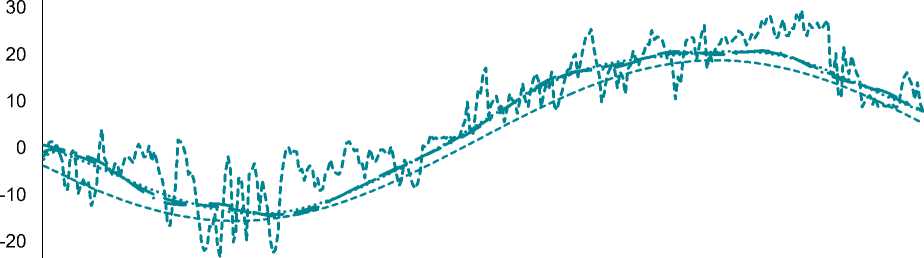
данных, полученных от метеостанций. Ниже приведен график прогнозов на тестовой выборке по трем методам прогнозирования, средний прогноз по двум лучшим методам и фактические значения температур (рис. 1).

-30

co co co co co co co co co T— T— T— T— T— T— T— T— T— ooooooooo СЧСМСЧСМСЧСМСЧСЧСМ oioicdcdxf^ininin ooooooooo |<^ЮОс6|<^1ЛО OCNOCNO-t-O-t-CN oooooooo т— т— т— т— т— т— т— т— oooooooo СЧСМСЧСМСЧСЧСЧСЧ oor^r^ododoo oooooooo Nocd^hC-r^^fod ■^СМ'^СМОСМО'Г-

Факт           Prophet

ARIMA ETS

Mean (Prophet, ARIMA)

Рис. 1. Динамика средних температур с прогнозами

Выбор только трех методов прогнозирования из представленных обусловлен избыточностью применения каких-то продвинутых методов прогнозирования погодных условий, если в наличии есть информация только по временному ряду средней температуры. При этом более серьезный подход для данной задачи ресурсозатратен, так как решается проблема управления торговым предприятием.

Приведем таблицу с основными метриками прогнозов (табл. 1).

Таблица 1

Результат тестирования методов прогнозирования для температурного режима

Метрика качества	Prophet	ARIMA	ETS	Mean (Prophet, ARIMA)
RMSE	5,60	5,36	6,85	5,46
МАРЕ, %	201,52	195,49	275,41	197,95

В табл. 1 показана значимость выбора метрики для выявления наиболее эффективного алгоритма прогнозирования. Метрика МАРЕ показывает себя не лучшим образом, так как исходный временной ряд имеет как положительные, так и отрицательные значения. В случае расчета МАРЕ, если разность yt — yt делится на фактическое значение yt ^ 0, то даже при не столь значительных отклонениях получаем значительное возрастание отношения (yt — —yt)/yt • Поэтому при оценке качества модели следует применятьRMSЕ, который дает более четкую картину реализации метода.

Следует также отметить, что для всех моделей в качестве дополнительных регрессоров использовались суммы гармоник, что повысило точность моделирования. Кроме того, наиболее «успешной» моделью является ARIMA, реализованная на базе алгоритма Хиндмана – Хандакара.

Количество чеков как характеристика покупательского потока: анализ и прогнозирование

Количество чеков является основой оценки работы любого розничного магазина. В частности, оно характеризует интенсивность покупательского потока, который обслуживает магазин. Также показатель участвует при расчете важных финансовых метрик – например, при расчете среднего чека. В любом случае, количество чеков является обобщенной оценкой исполнения тех задач, которые ставит перед собой предприятие – покупательский поток влияет и на прибыль, и на операционные расходы, и на управление товарными запасами. По нему также де- лают срез успешности проведенных маркетинговых мероприятий.

Важность количества чеков для оценки около розничного (ресторанный, гостиничный) и розничного бизнеса подтверждается исследованиями в этой области: анализ показателя как определяющего объем выручки для ресторанно-гостиничного бизнеса можно найти в работах [22; 23]. Количество чеков характеризует доступность торговой точки для покупателя, а исследование [24], в котором анализируются транзакционные данные с позиции получения информации о лояльности клиентов и покупателей, расширяет понимание того, что количество чеков – это фундаментальный параметр в розничной торговле.

Следовательно, к процедуре прогнозирования данного ключевого показателя необходимо отнестись с особым вниманием.

В частности, следует изучить сезонность рядов, внешнюю информацию, которая может способствовать улучшению качества прогноза, а также внимательно относиться к самим фактическим данным, очищая их от ошибок.

Для прогнозирования данного показателя будут применяться все рассматрива- емые в статье методы. Кроме того, будет использоваться широкий круг экзогенных пе- ременных:

• 1.    Данные о наличии государственного, негосударственного и религиозного праздника за период. Отметим, что для большинства методов (кроме модели Prophet, ввиду ограничений ее спецификации) используется порядковый номер дня праздника в качестве еще одного предиктора.

• 2.    Сезонность характеризуется как годовым периодом, так и недельным. Она задается с помощь фиктивных переменных, а также рядов Фурье.

• 3.    Учитывается также сезонность в рамках месяца, которая связана с сезонностью роста доходов населения (получение заработной платы). Подобная зависимость моделируется полиномом 5-й степени от номера дня в месяце, что также включается практически во все модели, кроме Prophet.

В качестве исходных данных для мо- делирования использовались ежедневные значения количества чеков в одном из магазинов розничной сети г. Ижевска. Ниже приведен график прогнозов на тестовой выборке по классическим методам (ARIMA, ETS) прогнозирования и фактические значения по количеству чеков (рис. 2).

5000 о inininininC0C£>C£>C£>C£>C£>C£>C£>C£>C£>C£>C£>C£>C£>C£>C£>C£)C£>C£> x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—   x—

OOOOOOOOOOOOOOOOOOOOOOOO CMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCMCM ^^^с^с^^^с^с^о6о6^^юююсЬсЬ|<1<ос>ос>оо ^^^^^PPPPPPPPPPPPPPPPPPP ^inojcONO^N^COOnN^LfiojNcod^S^^cd Ox-M^-(N^(MOMO(NOx-Ox-M^(Nx-(MOMOv-

Факт                     ARIMA                     ETS

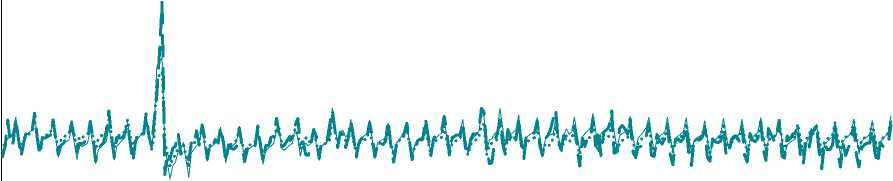
Рис. 2. Динамика количества чеков с прогнозами (классические методы прогнозирования)

На рис. 2 продемонстрирована хорошая аппроксимация фактических значений классическими методами. Далее приводится аналогичный график с прогнозами чеков с помощью более современных методов (Prophet, CES, BSTS) (рис. 3).

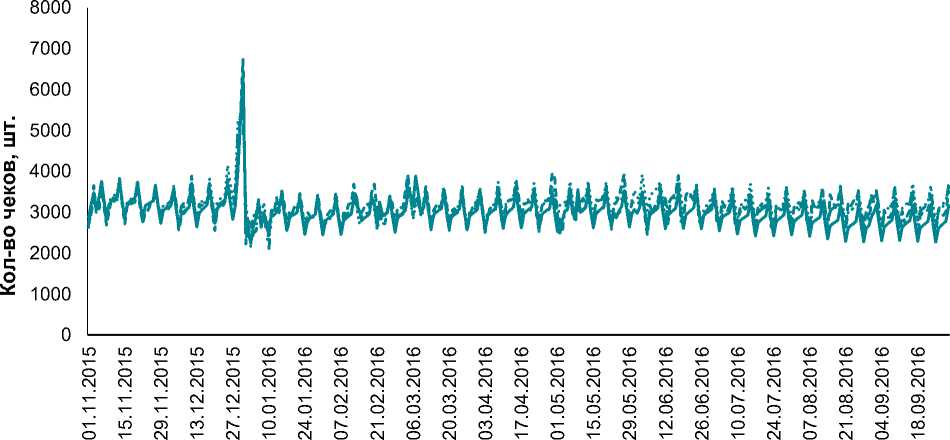
Факт                 Prophet                 CES                 BSTS

Рис. 3. Динамика количества чеков с прогнозами (современные методы прогнозирования)

Согласно рис. 3 обнаружена высокая степень подгонки моделей на тестовой выборке.

Далее на рис. 4 показан средний прогноз.

Средний прогноз формируется по всем методам, кроме модели экспоненциального сглаживания (ETS). Такой подход применяется из-за высокой коррелирован-ности прогнозов по методам ETS и CES.

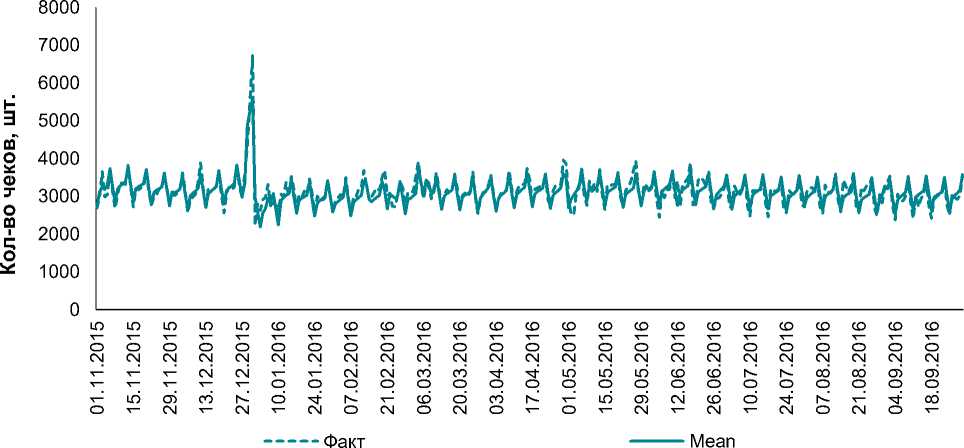
Рис. 4. Динамика количества чеков со средним прогнозом

По указанным метрикам лучшей из двух моделей является CES. В табл. 2 приведены метрики прогнозов.

Таблица 2

Результат тестирования методов прогнозирования для количества чеков

Метрика качества	Prophet	ARIMA	ETS	CES	BSTS	Mean
RMSE	240,46	224,40	228,54	227,54	230,86	188,69
MAE, %	6,05	5,26	5,30	5,40	5,47	4,43

Из табл. 2 видно, что значение среднего арифметического по прогнозам имеет лучшие метрики в сравнении с остальными прогнозами.

Следует отметить, что как для температурного режима, так и для количества чеков наиболее точным методом является ARIMA. В отличие от авторегрессионного метода достоинством иных методов, как бы- ло отмечено в предыдущем разделе, является возможность разложить ряд на четкие компоненты – тренд, сезонность, ошибка – что, безусловно, повышает интерпретируемость методов, позволяет сделать выводы о характере исследуемой целевой переменной. Тем не менее основной задачей исследования является повышение точности моделей, кото- рые оцениваются с помощью заданных метрик. Более того, проведенное исследование показало, что на значения метрик разного типа влияют особенности в прогнозируемой целевой переменной, что свидетельствует о правильности применения комплекса метрик для получения корректных результатов. Заключение

Исследование показало, что прогнозирование ключевых факторов, влияющих на дея- тельность торгового предприятия, является важным этапом подготовки качественных управленческих решений. Само прогнозирование данных обобщенных показателей может быть использовано при реализации более сложного моделирования, например в рамках прогнозирования по конкретной номенклатурной позиции.

Использованные методы прогнозирования временных рядов позволяют делать довольно точный прогноз с малым уровнем ошибки на достаточно длительных проме- жутках времени (в рассматриваемом исследовании этот период составил примерно год). Следовательно, на более коротких промежутках времени предложенный инструментарий прогнозирования будет давать еще более точные результаты. Это важно с точки зрения дальнейшего развития методов оперативного планирования и управления запасами предприятия.

Тем не менее прогноз погодных условий не может быть реализован только на основании временного ряда температур и понимании сезонности процесса. Для управленческих целей и в случае отсутствия возможности доступа к более совершенным внешним прогнозам (Яндекс. Погода, rp5, Gismeteo и др.) подобный прогноз может быть использован для принятия обоснованных управленческих решений. В связи с тем что какая-либо средняя оценка из всех рассматриваемых прогнозов не является эффективной ввиду наличия серьезных шумов для применяемых методов прогнозирования, в работе предложено использовать метод ARIMA-моделирования.

В исследовании также показано, что решающее значение для прогнозирования деятельности розничной сети имеет показатель количества чеков. В связи с этим при моделировании должна учитываться информация по экзогенным переменным – праздникам, их длительности, сезонности в доходах населения. По итогам моделирования лучшим прогнозом является среднее по несильно коррелированным методам, что говорит о возможности создания успешной комбинации на основе рассмотренных моделей, в том числе и нелинейной. Подобного рода комбинацию, взвешенную по ошибкам, можно увидеть в работе [25].

Дальнейшим этапом исследования может являться использование предложенного инструментария в создании системы прогнозирования товарного спроса на розничном предприятии. Кроме того, перспективным направлением может считаться разработка системы планирования в организации розничной и околорозничной торговли на базе методов прогнозирования с помощью инструментов анализа временных рядов.