Прогнозирование метрологических характеристик в титриметрии с использованием метода Монте-Карло

Разработка методик количественного потенциометрического и визуального индикаторного титрования путем экспериментального поиска оптимальных с точки зрения метрологических характеристик анализа условий - процесс трудоемкий и длительный. Поэтому разработка теоретических способов прогнозирования погрешностей результатов анализа представляет существенный теоретический и практический интерес.

Известны разнообразные подходы к прогнозированию систематических погрешностей титриметрии, основанные на математическом моделировании кривых титрования [1, 2]. В частности, авторами [2] предложено использовать степень протекания реакции в точке эквивалентности в качестве критерия возможности количественного определения. Вместе с тем, широко известно, что в точке эквивалентности существенно возрастают случайные погрешности измерения pH, обусловленные резким снижением буферной емкости титруемого раствора. Причем, чем больше степень протекания реакции, тем выше эта погрешность. Поэтому при прогнозировании возможности количественных определений следует также принимать во внимание случайные составляющие погрешностей. Прогнозирование случайных погрешностей является более сложной задачей, связанной с построением и исследованием в вычислительном эксперименте стохастических моделей кривых титрования. Поэтому работы по прогнозированию случайных погрешностей немногочисленны [3, 4]. В работах [3, 4], при стохастическом моделировании по методу Монте-Карло, принимают во внимание только инструментальную погрешность измерения аналитического сигнала на заключительной стадии анализа. Вкладами в отклик погрешностей измерения прочих величин, таких как объем аликвотирования пробы, объёмы добавляемого титранта и др. пренебрегают. Кроме того, моделирование осуществляют с использованием специальных вычислительных программ, малодоступных широкому кругу аналитиков.

Целью данной работы является изучение возможности применения метода Монте-Карло (метода статистических испытаний) [5] в вычислительной среде MS Excel для построения стохастических моделей кривых титрования и прогнозирования случайных погрешностей результата анализа на их основе. Здесь мы ограничимся моделированием титрования сильной кислоты щелочью и только некоторыми примерами отыскания конечной точки титрования (КТТ). Основное внимание в работе уделим методологии стохастического моделирования кривых титрования, а также технологии алгоритмизации моделей средствами электронных таблиц Excel.

Построение стохастической модели

Исходя из общей теории моделирования равновесий в титриметрии [6], построение модели начнем с записи уравнения кривой титрования в неявной форме:

Аналитическая химия

T(va^0H,pH) = (v4v0j4io-pH-io^^ (1) где V0 - начальный объем кислоты в сосуде для титрования; Уон - переменный объем добавленной щелочи; ¥а - аликвота стандартного раствора кислоты; Сн и сОн - концентрации (моль/л) тит-ранда и титранта, соответственно. Переменные ¥а, ¥он и pH будем считать независимыми случайными величинами, возможные значения которых (х^) распределены по нормальному закону. Согласно принципу Монте-Карло, возможные значения будем разыгрывать по методу обратной функции [5]:

Xj = М(х) + F"1 (^) • ох, (2) где М(х) - математической ожидание (действительное значение) переменной; F(x) - функция Лапласа-Гаусса; ii - возможные значения равномерно распределенной на интервале (0,1) случайной величины R, т.е. случайные числа; ох - стандартное отклонение переменной. Обратим внимание на то, что, в отличие от [3, 4], мы одновременно разыгрываем несколько случайных величин, т.е. имеем дело с многофакторным методом Монте-Карло.

В результате вычислений по уравнениям (1) и (2) получают отдельную реализацию кривой титрования в виде табличной функции pH от математического ожидания М(¥он)- Аналитической серией (выборкой) является совокупность п реализаций. Объем выборки п = 20, как это принято при разработке методик анализа [7]. Количество и расположение m точек на кривой титрования в первую очередь определяется алгоритмом отыскания КТТ. Далее, следуя алгоритму метода обработки, из табличной функции находят объём щелочи в точке эквивалентности ¥е, который используют для расчета результата определения по закону эквивалентов. По выборке объёма п оценивают среднее и стандартное отклонение результата анализа.

Уравнения (1) и (2) в сочетании с принятым для того или иного метода алгоритмом установления КТТ назовем стохастической моделью метода (СММ). Стохастическую модель несложно реализовать в виде формы листа электронной таблицы Excel. Форму листа образует совокупность ячеек, связанных формулами. Форма листа является программой, поскольку позволяет производить повторные вычисления с новыми данными по прилагаемой к программе инструкции. Ниже приводится общая схема использования СММ:

Шаг 1. Решают уравнение (1) относительно pH с детерминированными значениями ¥а, ¥он? а также с известными сн? сОн и pKw. При этом ¥Он задают с постоянным или, в общем случае, переменным шагом. Другими словами, вычисляют не нагруженную погрешностями идеальную кривую титрования.

Шаг 2. Для каждой точки, вычисленной на шаге 1 кривой титрования, разыгрывают значения ¥'он-

ШагЗ.С использованием результатов, полученных на двух предыдущих шагах, решают уравнение (1) относительно pH, так же как на 1-м шаге, но уже со случайными значениями переменных. При этом pH приобретает свойства случайной величины, а его зависимость от неслучайных значений ¥Он можно считать случайной функцией.

Шаг 4. Если изучают инструментальное титрование, тогда для каждой точки титрования дополнительно разыгрывают возможные погрешности измерения pH, которые накладывают на значения pH, полученные на 4-м шаге, см. уравнение (2).

Шаг 5. Обрабатывают полученные на шаге 4 или 5 результаты вычислительного эксперимента по выбранному алгоритму отыскания КТТ.

Можно видеть, что описанная выше общая схема стохастического моделирования имитирует последовательность основных стадий, с которыми имеет дело аналитик, выполняя единичное титрование.

Для большей приближенности модели к эксперименту необходимо априори задать возможные значения стандартных погрешностей ¥а, ¥он и pH. В этой работе погрешности измерения объёмов оценивали с использованием справочника [8]. Будем полагать, что орН = 0,02, как в случае использования pH-метров обычной точности. Другие детали построения СММ будут обсуждены ниже при рассмотрении частных моделей.

О прогностических возможностях моделей судили при сопоставлении результатов вычислительных экспериментов с результатами лабораторных анализов.

Экспериментальная часть

Растворы NaOH, НС1 и KNO3 готовили из веществ реактивной чистоты на дистиллированной воде. Для титрования использовали 0,1 моль/л бескарбонатную щелочь, которую хранили в склянке микробюретки с автоматическим нулем, защищая её от углекислого газа ловушками с натронной известью. Стандартный 0,1 моль/л раствор соляной кислоты приготовляли из фикса-нала. Ионную силу титруемого раствора поддерживали на постоянном уровне 0,1 моль/л посредством индифферентного электролита.

Аликвотирование НС1 производили пипеткой Мора с номинальным объёмом 5 мл и предельным отклонением от номинальной вместимости ±0,02 мл. Начальный объем раствора в стакане для титрования задавали равным 50 мл. Титрант дозировали из бюретки с номинальной вместимостью 10 мл, минимальной дискретностью отсчета 0,02 мл и предельным отклонением от номинальной вместимости ±0,02 мл. В процессе титрования раствор достаточно интенсивно перемешивали якорьком магнитной мешалки.

В процессе титрования измеряли pH раствора с использованием электродной пары из стеклянного индикаторного и хлорсеребряного сравнительного электродов на pH-метре pH-121. Предельная погрешность измерения потенциала на pH-121, согласно его паспорту, составляет ±1 мВ. Специально была изучена воспроизводимость измерения pH стандартных буферных растворов с pH 4,01 и pH 6,86 в сериях из 20 измерений. При этом получена оценка стандартного отклонения Орн = 0,02, которая не зависела от pH. Шкалу прибора настраивали в концентрационной шкале по 0,01 моль/л раствору соляной кислоты, принимая pH этого раствора равным 2 ед. pH на фоне 0,1 моль/л KNO3.

Результаты и их обсуждение

Пример 1. Отыскание конечной точки титрования по первой производной

Обычно КТТ находят из графика зависимости |ApH/AV| от объёма титранта как точку максимума. Несмотря на кажущуюся простоту, метод непросто автоматизировать. Альтернативой графическому способу является табличный вариант метода, поскольку процедуры работы с многомерными массивами и матрицами легко формализовать и, как следствие, автоматизировать.

Нами предложен метод, названный методом максимальной крутизны (ММК), в котором поиск Уе осуществляется только на интервале АУе, охватывающем слева и справа максимум дифференциальной кривой. Этот интервал локализации Ve находим как результат предварительного титрования анализируемого раствора с достаточно большим шагом добавления титранта h. Последующее «точное» титрование проводят с шагом h = 0,02 мл, равным минимальной цене деления шкалы микробюретки (или титрант добавляют по каплям объема 0,02 мл, как при классическом титровании по макрометоду). В численных методах решения уравнений этот прием называют сканированием с переменным шагом.

Стохастическая модель метода максимальной крутизны показана на рис. 1 на примере установления концентрации щелочи по 0,1 моль/л стандартному раствору соляной кислоты. Считаем, что раствор щелочи также предварительно стандартизован другим методом. Исследовательской задачей является установление метрологических характеристик ММК: оценка правильности и воспроизводимости метода. Дополнительной задачей является выяснение причин плохой воспроизводимости значений pH на скачках титрования.

Вначале рассчитывают идеальную кривую титрования по уравнению (1) с параметрами, которые приведены в блоке ячеек A4:F5. При заданном объёме добавленной щелочи (см. массив с именем «V, мл») решают уравнение кривой титрования относительно pH численно посредством утилиты «Подбор параметра». В расчетах использовали концентрационную константу автопротолиза воды, вычисленную по уравнению Девиса. Далее разыгрывают возможное значение взятой на титрование аликвоты соляной кислоты. Эта процедура записана формулой в ячейке С8. По уравнению (2) находят случайное значение VV Затем нагружают погрешностями Уон, разыгрывая возможные значения объёмов добавленной щелочи в каждой точке кривой титрования. Для этого формулу, занесенную в ячейку D22, копируют в столбец D12:D21. При этом получают вектор Уон- Теперь можно приступить к вычислению новых значений pH' с использованием уравнения кривой титрования (1), как это было сделано прежде при вычислении идеальной кривой, с той лишь разницей, что при расчетах используют возможные значения У’а и Уон- В нотации

Аналитическая химия

Excel уравнение (2) имеет вид =($D$4+D12)*(10^A-E12-10^A(E12-$A$5))-$C$5*$B$8+D12*$B$5, для первой ячейки в столбце Т(). Аналогичные формулы записаны в остальных ячейках диапазона Т(). Вектор pH' восстанавливают, применяя утилиту «Подбор параметра». На заключительном этапе вычислений нагружают погрешностями измерения pH вектор pH' и получают столбец pH”. Для этого в колонке pH” записана формула массива ={Е12:Е21+$Н$5*НОРМСТОБР(СЛЧИС())}. Таким образом получают одну из возможных реализаций кривой титрования в координатах (V_Oh_? pH”). Теперь эту кривую можно обрабатывать по тому или иному алгоритму отыскания V_e.

	А	В	1 с	; d	1 Е	1 F	1 G	1 Н	I
1	Моделирование погрешностей титрования методом					Монте-Карло
2
3	Парамет,	ры стохастической модели
4	pKw	Сон, М	сн, М	V0, мл	Va, мл	h, мл	Оу а	ОрН	Оу (ОН)
5	13,78	0,100	0,100	50,00	5,00	0,02	0,01	0,02	0,01
6
7	Разыгрывание аликвоты
8	N\, мл=	4,99	=$E$5+$G$5 *НОРМСТОБР(СЛЧИС())
9
10		Идеальная	кривая	Стохастическая модель
II	№ п/п	Vqh? мл	pH	Vqh, мл	pH’	ТО	pH"	АрН"
12	1	4,90	3,74	4,90	3,81	2ДЕ-07	3,82	0,12
13	2	4,92	3,84	4,92	3,91	3,ЗЕ-08	3,93	0,05
14	3	4,94	3,96	4,93	3,99	9,6Е-07	3,98	0,06
15	4	4,96	4,14	4,94	4,05	-ЗЕ-07	4,04	1,36
16	5	4,98	4,44	4,99	5,40	6,4Е-08	5,40	2,44
17 ;	6	5,00	6,89	4,99	7,81	8,ЗЕ-08	7,84	1,59
18	7	5,02	9,34	5,01	9,43	7,2Е-07	9,43	0,31
19	8	5,04	9,64	- 5,04	9,75	-2Е-07	9,74	0,15
20	9	5,06	9,82	5,06	9,89	9Е-08	9,90	0,13
21	10	5,08	9,94	5,09	10,04	2,8Е-07	10,03
22			=В22+$1$5 *НОРМСТОБР(СЛЧИС())
23	Результат определения
2 4	Ve, МЛ=	=ИНДЕКС(В 12:В21 ;ПОИСКПОЗ(МАКС(Н 12 :Н20);Н 12 :Н20;0))+$Е$5/2

Рис. 1. Форма листа Excel для исследования метрологических характеристик ММК

Для обработки кривой по ММК нам необходим вектор первых разностей АрН" (см. рис. 1). Искомое значение щелочи в точке эквивалентности возвращает формула в ячейке В24, которая отыскивает максимальное значение в массиве АрН", затем находит соответствующий максимуму объём в векторе Vqh- Для окончательной оценки V_e, найденное значение исправляем на величину ^h в соответствии с теоремой Лагранжа о среднем дифференциального исчисления.

Для моделирования параллельных определений достаточно повторить в электронной таблице весь цикл вычислений с вновь разыгранными значениями случайных величин. По результатам 20 реализаций нашли сОн = 0,1000 моль/л с относительным стандартным отклонением sr = 0,2 %. Таким образом, можно предвидеть, что если при установлении концентрации щелочи использовать пипетку 2-го класса точности, pH-метр обычной точности, а титрование проводить по полумикрометоду, то полученная методом максимальной крутизны оценка концентрации будет несмещенной и точность оценки будет удовлетворительной для решения большинства аналитических задач.

Для сопоставления прогноза с экспериментально наблюдаемыми метрологическими характеристиками ММК выполнили 4 параллельных титрования. Найдено сон = 0,1180 моль/л с относительным стандартным отклонением sr = 0,3 %. Экспериментальная оценка погрешности метода незначимо отличается от прогнозируемого значения, поскольку по критерию Фишера Fexp = 2,5 < Ftab(0,05; 3; 19) = 3,1. Однако в данном случае применение F-статистики не вполне оправдано, поскольку в вычислительном эксперименте было установлено дискретное распределе ние Сон? которое можно свести к распределению Бернулли. Очевидно, что дискретность отдель ных результатов титрования обусловлена тем, что по алгоритму метода максимальной крутизны титрант дозируют равными дискретными порциями. В ходе лабораторного эксперимента при 4-кратном воспроизведении процедуры титрования была найдена зависимость стандартного отклонения воспроизводимости sph от pH вдоль кривой титрования. Эта зависимость показана кривой 2 (рис. 2). Аналогичная колоколообразная зависимость установлена в имитационном эксперименте, см. кривую 1 на рис. 2. Можно видеть, что стохастическое моделирование позволяет довольно точно прогнозировать как форму кривой погрешностей, так и меру рассеяния pH. Согласно прогнозу, для нашего примера возможны стандартные отклонения на уровне 2 ед. pH. Найденное в лабораторном эксперименте максимальное стандартное отклонение размером в 1,3 ед. pH находится несколько правее pH 7, при котором буферная ёмкость титруемого раствора минимальна. Очевидно, что рассеяние pH вдоль кривых титрования нельзя объяснить

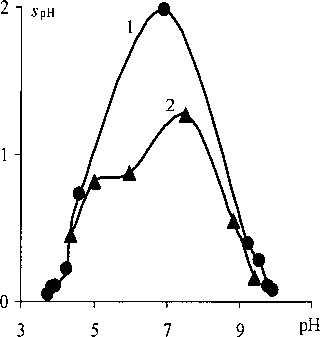
Рис. 2. Воспроизводимость pH вдоль кривых титрования при вычислительном (1) и лабораторном (2) эксперименте

только инструментальной погрешностью измерения pH, поскольку инструментальная погрешность При = 0,02 ед. pH, как это было задано при моделировании с учетом результатов измерения pH буферных растворов. Обращает на себя внимание близкое расположение нижних ветвей кривых 1 и 2. Это указывает на достаточно высокую прогностическую способность предложенного нами подхода к стохастическому моделированию кривых титровании на основе метода Монте-Карло.

Анализ результатов стохастического моделирования позволяет проранжировать вклады случайных величин ¥а, VOH и pH в общую погрешность метода МК: ¥а > ¥Он >рН. Отсюда следует возможность оптимизации определений за счет, прежде всего, повышения точности аликвотирова-ния стандартного раствора кислоты. Вместе с тем эта последовательность обращается, если измерения кривой проводят на участках с большой буферностью, т.е. вдали от точки эквивалентности.

Пример 2. Метод скачка титрования

Этот метод называют индикаторным методом, если КТТ устанавливают по изменению окраски кислотно-основного индикатора, а также методом фиксированного потенциала (pH) при индикации кривой потенциометрическим методом. И в том, и в другом случае точность измерения pH не существенна. Важно зарегистрировать область перехода pH раствора от состояния недо-титрованности к состоянию оттитрованности. В математической записи это условие имеет вид:

Ve = V(pH > pHInd). (3)

Стохастическую модель метода скачка титрования (МСТ) строили в электронных таблицах так же, как в первом примере. Для создания вычислительной программы можно просто отредактировать форму на рис. 1 в части алгоритма отыскания КТТ. В отличие от первого примера, погрешности измерения pH во внимание не принимаем. Поиск КТТ на скачке титрования производится с помощью библиотечных функций Excel из категории «Ссылки и массивы», также как в первом примере, но уже не по дифференциальной, а по интегральной кривой титрования. Условие (3), записанное в нотации Excel, имеет вид: ИНДЕКС(¥;ПОИСКПОЗ(р1;рН;-1)).

Методом Монте-Карло исследованы метрологические характеристики МСТ при аттестации раствора щелочи при тех же условиях, что и в примере 1. Основные результаты моделирования приведены в табл. 1. Видим, что наш метод прогнозирует достаточно высокое качество анализа по МСТ.

Аналитическая химия

Таблица 1

Прогнозируемые метрологические характеристики МСТ при титровании 0,01 М HCI по полумикрометоду 0,1 М раствором щелочи

	pH перехода
	5	6	7	8
Сон? М	0,0998	0,0998	0,0998	0,0998
s, М	0,0003	0,0003	0,0003	0,0003
Sr, %	0,27	0,30	0,30	0,30
texp	0,65	0,66	0,66	0,66
W0,05; 19)	2,4	2,4	2,4	2,4

Можно сделать вывод о том, что при стандартизации щелочи по сильной кислоте для установления КТТ можно выбирать любые индикаторы с индексами перехода от 5 до 8 (любые фиксированные значения pH в этом интервале). При этом систематическая ошибка отсутствует. Использование любого из этих индикаторов приводит к равной точности определения. Метод скачка титрования несколько проигрывает в точности методу максимальной крутизны, что следует из сравнения стандартных отклонений этих методов по F-критерию: Fexp = (3 ■ 10-4)2/(2 • 10"4)2> > Ftab(0,05;19;19) = 2,17.

В табл. 2 приведены результаты установления концентрации того же, что и в примере 1 раствора щелочи при pH-метрическом титровании до нескольких наперед заданных значений pH. Предсказанные в вычислительном эксперименте метрологические характеристики МСТ хорошо согласуются с характеристиками, найденными экспериментально. Во-первых, лабораторный эксперимент подтвердил прогноз о несколько большей точности ММК по сравнению с МСТ. Во-вторых, экспериментальные оценки стандартных погрешностей МСК во всех случаях, кроме случая титрования до рН = 5, даже совпали с теоретическими оценками в табл. 1. Кроме того, результаты аналитического определения концентрации щелочи по МСТ не отличаются по критерию Стьюдента ttab(0,05;7) = 2,8 от результата сон= 0,1180 моль/л, найденного по ММК. Этот факт косвенно подтверждает теоретический вывод об отсутствии систематической погрешности при титровании сильной кислоты щелочью по методу скачка титрования.

Таблица 2

Результаты стандартизации щелочи методом титрования до фиксированного pH

	Фиксированные значения pH
	5	6	7	8
Сон? M	0,1186	0,1182	0,1176	0,1176
s, М	0,0005	0,0003	0,0003	0,0003
Sr, %	0,45	0,27	0,27	0,27
texp	2,2	1,2	1,2	1,2

Полученные в данной работе результаты указывают на перспективность использования электронных таблиц Excel для стохастического моделирования и прогнозирования погрешностей титриметрии. Табличный процессор позволяет имитировать достаточно сложные, многостадийные и многофакторные измерительные процедуры. Широкая доступность и распространенность этого программного продукта позволяет рекомендовать его для применения не только при обучении [9], но и в практической работе по улучшению метрологических характеристик аналитических методик.

Выводы

• 1.    С использованием многофакторного метода Монте-Карло предложен новый подход к прогнозированию метрологических характеристик в титриметрии.

• 2.    На примерах стохастических моделей стандартизации щелочи по сильной кислоте методом максимальной крутизны, а также методом скачка титрования показана высокая прогностическая способность моделей.

• 3.    Предложены Excel-программы для реализации метода.