Прогнозирование налога на доходы физических лиц с использованием искусственных нейронных сетей

Хандаров Федор Владимирович; Дондоков Зорикто Бато-Дугарович; Handarov Fedor Vladimirovich; Dondokov Zorikto Bato-Dugarovich

Научные статьи \ Общие вопросы науки и культуры \ Информационные технологии. Вычислительная техника. Обработка данных

Прогнозирование налога на доходы физических лиц с использованием искусственных нейронных сетей

Автор: Хандаров Федор Владимирович, Дондоков Зорикто Бато-Дугарович

Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths

Рубрика: Системный анализ и информационные технологии

Статья в выпуске: 1, 2012 года.

Бесплатный доступ

В статье излагается методика прогнозирования налога на доходы физических лиц с использованием аппарата искусственных нейронных сетей. Приводятся полученные результаты.

Временные ряды, налоговое прогнозирование, отбор признаков

Короткий адрес: https://sciup.org/14835059

IDR: 14835059 | УДК: 004+336.221

Personal income tax forecasting using artificial neural networks

The paper deals with methods of personal income tax forecasting using artificial neural networks. The results are described.

Текст научной статьи Прогнозирование налога на доходы физических лиц с использованием искусственных нейронных сетей

Одной из важных проблем в региональном экономическом планировании является прогнозирование налоговых поступлений; в частности, основного вида прямых налогов – налога на доходы физических лиц. Данный вид налога является третьим по величине отчислений в бюджет и отличается следующими важными особенностями:

• объектом обложения данным налогом служит именно доход, реально полученный налогоплательщиком;
• его плательщиками является практически все трудоспособное население страны;
• при прочих равных условиях он легче других налогов контролируется налоговыми органами, от его уплаты сложнее уклониться недобросовестным налогоплательщикам.

При этом специфика и сложность прогнозирования НДФЛ обусловлена влиянием множества трудно формализуемых факторов, неполнотой и противоречивостью исторических данных. Трактовка полученных результатов также затруднена в силу чисто экономических причин, вроде: сокрытия доходов, неуплаты налогов, теневого оборота и т.п.

В работе описывается методика прогнозирования рассматриваемого вида налога на основе применения аппарата искусственных нейронных сетей, производится её сравнение с другими методами прогнозирования, приводится интерпретация полученных результатов: оценка качества полученных прогнозов.

Вычислительные эксперименты в работе производятся по данным налоговых поступлений по Республике Бурятия. Временной интервал исторических данных, используемых для построения системы прогнозирования, составляет 3 года с разбивкой по месяцам.

Описание методики

В ходе эксперимента рассматривались 10 экономических показателей, по одному из которых («Поступление НДФЛ в бюджет города Улан-Удэ») требовалось построить прогноз (табл. 1), остальные 9 показателей предположительно считаются влияющими. Кроме того, требовалось определить степень подобного влияния и построить модель прогнозирования «Поступлений НДФЛ».

Таблица 1

Экономические показатели

№	Показатель
1	Индексы промышленного производства
2	Добыча полезных ископаемых
3	Обрабатывающие производства
4	Производство и распределение электроэнергии, газа и воды
5	Продукция сельского хозяйства в хозяйствах всех категорий
6	Грузооборот всех видов транспорта на основе коммерческого грузооборота
7	Объем работ по виду деятельности «строительство» (в фактических ценах соответствующих лет)
8	Численность занятого в экономике населения
9	Среднемесячная номинальная начисленная заработная плата одного работника
10	Поступление НДФЛ в бюджет города Улан-Удэ

Методика заключалась в переборе k-сочетаний показателей, для получаемого всякий раз k-мерного временного ряда строилась модель прогнозирования. В качестве аппарата прогнозирования использовались искусственные нейронные сети с применением метода «взвешенного скользящего окна» [1]. Стоит отметить, что в качестве непосредственного механизма прогнозирования, вообще говоря, возможно использование любого другого подходящего аппарата, однако такие преимущества искусственных нейронных сетей, как возможность обучения, решение задач при неизвестных закономерностях, устойчивость к шумам, адаптация к окружающим условиям и др., вполне определяют выбор авторов.

В качестве механизма настройки весов и подбора структуры нейронных сетей использовался эволюционный алгоритм. Особью для эволюционного алгоритма является искусственная нейронная сеть, в качестве хромосомы рассматривается вектор вещественных чисел – множество весов связей ИНС, содержащий также информацию о входном и выходном нейронах для каждой связи.

При скрещивании два графа ИНС сортировались топологически обходом в ширину, начиная с входных нейронов, с сохранением фиксированного количества и нумерации входных и выходных нейронов. Таким образом, для любых двух ИНС возможно было установить «одинаковые» и «различающиеся» элементы вектора представления – хромосомы. Так, например, рассмотрим две ИНС с одинаковым количеством и нумерацией входных и выходных нейронов (рис. 1).

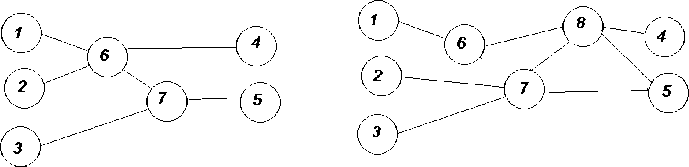
Рис. 1. Пример двух различных ИНС

Полученные в результате поиска в ширину векторы связей будут иметь следующие «совпадающие» связи ИНС (выделены подчеркиванием).

1	2	3	6	6	7
6	6	7	4	7	5

1	2	3	6	7	7	8	8
6	7	7	8	8	5	4	5

Рис. 2. «Совпадающие» связи ИНС

Для особей были определены операции инициализации, оценивания, отбора для скрещивания, скрещивания, мутации, редукции и селекции.

Критерием остановки процесса настройки нейронной сети является достижение максимального количества итераций или сходимость популяции к заданной величине ε. Таким образом, в описываемой методике критерием оценки качества отбора показателей и одновременно критерием качества полученной сетевой структуры и настройки весов сети является качество прогноза, совершаемого нейронной сетью.

Полученные результаты и сравнение со статистическими методами

В качестве альтернативных методов прогнозирования рассматривалось построение уравнения регрессии с предварительным проведением факторного анализа для отбора влияющих на величину НДФЛ показателей и без него.

В таблице представлены реальные величины НДФЛ в 2011 году («Ре-альн.»), а также результаты, полученные с использованием описанного подхода («ИНС-1» – «ИНС-5») и статистических методов («ФА+лин. регр.» и «Лин. регр.»). В последней строке приведено значение среднеквадратической ошибки для каждого метода.

сч

о сч^

о 40

О in

о °ч

О 40^

о оо^

СП

оо"

04"

in"

40"

СП

40"

'хГ

сч"

ГП

пГ

СП

—.

СП

хГ

СП

ОО

оо

СЧ

оо

СП

►А

ОО

сч

тГ

Нн

сч

СП

сч

СП

чГ

сч

^н

сч

Он

ОО

СП

—

£—.

—.

—

СП

сп

+ о

СП

ОО

сч

^г

оо

чГ

ОО

сч

ОО

оо

тт

сч

сп

в о

СП

[^^

СП

^-А

^А

оо

сп

СО

со

о^

со

—.

сч"

ш"

сч"

о"

оо"

^-"

сч"

СП

о"

СП

сч

оо

оо"

£—.

СП

—.

сч

СП

—

тГ

сч

СЧ

1П

, 4

^н

сч

СП

сч

[—.

сч

СЧ

сч

СП

сЗ

-о

<о

о^

со

сч

СП

40"

оо"

in"

4о"

04"

чГ

ОО

СП

---

Он

^г

сч

СП

ОО

оо

сч

ОО

^^А

—.

сч

ОО

со

чГ

сп

О К

ОО

сч

чГ

Он

<о

1П

сч^

чГ

40^

—.

с^

о^

О^

СП

оо"

о^

40^

04"

40"

си"

СП

оо

сп"

04"

£—.

—

—.

чГ

—

оо

сч

—

СП

чГ

СП

г-Н

и—1

г-Н

г-н

о^

ос.

40^

04^

40^

ОО

чо

Рн

04"

in"

СП

40"

—

ОО

сч

—

04"

—.

сч

ОО

£—.

СП

—

СП

—.

сч

ОО

СП

—

сч

г-~

сч

ОО

чГ

СП

чГ

^А

сч

оо

сч

[^^

□0

Щ Он

ОО

чГ

^А

ОО

чГ

—.

сч

чГ

К ^

ОО

сч

xj-

сч

[^^

Он

сч

^А

сч

чГ

СП

^А

сч

СП

[—.

1П

—.

СЧ

сп

оо

со

сч^

ОЧ

сч^

сч

сч"

о"

40"

оо"

сп"

04"

оо"

04"

4О"

. S3

г:

£—.

СП

1П

—

СП

§ ю

—

ОО

—.

чГ

[^^

СП

чГ

Он

сп

СП

Он 3

ОО

сч

° о

м о

Он

н ^

2 о

СЧ

г©Н

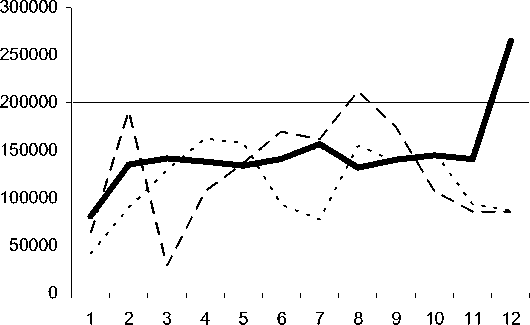
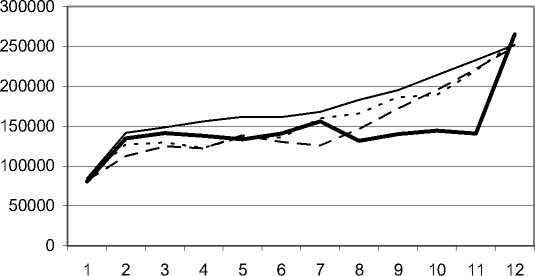
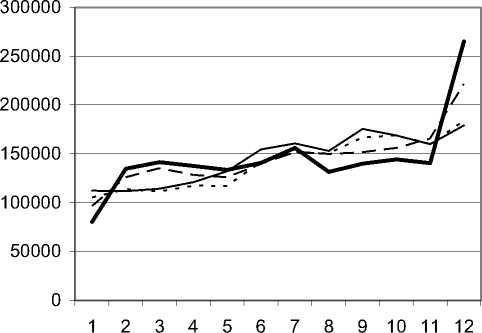
На рисунках 3а – 3в представлены графики, иллюстрирующие данные таблицы 2. Рис. 3а – лучшие (по ср.-кв. ошибке) прогнозы от нейронных сетей при k > 4 , т.е. ИНС, построенные на 5 и более сочетаниях показателей, – налицо неадекватность поведения и большая ср.-кв. ошибка. Рис.3б – лучшие результаты прогнозов ИНС, построенных на 4-х сочетаниях – при сокращении размерности k-мерного временного ряда лучше угадывается тренд, однако по величине ср.-кв. ошибки ИНС все еще уступают статистическим методам (для представленных ИНС использовались следующие наборы показателей: 7-8-9, 6-7-9, 7-8-9 по табл.1). Рис.3в – лучшая ИНС, построенная на 3-х сочетаниях (7-9 по табл.1), а также регрессионные модели с предварительным снижением размерности и без него.

Реальн.

ИНС-1

ИНС-2

Рис. 3а. Результаты прогнозирования

Реальн.

ИНС-3

ИНС-4

ИНС-5

Рис. 3б. Результаты прогнозирования

Реальн.

ФА+лин.регр. лин.регр.

ИНС-5

Рис. 3в. Результаты прогнозирования

По результатам проведенных экспериментов можно сделать выводы о том, что применение искусственных нейронных сетей для прогнозирования НДФЛ позволяет добиваться прогноза как минимум не хуже результатов, получаемых статистическими методами, а также о том, что предварительное снижение размерности позволяет повысить качество прогноза.

Заключение

Таким образом, применение рассмотренной методики позволяет получать адекватный прогноз, который может быть использован в качестве одного из контрольных инструментов при построении прогноза, поскольку в качестве оснований для прогнозирования используются лишь исторические данные, что, впрочем, при сохранении трендов вполне уместно. Предсказание же изменения трендов остается привилегией макроэкономических методов.

Налицо такие преимущества методики, как способность к выявлению скрытых связей, универсальность подхода, широкие возможности повторного использования (reusability), естественные возможности распараллеливания.

Список литературы Прогнозирование налога на доходы физических лиц с использованием искусственных нейронных сетей

Morantz B.H., Whalen T., Zhang P.G. A Weighted Window Approach to Neural Network Time Series Forecasting//Chapter 13 in P. Zhang (ed.) Neural Networks in Business Forecasting, IRM Press, 2004. -Р.251-265.
Eshelman L.J., Schaffer J.D. Real-coded genetic algorithms and interval schemata//Foundation of Genetic Algorithms 2. -1993. -P. 187-202.
Deb K., Kumar A. Realcoded genetic algorithms with simulated binary crossover: Studies on multimodal and multiobjective problems//Complex Systems. 9(6). -1995. -P. 431-451.
Herrera F., Lozano M. Adaptation of genetic algorithm parameters based on fuzzy logic controllers//Genetic Algorithms and Soft Computing. -1996. -P. 95-125.