Прогнозирование повреждений в мягких тканях стопы человека при действии экстремальных нагрузок

Глобальной целью исследований является рассмотрение процесса накопления повреждений в мягких тканях стопы спортсмена (мышцах, связках и сухожилиях) при приземлении на жесткую поверхность. Важную роль при изучении этих процессов играют напряжения, которые имеют место во всех структурах стопы. Знание напряжений имеет фундаментальное значение при понимании физиологии и патофизиологии стопы, и может представить очень ценную информацию для предотвращения и лечения повреждений. Нагрузка, действующая на структуры локомоторной системы человека при спортивных упражнениях, является одним из возможных стимулов сохранения или увеличения сопротивления биологических тканей повреждаемости. Однако, чрезмерная нагрузка может быть причиной микро- или макротравм анатомических структур.

Одно из первых рассмотрений вопроса о перенапряжении тканей у спортсменов состоялось на XII Международном конгрессе по спортивной медицине в 1958 г. в Москве. Большой доклад по этой проблеме сделал известный итальянский ученый Д. Ла Кава (D. La Cava) [1]. В нем он показал, что перенапряжение как процесс является патологическим фактором и его нельзя смешивать с физиологическим изнашиванием тканей, вызванным самой жизнью. Ла Кава высказал мысль о том, что в развитии микротравматического патологического процесса большую роль играют состояния, при которых оказывается нарушенным обмен веществ как местных тканей, так и всего организма. Наличие в организме очагов воспалительных процессов является предрасполагающим условием для перенапряжения тканей.

В некоторых исследованиях считается, что нагрузка является чрезмерной во многих спортивных упражнениях. Известно, что в течение одного года получают травмы от 25% до 50% бегунов [2], от 21% до 52 % теннисистов получают травмы опорно-двигательного аппарата в течение сезона [3]. Травмам подвергаются и спортсмены профессионалы и спортсмены любители. Так, например, известно, что среди людей, занимающихся спортивной аэробикой и получивших травму, 76% -инструкторы и 43% - их подопечные [4]. Эти цифры говорят о том, что проблема существует и необходимо предпринимать определенные шаги к исправлению ситуации.

При анализе спортивных повреждений должны быть рассмотрены самые различные вопросы, такие как: непосредственное исследование поврежденной анатомической структуры, тип повреждений, внешние силы, действующие на атлета при упражнениях, которые могут привести к травмам, действительные внутренние силы или напряжения, действующие в анатомической структуре до и во время повреждения, материальные свойства поврежденных структур и их критические пределы и другие. Однако одной из главных целей исследований, относящихся к спортивным повреждениям, должно быть уменьшение частоты этих повреждений.

По данным отделения спортивной травмы Центрального института травматологии и ортопедии [5, 6] частота повреждений мягких тканей по локализации распределяется следующим образом: нижние конечности - 62%; верхние конечности -22%; прочие - 16%. При этом наблюдается выраженная преимущественная зависимость между определенной группой биологических тканей и занятием определенным видом спорта.

В результате чрезмерных и однообразных нагрузок перенапряжение испытывает место перехода мышц в сухожилие и область прикрепления сухожилий к костной ткани [7]. Это нередко вызывает боли у спортсменов и невозможность продолжать тренировки.

На наш взгляд, анализ процесса накопления повреждений в мягких тканях стопы должен состоять из нескольких этапов. В качестве примера такого рода анализа спортивных движений предполагается рассмотреть приземление гимнаста на жесткую поверхность и возникающие при этом повреждения в мягких тканях стопы (связках, сухожилиях, мышцах).

Этапы анализа

• 1.    Определение начальных условий для последующего анализа, то есть применительно к нашей задаче необходимо определить кинематические характеристики движения человека до контакта с поверхностью приземления.

• 2.    Построение биомеханической модели движения человека и определение по заданному движению реакций, действующих на стопу.

• 3.    Построение структурной биомеханической модели стопы, которая отражала бы все биомеханические свойства объекта исследования (взаимодействие структурных элементов, их подвижность и так далее) и определение относительных перемещений структурных элементов и напряжений в мягких тканях стопы.

• 4.    Определение по известным напряжениям, возникающим в связках и сухожилиях стопы, возможного уровня накопления повреждений, учитывая их залечивание.

• 5.    Идентификация факторов, влияющих на возникновение повреждений в подвергнутых опасности структурах, и разработка стратегии обеспечения уменьшения возможных повреждений.

Модель приземления

Существует несколько подходов к построению биомеханических моделей, описывающих движение человека. Использование того или иного подхода зависит от предпочтений исследователя и тех целей, которые он перед собой ставит. Тем не менее, основной принцип построения остается неизменным – моделирование частей тела человека в виде твердых тел, соединенных между собой шарнирами и описание движения полученной системы при помощи уравнений Лагранжа II рода. Отличия могут заключаться в моделировании действия мышц и усложненном представлении некоторых элементов модели. Так, например, в работах [8, 9] действие мышц заменяется эффективными моментами в суставах, а в работе [10] вводится в рассмотрение модель мышцы с эффективным плечом мышцы, а также дополнительный элемент, описывающий рессорные свойства стопы.

Мы будем придерживаться подхода использованного в работах [8, 9]. Рассмотрим приземление гимнаста при вертикальном полете с высоты h , когда вектор скорости его центра масс перпендикулярен горизонтальной поверхности приземления, механические свойства которой известны. Тело спортсмена моделируется шестизвенной шарнирно соединенной стержневой системой: ступни, голени, бедра, торс и голова, плечи, предплечья. Геометрические и инерционные характеристики всех звеньев известны, а правые и левые части тела действуют синхронно, образуя единый элемент.

Характер полета и относительно небольшая скорость приземления позволяют пренебречь сопротивлением воздуха. Общие теоремы динамики, эквивалентные для случая вертикального полета вытянувшегося гимнаста задаче динамики точки, определяют скорость центра масс (ступней) в момент касания поверхности по известной формуле:

V 1 = 2ghk. (1) которая является начальным условием для дальнейших исследований.

Движение гимнаста с момента касания матов описывается системой дифференциальных уравнений второго порядка, число которых определяется числом степеней свободы стержневой модели. Сегменты тела предполагаются недеформируемыми, суставы заменяются шарнирами без трения (идеальными). Положение спортсмена определяется восемью обобщенными координатами: x_T, y T , ф 1 , ф ₂, ф 3 , ф 4 , ф ₅ , ф 6 , которые представлены на рисунке 1 ( x_T, y_T - координаты тазобедренного сустава).

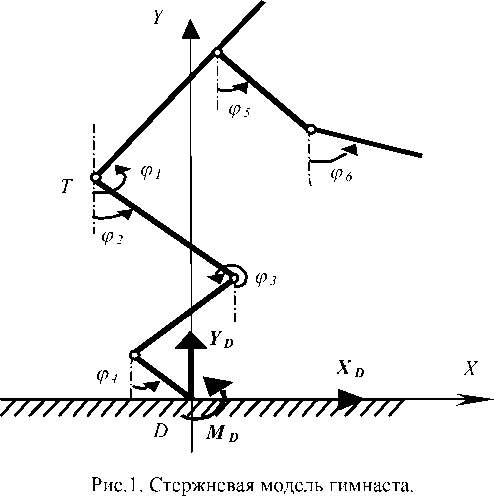
В нашей работе система уравнений получена с помощью уравнений Лагранжа II рода может быть записана в виде:

J_k ( q j ,q j ,q j , X d , Y d , M d , M J = 0, j,k = Ts, i = 1Д                 (2)

где q j - обобщенные координаты, X_D,Y_D - горизонтальное и вертикальное усилия, действующие на стопу (реакция поверхности приземления), M _D - приведенный к точке касания момент реакции опоры, M i - приведенные к суставам моменты мышечных усилий, 8 - число степеней свободы механической системы.

Конкретный вид уравнений (2) зависит от упрощений в шестизвенной стержневой модели спортсмена в связи с теми или иными задачами исследования движения гимнаста. Если известны все силовые воздействия (в том числе приведенные к суставам моменты мышечных усилий), то к системе уравнений (2) добавляются соответствующие начальные условия, и она решается аналитически для простых случаев или интегрируется численно. Обратная задача заключается в нахождении силовых воздействий по известной кинематике процесса приземления, которая определяется из эксперимента.

Модель стопы

Построению биомеханической модели стопы и исследованию ее механических свойств посвящены работы [11, 12]. Использование результатов этих исследований применительно к решаемой нами задаче напрямую невозможно, так как нас интересует поведение стопы в процессе движения человека, что не учитывается в предлагаемой [11, 12] модели. Тем не менее, некоторые идеи из этих работ будут использованы при построении модели стопы в нашей работе.

Стопа имеет аркообразную форму, воспринимающую нагрузку, приложенную к таранной кости со стороны большеберцовой и малоберцовой костей. Такая аркообразная форма сохраняется при действии нагрузки, что достигается за счет plantar aponeurosis - мышцы, которая простирается от выступа пяточной кости до плюснефаланговых суставов [13]. Основные опорные области стопы сконцентрированы под окончаниями (головками) пяти плюсневых костей и выступом пяточной кости. Определение распределения нагрузки для этих шести областей является объектом отдельного исследования. Отметим только один факт, что при наличии большого числа научных работ, посвященных этому вопросу, полученные результаты сильно отличаются не только у разных исследователей, но и в рамках одного исследования [14, 15, 16, 17].

Введем следующие обозначения:

O - центр вращения голеностопного сустава.

XDY - неподвижная система координат, связанная со стопой.

EOA - сегмент, при помощи которого моделируются сразу две кости - пяточная и таранная. Эти кости представлены в виде одного тела в силу их малой подвижности друг относительно друга.

AB, BC, CD - сегменты, отвечающие за ладьевидную, клиновидную и плюсневую кости стопы, соответственно.

F i ( i =1..2), T - мышечные силы, действующие в данной рассматриваемой части стопы, F i - силы имеющие одну точку крепления на стопе, а другую вне ее, T -отвечает за мышцу (plantar aponeurosis ), оба конца которой крепятся на стопе.

• Y_O, X_O, M 0 - реакции и момент в голеностопном суставе

• Y d , X_D, M D - реакции и момент, приложенные к головке плюсневой кости.

• x i , y_t ( i = 1,4 ) - координаты центров масс каждого из сегментов стопы.

Будем рассматривать стопу как шарнирно-соединенную систему твердых тел. Пять аналогичных друг другу продольных сводов стопы заменим одним. Схема стержневой модели стопы представлена на рисунке 2. Чтобы в дальнейшем перейти к трехмерной модели, необходимо будет рассмотреть все пять продольных сводов стопы, учесть их взаимное расположение и влияние друг на друга.

Предположим, что нам известны условия нагружения свода стопы, тогда необходимо определить:

• 1.    какие при заданных внешних усилиях должны быть усилия в мышцах и связках, 2. как при данных условиях нагружения будет менять свою форму свод стопы.

Иными словами, мы хотим при заданных усилиях Y O , X O , Y D , X D и моменте M D найти углы e i ( i = 1,4 ) , определяющие конфигурацию свода стопы, усилия F 1 , F₂, T и моменты M_n, M., M_R, M_r , R,, R„, R_r .

O A B C ABC

Уравнения движения свода стопы можно получить аналогично уравнениям (2), но тогда будут исключены межзвенные реакции, которые необходимы для нахождения напряжений в связках. Поэтому для решения поставленной задачи рассмотрим сегменты стопы EA , AB , BC и CD по отдельности и для каждого выделенного сегмента запишем уравнения движения.

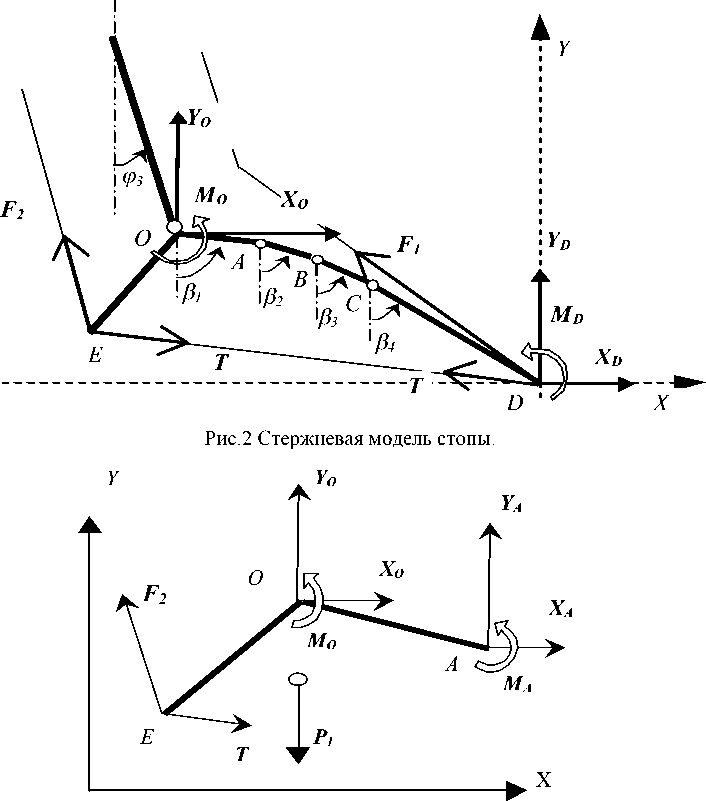
Рис.3. Стержневая схема сегмента EA стопы.

На рисунке 3 изображен сегмент ЕА , который включает в себя пяточную и таранную кости стопы. Для этого сегмента получим следующие три уравнения:

сегмент ЕА mi X i = F2x + Xo + Xa + T,(3)

m 1 yx = —Px + F2y + Yo + Ya + Ty,(4)

L £. = MA + Mo + MF + MR + MR + MT •(5)

1 • 1         a         0         F2         Ra         Ro         Tv /

Здесь m1 и P1 - суммарные масса и вес пяточной и таранной костей, M р , M„ , MT, М„ - моменты, создаваемые силами F?, R , Т и Ro относительно F2 7 Ra 7 T 7 Ro                      7                                                   л центра масс сегмента EA .

Величины моментов MA, M0 и силы T зависят от свойств соединительной ткани. Вопрос построения определяющих соотношений для мягких тканей (мышц, связок и сухожилий) в данной работе не рассматривается. На сегодняшний день имеется огромное количество определяющих соотношений от простых соотношений теории упругости до соотношений, в которых учитываются происходящие в мягких тканях химические процессы. На наш взгляд, выбор вида определяющих соотношений должен обуславливаться целью исследования. В первом приближении мы будем использовать определяющие соотношения теории упругости для моментов MA, M0 , а также Mn, Mr .

BC

Величину силы Т также будем считать подчиняющейся упругому закону:

- L L °

V L 0   7

T = E T

, где L, L 0 - текущая и начальная (в недеформированном состоянии)

длина отрезка, соединяющего точки Е и D (рис.2), E T - модуль упругости. Впоследствии предполагается использовать более сложные определяющие соотношения, учитывающие вязкоупругие свойства тканей, например, такие как предложены в работе Фанга [18].

Аналогично тому, как было сделано для сегмента ЕА , запишем уравнения движения для оставшихся частей стопы:

сегмент АВ m2X2 = Xb — XA ,

^m2 y 2 = — ^P2 ^{+ Y}B

Y a , R + M R_A

—

L в =- M. + Mr + M

2i 2          A B

RB ^

сегмент ВС m, X, = Xr — Xh , 33 C B m3 y 3 =— P3 + Yc — Yb ,

L в =— Mr + Mr + Mp + M„ , 3» 3          в c       Rb        Rc ~ сегмент СD

ID в = — M С + M P + M D + M P • d 4 /4          c      R c       d      P 4

Данная система уравнений (3)-(12) получена в предположении, что в данный момент времени нет контакта пяточной кости с поверхностью, в результате чего в последних трех уравнениях этой системы отсутствует сила F1, которая отвечает за поднятие носка стопы.

Из системы уравнений (3)-(12) можно временно исключить все внутренние реакции в суставах, проекции силы F2 на оси X, Y и ускорения центров масс с помощью кинематических соотношений. Замкнутая система уравнений получается после добавления соотношений для координат точки О:

Хо(t)= Pix(j i,j = 14,(13)

Уо(t)= Piyв) i,j = 14.(14)

После чего мы получим следующую систем у дифференциальных уравнений для определения изменения неизвестных углов в i ( i = 1,4 ) :

Г»О а11в 1 + a12Р2 + a13Р3 + a14Р4 = fl,

О» О» О»

a22Р2 + a23Р 3 + a24Р 4 = f2 ,

»»»»

a33Р 3 + a34Р4 = /з , a44Р4 = f4.(18)

где коэффициенты aij являются функциями масс-инерционных характеристик стопы и углов Рi, fi - функциями заданных усилий YO, XO, YD, XD, момента MD, углов Рi и xO (t), Уо (t). Полученная система (15)-(18) интегрируется численно при соответствующих начальных условиях.

Математическая модель повреждаемости

Одной из причин травм в мягких тканях в медицинской литературе называется асимметричная быстроменяющаяся нагрузка. Любые мышцы состоят из пучков поперечно полосатых волокон [19]. В типичной мышце с параллельно расположенными волокнами каждое из волокон идет по всей ее длине. На обоих концах волокна прикрепляются к элементам скелета непосредственно или с помощью сухожилия.

Сухожилия построены из пучков волокон, которые состоят из коллагена. Волокна эти расположены параллельно продольной оси сухожилия, благодаря чему механические свойства коллагена приобретают решающую роль в формировании механических свойств сухожилия. Основные из этих свойств - большая прочность на разрыв, гибкость, незначительная растяжимость и эластичность.

Введем параметр, отвечающий за целостность материала ^ - сплошность. Пусть, сначала происходит “хрупкое разрушение” [20] одного из волокон при ψ =0, после чего нагрузка перераспределяется на остальные волокна, для которых 0 i <  1 . Далее происходит последовательное “разрушение” всех остальных волокон мышцы.

Примем, что скорость роста поврежденности определяется эффективным напряжением с _kmax /у (для сокращения записи с _k = ^ _kmax ), т.е.

di f

v V J

.

Рассмотрим более простой случай степенной зависимости dV    4

"dt"

n

"T

V V 7

,

A>0, n > 0 - некоторые постоянные. После интегрирования это уравнение дает при ^ =0

tk =---------------, k A(n +1)" k tk - время “разрушения” волокна при заданной нагрузке. Последовательный разрыв волокон будет определять ступенчатый характер нагрузки (напряжения) для каждого неразорвавшегося еще волокна. Тогда справедлив закон линейного суммирования повреждений, и можно записать (21) в виде [20]:

ⁱ Δ t

Е — = 1, i = 1, N о ,                      (22)

к=1 tik где N0 - число волокон в мышце; tik - время “разрушения” i-ого волокна при действии к-ой нагрузки, то есть отвечающее текущему значению напряжения; Atk - время действия к-ой нагрузки. Последнее выражение есть ни что иное, как система алгебраических уравнений порядка N0 относительно времени последовательного разрушения Atk действия N0 нагрузок. При этом в каждом последующем уравнении на одно неизвестное больше чем в предыдущем, а первое есть уравнение вида

^A t i = t ii

A(n + 1 ) ^ ⁿ_n ’

здесь Oik - напряжение в волокне с номером i (i = 1,к) при количестве неразорвавшихся слоев равном N0 - к (к = 1,N0), к - номер последнего разорвавшегося волокна.

Поэтому возможно получение рекуррентной формулы для вычисления A t i и тогда время разрушения слоя толщиной H определяется следующим выражением

N 0

t = A t i i Y a t,,                                    (24)

i = 2

в котором A t i можно определить из системы (22), а для A t 1 будем использовать (23).

Исследование накоплений повреждений в мышцах в данной работе проводилось на основе анализа состояния этого вопроса в литературе. Все литературные источники, известные авторам работы, которые в той или иной степени касаются рассмотрения этого процесса, носят описательный характер, так как этой проблемой не занимались ни математики, ни механики. В литературе можно встретить анализ причин и механизмов возникновения, накопления повреждений, основанный на наблюдениях лечащих врачей, а также общие рекомендации более рационального проведения тренировок и выполнения различных упражнений на основе практического опыта самих спортсменов.

Предложенная в работе методика оценки повреждений в мышцах позволяет провести сравнительный анализ спортивного упражнения с разными уровнями нагрузок по времени условного разрыва волокон мягких тканей и определение наиболее безопасного выполнения данного упражнения. Количественная оценка времени накопления повреждений возможна после получения из эксперимента констант уравнения повреждаемости (20), что выходит за рамки данной работы.

Численная реализация и обсуждение

Численная реализация предложенной методики проводилась для спортсмена с данными, приведенными в работе [8]. Не имея литературных данных или собственного эксперимента по динамике приземления, авторы провели численный эксперимент при отталкивании гимнаста от жесткой поверхности от полного касания ступни до отрыва пятки на некоторую высоту. Задав простую кинематику, близкую к реальной, получили значение усилий Y_O, X_O, Y D , X D и момента M D . Координаты x_O , y_O точки O входили в заданную кинематику.

Модель нагружения стопы и определение напряжений в мягких тканях рассчитывалась как в статическом, так и динамическом вариантах при начальных условиях полученных выше. Были использованы значения материальных констант приведенные в [11]. Геометрические размеры стопы снимались с натурной модели скелета стопы. Полученные усилия и напряжения близки к литературным экспериментальным [17] и расчетным [11] данным.