Прогнозирование прочности углерод-углеродного эндопротеза головки бедренной кости при статических испытаниях

Число операций по имплантации эндопротезов головки бедренной кости увеличивается с каждым годом. Только в Европе их счет идет на десятки тысяч. Хирург-ортопед может выбрать протезы различных типов и производителей из нержавеющей стали, сплавов на основе кобальта, титановых сплавов и т.д. Однако между металлическими материалами и костью образуется соединительная ткань, что сказывается на работе эндопротезов. Известно, что углерод-углеродные композиционные материала характеризуются биосовместимостью с тканями человека. Они хорошо приживаются, не давая нежелательных реакций. Уже в 1982 г. появилась информация о стержнях тазобедренных суставов из углерод-углеродных композитов, разработанных в Германии [1]. В 80-х годах в Перми в Уральском научноисследовательском институте композиционных материалов Ю.А. Змеевым, Ю.К. Осоргиным, П.Г. Удинцевым были разработаны эндопротезы тазобедренного сустава из композита на основе углеродной ткани. Сотрудниками кафедры травматологии, ортопедии и военно-полевой хирургии Пермской государственной медицинской академии А.С. Денисовым и В.Л. Скрябиным в начале 90-х гг. уже были проведены десятки операций по вживлению углерод-углеродных эндопротезов.

Материал, выпускаемый сейчас под торговым названием CarBULAT ™ , создается одновременно с конструкцией на основе ткани «Урал ТМ/4-22», уплотняемой пироуглеродной матрицей в процессе газофазного осаждения [2]. Продвижение его на рынок европейских стран требует проведения испытаний в сертифицированных лабораториях, в том числе статических испытаний до разрушения по стандарту ISO 7206-5. Отметим, что высокая стоимость материала-конструкции и сертифицированных испытаний делает целесообразным предварительное математическое моделирование напряженно-деформированного состояния эндопротеза и прогнозирование предельной нагрузки для эндопротезов различных типоразмеров.

Схема испытания

Для статических испытаний, проводимых в соответствии со стандартом ISO 7206, образцы эндопротезов готовятся специальным образом. На конус эндопротеза (шейку) надевается стальная головка, представляющая собой шаровой сегмент диаметром 34 мм и высотой 28 мм, в котором выполнено коническое отверстие с конусом Морзе 14x16 мм глубиной 20 мм. Ножка эндопротеза устанавливается в стальной сосуд и заливается смесью на основе эпоксидной смолы и твердого наполнителя таким образом, чтобы расстояние H от центра головки до плоскости заделки было 80 ± 2 мм, углы между осью ножки и вертикалью в двух взаимно перпендикулярных плоскостях составляли 9 ° и 10 ° . Образец выдерживается не менее суток до полного отверждения смолы. Готовый к испытаниям эндопротез показан на рис.1.

На головку эндопротеза при испытаниях сверху накладывается стальная плита с соответствующим шаровым углублением. Схема нагружения в испытательном устройстве приведена на рис. 2.

Рис. 1. Образец для статических и усталостных испытаний

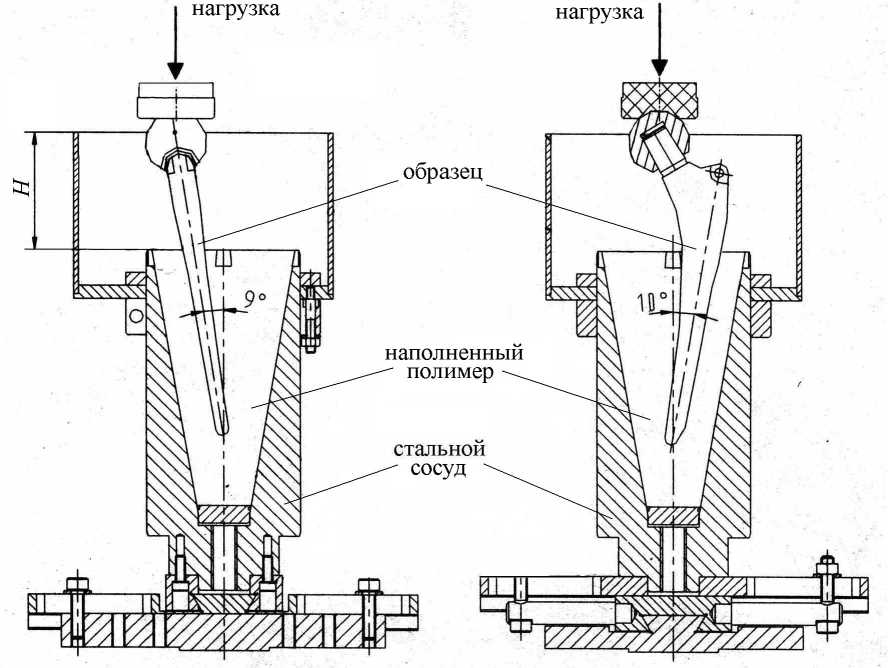
Рис. 2. Схема нагружения эндопротеза в испытательном устройстве

Построение геометрической и конечноэлементной модели статических испытаний эндопротеза тазобедренной кости в пакете ANSYS 5.5

Твердотельная трехмерная модель испытаний эндопротеза сустава тазобедренной кости создана по двумерным проекциям протеза (рис. 3 и 4) на основе схемы нагружения (рис. 2). Поскольку протезы проектируются на различные типоразмеры с определенным диапазоном изменения геометрических характеристик, реализована параметрическая модель вычислительного эксперимента. В качестве базовых параметров конструкции, определяющих ее геометрию, приняты размеры сечений A-A , B-B , высота основания (ножки) и шейки протеза, радиус скругления переходной части и другие размеры (рис. 3 и 4). Работа осуществлена в графическом процессоре пакета ANSYS 5.5.

Модель строилась преимущественно по принципу: точки – линии – поверхности – объемы. Логические операции, такие как вычитание ( OVLAP ), склейка ( GLUE ), разделение ( DIVIDE, SBA ) геометрических примитивов сведены до необходимого минимума, что в данном графическом редакторе обеспечивает большую надежность последующих численных расчетов. Выбираются опорные точки, линии строятся по готовым опорным точкам. Аппроксимация линий по точкам задается прямыми, сегментами окружностей и сплайн–аппроксимациями. Поверхности, если они не лежат в одной плоскости, интерполируются полиномом третьей степени.

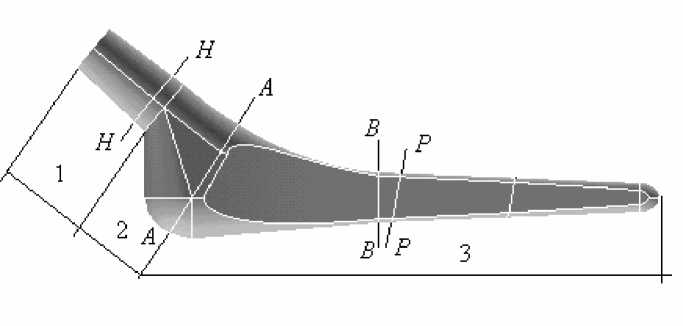
Рис. 3. Фрагменты эндопротеза: 1 – шейка; 2 – переходная часть; 3 – ножка. P-P – сечение поверхностью заделки; H-H – граница контакта с головкой

Рис. 4. Несимметричность эндопротеза: 1 – цилиндрическая поверхность; 2 – плоскость

Построение геометрической модели осуществляется поэлементно. Так, например, отдельно строится верхняя (шейка), переходная, нижняя (основание) части эндопротеза, заделка, нагружающая система. На рис. 3 приведено разбиение эндопротеза на фрагменты для описания его геометрии, на рис. 4 показано задание несимметричности геометрической модели протеза.

Заделка оформляется в виде усеченного конуса, ось основания эндопротеза ориентирована в нем под заданными углами с нормалью к верхней плоскости заделки (9? и 10 ° в двух взаимно перпендикулярных плоскостях, рис. 3). Плоскость площадки, на которой приложена нормальная нагрузка, параллельна плоскости заделки (рис. 5). Величина погружения ножки эндопротеза в заделку может быть различной. Она определяется расстоянием H между точкой С центра сферической головки и плоскостью входа ножки в эпоксидную заделку. Для стандартных испытаний предусмотрено задание H = 80 ± 2 мм. Для исследования влияния условий закрепления в обойме на напряженно-деформированное состояние эндопротеза построены модели и проведены расчеты для двух величин H = 80 мм и H = 56 мм.

Специфика данной задачи заключается в том, что в рассматриваемой конструкции имеет место контакт тел с существенно отличающимися материальными свойствами (заделка – основание эндопротеза, шейка – нагружающая система). Как будет показано ниже, это приводит к значительной концентрации напряжений в локальных зонах. Поэтому принципиальным является вопрос о выборе типа конечных элементов и их числа в особых зонах.

В работе использовались два типа конечных элементов: Solid 45, Solid 92. Первый характеризуется линейной аппроксимацией перемещений и кусочно постоянной аппроксимацией напряжений, второй – квадратичной аппроксимаций перемещений и линейной аппроксимацией напряжений. Выбор того или иного типа аппроксимации осуществлялся из решения серии предварительных задач для рассматриваемой конструкции с разной густотой разбивки.

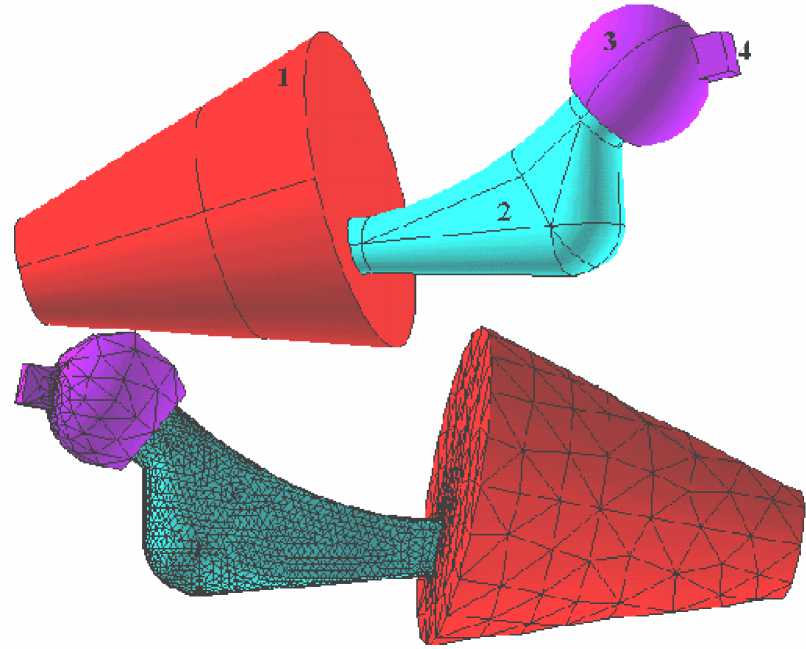
Рис. 5. Твердотельная и конечноэлементная трехмерные модели эксперимента. 1 – заделка, 2 – эндопротез, 3 – стальная головка, 4 – площадка приложения нагрузки

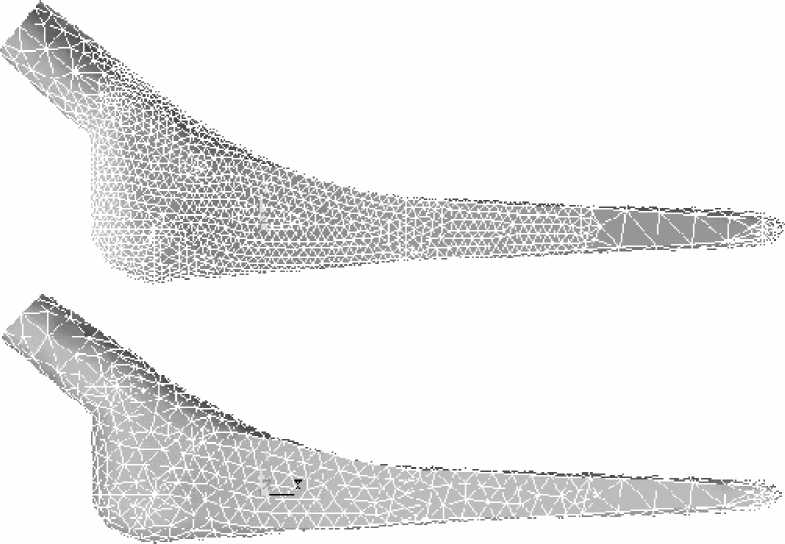
Рис. 6. Примеры конечноэлементных сеток. Число конечных элементов варьируется от

10 000 до 20 000

Таблица

Упругие характеристики материала

E z	E r	E о	G zr	G о r	G о z	v zr	v 0 r	v 0 z
20 ГПа	10 ГПа	17 ГПа	1,6 ГПа	1,6 ГПа	1,2 ГПа	0,125	0,147	0,16

В написанной процедуре разбивки твердотельной модели число конечных элементов, привязанных к какой-либо линии, может варьироваться. На рис. 6 приведены примеры конечноэлементных разбивок с 10000 и 20000 конечных элементов.

Заготовка для эндопротеза сшивается углеродной нитью в виде кокона из нескольких специально выкроенных слоев пропитанного полимерным связующим тканого углеродного материала «Урал ТМ/4-22». Полученную заготовку укладывают в металлическую форму, изгибая таким образом, что направление нитей основы ткани в шейке составляет угол примерно 40 ° по отношению к направлению нитей основы в ножке. После процессов формования и отверждения полимерного связующего заготовка отправляется в установку газофазного осаждения пироуглеродной матрицы.

В расчетах материал конструкции рассматривается как однородный, локально ортотропный, с эффективными свойствами, определяемыми из эксперимента. В расчетах принято, что протез состоит из двух фрагментов, у каждого из которых свое направление оси цилиндрической ортотропии (условно шейка и основание протеза). Эти оси ортотропии направлены под углом 40 ° по отношению друг к другу в соответствии с основным направлением основания и шейки протеза. Граница, делящая протез на участки с разными материальными свойствами, – сечение А-А (см. рис. 3). Упругие свойства материала в цилиндрической системе координат указаны в таблице, где z, r, 0 - направления главных осей цилиндрической ортотропии: z совпадает с осью симметрии, r - радиальное и 0 - окружное направления.

На внешних поверхностях объема заделки задается жесткое закрепление. На верхнюю площадку стального шара прикладывается распределенная вертикальная нагрузка с интегральной величиной усилия 1000 Н. В силу линейности постановки задачи направление нагрузки остается неизменным вне зависимости от ее величины.

Оценка напряженно-деформированного состояния эндопротеза при статических испытаниях на прочность

Результаты расчетов напряженного состояния эндопротеза анализировались в координатных системах, связанных с осями ортотропии отдельно для двух фрагментов, описанных в разделе 2 (фрагмент 1 – в районе шейки и фрагмент 2 – нижняя часть ножки эндопротеза). Особое внимание уделялось характеру изменения полей напряжений в зонах контакта различных материалов на свободных поверхностях.

Существуют две зоны концентрации напряжений: в области контакта стальной головки эндопротеза с шейкой и в области контакта заделки с нижней частью ножки. Результаты различных экспериментов подтверждают наличие в этих зонах наиболее вероятного разрушения. В экспериментах с расстоянием от центра сферы до плоскости входа ножки в заделку H = 80 мм разрушение фиксировалось в окрестности контакта заделки с нижней частью ножки. При испытаниях некоторых образцов с уменьшенным значением H« 50 ^ 60 мм разрушение происходило в окрестности контакта сферической головки и шейки с трещиной на растянутой стороне, имеющей кольцевое направление. На рис. 7 показано распределение осевых напряжений в шейке эндопротеза в эксперименте с расстоянием H = 80 мм.

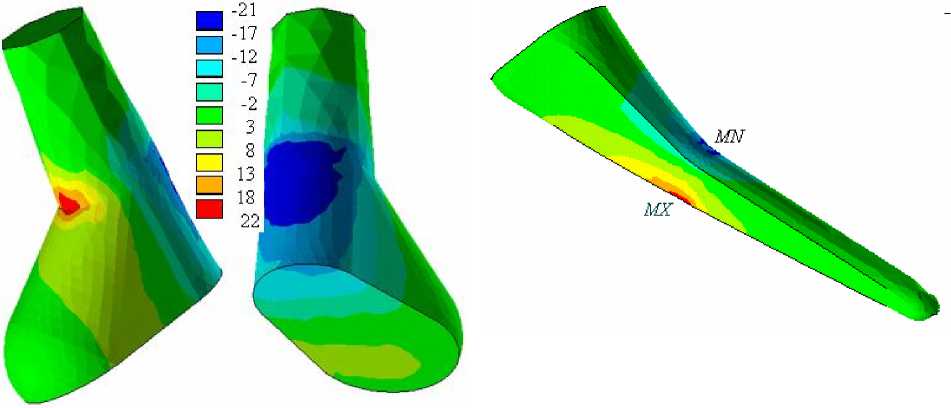
Рис. 7. Осевые напряжения (МПа) в шейке протеза в окрестности контактной зоны

Рис. 8. Зоны концентрации максимальных растягивающих ( MX ) и максимальных сжимающих напряжений ( MN ) в окрестности заделки

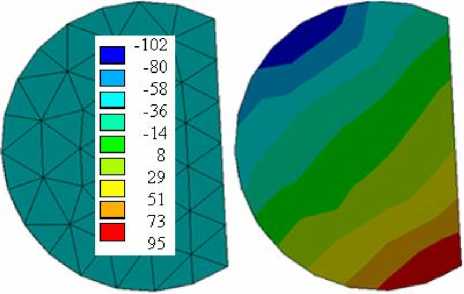
Рис. 9. Осевые напряжения (МПа) в ножке протеза в сечении заделки при H = 80 мм

Максимальные напряжения в ножке эндопротеза возникают в месте входа ее в эпоксидную смолу в направлении основы ткани (практически совпадающего с направлением оси z ). На рисунках 8 – 9 показан характер распределения осевых напряжений в экспериментах с расстоянием точки С от плоскости входа ножки в заделку, H = 80 мм. Другие компоненты тензора напряжений оказываются существенно меньшими по величине, чем осевые напряжения в окрестности заделки.

Анализ осевых напряжений в сечении плоскостью заделки позволяет проанализировать справедливость гипотезы плоских сечений. Оказывается, с достаточной степенью достоверности она может быть принята для рассмотренных вариантов протезов. Об этом говорит распределение осевых напряжений в сечении, поскольку оно достаточно хорошо аппроксимируется линейным законом (рис. 9). На этой основе построена упрощенная методика прочностного анализа эндопротезов.

Контакт основания эндопротеза с полимерной заделкой для рассматриваемой нагрузки вызывает сильную концентрацию сжимающих и растягивающих напряжений. Численный анализ поля напряжений в этой области с использованием конечных элементов разных типов и размеров позволяет утверждать, что в этих местах имеет место особенность для точного решения задачи теории упругости.

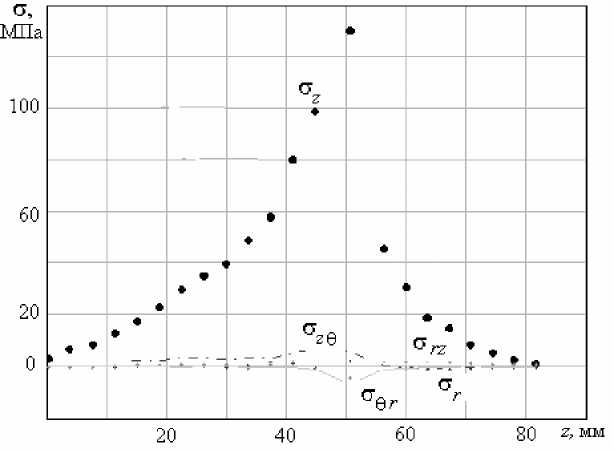
Рис. 10. Зависимость от осевой координаты различных компонент тензора напряжений в окрестности заделки

На рис. 10 показано поведение различных компонент тензора напряжений как функций осевой координаты вдоль ребра нижней части эндопротеза. Видно, что определяющий характер имеют осевые напряжения. С уменьшением размеров конечных элементов увеличиваются максимальные значения напряжений, однако характер зависимости осевых напряжений от координаты не изменяется. Это свидетельствует о возможности прогнозирования прочности конструкции эндопротезов с помощью нелокальных критериев прочности.

Выявленные на основе расчетов в пакете ANSYS закономерности распределения напряжений и деформаций позволили разработать упрощенную методику прочностного анализа эндопротеза из углерод-углеродного композиционного материала на основе подсчета максимальных осевых напряжений по правилам сопротивления материалов. С помощью данной методики произведена оценка прогнозируемой нагрузки разрушения при испытаниях эндопротезов различных типоразмеров.

В качестве исходных данных для расчета были приняты результаты статических испытаний двух образцов эндопротеза с размером L = 157,5 мм. Образцы испытывались на трехточечный изгиб с расстоянием между опорами 120 мм [3]. По данным этих испытаний были рассчитаны максимальные растягивающие a + max и максимальные сжимающие a max напряжения в осевом направлении (по отношению к осям, связанным с тканевым материалом, - в направлении основы): a + max = 216 ^ 230 МПа; a _max = 235 ^ 250 МПа. Принимая рассчитанные растягивающие напряжения в качестве предела прочности материала эндопротеза при растяжении, можно оценить предельную нагрузку при испытаниях эндопротеза любого типоразмера и на внецентренное сжатие в обойме по стандарту ISO 7206-5.

В частности, для эндопротезов того же типоразмера предельная нагрузка, рассчитанная вышеуказанным образом, оказалась равной 3,0^3,2 кН. Однако экспериментальные данные для этой нагрузки, полученные на шести образцах [4] данного типоразмера, показывают существенно большие величины нагрузки: 4,7; 4,72; 4,93; 5,25; 5,98; 4,55 кН (среднее значение нагрузки 5,0 кН, коэффициент вариации 10%). Расхождение расчетной и экспериментально определенной предельной нагрузки обусловлено существенно различными условиями работы конструкции в этих двух видах испытаний. При трехточечном изгибе нагрузка сосредоточена на очень малой площадке, что приводит к повреждению поверхностных слоев. В этом случае механизм разрушения несколько отличается от механизма разрушения в условиях испытаний на внецентренное сжатие в обойме по стандарту ISO 7206.

Поэтому целесообразно оценивать разрушающую нагрузку при испытаниях на внецентренное сжатие в обойме для образцов различных типоразмеров только по результатам аналогичных испытаний образца эндопротеза одного из типоразмеров.

Рассчитанные по средней по 6 образцам разрушающей нагрузке в испытаниях на внецентренное сжатие в обойме образцов с размером L = 157,5 мм максимальные напряжения составляют: σ ⁺ max = 420 МПа; σ ^– max = 390 МПа. Принимая рассчитанные растягивающие напряжения в качестве предела прочности материала эндопротеза при растяжении, получим расчетное среднее значение разрушающей нагрузки 3,8 кН для образцов эндопротеза с размером L = 151 мм и 6,6 кН для образцов эндопротеза с размером L = 162,5 мм.

Итак, попытки использовать в качестве константы максимальные растягивающие напряжения, определяемые из проведенных испытаний на трехточечный изгиб эндопротезов, показывают заниженные значения предельной нагрузки по сравнению с экспериментом. Необходимо определять «прочностную константу» материала (предел прочности в направлении основы ткани при растяжении) из испытания в обойме образца эндопротеза одного из типоразмеров.

Выводы

Разработана геометрическая модель эндопротеза в пакете ANSYS 5.5, выбрана схема конечно-элементной дискретизации геометрической модели. В пакете ANSYS 5.5 произведены расчеты напряженно-деформированного состояния эндопротеза с учетом анизотропии материала при схеме нагружения, использованной в статических и усталостных испытаниях эндопротезов.

Исследовано влияние условий нагружения и закрепления эндопротеза на напряженно-деформированное состояние и статическую прочность конструкции в испытаниях. Проведен анализ распределения напряжений и деформаций и обоснована упрощенная методика расчета предельной нагрузки в испытаниях.

Проведены расчеты напряженного состояния и предельной нагрузки для различных типоразмеров эндопротезов. Результаты проведенных исследований показывают, что для обоснованной уточненной оценки поведения эндопротезов в бедренной кости необходима экспериментально-теоретическая разработка новых критериев предельного состояния тканевых углерод-углеродных композитов.

Благодарности

Авторы благодарны Михаилу Готесману за организацию экспериментальных исследований и сотрудникам университета г. Мишкольц (Венгрия) Ласло Шентпетери, доктору Иштвану Галу, профессору Миклошу Тише за проведение испытаний эндопротезов.