Прогнозирование развития предприятия по переработке плодово-ягодного сырья с помощью модели регрессионного анализа

Рост конкуренции в реализации энерго-и ресурсосберегающих технологий XXI века, изменение предпочтений покупателей на основе изменений совместного действия спроса и предложения, трудности с реализацией выпускаемой плодово-ягодной продукции и многое другое вынуждают современные аграрные компании искать новые идеи для роста прибыли и снижения совокупных производственных затрат. В отраслях переработки плодовоягодного подкомплекса АПК наблюдается тенденция спада производства. На переработку поступает всего около 20 % валового сбора плодов и ягод. В структуре выпускаемой продукции переработка плодов и ягод на консервы составляет более 90 % и лишь 0,5 % подвергается быстрой заморозке и идет на производство сухофруктов.

В Воронежской области имеется хорошая сырьевая база для производства плодово-ягодных консервов, но для обеспечения наиболее эффективной деятельности заводов необходимо осуществлять планирование производства. Наиболее сложным методом прогнозирования является прогнозирование на основе взаимосвязанных рядов динамики. С его помощью можно получить не только оценки результативного, но и факторных признаков, т.е. результаты анализа взаимосвязанных рядов динамики выражаются с помощью системы уравнений регрессии. Прогноз в этом случае лучше поддается содержательной интерпретации, чем простая экстраполяция. Нормативный метод

прогнозирования заключается в установлении для определенного отрезка времени фиксированной системы норм. В качестве инструмента при нормативном прогнозировании могут быть использованы теория графов, матричный подход и др.

Сущность целевого прогнозирования заключается в решении обратной задачи: в отыскании условий для достижения в будущем норм, задаваемых в виде строго определенных и обоснованных величин. Решение этой задачи обычно осуществляется методами математического программирования.

Комплекс методов прогнозирования постоянно совершенствуется и пополняется новыми методами. Однако классификация прогнозов по методам их разработки затрудняется отсутствием единой классификации методов. Наиболее важными классификационными признаками методов прогнозирования являются следующие: степень формализации, общий принцип действия, способ получения прогнозной информации.

По степени формализации методы прогнозирования можно разделить на интуитивные и формализованные. Интуитивные применяются, когда невозможно учесть влияние многих факторов из-за значительной сложности объекта прогнозирования, либо когда объект слишком прост. Эти методы базируются на информации, которая получена на основании оценок специалистов-экспертов. Формализованные методы базируются на фактически имеющемся информационном материале об объекте прогнозирования и его прошлом развитии.

Классы интуитивных и формализованных методов прогнозирования по своему составу аналогичны экспертным и «фактографическим». Фактографические методы имеют источник информации об объекте прогнозирования, основанный на фактических данных, необходимых для достижения цели прогнозирования; экспертные – базируются на информации, полученной по оценкам специалистов-экспертов.

Применим регрессионные модели для прогнозирования выпуска яблочного повидла. Планируемый объём реализации яблочного повидла на СХА «Аннинская» представляет собой временной ряд из 6 уровней (табл. 1).

Т а б л и ц а 1

Исходные данные по объему яблочного повидла (тыс. р.)

Дата	07.09	08.09	09.09	10.09	11.09	12.09
Объем реализации	251,32	268,30	271,45	271,45	283,24	283,24

Динамика развития во времени дана на рис. 1.

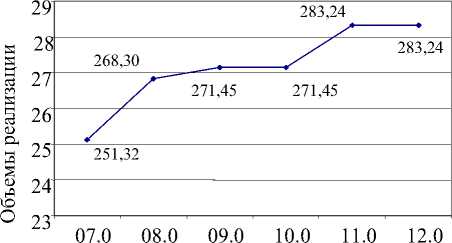
Дата

Рис. 1. Динамика объемов продаж

В общем виде при исследовании экономического временного ряда x _t выделяют несколько составляющих:

xt = ut + vt + ct + ^t (t = 1,2,..., n), где ut - тренд, плавно меняющаяся компонента, описывающая чистое влияние долговременных факторов, т.е. длительную тенденцию изменения признака; vt - сезонная компонента, отражающая повторяемость экономических процессов в течение не очень длительного периода; ct -циклическая компонента, отражающая повторяемость экономических процессов в течение длительных периодов; Et - случайна компонента, отражающая влияние не поддающихся учету и регистрации случайных факторов [1].

Одна из задач исследования временного ряда – выделение основной тенденции изучаемого процесса, выраженной неслучайной составляющей, тренда.

Для решения этой задачи чаше всего используются функции:

линейная: u (t) = b 0 + b1t;

полиноминальная:

u (t) = bo + bit + b 2t2 +... + bntn;

экспоненциальная

u ( t ) = e^b o ^{+ bt};

логистическая

u ( t ) =

a

1 + be ~^et

Рис. 2. Интерфейс аналитической программы

Выберем для исследования линейную зависимость. Предварительно проведем анализ временного ряда с помощью коэффициента детерминации. Для этого воспользуемся пакетом «Анализ данных» в электронных таблицах Exsel (рис. 2) [2].

Т а б л и ц а 2 Данные расчетов, выполненных в пакете «Анализ данных»

Регрессионная статистика
Множественный R	0,928038944
R-квадрат	0,861256282
Нормированный R-квадрат	-1,5
Стандартная ошибка	4,903258975
Наблюдения	1

В соответствии с полученными результатами определился коэффициент детерминации R ² = 0,8613 (табл. 2).

Его значение показывает, что вариацию реализации ( y ) можно практически полностью объяснить влиянием включенного в модель временного ряда. На долю остальных неучтенных в явном виде факторов приходится 14 % вариации выходной функции. Такую же величину нам показал и тренд линейного типа (рис. 3).

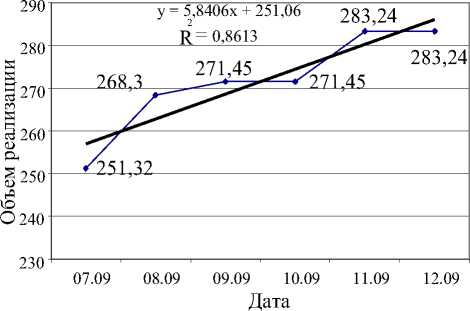
Рис. 3. Динамика развития во времени с добавлением линейного тренда.

Уравнение регрессии и коэффициент детерминации выведены на (рис. 3). С помощью полученного уравнения можно сделать прогноз объемов реализации на следующую отчетную дату (рис . 4):

y = 5,8406 • 7 + 251,06 = 291,7 тыс.р.

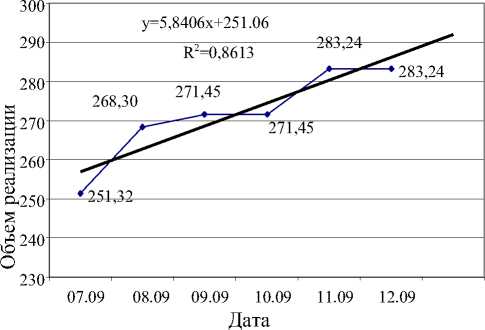
Рис. 4. Прогноз объемов реализации

Применив полиноминальную функцию для построения прогноза, получим объемы реализации на следующую отчетную дату (рис. 5). Данный вид тренда гораздо лучше описывает тенденцию развития процесса, имеет коэффициент детерминации R ² = 1 , т.е. в нашем случае идеально учитывает влияние факторов. Но если посмотреть на аналитический вид уравнения, то коэффициенты функции носят сложный характер, поэтому 186

прогнозирование в значительной мере затрудняется.

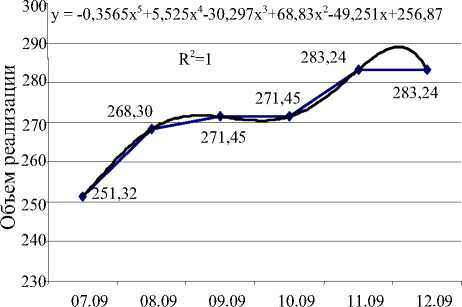
Дата

Рис. 5. Динамика развития во времени с добавлением тренда полиноминального типа

Не исключена и вероятность риска, так как сок прямого отжима рассчитан на покупателя с высоким уровнем дохода. На Западе соки прямого отжима на 35-50 % дороже восстановленных, но такая разница в цене вполне обоснована. [1] Важным фактором риска являются и неблагоприятные климатические условия, так как урожаи ежегодно значительно отличаются, а следовательно, и объем производства может не соответствовать запланированному.