Прогнозирование развития сельскохозяйственных культур в цифровом двойнике посевов растений

Эффективное управление растениеводством важно для повышения урожайности, снижения затрат и минимизации вреда для окружающей среды. Разработка методов адаптивного планирования и моделирования стадий роста и развития растений, прогнозирования урожайности актуальны и значимы для продуктивности и эффективности растениеводства.

Одной из ключевых культур для Российской Федерации является пшеница [1]. Масса собранной озимой пшеницы в Самарской области за период с 2013 по 2023 годы составляла от 606 тыс. тонн до 1374,4 тыс. тонн, в т.ч.: в 2017 году – 1321,4 тыс. тонн, в 2018 году – 880,5

тыс. тонн, в 2019 году – 709,1 тыс. тонн, в 2020 году – 1633,6 тыс. тонн 1 . Приведённые сведения показывают значительные изменения массы собранного зерна в зависимости в т.ч. от погодных условий.

Прогнозировать урожайность средствами, применяемыми агрономами и фермерами, трудно в силу отсутствия адекватных математических моделей физиологии растений и среды. Многие сорта сельскохозяйственных (с/х) растений являются искусственно созданными и постоянно обновляются. Это не позволяет собрать большие объёмы данных и провести статистически значимую обработку данных в различных условиях, чтобы построить точные и достоверные модели. Большой вклад в процессы роста и развития растений вносят технологии агрономической обработки семян, растений и почвы полей, отчасти компенсирующие неблагоприятные факторы внешней среды.

Кроме неопределённости и колебаний погодных условий, трудности прогнозирования роста и развития с/х культур являются следствием недостаточности агрометеорологических наблюдений сети гидрометеостанций на производственных посевах [2]. Обычно на практике применяют анализ данных дистанционного зондирования Земли [3]. Анализ этих данных в ряде случаев является достаточным для мониторинга (и отчасти прогнозирования) роста и развития посевов на больших территориях, но для управления хозяйствами необходимы более точные модели роста и развития растений, позволяющие вести достоверное прогнозирование и рассчитывать влияние факторов внешней среды на выходные параметры растений.

Значительный прогресс достигается применением технологий Интернета вещей для мониторинга погоды и фактического состояния растений и почвы [4]. Однако задачу моделирования и прогнозирования роста и развития посевов эти средства не решают.

Для поддержки принятия решений агрономами и фермерами традиционные математические модели и статистические методы обработки данных, а также существующие информационные технологии оказываются применимы лишь частично. Становится актуальной задача разработки новых подходов, которые можно на практике легко и быстро адаптировать к климату региона, сортам выращиваемых растений, особенностям полей каждого хозяйства и т.д. Методы и средства моделирования и прогнозирования развития с/х культур должны способствовать повышению эффективности использования доступных ресурсов (вода, удобрения и средства защиты растений), поддерживать подходы точного земледелия, иметь низкую стоимость, быть удобными и простыми на практике.

1    Постановка задачи

Предлагаемый подход заключается в разработке цифровых двойников (ЦД) посевов растений (ЦДПР), которые должны позволять: отражать состояние растения на поле по определённому агрономами ряду важнейших параметров, характеризующих растение на каждой стадии; планировать рост и развитие растений на основе правил принятия решений, формируемых агрономами; моделировать поведение растений при различных событиях и условиях внешней среды; адаптивно перестраивать планы ухода за растениями при наступлении факта или других непредвиденных событий [5].

В настоящей работе развиваются научные исследования, выполняемых в Молодежной лаборатории ЦД растений СамНЦ РАН и в СамГТУ по проектам интеллектуальных кибер-физических систем управления точным земледелием и ЦД брокколи [6]. В работах [7, 8] представлены базовая концепция ЦД растения, методы, модели и средства её построения, реализовано несколько версий ЦДПР, которые проходят испытания на экспериментальных

1 Территориальный орган Федеральной службы государственной статистики по Самарской области.

полях по выращиванию пшеницы и других растений в СамНЦ РАН. Предлагаемые модель и метод расчёта являются основой построения новой версии ЦДПР, базирующейся на основе экспертных знаний агрономов для принятия решений по расчётам зависимостей входных и выходных параметров посевов растений на каждой стадии их роста и развития и более сложной модели растения с внутренним гомеостазом.

Требуется разработать метод расчёта длительности стадий роста и развития посевов растений, а для каждой стадии – метод расчёта значений выходных параметров в зависимости от значений входных параметров, учитывающих состояние окружающей среды и растения. Для разных с/х культур состав входных и выходных параметров на разных стадиях различен, поэтому разрабатываемый метод должен предполагать возможность изменения состава, типов и числа входных и выходных параметров.

По условиям задачи для каждого сорта с/х культуры в онтологии растениеводства задан процесс роста и развития посевов растения на стадиях, состоящий из списка стадий Рго се ss = {s t ад е _i }, i = 1, Lr где L - количество стадий или фаз². Для каждой фазы задан пополняемый список входных и выходных параметр ов, а также параметр длительности фазы.

Для каждой стадии вводятся: Ini = { т^}, j = 1, Кг где K - количество влияющих факторов для i -ой стадии развития с/х культуры. О и ti = {out_{i к}}, к = 1, М, где M - количество выходных параметров для i -ой стадии развития с\х культуры.

Выходные значения одной стадии могут являться входными для следующей:

Ini ₊i с О и 11. (1)

Для каждого сорта растений на основе онтологии растениеводства создаётся онтологическая модель сорта, которая включает семантическую сеть входных и выходных параметров стадий растений. Онтологическая модель сорта растения считается заданной для разрабатываемой системы, куда она загружается в виде json файла.

На рисунке 1 изображена примерная схема связей между параметрами стадий, задающая входные условия для решения задачи.

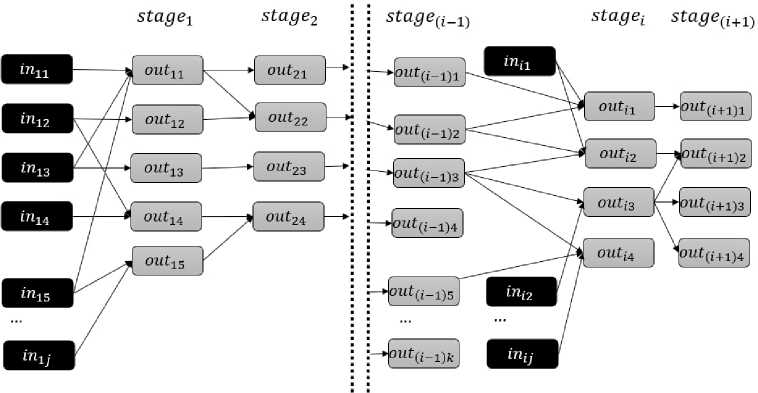
– входные параметры,     – выходные параметры на фазах

Рисунок 1 – Примерная схема условий задачи

На фазе       поступают на вход некоторые входные параметры , такие как темпера тура окружающей среды, или некоторые выходные параметры стадии st дде ( i _ г ). На выходе стадии stадet рассчитываются выходные параметры растения out.. Некоторые из этих выходных параметров стадии stадеi являются входными параметрами для стадии stад е( t+г).

Необходимо разработать метод расчёта параметров посева, который бы не зависел от числа фаз роста растения, а также состава, числа и типа их входных и выходных параметров; требуется обеспечить адаптивность пересчёта параметров фаз при появлении незапланированных событий, связанных с изменениями параметров, например, факта изменения погоды или факта внесения удобрений в почву.

В данной работе в качестве примера рассмотрены стадии роста и развития озимой пшеницы, которые представлены в [9]. Целью разработки является создание модели растения и метода расчётов, которые могли бы применяться для любых злаковых растений.

2    Анализ актуальных методов

Для решения задачи прогнозирования роста и развития растения могут быть использованы разработки в области машинного обучения (МО), в частности, глубокого обучения (ГО), которые показали свои преимущества в решении различного рода задач [10].

В статье [11] использованы методы МО и ГО для прогнозирования урожайности и вариации роста растений. Значения урожайности, роста и диаметра стебля, условия микроклимата используются архитектурой рекуррентной нейронной сети для моделирования целевых параметров роста. Такие модели с МО разрабатываются для использования на разных сортах растений (см., например, [12]). МО предоставляет удобные инструменты для анализа сложных с/х наборов данных при их наличии. Модели с МО на основе изображений могут выявлять болезни растений и заражение вредителями на ранних стадиях, анализировать погодные условия и состояние почвы для прогнозирования урожайности.

Методы МО имеют определённые ограничения [13], особенно при недостатке массивов данных для обучения, а также применении методов МО в условиях неопределённости, когда исходная ситуация, при которой были собраны наборы данных для обучения, изменяется трудно предсказуемым образом. В современных хозяйствах получение точных и полных данных затруднено из-за отсутствия соответствующих инструментов измерений, изменчивости условий окружающей среды и ошибок сбора данных. Низкое качество или недостаточное количество данных могут привести в МО к неточным прогнозам и ненадёжным результатам. Для многих моделей МО, таких как машины опорных векторов и случайные веса, требуются значительные вычислительные ресурсы для обучения и оптимизации, а также специальные знания для настройки и интерпретации результатов. Если обучающие данные, используемые для МО, содержат смещения, то модели могут усилить эти смещения, что приведёт к искажению прогнозов.

В [14] представлен ЦД в с/х производстве. Путём создания начальной цифровой среды для киберфизической системы фермеры могут лучше представлять состояние своих ферм в отношении использования ресурсов и оборудования. ЦД может представлять собой инструмент для оптимизации производительности, как соотношения между производством и потреблением ресурсов [15]. ЦД можно рассматривать как новую фазу интеллектуального развития и управления данными в садоводстве и в сельском хозяйстве в целом [16, 17].

3    Метод расчёта параметров посева

Предлагаемая онтологическая модель роста и развития посевов растений состоит из взаимосвязанных стадий роста и развития растений, где число стадий может быть переменным для разных культур, а также число входных и выходных параметров на каждой стадии может варьироваться, например, высота растения, число зёрен в колосе, площадь листьев, объём урожая и т.д.

На каждой фазе развития на растения влияют факторы окружающей среды, такие как температура воздуха или почвы и запас питательной влаги в почве. Значения факторов на определённых фазах развития растения являются входными параметрами модели. Правила принятия решений для планирования переходов между состояниями стадий также индивидуальны для каждого сорта культуры.

На основе экспертных знаний агрономов выделены составы и значения входных и выходных параметров на разных фазах развития растения x ij_k и составлены трубки входных параметров. Трубкой параметров называются диапазоны изменения значений каждого фактора, влияющего на развитие растения. Наилучшие возможные значения параметров роста и развития растения на каждой фазе считаются оптимальным значениями.

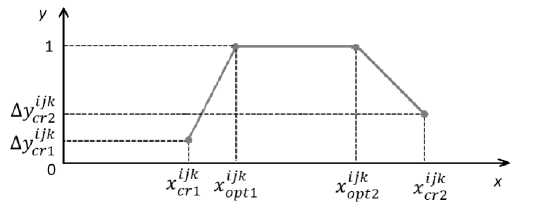
Рисунок 2 - Пример трубки входного параметра x и выходного параметра у

На рисунке 2 показан пример трубки входного параметра х и выходного параметра y, состоящей из четырёх точек: критического мини-ijk мума , рекомендованного мини-ijk мума     , рекомендованного мак- ijk симума     , критического макси- ijk мума      входного параметра для каждой фазы и соответствующим им значений прироста выходных пара- метров ^ylc3rk1, by Optn Ьу0р2, Ду^.

Для нормального развития растения необходимо, чтобы значения входных параметров X[j_k находились между рекомендованными минимумом и максимумом. Если значения входных параметров выходят за критические границы, то растение погибает.

Модель состоит из набора фаз развития растения, которые включают набор трубок входных параметров.

На основе описанной модели разработан метод расчёта выходных параметров растения. Перед расчётом значений выходных параметров необходимо провести расчёт длительности фаз растения. Базовая длительность рассчитывается по правилу суммы активных температур:

duration mQx

durati о n base i = £y=1         1, если ^m i ii < 'j < ^m a x и t a c t jj - 1 ) + ' < t a c ,-> где taсt - сумма активных температур, taсtj__ г) - сумма активных температур за j-1 дней.

На базовую длительность фазы растения влияет предыдущее растение, росшее на месте растения модели, и входные параметры на фазе. Приращение (дельта) длительности i -ой фазы для k -ого входного параметра:

		⎧	0, если	xu к <  x
			x cr 1 )(ду0 p t 1	- byC^
			ijk       ijk X .. — X . ^optl ^crl
Д duratio nik =		(x ij ' к —	xlJkyAvlJk - x о p t 1 )(луо p 12 ijk       ijk ^opt2 ^optl	Д
			-xiJk VAviJk - x o p t 2 )(Ду cr 2	△ y Oj^ )
		⎩	ijk      ijk ^0x2   ^opt2

^{+ Д}уХ если ^ХСГ1 <  ^Xl iк < X^t Г

⁺ &y ^lopt 1 , если ^xopt 1 <  ^хик <  ^х 0 pt₂ ;

ijk              . ijk

'cr i или x у _к >  хГ ₂;

⁺ ^t 2 , если ^хOPt 2 < Х Jк <  ^хГ2

Итоговая длительность i -ой фазы развития растения рассчитывается как сумма базовой длительности фазы d иг ati оп _{aas е t} , дельты длительности влияния предыдущего растения △ Urratiоп_рр i и среднеарифметической суммы дельт длительности i-й фазы для k-ого входного параметра.

Формула расчёта итоговой дельты i -ой фазы развития растения:

к dur ati о n t = urr ati о n base t + △ urr ati о npp i+- ^ △ urr ati о n tk.

y=l

Итоговая длительность должна быть между минимальной и максимальной длительностями:

durat 1ощ =

dur a ti о u_m i_n ,

. dur и t i о um ax,

если durationi <  duration_min; durati оn _t ;

если Uuaationt > Uuaation_max.

После расчёта длительности фаз развития производится вычисление выходных параметров растения. Для этого берутся значения входных параметров с полей за весь период развития растения, разделённые и сгруппированные по предполагаемым периодам фаз. Далее рассчитываются выходные параметры за первую фазу.

Каждую длительность фазы можно разбить на интервалы нахождения растения в определённом состоянии.

Формула трубки параметров k -ого выходного параметра на i -ой стадии для l -ого входного параметра на q -том интервале состояния растения:

tub e[_k = { tubettem^l^}, I = 1,L,q = 1, Q ,

где L - количество входных параметров, влияющих на k -ый выходной параметр на i -ой стадии, Q - количество интервалов в трубке.

tub el tem‘_k = {tubeB о udrr^ , tubeBrudrr^ ⁺ )\ de Ita 0 и tValue‘_kJ. de I ta 0 и tValue ^l_ik = { de11a 0 и tVaIee ^l_k^p},p = 1, P,

где P - количество интервалов длительности влияния.

Итоговое значение дельты выходного параметра на фазе равняется сумме изменений этого выходного параметра на интервалах непрерывного вхождения в интервал трубки. Прирост выходного параметрах в рамках одного интервала трубки равен:

.  , deltaOutValue* ,    _

△ uu t_is =-------------_:---- interval!) rratio n_is.

stageDurationi

△ о и ti = >  △ o и t _ls .

Дельта выходного параметра складывается с итоговым значением на предыдущей фазе, и результатом вычисления является итоговое значение выходного параметра на фазе. Далее происходит расчёт выходного параметра для следующей фазы.

Предложенный метод расчёта выходного параметра представлен в виде псевдокода алгоритма.

Input: phases - список фаз, input_value_list - список входных значений по фазам

Output: output_parameters_set - список, содержащий списки выходных параметров по фазам

1:

2:

3:

4:

5:

6:

7:

8:

9:

10:

previous_phase_value = 0

output_parameters_set = []

plant_alive = true for phase in phases do output_parameters = phase.output_parameters output_parameters_list = []

for output_parameter in output_parameters do input_parameters = output_parameter.input_parameters phase_deltas = []

for input_parameter in input_parameters do

11:

12:

13:

14:

15:

16:

17:

18:

19:

20:

21:

22:

23:

24:

25:

26:

27:

28:

29:

30:

31:

32:

critical_range = get_critical_range(input_parameter, input_value_list[phase])

break end if average_delta = calculate_average(phase_deltas) output_value = average_delta + previous_phase_value output_parameters_list add output_value previous_phase_value = output_value end for output_parameters_set add output_parameters_list end for return output_parameters_set

Работа алгоритма начинается с ввода значений входных параметров для всех фаз согласно длительности фаз, которая рассчитывается по формулам 2-5. В алгоритме на каждой фазе (4) для каждого выходного параметра (7) сравниваются введённое значение с соответствующей трубкой этого входного параметра (13-14): если значение выходит за критические значения трубки, то растение погибает (15); если нет, то происходит расчёт дельты выходного параметра (18) по формулам 6-9. Далее происходит расчёт среднего значения дельты выходного параметра по всем входным параметрам (25) по формуле 10. Итоговое значение выходного параметра рассчитывается как сумма среднего значения выходного параметра и значения на предыдущей фазе (26). В результате полученные значения выходных параметров растения для каждой фазы добавляются в список (30).

4    Пример применения метода

Рассмотрен пример расчёта выходного параметра высоты растения на двух первых фазах развития при четырёх входных параметрах для с/х культуры «Озимая пшеница». Первые две фазы развития – это прорастание и развитие листьев; входные параметры: температура воздуха, содержание нитратов в почве, содержание фосфора и калия в почве.

На вход поступает набор входных параметров, это список пар значение - дата (период с 1 сентября 2023 по 31 августа 2024 года). Датой посева является 5 сентября 2023 года. По формулам 2-5, согласно сумме активных температур, первая фаз длится с 5 по 11 сентября, период второй фазы – с 12 по 26 сентября. На фазе прорастание для расчёта выходного параметра высоты растения берутся значения входных параметров за период с 5 по 11 сентября, после чего по формулам 6-9 происходит расчёт выходного параметра для каждого входного параметра, т.е. для входного параметра температуры воздуха значение выходного параметра высоты растения равно 2.9 см, а для параметра содержание нитратов в почве равно 5 см, для параметров содержание фосфора в почве и содержание калия в почве значения выходного параметра равны также 5 см. Из получившихся значений, а именно 2.9 см, 5 см, 5 см, 5 см, рассчитывается среднее значение прироста выходного параметра высоты растения за фазу, которое составляет 4.5 см. Для получения значения выходного параметра «Высота растения» необходимо сложить значение прироста параметра и значение выходного параметра предыдущей фазы, т.е. см. После чего происходит расчёт выходных параметров сле- дующей фазы. Для фазы «Развитие листьев» берутся значения входных параметров за период с 12 по 26 сентября. Аналогично по формулам 6-9 происходит расчёт выходного параметра для каждого входного параметра: для температуры воздуха это 6.4 см, для параметров содержание нитратов в почве, содержание фосфора в почве, содержание калия в почве это 5.7 см. Среднее значение прироста выходного параметра высоты растения за фазу равно 5.9 см. Высота растения за фазу развития листьев равна сумме высоты растения за фазу прорастания и среднего значения прироста и составляет 4.5 + 5.9 = 10.4 см.

5    Программное обеспечение цифровых двойников посевов растений

Описанный метод реализован в программном обеспечении, содержащем веб-интерфейс (см. рисунок 3), позволяющий задать входные данные (температура воздуха, запас питательной влаги, относительная влажность воздуха и др.) и представить результаты вычислений (масса растения, урожайность, количество листьев и др.). Для стадий развития представлена диаграмма их длительностей, где отмечено их сокращение или увеличение относительно базовых значений и другие особенности для лучшего понимания пользователем результатов.

Введите данные о фазах

Ввод даты начала 105.09.2023 О |

Ввод названия предыдущего растения | Озимая пшеница v |

| Рассчитать ] | Скачать Excel файл |

®е^вл=

Прорастание

Развитие листьев

Кущение (осеннее)

Кущение (весеннее)

Трубкование

Колошение

Цветение

Молочная спелость зе...

Восковая спелость зерна

Полная спелость зерна

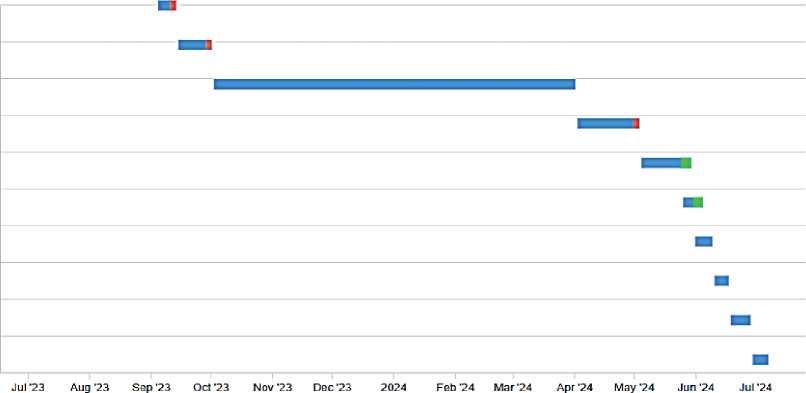
Рисунок 3 - Веб-интерфейс программы с диаграммой длительностей фаз

Для каждого входного параметра представляется график, где отображаются рекомендованные значения трубки, оптимальные и критические значения (см. пример на рисунке 4).

На рисунке 5 показана диаграмма основных классов системы. Класс «Модель» включает список фаз растения, каждая фаза состоит из номера, названия, списка выходных параметров и длительности фазы. Для каждого выходного параметра задаётся список входных параметров. На рисунке 5 классы, изображенные снизу, соответствуют структуре онтологии, которая загружается в систему в виде json файла. В одном json файле хранится модель растения одного сорта. Такая модель состоит из списка фаз роста и развития растения. Количество и названия фаз индивидуальны для каждого растения. Фазы состоят из выходных параметров. На каждый выходной параметр влияет входной параметр. Это влияние описано в трубках. Так как сорта растений отличаются друг от друга, то входные и выходные параметры задаются индивидуально.

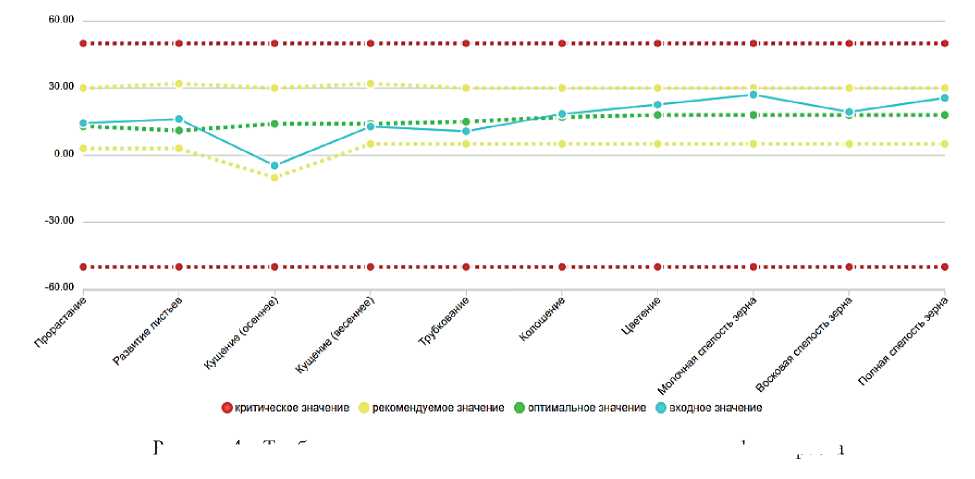
Рисунок 4 - Трубка входного параметра температуры воздуха по фазам роста

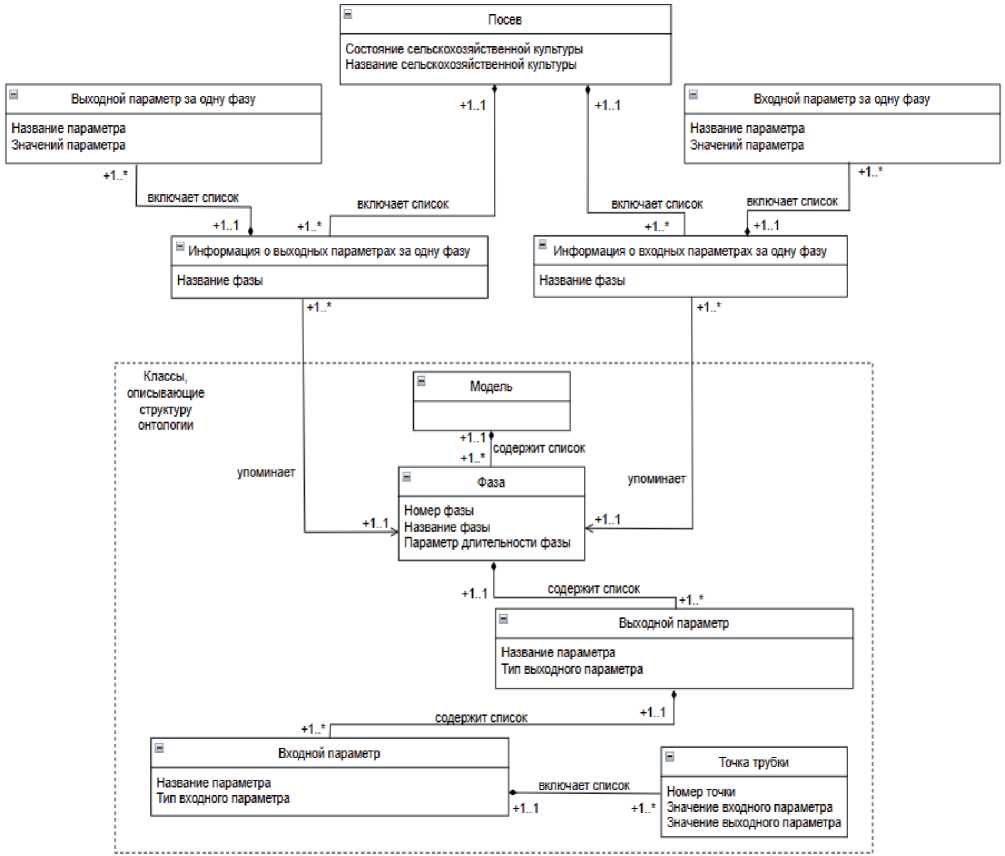
Рисунок 5 - Диаграмма основных классов системы

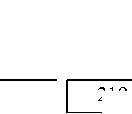
На рисунке 6 представлена структурная схема системы.

Рисунок 6 – Структурная схема системы

Разрабатываемая система состоит из следующих частей:

• ■    пользовательский интерфейс;

• ■    модуль преобразования данных, в состав которого входят сервисы предоставления данных: для пользовательского интерфейса; c пользовательского интерфейса для расчётов; модели из json файла;

• ■    модуль расчёта в виде сервисов: длительности фаз растения; выходных параметров растения.

Данные о фактическом и прогнозируемом состояниях погоды на тестовых полях на сезон были взяты из открытых источников . В экспериментах можно изменять прогноз погоды на сезон, микроэлементы в почве, влажность почвы и состав минералов. Устанавливая дату посева, пользователь запускает процесс вегетации в заданных условиях.

6 Результаты моделирования

Для оценки качества и эффективности ЦДПР разработана методика, включающая два этапа:

• 1 ) Качественная проверка: проверка на здравый смысл, когда изменяются входные параметры среды и погоды по событиям – измеряется результат, т.е. план роста и развития посевов растений и прогноз урожайности, который должен в целом соответствовать требованиям, заложенным селекционерами в сорт.

• 2 ) Количественная проверка: сопоставление стадий роста и развития виртуальных и реальных посевов растений, начиная со дня высева.

• 6 .1 Результаты моделирования погодных событий и внесения удобрений

Для моделирования использовались трубки входных параметров для культуры «Озимая пшеница», полученные из лаборатории Цифровые двойники растений СамНЦ РАН.

В качестве выходного параметра рассмотрена высота растения.

На основе созданного прототипа ЦДПР проведены эксперименты по моделированию событий жара-холод, засуха-дожди, внесение удобрений. В таблице 1 представлены трубки влияющих факторов для фазы «Прорастание».

Пример графиков для граничных значений трубки фактора «Температура воздуха» и входного значения фактора на каждой фазе при благоприятных условиях приведены на рисунке 7.

Таблица 1 – Трубки входных параметров для фазы «Прорастание»

Название входного параметра	Название точек трубки	Значение входного параметра	Значение дельты выходного параметра высоты растения
Т воздуха, оС	Критический минимум	30	5
	Оптимальное значение	13	6
	Критический максимум	3	3
Запасы нитратов в слое, 0 –30 см, мг/кг	Критический минимум	200	5
	Оптимальное значение	20	6
	Критический максимум	3	4
Запасы оксида фосфора в слое, 0 – 30 см, мг/кг	Критический минимум	800	5
	Оптимальное значение	200	6
	Критический максимум	20	4
Запасы оксида калия в слое, 0 – 30 см, мг/кг	Критический минимум	800	5
	Оптимальное значение	180	6
	Критический максимум	20	4

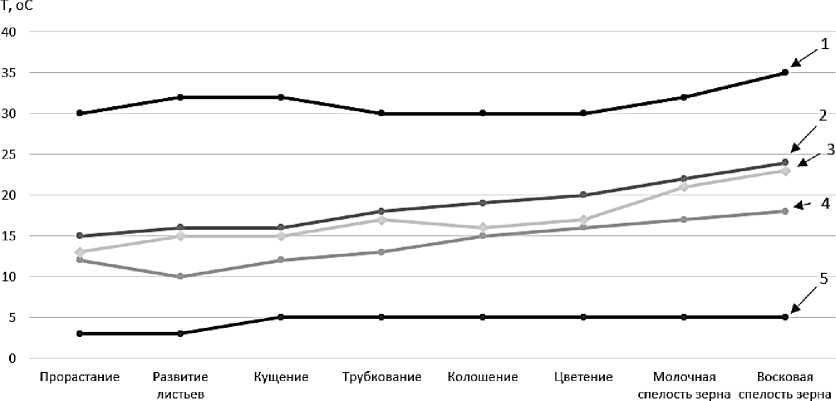
Фаза роста

1 – критический максимум, 2 – рекомендуемый максимум, 3 – входное значение фактора, 4 – рекомендуемый минимум, 5 – критический минимум

Рисунок 7 – Пример графиков температуры воздуха на каждой фазе при благоприятных условиях

На рисунке 8 приведены результаты экспериментов с различными сценариями:

• ■    благоприятные условия произрастания - входные данные для каждой фазы развития взяты с полей с/х культуры «Озимая пшеница» Безенчукского района Самарской области;

• ■    перенасыщение питательными веществами - смоделирована избыточность влаги в почве на ранних фазах развития растения;

• ■    условия засухи - смоделирована низкая влажность на ранних фазах развития растения;

• ■    недостаток питательных веществ - смоделирован недостаток азота в почве на ранних фазах развития растения.

На последней стадии норма параметра высоты растения составляет 100 см.

Как видно из рисунка 7, при сценарии благоприятных условий фактор «Температура воздуха» на всех стадиях колебался в границах рекомендуемых минимума и максимума, остальные влияющие факторы так же оставались в рамках рекомендуемых значений на всех фазах роста, из-за чего прогнозируемое значение высоты растения (рисунок 8, график 2) близко к норме, разница в росте составила 1.57 см.

Для сценария перенасыщения питательными веществами на стадии кущения оптимальное и итоговое значения высоты растения (рисунок 8, график 3) значительно разошлись из-за избытка питательных веществ. В результате в конце развития растения разница в росте составила 10.43 см.

о

Прорастание Развитие листьев         Кущение           Трубкование          Колошение            Цветение Молочная спелость Восковая спелость зерна                зерна

Фаза роста

1 – норма высоты растения, 2 – результат эксперимента сценария благоприятных условий, 3 – результат эксперимента сценария перенасыщения питательными веществами, 4 – результат эксперимента сценария засухи, 5 – результат эксперимента сценария недостатка питательных веществ

Рисунок 8 – Пример графика параметра высоты растения с различными сценариями

Расхождение на стадии кущения также наблюдается и для сценария засухи из-за низкой влажности (рисунок 8, график 4). В результате в конце развития растения разница в росте составила 24.04 см.

Для сценария недостатка питательных веществ разница между оптимальным и итоговым значением высоты в конце развития растения составила 23.46 см (рисунок 8, график 5).

• 6 .2 Результаты сравнения фактических и рассчитанных значений

  Проведено сравнение фактических дат начала и конца фаз с/х культуры c рассчитанными значениями (рисунок 9). Из рисунка видно, что разница между значениями фактических и рассчитанных дат не превышает 14 дней. Дата фактического сбора урожая была 16.07.2024, а дата рассчитанного сбора – 28.07.2024.

На рисунке 10 представлено сравнение значений по количествам дней в фазе.

Проведено сравнение фактической высоты растения и рассчитанных значений (рисунок 11). Для оценки правильности расчётов взята модель ЦД растения из [9].

Фактическая высота растения на момент сбора урожая составила 110 см, значение, полученное с помощью модели ЦД растения, – 99.88 см, значение, полученное с помощью предложенного метода, – 96.38 см. Полученное отклонение от фактического значения связано с тем, что в используемой модели ожидаемая высота растения ограничивалась 100 см. В действительности растение выросло до 110 см, что подтверждает сложность моделирования процесса развития растения, зависящего от многих факторов.

Проведённые исследования показали, что разработанная модель адекватно реагирует на важные события и соответствует натурным данным, что позволяет считать её пригодной для практического применения агрономами и дальнейшего развития.

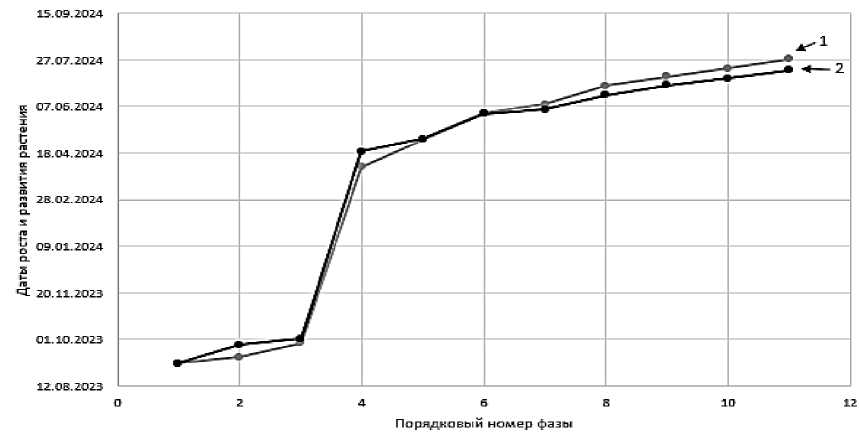
1 – рассчитанные значения, 2 – фактические значения

Рисунок 9 – Сравнение фактических и рассчитанных значений дат начала и конца фаз

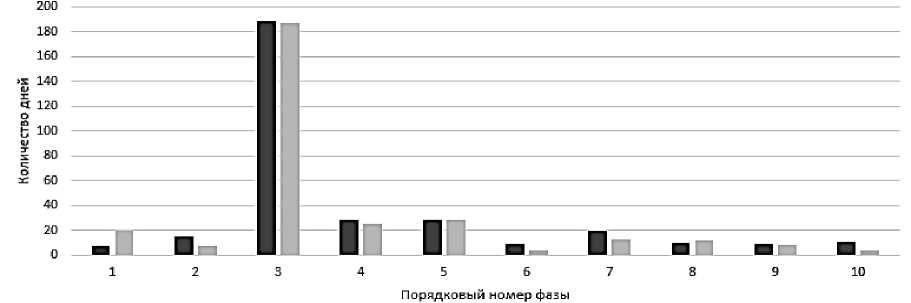
слева – рассчитанные значения, справа – фактические значения

Рисунок 10 – Сравнение количества фактических и рассчитанных дней длительности фаз

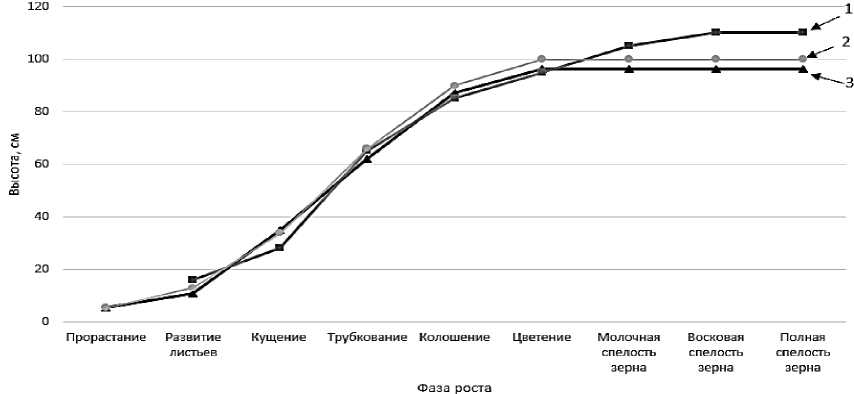
1 – фактические значения, 2 – значения, рассчитанные моделью ЦД растений, 3 – значения, рассчитанные предложенным методом

Рисунок 11 – Сравнение фактических и рассчитанных значений высоты растения

Заключение

В работе предложен метод расчёта параметров состояний растений, который может дополнять методы, основанные на нейронных сетях, и другие подходы.

В разработанном методе использует понятие трубки – диапазонов оптимальных и критических для выживания растений значений основных факторов, которые характеризуют фазы роста и развития растения и влияние входных параметров каждого интервала на выходные параметры растения. Результаты моделирования на примере культуры «Озимая пшеница» и сравнение процессов роста и развития виртуальных и реальных посевов показывают применимость такого подхода для моделирования процесса развития растений.

Дальнейшие исследования целесообразно направить на развитие и совершенствование метода расчёта стадий и прогнозирование урожая, включая построение более глубоких онтологий для интеграции знаний о предметной области и мультиагентных технологий для адаптивного планирования развития посевов растений с учётом любых событий.

В результате может быть создана практичная интеллектуальная система моделирования и прогнозирования стадий роста и развития разных сортов с/x культур и их урожайности.