Прогнозирование ремонтопригодности лесозаготовительных машин

ПОСТАНОВКА ПРОБЛЕМЫ

В ходе проектирования лесозаготовительной машины (ЛЗМ) перед конструктором периодически возникает задача оценки ремонтопригодности создаваемой конструкции с целью убедиться в обоснованности принятых решений.

Задача качественной оценки уровня ремонтопригодности машины на стадиях проектирования решается, в основном, такими методами, как метод сравнения с прототипом и экспертным методом [1], в том числе, методом оценки по баллам при отсутствии явно выраженного прототипа.

Количественные методы задания и оценки ремонтопригодности позволяют создать и использовать методы прогнозирования показателей ремонтопригодности, основанные на использовании методов и аппарата математической статистики и, в первую очередь, методов корреляции, многофакторного и регрессионного анализа [2]. Границы применения того или иного метода определяются многими факторами, в том числе, степенью конструктивной преемственности машин и однородностью условий их обслуживания и ремонта. Поэтому прогноз показателя может быть корректным, если значения конструктивных параметров оцениваемого элемента, подставляемые в уравнение, находятся в пределах матрицы наблюдений, на основе которой получено уравнение связи или регрессии.

Конкретной задачей прогнозирования является предсказание количественной величины показателя ремонтопригодности проектируемого объекта.

МЕТОДИКА И ОБЪЕКТЫ ИССЛЕДОВАНИЯ

В качестве примера определим уравнение связи между величиной времени восстановления работоспособности лесозаготовительной машины и весом ЛЗМ.

Рассмотрим количественные характеристики ремонтопригодности тракторов «ОТЗ» [ТДТ-55А; ТБ-1М (ТБ-1М-15)] и лесозаготовительных машин на базе (ЛП-30Г; ПЛ-1В; ЛП-17А).

Одним из основных количественных показателей ремонтопригодности ЛЗМ является их среднее время восстановления или среднее время устранения среднестатистического отказа. Одной из основных систем, время устранения отказа которой в наибольшей степени зависит от агрегатированности, то есть насыщения технологическим оборудованием и гидросистемой, является трансмиссия ЛЗМ. Наличие более сложного технологического оборудования и гидросистемы определяет увеличение веса ЛЗМ как по сравнению с базовой моделью, так и по сравнению с ее аналогами и прототипами.

В таблице 1 представлены данные опытных наблюдений за тракторами «ОТЗ» и ЛЗМ на их базе за наработку в объеме 3000 моточасов в условиях опорных пунктов КарНИИЛПа [3], то есть лесозаготовительных предприятий Республики Карелия.

Для определения уравнения связи (корреляции) между весом ЛЗМ ( х ) и средним временем восстановления, то есть устранения среднестатистического отказа трансмиссии ( у ), согласно рекомендациям работы [4], составим расчетную вспомогательную таблицу 2, предполагая, согласно рисунку 1, непрямолинейность характера искомого уравнения связи, уравнения параболы вида: y = ax² + bx + c.

По результатам вспомогательных расчетов составляем ориентировочную таблицу 3. В заголовках первых трех столбцов и всех строчек таблицы записывают те выражения, которые в принятом уравнении параболы являются множителями при параметрах a, b, c, то есть х2 – при параметре а, х – при параметре b и 1 – при параметре с. В заголовке последнего столбца ставится определяемая по этому уравнению величина у. Затем в каждой клетке этой таблицы записываются произведения двух соответствующих заголовков. Например, на пересечении второго столбца (с заголовком х) и первой строчки (с заголовком х2) следует записать произведение этих заголовков х3. Если не принимать во внимание повторения, то в таблице имеется восемь разных выражений (х4, х3, х2, х, х2у, ху, у и 1). В окончательной ориентировочной таблице вместо 1 записано 5. Это сделано на том основании, что во всех клетках записывают суммы числовых значений соответствующих выражений. Единицу нужно было повторять пять раз, то есть получилось бы число 5, что и записано в таблицу. Вместо едини- цы в ориентировочной таблице записывается общее число наблюдений.

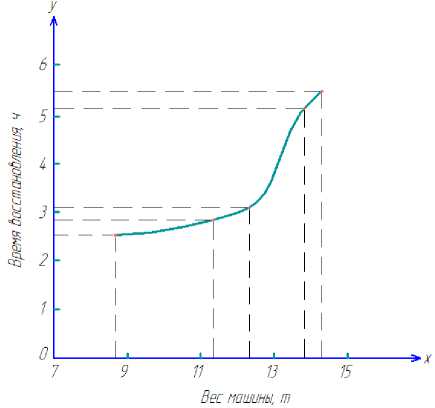
Рис. 1. Эмпирическая зависимость времени восстановления от веса машины

С помощью окончательной ориентировочной таблицы составляются так называемые «нормальные» уравнения, при совместном решении которых можно определить числовые значения параметров a , b , c . Первое уравнение получаем из чисел первой строчки, второе – из чисел второй и третье – из чисел третьей, причем первые три числа каждой строчки служат коэффициентами при параметрах a , b , c , а последние числа являются свободными членами уравнения.

Итак, получаем систему трех, так называемых «нормальных», уравнений с тремя неизвестными значениями параметров a , b , c :

123005,99a + 9514,61 b + 749,60c = = 3130,75;

9514,61 a + 749,60b + 60,40c = 241,93 ;749,60a + 60,40b + 5,00 c = 19,10.

Систему уравнений с целью определения количественных значений параметров решаем способом сложения и вычитания. Первоначально каждое уравнение соответственно делят на коэффициент при c и получают новую систему уравнений с коэффициентом 1 при c . Затем для исключения параметра c вычитают второе уравнение из первого и третье из второго. Из оставшихся двух уравнений с двумя неизвестными a и b таким же способом исключают параметр b и находят значение параметра а . Подставив значение параметра a в одно из уравнений с двумя неизвестными, определим значение параметра b . Затем, подставив значения параметров a и b в одно из уравнений с тремя неизвестными, находим значение параметра c . В нашем случае параметры a , b и c равны:

a = 0,075; b = -1,15; c = 6,49. Правильность вычислений параметров проверим путем подстановки их в одно из первоначальных уравнений.

Проверка:

749,60 • 0,075 + 60,40 •(-1,15)+5 • 6,49 = = 19,06 «19,10.

Вычисления сделаны правильно. Разница в 0,04 обусловлена округлением при вычислениях.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙИ ОСНОВНЫЕ ВЫВОДЫ

Подставив полученные значения параметров в уравнение параболы y = ax2 + bx + c, получаем: y = 0,075x2 – 1,15x + 6,49. Пригодность полученного уравнения оценим путем сравнения экспериментальных данных с данными, вычисленными по этому уравнению. Результаты расчетных и экспериментальных данных представлены в таблице 4.

Наименьшая сумма квадратов отклонений (Δ2) принятого уравнения равна 0,35.

Данное уравнение допустимо для практического использования, хотя не исключаются и более точные результаты при использовании другой формулы, например типа у = ахb.

Учитывая, что область применения уравнения может быть расширена до 20 % от исследуемых предельных величин параметра, то есть веса ЛЗМ, его можно применять в диапазоне изменения веса проектируемой машины от 7,0 до 17,0 тонн.

Итак, по результатам исследований можно сформулировать следующие выводы:

• 1.    Прогнозирование количественных значений показателей ремонтопригодности как показателя качества перспективных лесозаготовительных машин может быть осуществлено с использованием обыкновенных корреляционных уравнений, основывающихся на статистических результатах испытаний на надежность аналогов и прототипов ЛЗМ.

• 2.    Корреляционное уравнение связи между весом машины и величиной времени восстановления работоспособного состояния трансмиссии для тракторов «ОТЗ» и лесозаготовительных машин на их базе может представлять собой уравнение параболы вида у = 0,075х² – 1,15х + 6,49.